Eigenschappen van een strak gefocuste circulair gepolariseerde afwijkende vortexstraal en zijn optische krachten op gevangen nanodeeltjes

Abstract

De kenmerken van een circulair gepolariseerde afwijkende vortexbundel (CPAVB), gefocusseerd door een objectieflens met een hoge numerieke apertuur (NA), worden analytisch en theoretisch bestudeerd. Het laat zien dat de topologische lading het straalprofiel aanzienlijk kan beïnvloeden en dat een afgeplatte (FT) straal kan worden verkregen door de NA en topologische lading te moduleren. Het is interessant om te ontdekken dat conversie van spin-naar-orbitaal impulsmoment kan plaatsvinden in de longitudinale component na scherp scherpstellen. Verder worden de optische krachten van het strak gefocuste CPAVB op nanodeeltjes in detail geanalyseerd. Het kan worden verwacht dat twee soorten nanodeeltjes worden opgevangen met behulp van een dergelijke straal in de buurt van de focus.

Inleiding

Vortexbundels met een spiraalfasefactor exp(imθ ) hebben de afgelopen twee decennia veel aandacht getrokken, waar m is een topologische lading en kan elk geheel getal zijn en θ is de azimuthoek op een vlak dwars op de optische as [1, 2]. Vortex-bundels zijn op grote schaal gebruikt in tal van toepassingen vanwege hun "donut"-intensiteitsprofiel en orbitaal impulsmoment (OAM), zoals optische pincetten [3,4,5,6,7], optische communicatie in de vrije ruimte [8], en kwantuminformatie [9]. Onlangs hebben onderzoekers meer aandacht besteed aan de studie van circulair gepolariseerde vortexbundel vanwege zijn unieke kenmerken [10,11,12,13,14,15], het draagt bijvoorbeeld zowel spin-impulsmomentum (SAM) als OAM aan de dezelfde tijd. Deze unieke eigenschappen kunnen de toepassingen van wervelstralen aanzienlijk uitbreiden en verbeteren.

De sterk focusserende eigenschappen van verschillende bundels onder een lenssysteem met een hoge NA is een ander hot topic [16,17,18,19,20] vanwege hun belangrijke toepassingen in het vangen van deeltjes [21], microscopie [22], optische gegevensopslag [23 ], enz. Tot dusver zijn verschillende bundels bestudeerd, variërend van scalaire vortex-bundels tot vector vortex-bundels [10, 24,25,26,27,28,29,30,31]. Hao et al. [26] en Pu et al. [27] bestudeerde de eigenschappen van een spiraalgepolariseerde vortexbundel onder een hoge NA-lens. Er werd aangetoond dat een flat-topped (FT) profiel kan worden bereikt en dat de OAM kan worden aangepast door een juiste gepolariseerde toestand in het brandvlak te kiezen. Zhan et al. bestudeerde de eigenschappen van strak gefocuste vortexbundels met circulair polarisatie [10], wat aantoont dat een sterke longitudinale component kan worden geproduceerd.

Een afwijkende vortexstraal (AVB), een nieuwe straal die kan evolueren tot een elegante Laguerre-Gaussiaanse straal in het verre veld, werd onlangs voorgesteld [32]. Een dergelijke bundel heeft veel aandacht getrokken en is uitgebreid onderzocht [33,34,35,36,37,38] vanwege zijn buitengewone voortplantingseigenschappen. Voor zover wij weten, is er geen rapport over de CPAVB's die zijn gefocust door een lens met een hoge NA. In dit artikel worden de wiskundige uitdrukkingen van de CPAVB's na strakke focus afgeleid. Vervolgens analyseren we het effect van bundelvolgorde, topologische lading en NA-waarde op het bundelprofiel en de faseverdeling. In het laatste deel worden optische krachten van strak gefocuste CPAVB's bestudeerd.

Methoden

Een circulair gepolariseerde bundel kan als volgt worden geschreven, wat de lineaire superpositie van radiaal en azimutaal gepolariseerde bundels aangeeft [10]:

$$ {\mathrm{E}}_{LHC(RHC)}=P(r){e}^{\pm i\varphi}\left({\mathrm{e}}_{\rho}\pm j {\mathrm{e}}_{\varphi}\right)/\sqrt{2} $$ (1)

waar P (r ) is de amplitudeverdeling. Het teken "+" en "−" zijn respectievelijk linker en rechter circulaire polarisatie. e _ρ en e _φ zijn respectievelijk de radiale en azimutale vectoren in de cilindrische coördinaten. En uitdrukkingen van de radiaal en azimutaal gepolariseerde bundel kunnen worden verkregen in [39,40,41].

Het schema van het focussysteem is hetzelfde als Ref. [42]. De pupilapodisatiefunctie van AVB onder een sinusconditie (d.w.z. r = f sinθ ) kan worden geschreven als [32, 38]:

$$ {\mathrm{E}}_{\mathrm{n},\mathrm{m}}\left(\theta, \varphi \right)={E}_0{\left(\frac{f\sin \ theta }{w_0}\right)}^{2n+\left|m\right|}\exp \left(-\frac{f^2{\sin}^2\theta }{{w_0}^2}\right )\exp \left(- im\varphi \right) $$ (2)

waar f is de brandpuntsafstand, θ varieert van 0 tot α , α is de maximale hoek van NA, en E ₀ en w ₀ zijn respectievelijk een constante en tailleradius. n , φ , en m zijn respectievelijk de bundelvolgorde, azimutale coördinaten en de topologische lading.

Volgens de vector Debye-theorie kunnen de uitdrukkingen van het elektrische veld, van de strak gefocuste CPAVB in cilindrische coördinaten, worden afgeleid als Vgl. (3):

$$ {\displaystyle \begin{array}{l}{E}_{\pm, \rho}\left(\rho, \varphi, z\right)=-\frac{ikf}{2}{\int }_0^{\alpha }{E}_0{\left(\frac{f\sin \theta }{w_0}\right)}^{2n+\left|m\right|}\exp \left(-\frac {f^2{\sin}^2\theta }{w_0}\right){i}^m\\ {}\kern6.399996em \times \sin \theta \sqrt{\cos \theta}\exp \left ( ikz\cos \theta \right)\exp \left[i\left(m\pm 1\right)\varphi \right]\\ {}\kern6.399996em \times \left[\left(\cos \theta +1\right){J}_m\left( k\rho \sin \theta \right)-\left(\cos \theta -1\right){J}_{m\pm 2}\left( k\ rho \sin \theta \right)\right] d\theta \end{array}} $$ (3a) $$ {\displaystyle \begin{array}{l}{E}_{\pm, \varphi}\ left(\rho, \varphi, z\right)=-\frac{ikf}{2}{\int}_0^{\alpha }{E}_0{\left(\frac{f\sin \theta }{ w_0}\right)}^{2n+\left|m\right|}\exp \left(-\frac{f^2{\sin}^2\theta }{w_0}\right){i}^{m \pm 1}\\ {}\kern6.399996em \times \sin \theta \sqrt{\cos \theta}\exp \left( ikz\cos \theta \right)\exp \left[i\left(m\ pm 1\right)\varphi \right]\\ {}\kern6.399996em \times \left[\left(\cos \t heta +1\right){J}_m\left( k\rho \sin \theta \right)-\left(\cos \theta -1\right){J}_{m\pm 2}\left( k \rho \sin \theta \right)\right] d\theta \end{array}} $$ (3b) $$ {\displaystyle \begin{array}{l}{E}_{\pm, z}\ left(\rho, \varphi, z\right)=- ikf{\int}_0^{\alpha }{E}_0{\left(\frac{f\sin \theta }{w_0}\right)}^ {2n+\left|m\right|}\exp \left(-\frac{f^2{\sin}^2\theta }{w_0}\right){i}^{m\pm 1}\\ { }\kern6.399996em \times {\sin}^2\theta \sqrt{\cos \theta}\exp \left( ikz\cos \theta \right)\exp \left[i\left(m\pm 1\ rechts)\varphi \right]\\ {}\kern6.399996em \times {J}_{m\pm 1}\left( k\rho \sin \theta \right) d\theta \end{array}} $ $ (3c)

waar J _n (α ) is een n -orde Bessel-functie van de eerste soort en k = 2π/λ. We definiëren E ₊ en E ₋ als de uitdrukking van het elektrische veld van respectievelijk de rechter en linker CPAVB.

In de bovenstaande vergelijkingen worden de volgende formules gebruikt [43]:

$$ \left\{\begin{array}{l}{\int}_0^{2\pi}\cos \left( n\varphi \right)\exp \left[ ia\cos \left(\varphi - \phi \right)\right] d\varphi =2\pi {i}^n{J}_n(a)\cos \left( n\phi \right)\\ {}{\int}_0^{2 \pi}\sin \left( n\varphi \right)\exp \left[ ia\cos \left(\varphi -\phi \right)\right] d\varphi =2\pi {i}^n{J }_n(a)\sin \left( n\phi \right)\end{array}\right. $$ (4)

Vervolgens kunnen we de totale intensiteit van de strak gefocuste CPAVB als volgt berekenen:

$$ I={\left|{E}_{\rho}\left(\rho, \varphi, z\right)\right|}^2+{\left|{E}_{\varphi}\left (\rho, \varphi, z\right)\right|}^2+{\left|{E}_z\left(\rho, \varphi, z\right)\right|}^2 $$ (5)

waar E _ρ , E _φ , en E _z zijn de amplitudes van corresponderende componenten.

Resultaten en discussie

Strakke focuskenmerken van de CPAVB

In deze sectie bestuderen we met behulp van de bovenstaande vergelijkingen de eigenschappen van de strak gefocuste CPAVB. In de simulatie stellen we NA = 0,85, λ = 632.8 nm, w ₀ = 2 mm, en f = 2 mm. In Fig. 1 het totale intensiteitsprofiel en bijbehorende longitudinale en radiale componenten van de linker CPAVB's met n =1 voor verschillende topologische ladingen in het brandvlak worden respectievelijk afgebeeld. We kunnen zien dat de totale intensiteit in het midden niet nul is wanneer m ≤ 2, terwijl er een donkere vlek in het midden is wanneer m> 2 Bovendien is de radiale component van gefocusseerde velden niet nul op de as wanneer m = 0, 2, en hetzelfde als de longitudinale component wanneer m =1. Deze resultaten kunnen worden verklaard uit Vgl. (3) en vgl. (5), vanwege het feit dat J _m is altijd gelijk aan nul in de oorsprong behalve m = 0. De Bessel-functie van de eerste soort in alle drie de componenten is nul in het midden wanneer m> 2, en dus is de totale intensiteit nul. Anders bestaat er minstens één component met J ₀ , wat betekent dat de centrale intensiteit niet nul en maximaal kan zijn. Bovendien neemt voor totale en radiale componenten de grootte van het brandpunt toe naarmate de topologische lading toeneemt. Daarom kunnen we concluderen dat de totale intensiteit en brandpuntgrootte in het brandpuntsveld worden beïnvloed door topologische lading.

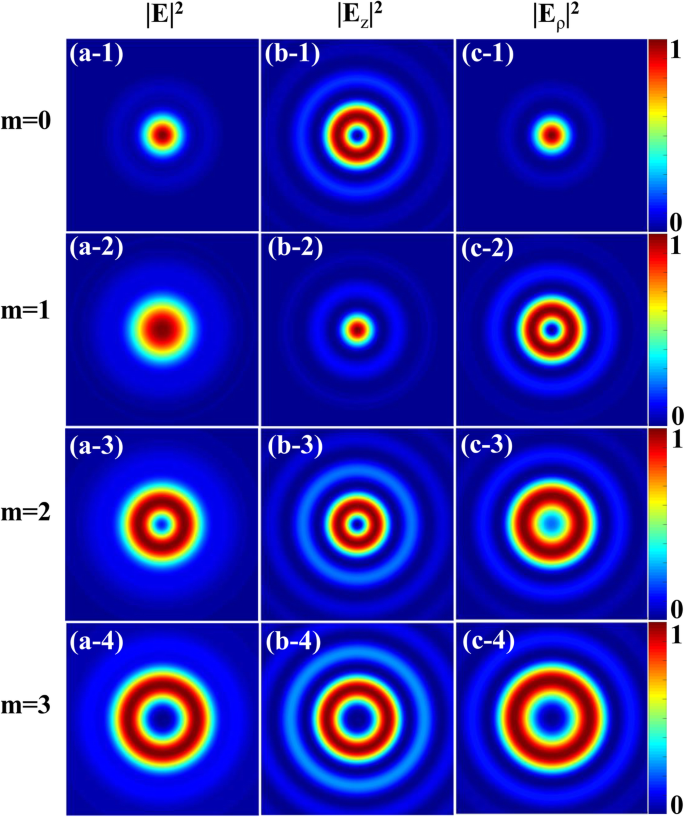
Intensiteitsprofiel voor de strak gefocuste linker CPAVB's met n =1 voor verschillende topologische ladingen. a-1 tot a-4 , b-1 tot b-4 , en c-1 naar c-3 zijn de totale intensiteit |E |² en longitudinaal |E _z |² en radiaal |E _ρ |² componenten, respectievelijk

In Fig. 2, het totale intensiteitsprofiel en bijbehorende longitudinale en radiale componenten van de linker CPAVB's met m =1 voor verschillende bundelorden in het brandvlak zijn respectievelijk afgebeeld. Je kunt dat zien als n neemt toe, worden de buitenste ringen van elk onderdeel en de totale intensiteit geleidelijk helderder, terwijl het patroon van de intensiteit niet verandert. Dus de bundelvolgorde n heeft geen grote invloed op de vorm van de intensiteitspatronen.

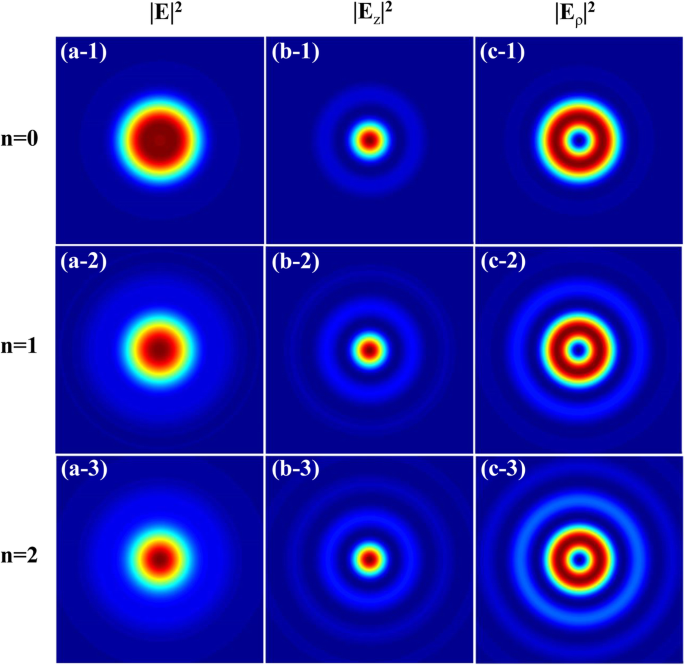
Intensiteitsprofiel voor de strak gefocuste linker CPAVB's met m = 1 voor verschillende straalorders. a-1 tot a-3 , b-1 naar b-3 , en c-1 naar c-3 zijn de totale intensiteit |E |² en longitudinaal |E _z |² en radiaal |E _ρ |² componenten, respectievelijk

Vervolgens bestuderen we hoe de NA-waarde de focusseringseigenschappen van CPAVB's beïnvloedt met n = 2 voor m = 1 en m =4, respectievelijk. Zoals getoond in Fig. 3, is het merkbaar dat de centrale intensiteit niet nul blijft in het geval van topologische lading m = 1, terwijl de centrale intensiteit m . donker is in het brandvlak =4. Als we figuur 3 d-1 vergelijken met d-2, kunnen we zien dat de intensiteit toeneemt en zich naar het centrum verzamelt met toenemende NA. Vooral in het geval van m =-1, een FT-straal kan worden verkregen wanneer NA toeneemt tot 0,8.

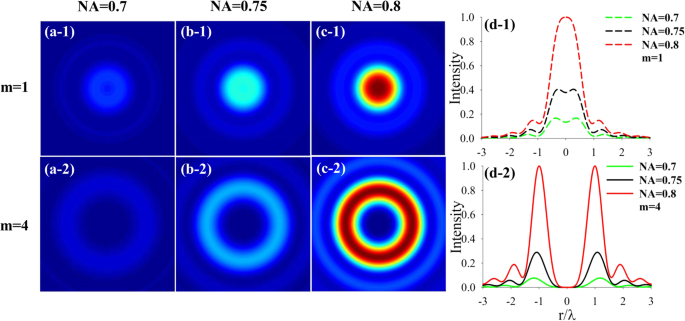
Variatie van de intensiteit met de verschillende NA van de linker CPAVB's met m = 1 en m =4, respectievelijk. a-1 en a-2 , b-1 en b-2 , en c-1 en c-2 zijn respectievelijk NA = 0,7, 0,75, 0,8. d-1 en d-2 Doorsnede van de intensiteit

Gebaseerd op vgl. (3c), berekenden we de faseverdelingen van longitudinale component-CPAVB's in de buurt van focus, zoals weergegeven in figuur 4. De eerste en tweede rij van figuur 4 zijn respectievelijk de linker en rechter CPAVB's. De locatie voor Fig. 4 a–c is z = − 0.005z _r , 0, 0.005z _r , respectievelijk, waar z _r = kw ₀ ² /2 is het Rayleigh-assortiment. Andere parameters zijn ingesteld als n = 1 en NA = 0,85. Zoals getoond in Fig. 4, verandert de contour van fasepatronen van met de klok mee naar tegen de klok in nadat ze door het brandpuntsvlak zijn gegaan. Als we Fig. 4 a-1 met c-1 vergelijken met Fig. 4 a-2 tot c-2, is het interessant om te zien dat de topologische lading nabij het brandpunt verandert van 3 naar 5 wanneer de linker CPAVB wordt vervangen door een rechtse. Dit fenomeen kan worden verklaard als een linker CPAVB met m = 4 draagt SAM l _s = −ħ en OAM m = 4ħ . Door de compensatie van de tegenovergestelde OAM omgezet van SAM, nemen de topologische ladingen af tot drie na scherp scherpstellen. Naar analogie kunnen we hetzelfde gedrag verwachten van de rechterhand CPAVB met m = 4, die SAM l . draagt _s =ħ en OAM m = 4ħ . Doordat OAM is omgezet van SAM, nemen de topologische ladingen toe tot vijf. Daarom kunnen we concluderen dat er een conversie is van SAM naar OAM in de longitudinale component na scherp scherpstellen.

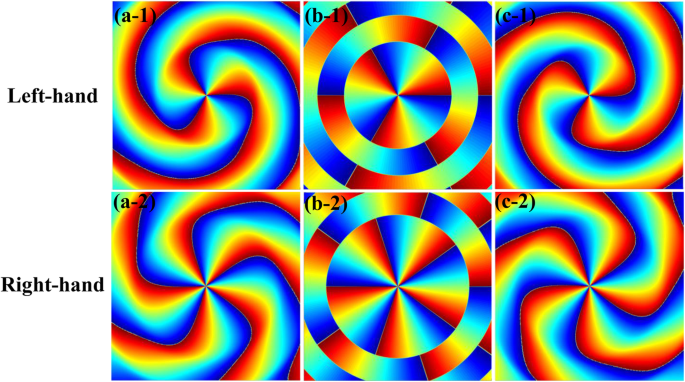
Faseprofiel van de longitudinale component van CPAVB's met m = 4 dichtbij het brandpunt. De eerste en tweede rij zijn respectievelijk de linker en rechter CPAVB's. a-1 naar a-2 z = − 0.005z _r . b-1 naar b-2 z = 0. c-1 naar c-2 z = 0.005z _r

Nanodeeltjes vangen met behulp van de nauw gerichte CPAVB

Op basis van de Rayleigh-verstrooiingstheorie [44] moeten de verstrooiingskracht en gradiëntkracht worden overwogen bij de bespreking van de optische trapping. De verstrooiingskracht, geschreven als F _scat = e _z n _m αIk _uit /c , heeft de neiging om de optische val te destabiliseren, waarbij c is lichtsnelheid, e _z is een eenheidsvector langs de z richting, ik _uit is de intensiteit van de gefocusseerde straal, α = (8/3)π (ka )⁴ een ² [(η ² − 1)² /(η ² + 2)² ], ɑ is de straal van het nanodeeltje, η = n _p /n _m , en n _m en n _p zijn respectievelijk de brekingsindex van omringende media en nanodeeltjes. En de gradiëntkracht (F _afstudeerder ) trends om een nanodeeltje terug naar de focus te trekken, wat kan worden uitgedrukt als F_grad = 2πn _m β ∇ Ik _uit /c , waar β = een ³ (η ² − 1)/(η ² + 2).

In het simulatie-experiment stellen we n _p = 1.59 en n _p = 1 voor respectievelijk glas en luchtbel, n _m = 1.332, NA = 0.85, en ɑ = 50 nm. Figuur 5 geeft de radiale, longitudinale gradiëntkrachten en verstrooiingskrachten weer van een linker CPAVB op een nanodeeltje met n _p = 1 voor verschillende m en n . Het vorige werk laat zien dat de totale intensiteit in het midden donker is wanneer m ≥ 3. Daarom zullen, zoals verwacht, voor nanodeeltjes met een lage brekingsindex de radiale en longitudinale gradiëntkracht het nanodeeltje altijd terugtrekken naar de focus, zoals weergegeven in figuur 5 a-d. In vergelijking met de gradiëntkracht is de verstrooiingskracht erg klein. Daarom kan het nanodeeltje met lage brekingsindex stabiel worden opgesloten.

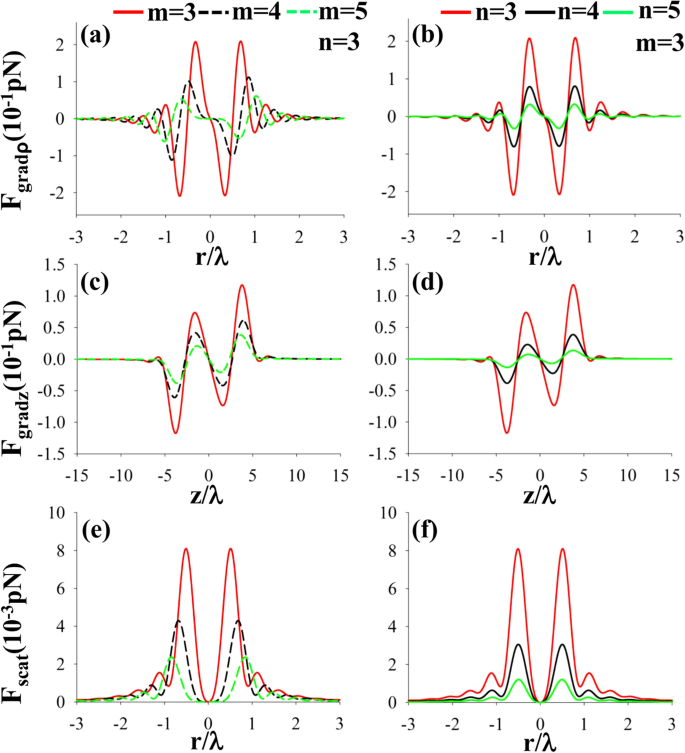
een –f De radiale, longitudinale gradiëntkrachten en verstrooiingskrachten van een linker CPAVB na scherpe focus op een deeltje met lage brekingsindex n _p = 1

Figuur 6 geeft de radiale, longitudinale gradiëntkrachten en verstrooiingskrachten weer van een linker CPAVB op een nanodeeltje met n _p = 1.59 voor verschillende topologische ladingen m en de straal orders n . Uit Fig. 6 kunnen we zien dat er verschillende evenwichtspunten in de buurt van het brandpunt zijn en dat de verstrooiingskracht kan worden verwaarloosd in vergelijking met de gradiëntkracht. Daarom kan het nanodeeltje met hoge brekingsindex dichtbij de focus worden vastgelegd.

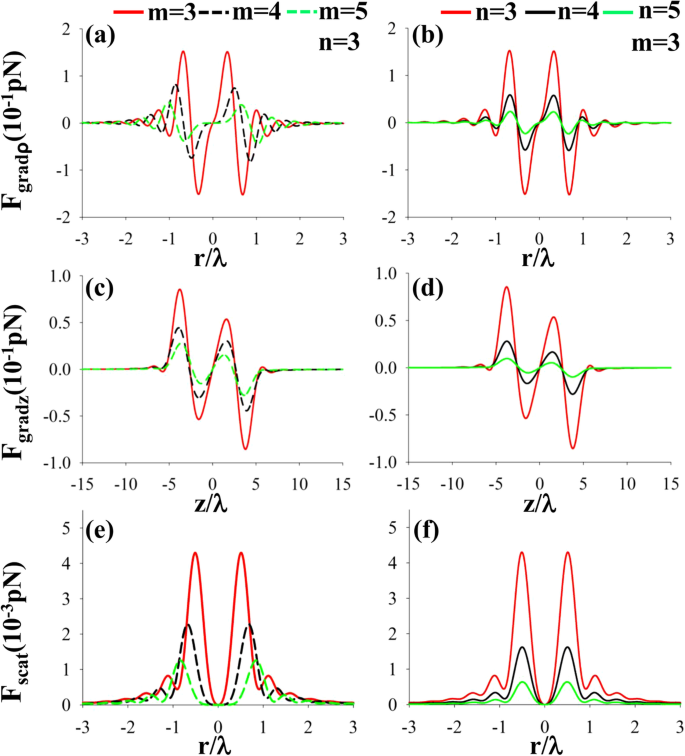
een –f De radiale, longitudinale gradiëntkrachten en verstrooiingskrachten van een linker CPAVB na scherpe focus op een deeltje met hoge brekingsindex n _p = 1.59

Conclusies

In dit artikel zijn de kenmerken van strak gefocuste CPAVB's en hun optische krachten op nanodeeltjes besproken. We vinden dat SAM van CPAVB kan worden omgezet in OAM wanneer een dergelijke straal strak is gefocust. Bovendien kan strak gefocusseerde CPAVB worden gebruikt om twee verschillende soorten nanodeeltjes, met een lage en hoge brekingsindex, in de buurt van het brandpuntsvlak te vangen. Ons onderzoek zal helpen bij het vinden van mogelijke toepassingen van CPAVB.

Beschikbaarheid van gegevens en materialen

De datasets die tijdens het huidige onderzoek zijn gegenereerd en/of geanalyseerd, zijn op redelijk verzoek verkrijgbaar bij de corresponderende auteur.

Afkortingen

AVB:: Afwijkende vortexstraal
CPAVB:: Circulair gepolariseerde afwijkende vortexstraal
FT:: Platte bovenkant
NA:: Numeriek diafragma
OAM:: Orbitaal impulsmoment
SAM:: Draaiimpulsmoment

Controle van contactconfiguratie van op carbonzuur gebaseerde moleculaire verbindingen via zijgroep Elektrospun polytetrafluorethyleen nanovezelmembraan voor hoogwaardige, zelfaangedreven sensoren

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal