Morfologische evolutie van Si(001)-substraten met pitpatroon aangedreven door reductie van oppervlakte-energie

Abstract

Laterale ordening van hetero-epitaxiale eilanden kan gemakkelijk worden bereikt door geschikte putpatroonvorming van het substraat voorafgaand aan afzetting. Het regelen van de vorm, oriëntatie en grootte van de pits is niet triviaal, aangezien ze metastabiel zijn en aanzienlijk kunnen evolueren tijdens depositie/uitgloeiing. In dit artikel gebruiken we een continuümmodel om de typische metastabiele pitmorfologieën te onderzoeken die kunnen worden verwacht op Si(001), afhankelijk van de initiële diepte/vorm. Evolutie wordt voorspeld met behulp van een oppervlaktediffusiemodel, geformuleerd in een faseveldraamwerk, en het aanpakken van oppervlakte-energie-anisotropie. Er wordt aangetoond dat de resultaten typische metastabiele vormen die in de literatuur worden vermeld, mooi reproduceren. Bovendien blijkt dat evoluties op lange tijdschaal van putprofielen met verschillende diepten een vergelijkbaar kinetisch pad volgen. Het model wordt ook gebruikt om het geval van heteroepitaxiale groei te behandelen waarbij twee materialen betrokken zijn die worden gekenmerkt door verschillende facetten in hun evenwichtsvorm Wulff. Dit kan leiden tot significante veranderingen in morfologieën, zoals een rotatie van de put tijdens depositie, zoals blijkt uit Ge/Si-experimenten.

Achtergrond

Rooster-mismatched hetero-epitaxy van verschillende halfgeleiders (zoals Ge/Si of InGaAs/GaAs) kan leiden tot de vorming van 3D-eilanden, volgens de Stranski-Krastanow (SK) groeimodus. Hoewel de mogelijkheid om zulke stippen te verkrijgen door pure zelfassemblage [1, 2] bijzonder aantrekkelijk is en brede belangstelling wekte, werd al snel duidelijk dat willekeurige nucleatie toepassingen ernstig zou kunnen belemmeren, samen met verspreiding in grootte en vorm.

Decennia van onderzoek hebben geleid tot de ontwikkeling van een breed scala aan methoden om hetero-epitaxiale groei naar de vorming van geordende structuren te sturen [3-7]. Onder hen is aangetoond dat het gebruik van substraten met putjespatroon een van de meest veelzijdige methoden is om zowel een hoge ordening als groottecontrole van hetero-epitaxiale eilanden te bereiken [8-15].

Substraten met pitpatroon worden meestal vervaardigd met behulp van methoden zoals nano-imprintlithografie [16-18], e-beam-lithografie [13, 14] gecombineerd met reactieve ionenetsing (RIE) [19, 20] of nat chemisch etsen [21, 22], en nano-inspringing [23, 24], dwz door top-down benaderingen. Met deze methoden worden geordende patronen van putjes ontworpen met hoge precisie en, onder de juiste groeiomstandigheden [14, 25], leiden ze tot bijna perfecte laterale ordening.

Aangezien de werkelijke vorm van kuilen de energie van het systeem en, meer in het algemeen, eilandkiemvorming [26, 27] beïnvloedt, is het cruciaal om hun morfologie te beheersen. Dat is niet triviaal:putjes zijn immers gewoon gaten die in de ondergrond worden geboord. Dus bij voldoende hoge temperaturen wordt verwacht dat capillariteit [28] een morfologische evolutie teweegbrengt, die uiteindelijk tot volledige genezing leidt. Om reproduceerbare, langlevende metastabiele vormen te verkrijgen, worden in feite vaak gloeiprocessen of verdere afzetting van het substraatmateriaal na de initiële putvorming gebruikt [8, 26]. Merk op dat zelfs als een put eenmaal in vorm is gestabiliseerd, verdere evolutie kan worden aangedreven tijdens daadwerkelijke hetero-epitaxie [29, 30].

In dit werk willen we de evolutie beschrijven van substraten met een pitpatroon die worden aangedreven door reductie van oppervlakte-energie via oppervlaktediffusie. We passen een geschikte fase-veldbenadering [31] toe, waardoor de simulatie van lengte- en tijdschalen mogelijk is die compatibel zijn met de experimentele [32]. Het model is al gebruikt om rekening te houden met diffusie-beperkte kinetiek tijdens de morfologische evolutie in hetero-epitaxiale systemen [33–36]. Bovendien is aangetoond dat het de evolutie naar evenwicht goed beschrijft, inclusief realistische anisotrope oppervlakte-energieën [37-39].

Zonder verlies van algemeenheid, zullen we ons concentreren op de relevante gevallen van Si(001)-oppervlakken met pitpatroon, die uitgebreid zijn onderzocht in de literatuur [8, 10, 14, 30, 40, 41].

Het werk is als volgt georganiseerd. In de sectie "Phase-Field Model" illustreren we kort het faseveldmodel dat wordt gebruikt om de evolutie door oppervlaktediffusie te beschrijven, inclusief anisotrope oppervlakte-energie. Bovendien beschrijven we hoe de werkelijke Si Wulff-vorm wordt verwerkt in de overwogen benadering. In de sectie "Egaliseren van Si(001)-putten" wordt de verwachte afvlakking van Si(001)-putten, aangedreven door de reductie van oppervlakte-energie, besproken door verschillende initiële configuraties in overweging te nemen, waarbij de kinetische weg naar het evenwicht wordt geschetst. In de sectie "De vormverandering nabootsen als gevolg van overgroei van Ge", wordt een toepassing van de methode op een specifiek geval van hetero-epitaxiale groei die overeenkomt met de door oppervlakte-energie aangedreven vormverandering bij het afzetten van een dunne laag Ge op Si-pit overwogen. Conclusies en opmerkingen zijn samengevat in de sectie "Conclusies".

Methoden

Faseveldmodel

Het faseveldmodel houdt rekening met een continue-ordeparameter φ , variërend tussen φ =1 (vast) en φ =0 (vacuüm) [31, 32]. De aanpak is gebaseerd op een energiefunctionaal [37],

$$ \begin{aligned} F=&\int_{\Omega} \gamma(\hat{\mathbf{n}}) \left(\frac{\epsilon}{2} |\nabla \varphi|^{2 } + \frac{1}{\epsilon}B(\varphi) \right) d\mathbf{r} + \\ &+\int_{\Omega} \frac{\beta}{2\epsilon} \left( -\epsilon\nabla^{2}\varphi+\frac{1}{\epsilon}B'(\varphi)\right)^{2} d\mathbf{r}, \end{aligned} $$ (1)

met $\Omega \in \mathbb {R}^{3}$ het domein van de definitie van φ (r ) en r =(x ,j ,z ). De eerste term komt overeen met de interface-energie tussen fasen binnen het diffuse-interfacedomein gedefinieerd door φ , d.w.z. tot de oppervlakte-energie van de vaste fase. $\gamma (\hat {\mathbf {n}})$ is de oppervlakte-energiedichtheid, met $\hat {\mathbf {n}}$ de naar buiten wijzende oppervlaktenormaal, en ε de dikte van het grensvlak tussen fasen. B (φ )=18φ ² (1−φ )² is een dubbelputpotentieel met een minima in φ =0 en φ =1 zoals in Ref. [31]. De tweede term in Vgl. (1) is de Willmore-regularisatie die vereist is in het regime van sterke anisotropie om de vorming van scherpe hoeken te voorkomen [37, 38, 42]. β is een parameter die overeenkomt met de hoekafronding.

De evolutie voor φ reproduceert de diffusie-beperkte kinetiek van oppervlakken en wordt gegeven door het gedegenereerde Cahn-Hilliard-model, d.w.z.

$$ \frac{\partial \varphi}{\partial t}=D \nabla \left[ M(\varphi) \nabla \mu \right], $$ (2)

waar μ =δ F /δ φ is de chemische potentiaal, D is de diffusiecoëfficiënt, en M (φ )=(36/ε )φ ² (1−φ )² is de mobiliteitsfunctie beperkt tot het oppervlak. De vergelijking voor μ leest

$$ \begin{aligned} g(\varphi)\mu =\delta F/ \delta \varphi=&-\epsilon \nabla \cdot \left[\gamma(\hat{\mathbf{n}}) \nabla \varphi \right] + \frac{1}{\epsilon} \gamma(\hat{\mathbf{n}}) B'(\varphi) + \\&-\epsilon \nabla \cdot \left[|\ nabla \varphi|^{2} \nabla_{\nabla \varphi} \gamma(\hat{\mathbf{n}}) \right] + \\ &+\beta\left(-\nabla^{2} \ kappa + \frac{1}{\epsilon^{2}} B^{\prime\prime}(\varphi) \kappa \right), \end{aligned} $$ (3)

met κ =−ε ∇² φ +(1/ε )B ^′ (φ ) en g (φ )=30φ ² (1−φ )² [33, 37, 38]. Dit laatste is een stabiliserende functie die zorgt voor convergentie van de tweede orde in de grensvlakdikte, zonder de beschrijving van materiaaltransport via oppervlaktediffusie te beïnvloeden [43, 44]. Het profiel in de richting loodrecht op het grensvlak bij evenwicht wordt goed beschreven door

$$ \varphi(\mathbf{r})=\frac{1}{2}\left[1-\tanh \left(\frac{3 d(\mathbf{r})}{\epsilon} \right) \rechts], $$ (4)

waar d (r ) is de getekende afstand tot het midden van de interface tussen fasen. Deze vergelijking wordt gebruikt om de beginvoorwaarde in te stellen voor φ zoals hieronder aangegeven. We verwijzen naar het oppervlak van de vaste fase als de φ ∼0.5 iso-oppervlak. Alle geometrische eigenschappen van het beschouwde oppervlak kunnen worden afgeleid uit φ , zoals de naar buiten wijzende oppervlaktenormaal $\hat {\mathbf {n}}=- \nabla \varphi / | \nabla \varphi |$.

Anisotrope oppervlakte-energie

Om anisotrope oppervlakte-energieën te beschrijven, hebben we gekeken naar de definitie van de oppervlakte-energiedichtheid, $\gamma (\hat {\mathbf {n}})$, zoals geïntroduceerd in [38, 39]:

$$ \gamma(\hat{\mathbf{n}})=\gamma_{0} \left(1-\sum_{i}^{N} \alpha_{i} \left(\hat{\mathbf{n }} \cdot \hat{\mathbf{m}}_{i} \right)^{w_{i}} \Theta\left(\hat{\mathbf{n}} \cdot \hat{\mathbf{m }}_{i}\rechts) \rechts). $$ (5)

waarbij de voorkeursoriëntaties $\hat {\mathbf {m}}_{i}$, dwz de richtingen waarlangs de oppervlakte-energiedichtheid een minimum heeft, willekeurig kunnen worden ingesteld samen met hun relatieve diepten, _ik , met betrekking tot γ ₀ . De parameters w _ik controleer de uitbreiding van de regio's waar $\gamma (\hat {\mathbf {n}})<\gamma _{0}$ rond m _ik richtingen, d.w.z. ze zijn namelijk de breedtes van de minima (zie ook Ref. [38]).

Om rekening te houden met de specifieke anisotropie van Si-kristallen, stellen we de minimale energierichtingen in, m _ik , overeenkomend met 〈001〉, 〈113〉, 〈110〉 en 〈111〉 [45]. α _ik coëfficiënten, die de diepte van minima bepalen, worden verkregen door [39]

$$ \alpha_{i}=1-\left(\frac{\gamma_{i}}{\gamma_{\langle 001\rangle}}\right)\left(1-\alpha_{\langle 001 \rangle} \rechts), $$ (6)

waar α _〈001〉 =0.15 is ingesteld als referentie en de verschillende γ _ik komen overeen met de oppervlakte-energiewaarden van de bovengenoemde oriëntaties zoals gerapporteerd in Ref. [45]. Zonder het verlies van algemeenheid stellen we γ ₀ =1. Inderdaad, de verhoudingen van de minima en de sterkte van de anisotropie kunnen worden gecontroleerd door de α _ik waarden van Vgl. (6) en α _〈001〉 , terwijl γ ₀ speelt de rol van een prefactor in Vgl. (2), waardoor alleen de absolute tijdschaal van de evolutie wordt beïnvloed.

De breedte van de energieminima in Vgl. (5) zijn ingesteld op w _ik =50 voor alle minima-richtingen, behalve voor w _〈113〉 =100 [39]. Volgens deze definitie van de parameters worden scherpe hoeken voorspeld in de Wulff-vorm, d.w.z. de anisotropie van de oppervlakte-energie is "sterk" [38, 42, 46]. Daarom is de Willmore-regularisatie strikt noodzakelijk om de simulaties uit te voeren. De β waarde bepaalt de uitbreiding van het afgeronde gebied op de hoeken, waarvan bekend is dat ze een straal hebben die evenredig is met $\sqrt {\beta }$ [37]. Om simulaties uit te voeren, is de lengteschaal ingesteld door de afronding op de hoek door β moet groter zijn dan de resolutie van de ruimtelijke discretisatie van de numerieke methode. Het is echter vermeldenswaard dat kleine facetten die mogelijk aanwezig zijn in de Wulff-vorm met een extensie in de volgorde $\sqrt {\beta }$ verborgen kunnen zijn bij gebruik van te grote β waarden en kleinschalige facetten met voorkeursoriëntaties die daadwerkelijk aanwezig zijn in de Wulff-vorm. In dit werk stellen we β =0,005. Afhankelijk van de grootte van het simulatiedomein, gespecificeerd in het volgende, stelt deze waarde ons in staat om haalbare ruimtelijke discretisatie toe te passen. Bovendien zijn alle preferentiële oriëntaties die Vgl. (5) en (6) worden weergegeven. Aan de andere kant kunnen mogelijke facetten met kleinere schalen dan ∼0,07 niet worden gereproduceerd vanwege de verlenging van de hoekafronding.

Initiële morfologie en simulatie-instelling

Om elke morfologische evolutie te onderzoeken met behulp van het faseveldmodel dat in deze sectie is gedefinieerd, is een goede beginvoorwaarde voor φ moet worden ingesteld. We beschouwen hier een gladde putgeometrie uitgehouwen in een (001) vlak oppervlak, met een referentiekader ingesteld op $\hat {\mathbf {x}}=\,[\!100]$, $\hat {\ mathbf {y}}=\,[\!010]$, en $\hat {\mathbf {z}}=\,[\!001]$. In het bijzonder beschouwen we een cirkelvormig (001) oppervlak met straal L op een hoogte h ₀ −H , vloeiend verbonden met het omringende (001) vlakke oppervlak op hoogte h ₀ . Zo'n geometrie is ingesteld als beginvoorwaarde voor φ door gebruik te maken van Eq. (4) met d (r ) de getekende afstand vanaf het oppervlak Γ (x ,j ) gedefinieerd door

$$ \Gamma(x,y)=\left\{ \begin{aligned}h_{0} - &H &\qquad r \leq L \\ h_{0} - &H \exp \left[ -\frac {1}{2}\frac{|\mathbf{s}-\bar{\mathbf{s}}|^{2}}{\sigma^{2}} \right] &\qquad r> L \end {uitgelijnd} \rechts. $$ (7)

met $r=\sqrt {x^{2}+y^{2}}$ en

$$ \mathbf{s}=(x,y), \qquad \bar{\mathbf{s}} =\frac{R}{r} (x,y). $$ (8)

R =H /4L wordt gedefinieerd als een aspectratioparameter, terwijl σ is een parameter die de uitbreiding van de continue verbinding tussen de bodem van de put en het vlakke gebied eromheen regelt. Deze parameter wordt hier ingesteld op σ =L /2.

In Fig. 1 is de beginvoorwaarde aangenomen voor φ wordt geïllustreerd. Afbeelding 1a toont Γ (x ,0) profielen met verschillende waarden van R . Figuur 1b toont de definitie van φ door middel van vgl. (4) in een 3D-parallelpipedumdomein. Dit paneel toont in het bijzonder een dwarsdoorsnede die door het midden van het hele domein loopt. Het linkerdeel toont het gebied dat overeenkomt met de vaste fase, d.w.z. het gebied waar φ> 0,5, waardoor het oppervlak wordt onthuld dat overeenkomt met de oorspronkelijke pitmorfologie. Het rechterdeel illustreert de waarden van φ in het gehele 3D-domein, dus in de bulkfasen en binnen de continue overgang daartussen.

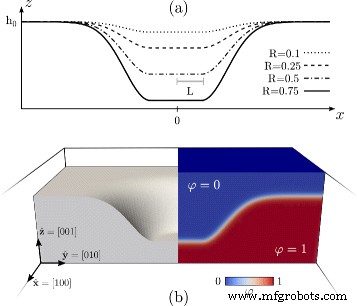
Beginconditie voor het faseveldmodel, dat lijkt op een gladde put aan het (001) oppervlak van een vaste film. een Γ (x ,0) profielen van Eq. (7) verkregen voor verschillende R waarden. b Definitie van φ in het 3D-domein dat is aangenomen voor numerieke simulaties. Het wordt verkregen uit Vgl. (4) met d (r ) de ondertekende afstand van Γ (x ,j ) met R =0,5. Links de vaste fase waar φ> 0,5 wordt weergegeven. Aan de rechterkant een kleurenkaart met φ in het 3D-domein wordt gerapporteerd

Numerieke simulaties worden uitgevoerd om vergelijkingen te integreren. (2) en (3). Ze worden uitgevoerd met behulp van de eindige-elementenmethode (FEM) toolbox AMDiS [47, 48], met een semi-impliciet integratieschema en mesh-verfijning op de interface [33, 38, 49]. Periodieke randvoorwaarden worden gesteld langs $\hat {\mathbf {x}}$ en $\hat {\mathbf {y}}$ richtingen. No-flux (Neumann) randvoorwaarden worden aan de boven- en onderkant van het simulatiedomein in de $\hat {\mathbf {z}}$ richting gezet. De tijdschaal van de evolutie wordt geschaald met een factor 1/D , wat overeenkomt met set D =1. In het volgende verwijzen we naar de tijd van simulaties in willekeurige eenheden. De grootte van de put is willekeurig ingesteld op L =1, terwijl de interfacedikte is ingesteld op ε =0.2.

Resultaten en discussie

Egaliseren van Si(001)-putten

In deze sectie illustreren we de resultaten met betrekking tot de morfologische veranderingen tijdens de evolutie van Si(001)-substraten met pitpatroon. Het hierboven beschreven model maakt de beschrijving van het specifieke geval van silicium mogelijk door middel van de definitie van de anisotrope oppervlakte-energie zoals in de sectie "Anisotrope oppervlakte-energie". We verwachten dat de volgende resultaten vanuit een kwalitatief oogpunt geldig zijn voor elke grootte, op voorwaarde dat het systeem groot genoeg is om een continuümbenadering ($\gtrsim 10$ nm) [32] aan te nemen en de vorm kan worden geparametreerd door de beeldverhouding R vergelijkbaar met Fig. 1 a. De werkelijke lengteschaal kan worden bekeken door de L . in te stellen parameter naar de corresponderende in reële eenheden, L ^r . De real-time schaal kan dan worden beschreven door rekening te houden met reële waarden van D en γ ₀ en vermenigvuldigen met de L ^r lengte, d.w.z. door te schalen met L ^r /L met L unitair zoals hierboven gespecificeerd.

Laten we ons eerst concentreren op de eerste stadia van de evolutie. De beginvoorwaarde ingesteld door Vgl. (7) bestaat uit een profiel dat geen voorkeursoriëntatie van het oppervlak vertoont. Bij het beschouwen van de evolutie door oppervlaktediffusie aangedreven door de reductie van een anisotrope oppervlakte-energie, wordt een facettering van het initiële profiel verwacht. Dit wordt geïllustreerd in Fig. 2 waar de facetten van twee profielen met R =0,25 in Fig. 2 a en R =0,5 in Fig. 2b worden gerapporteerd. Een kleurenschaal illustreert de waarden $\gamma (\hat {\mathbf {n}})$ aan het oppervlak. Dit maakt het mogelijk om de facetten te identificeren als de regio's met een bijna uniforme oppervlakte-energiedichtheid die overeenkomt met de minima van Vgl. (5), begrensd door gelokaliseerde regio's met hoge waarden van $\gamma (\hat {\mathbf {n}})$. Volgens de initiële aspectverhouding van de put vormen zich verschillende facetten. Voor de kleinere R blijft het facet (001) aan de onderkant een vierkante vorm aannemen. De randen van de put worden begrensd door vier {113} facetten die verbonden zijn door kleine, driehoekige {110} facetten. Volgens de grotere beeldverhouding is er een groter gefacetteerd oppervlak aanwezig bij het overwegen van R =0,5, waardoor preferentiële oriëntaties met een hogere helling ten opzichte van het (001) oppervlak kunnen worden weergegeven. In het bijzonder zorgt de initiële vorm voor de aanwezigheid van {111} facetten die zich vormen tussen twee {113} facetten dicht bij de bodem en bij het platte gebied. Daartussen vormen zich brede {110} facetten.

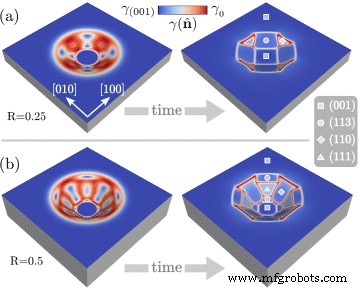
Facetisering van het initiële profiel zoals gedefinieerd in de sectie "Initial Morfology and Simulation Setup" volgens oppervlaktediffusie en $\gamma (\hat {\mathbf {n}})$ die de oppervlakte-energie van Si reproduceert. Er worden twee verschillende initiële morfologieën beschouwd:a R =0,25 en b R =0,5. Op de gefacetteerde morfologieën worden symbolen gebruikt om de families van facetten te identificeren. De kleurenschaal toont de waarden van $\gamma (\hat {\mathbf {n}})$ aan het oppervlak

De resultaten vermeld in Fig. 2 tonen de mogelijkheid om gefacetteerde putmorfologie te voorspellen volgens de aspectverhouding of, in het algemeen, volgens de initiële morfologie. We onderzoeken nu ook de dynamiek op de lange tijdschaal en inspecteren de morfologische evolutie tot aan het evenwicht [38]. Dit wordt geïllustreerd in Fig. 3, waar we ons concentreren op de diepste put die tot nu toe is overwogen, d.w.z. met R =0,5, en de belangrijkste morfologische veranderingen worden getoond. In het bijzonder worden respectievelijk perspectief- en bovenaanzichten van de verschillende morfologieën die tijdens de evolutie zijn verkregen, gerapporteerd in Fig. 3 a, b. In de eerste fase van deze simulatie observeren we het verdwijnen van de steilste {111} facetten en de vergroting van aangrenzende {113} facetten. Vervolgens worden de laatste samengevoegd en begint de krimp van {110} facetten. Deze blijken in latere stadia te verdwijnen nadat ze een driehoekige vorm hebben aangenomen, waardoor de put van bovenaf een vierkante omtreklijn krijgt. Ook verdwijnen {113} facetten uiteindelijk en wordt een globale afvlakking bereikt. De real-time schaal verkregen in deze simulatie kan worden geschat met gegevens uit de literatuur. In het bijzonder kunnen we overwegen D bepaald door de wet van Arrhenius met prefactor en activeringsenergie van Ref. [50], waarbij ook rekening wordt gehouden met thermische fluctuaties. γ ₀ is ingesteld op $\gamma (\hat {\mathbf {n}})\sim 8.7$ eV/nm² wanneer $\hat {\mathbf {n}}=(001)$ [51] uit Vgl. (5), dat wil zeggen, γ ₀ =10,2 eV/nm² . De andere materiaalafhankelijke coëfficiënten van oppervlaktediffusie [28], d.w.z. atomair volume en dichtheid aan het oppervlak, zijn ingesteld om het geval van Si te reproduceren. Volgens deze waarden is de verwachte duur van het gehele proces bij hoge temperatuur T ∼1100−1200 °C voor L ^r van tientallen nanometers is in de orde van uren.

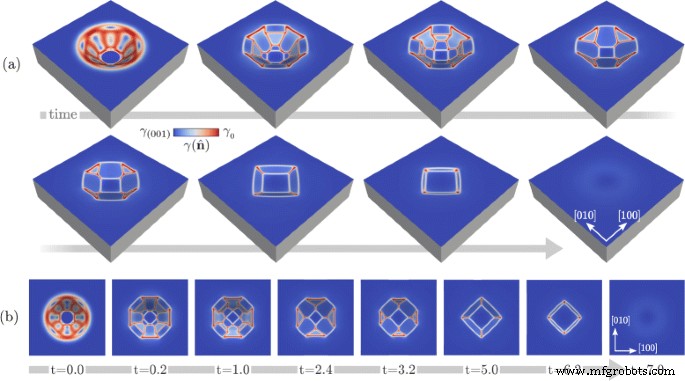
Evolutie naar het evenwicht voor een Si-pit met een initiële morfologie zoals in Fig. 2b. een Perspectiefaanzicht met de belangrijkste morfologische veranderingen. b Bovenaanzicht van de morfologieën in paneel a . De tijd gerapporteerd in paneel b wordt uitgedrukt in willekeurige eenheden. De kleurenschaal toont de waarden van $\gamma (\hat {\mathbf {n}})$ aan het oppervlak

Naast de specifieke morfologische veranderingen die tijdens de evolutie optreden, moeten twee hoofdkenmerken worden opgemerkt. Ten eerste leidt de evolutie tot de verwachte globale afvlakking van het oppervlak, en dit gebeurt met het geleidelijk verdwijnen van steile facetten die worden vervangen door ondiepere. Hoewel dit gedrag alleen kan worden afgeleid door argumenten over energieminimalisatie en verlaging van de beeldverhouding, is het de moeite waard om erop te wijzen dat de volledige evolutie hier wordt gegeven, waarbij de aanwezigheid van vergelijkbare facetten maar met verschillende relatieve afmetingen wordt behandeld. Dit is in overeenstemming met het feit dat de morfologieën die tijdens de evolutie zijn verkregen, overeenkomen met configuraties die niet in evenwicht zijn en een pad definiëren naar het globale energieminimum. Dan, ondanks dat de verwachte facetten en hun energieën bekend zijn, kan de specifieke morfologie op een bepaald punt van de evolutie alleen worden beschreven door rekening te houden met de dynamiek en niet alleen door globale energieminimalisatie te overwegen [38].

Het tweede belangrijke punt dat wordt getoond door de resultaten die in figuur 3 worden vermeld, betreft de tussenstadia. Wanneer de vorm tijdens de evolutie een geometrie nadert met een diepte vergelijkbaar met het initiële profiel verkregen met R =0,25, d.w.z. op t ∼3.2 lijkt de morfologie die wordt veroorzaakt door de energieminimalisatie zeer sterk op wat wordt gerapporteerd in Fig. 2b, zelfs wanneer wordt uitgegaan van een initiële configuratie met een significant verschil in diepte (dubbel in dit geval). Dit suggereert het bestaan van een gemeenschappelijk kinetisch pad naar de uiteindelijke afvlakking, die wordt bereikt na de eerste snelle facettering van de initiële morfologie. Dit argument wordt feitelijk bevestigd en verder geïllustreerd in de grafieken van Fig. 4. Hier wordt het monotone energieverval tijdens de evolutie na de eerste facettering gerapporteerd bij het beschouwen van pits met R gelijk aan 0,1, 0,25, 0,5 en 0,75 zoals in Fig. 1a. In figuur 4a wordt de tijdschaal, uitgedrukt in willekeurige eenheden, beschouwd. In Fig. 4b worden dezelfde energieveranderingen gerapporteerd met een juiste verschuiving van de tijdschaal, waarbij het vergelijkbare energieverval wordt benadrukt bij het naderen van vergelijkbare aspectverhoudingen van de structuur. $t^{*}_{R}$ wordt gedefinieerd als het tijdstip waarop het vlakke oppervlak wordt verkregen, dwz het tijdstip waarop het globale energieminimum wordt bereikt, dat voor elke simulatie anders is, zoals weergegeven in Fig. 4 een. Zoals te zien is in deze grafiek, overlapt het energieverval bijna voor R ≤0.5. Een zeer klein verschil wordt alleen waargenomen bij het overwegen van R =0,75, waarvan de resultaten van het energieverval nog steeds erg dicht bij de andere krommen liggen en de verschillen in principe verdwijnen voor $t \gtrsim 5.0$. Het is vermeldenswaard dat voor grote afwijkingen van de initiële configuratie, namelijk met R ≫1, dergelijke geometrieën kunnen anders evolueren met verschillende effecten op tijdschalen en morfologieën [52, 53]. Bovendien is het bekend dat topologische veranderingen in extreme gevallen optreden, bijvoorbeeld bij zeer diepe greppels, waardoor het onmogelijk is om het globale evenwicht te bereiken met een vlak (001) oppervlak [34, 39, 54].

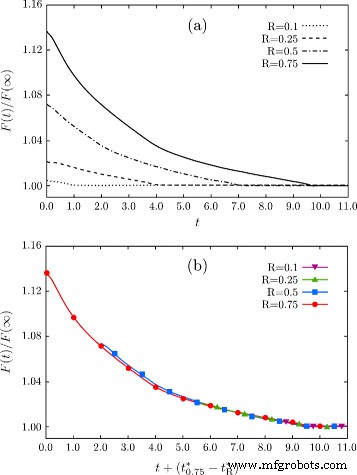
Energie neemt af tijdens de evolutie van putgeometrieën. een F (t ) genormaliseerd door de energie van het platte (001) oppervlak verkregen als laatste fase van de evolutie. Energieverval verkregen uit de simulaties met verschillende R voor het initiële profiel, namelijk van R =0,1 tot R =0,75, worden weergegeven. Tijd wordt uitgedrukt in willekeurige eenheden. b Curven zoals in paneel a verschoven om overeen te komen met $t_{R}^{*}$, d.w.z. het tijdstip waarop de globale afvlakking van de put wordt bereikt, is afhankelijk van R

De vormen die zijn verkregen in de simulaties die in deze secties worden gerapporteerd, zullen naar verwachting worden waargenomen in experimenten, met name wanneer de verwerking omstandigheden omvat die dicht bij de thermodynamische limiet liggen. Sommige van de in Fig. 3 gerapporteerde morfologieën komen in feite overeen met de omtrek van Si(001)-substraten met pitpatroon. Bijvoorbeeld een morfologie gemaakt van een breed (001) oppervlak begrensd door smalle {113} facetten zoals in Fig. 3 op t ∼5.0 worden waargenomen bij het overwegen van Si(001)-substraten met pitpatroon met een aspectverhouding van 0,05<R <0.1 zoals in Ref. [10, 30]. Ook lijkt de relatieve extensie van de facetten in de bovengenoemde fase van de simulatie van Fig. 3 sterk op wat werd gerapporteerd in deze experimentele werken. Deze overeenkomst tussen simulaties en experimenten beoordeelt verder de theoretische beschrijving van oppervlaktediffusie die hier is aangenomen. We hebben ons echter gericht op de algemene kenmerken van het proces en een meer gedetailleerde vergelijking met specifieke experimenten is buiten het doel van dit werk.

De vormverandering nabootsen als gevolg van Ge-overgroei

Zoals vermeld in de inleiding, is een van de belangrijkste toepassingen van Si-sjablonen met pitpatroon de beheersing van de groei van zelf-geassembleerde eilanden [55]. Dit geldt in het bijzonder bij het overwegen van de positionering van Ge of Si_{1 − c} Ge_c eilanden op Si(001)-substraten [6]. Met de methodologie die in de vorige sectie is aangenomen, kunnen we de morfologische veranderingen inspecteren die verband houden met de eigenaardige kenmerken van de oppervlakte-energie. Daarom kunnen we, door uit te gaan van een juiste initiële configuratie die lijkt op de echte morfologie van een Si-pit en rekening te houden met de verschillen in de verwachte oppervlakte-energiedichtheid bij het deponeren van een ander materiaal, voorspellen wat de overeenkomstige bijdrage is aan morfologische veranderingen.

De casestudy bestaat hier uit de begroeiing van Ge over een Si(001)-putpatroon met een aspectverhouding dichtbij 0,1. Het profiel van Fig. 3 bij t =5.0 wordt beschouwd als een initiële morfologie. Vervolgens wordt een oppervlakte-energie ingesteld die ook een minima in de 〈105〉-richtingen omvat. Deze definitie van $\gamma (\hat {\mathbf {n}})$ bootst de aanwezigheid na van de meest favoriete oriëntatie met kleine hellingen in Ge/Si(001)-systemen [56-58]. De hoge stabiliteit van {105} facetten is te wijten aan het samenspel tussen oppervlaktereconstructie en spanningseffecten gerelateerd aan de roostermismatch tussen de epilaag en het substraat [59-61]. De oppervlakte-energiedichtheidswaarde die moet worden gebruikt in Vgl. (6) is overgenomen uit Ref. [58] in de limiet van een dikke Ge-laag. Merk op dat andere facetten die een oppervlakte-energie hebben die dichter bij de (001) ligt, zoals {1 1 10}, hier worden verwaarloosd. Omdat de hoeken tussen de 〈105〉 en de [001] richtingen erg klein zijn, w _ik parameters die groter zijn dan de eerder aangenomen parameters zijn vereist om de energieminima van Vgl. goed te beschrijven. (5) [38]. In het bijzonder stellen we w _{105} =w _{001} =500.

In Fig. 5 wordt de evolutie door oppervlaktediffusie met de nieuwe definitie van $\gamma (\hat {\mathbf {n}})$ gerapporteerd. Figuur 5a toont de morfologische evolutie van het oppervlak met een vergroting van de z -as met een factor 5. In de eerste fasen vormen zich {105} facetten tussen de {113} facetten die aanwezig zijn in het initiële profiel. Omdat 〈105〉-oriëntaties de minimale energie hebben zoals ook geïllustreerd in figuur 5b, strekken de corresponderende facetten zich uit terwijl {113} facetten krimpen. In latere stadia vormt zich alleen een put begrensd door {105} facetten met nog steeds een (001) oppervlak aan de onderkant. Vanuit het bovenaanzicht zoals in Fig. 5b resulteert de verandering in de morfologie in een rotatie van de omtrek van de put met 45°. Dit wordt feitelijk waargenomen tijdens de afzetting van Ge op substraten met Si-patroon in experimenten [41] of tijdens de spontane groei van kuilen als gevolg van defecten of onzuiverheden [40]. De vorming van {105} facetten blijkt ook een favoriete nucleatieplaats te zijn voor verdere groei van Ge-dots [30]. De evolutie geïllustreerd in Fig. 5 toont aan dat een verandering in vorm die leidt tot de rotatie van de putomtrek alleen kan worden bereikt door reductie van oppervlakte-energie. Verwacht wordt dat dit de werkelijke situatie is in omstandigheden die bijna in evenwicht zijn, wanneer thermodynamische drijvende krachten worden gedomineerd door oppervlaktebijdragen, d.w.z. voor kleine Ge-volumes. Om het proces volledig te beschrijven, moeten elasticiteitseffecten, vermenging en de groei van de vaste fase worden opgenomen [32]. Het is ook vermeldenswaard dat zelfs ondiepere Si-pits worden gebruikt in experimenten, waarbij facetten met normalen worden getoond langs {11n } routebeschrijving, met 5<n <10 [41] (d.w.z. {1 1 10} facetten). Putgeometrie begrensd door deze facetten zou tot een vergelijkbare evolutie leiden, omdat ze overeenkomen met wat werd aangenomen als initiële configuratie van Fig. 4 met slechts een kleinere helling ten opzichte van het (001) vlak.

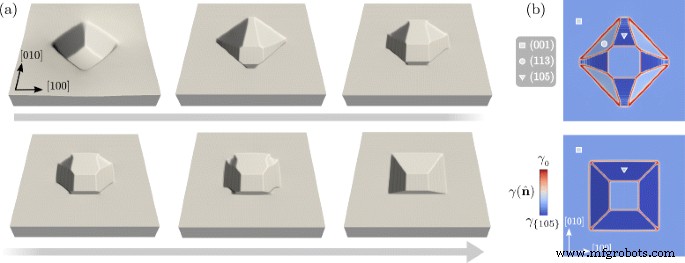
Evolutie van het profiel in Fig. 3 bij t =5.0, met een definitie van de oppervlakte-energie inclusief 〈105〉-oriëntaties. een Oppervlakteprofielen in representatieve stadia van de evolutie naar de vorming van een put die alleen wordt begrensd door {105} facetten. z -as wordt vergroot met een factor 5. b Bovenaanzicht met de $\gamma (\hat {\mathbf {n}})$ waarden aan de oppervlakte. De tweede en laatste fase van paneel a worden respectievelijk in het bovenste en onderste deel gerapporteerd. Symbolen zoals in Fig. 2 worden gebruikt om verschillende families van facetten te identificeren

Conclusies

In dit werk hebben we een continuümmodel op basis van oppervlaktediffusie gebruikt om de temporele evolutie van putten te onderzoeken die zijn uitgegraven in een Si(001)-substraat. Door (sterke) anisotropie van oppervlakte-energie aan te pakken, met een parametrisering op basis van de bekende Si Wulff-vorm, hebben we typische metastabiele configuraties voorspeld in overeenstemming met experimenten, inclusief het geval waarin depositie van een ander materiaal nieuwe stabiele facetten introduceert. The entire evolution towards the global flattening of the pit has been illustrated, and it is found to follow the same kinetic pathway also when considering pits with different initial depths. We believe that the model can be predictive also for initial configurations strongly deviating from the ones which we have analyzed as examples. As a consequence, the present approach can be useful in designing experiments based on still-unexplored pit shapes. Furthermore, the model is general and can be easily adapted to different substrates upon re-parametrizing the surface energy.

Weinig gelaagde MoS2/acetyleenzwarte composiet als een efficiënt anodemateriaal voor lithium-ionbatterijen Temperatuurafhankelijkheid van Spin-Split Peaks in Transverse Electron Focusing

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal