MATLAB - Grafisch

In dit hoofdstuk worden de plot- en grafische mogelijkheden van MATLAB verder onderzocht. We zullen bespreken −

• Staafdiagrammen tekenen
• Contouren tekenen
• Driedimensionale plots

Staafdiagrammen tekenen

De balk commando tekent een tweedimensionaal staafdiagram. Laten we een voorbeeld nemen om het idee te demonstreren.

Voorbeeld

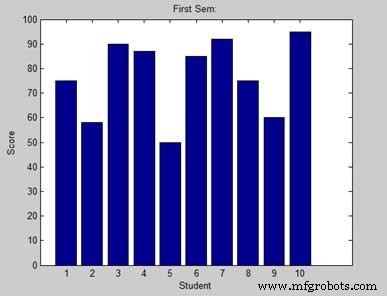
Laten we een denkbeeldig klaslokaal hebben met 10 leerlingen. We weten dat het percentage cijfers dat deze studenten behalen 75, 58, 90, 87, 50, 85, 92, 75, 60 en 95 zijn. We zullen het staafdiagram voor deze gegevens tekenen.

Maak een scriptbestand en typ de volgende code −

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

Wanneer u het bestand uitvoert, geeft MATLAB het volgende staafdiagram weer −

Contouren tekenen

Een contourlijn van een functie van twee variabelen is een kromme waarlangs de functie een constante waarde heeft. Contourlijnen worden gebruikt voor het maken van contourkaarten door punten met gelijke hoogte boven een bepaald niveau, zoals gemiddeld zeeniveau, met elkaar te verbinden.

MATLAB biedt een contour functie voor het tekenen van contourkaarten.

Voorbeeld

Laten we een contourkaart genereren die de contourlijnen toont voor een bepaalde functie g =f(x, y). Deze functie heeft twee variabelen. We zullen dus twee onafhankelijke variabelen moeten genereren, d.w.z. twee datasets x en y. Dit doe je door het meshgrid . aan te roepen commando.

Het meshraster commando wordt gebruikt voor het genereren van een matrix van elementen die het bereik over x en y geven, samen met de specificatie van increment in elk geval.

Laten we onze functie g =f(x, y) plotten, waarbij −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Laten we voor beide waarden een toename van 0,1 nemen. De variabelen zijn ingesteld als −

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

Ten slotte moeten we de functie toewijzen. Laat onze functie zijn:x ² + y ²

Maak een scriptbestand en typ de volgende code −

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
contour(x,y,g)                         % call the contour function
print -deps graph.eps

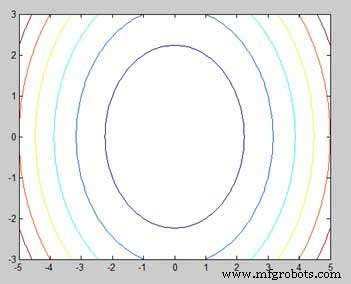
Wanneer u het bestand uitvoert, geeft MATLAB de volgende contourkaart weer −

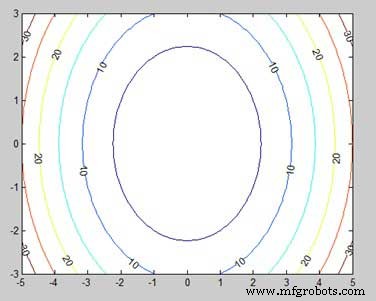
Laten we de code een beetje aanpassen om de kaart op te fleuren

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

Wanneer u het bestand uitvoert, geeft MATLAB de volgende contourkaart weer −

Driedimensionale percelen

Driedimensionale plots geven in feite een oppervlak weer dat wordt gedefinieerd door een functie in twee variabelen, g =f (x,y).

Zoals eerder, om g te definiëren, creëren we eerst een reeks (x,y) punten over het domein van de functie met behulp van het meshgrid opdracht. Vervolgens wijzen we de functie zelf toe. Ten slotte gebruiken we de surf commando om een ​​oppervlakteplot te maken.

Het volgende voorbeeld demonstreert het concept −

Voorbeeld

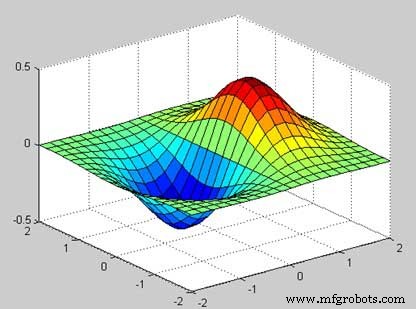
Laten we een 3D-oppervlaktekaart maken voor de functie g =xe ^{-(x 2 + y 2 )}

Maak een scriptbestand en typ de volgende code −

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Wanneer u het bestand uitvoert, geeft MATLAB de volgende 3D-kaart weer −

U kunt ook de mesh . gebruiken commando om een ​​driedimensionaal oppervlak te genereren. Echter, de surf commando geeft zowel de verbindingslijnen als de vlakken van het oppervlak in kleur weer, terwijl de mesh commando creëert een wireframe-oppervlak met gekleurde lijnen die de bepalende punten verbinden.