Current Divider Rule (CDR) - Opgeloste voorbeelden voor AC- en DC-circuits

Huidige divisie "CDR" voor resistieve, inductieve en capacitieve circuits

Wat is Current Divider Rule (CDR)?

Als een aantal elementen parallel worden geschakeld, wordt de stroom verdeeld in een aantal parallelle paden. En de spanning is hetzelfde voor alle elementen die gelijk zijn aan de bronspanning.

Met andere woorden, wanneer de stroom door meer dan één parallel pad gaat (de spanningsdelerregel "VDR" of spanningsdeling wordt gebruikt om de spanning in de serieschakelingen te berekenen), de stroomverdeling in elk pad. De waarde van de stroom die door een bepaalde tak gaat, hangt af van de impedantie van die tak.

De huidige delerregel of huidige delingsregel is de belangrijkste formule die veel wordt gebruikt om circuits op te lossen. We kunnen de stroom vinden die door elke tak gaat als we de impedantie van elke tak en de totale stroom kennen.

De stroom vloeit altijd door de laagste impedantie. De stroom heeft dus een omgekeerde relatie met de impedantie. Volgens de wet van ohm wordt de stroom die het knooppunt binnenkomt, omgekeerd evenredig aan de impedantie verdeeld.

Het betekent dat de impedantie met een kleinere waarde een grotere stroom heeft omdat de stroom het pad met de minste weerstand heeft gekozen. En de weerstand met een grotere waarde heeft de minste stroom.

Volgens de circuitelementen kan de huidige delerregel weerstanden, inductoren en condensatoren beschrijven.

Huidige scheidingsregel voor resistieve circuits

Laten we, om de resistieve stroomdelerregel te begrijpen, een circuit nemen waarin de weerstanden parallel zijn geschakeld. Het schakelschema wordt weergegeven in de onderstaande afbeelding.

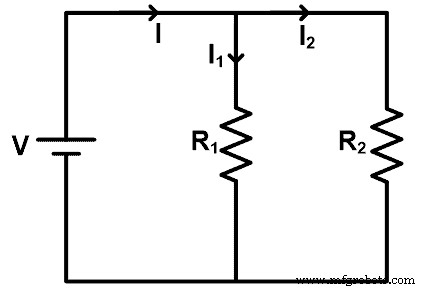
In dit voorbeeld een DC-bronvoeding voor alle weerstanden. De spanning van weerstanden is hetzelfde als de bronspanning. Maar door een parallelle verbinding verdeelt de stroom zich in verschillende paden. De stroom verdeelt zich bij elk knooppunt en de waarde van de stroom hangt af van de weerstand.

We kunnen de waarde van de stroom die door elke weerstand gaat direct vinden met behulp van de stroomverdelingsregel.

In dit voorbeeld is de hoofdstroom geleverd door de bron I. En deze wordt verdeeld in twee weerstanden R₁ en R₂ . De stroom gaat door de weerstand R₁ is ik₁ en de stroom gaat door de weerstand R₂ is ik₂ .

Omdat de weerstanden parallel zijn geschakeld. Dus de equivalente weerstand is R_eq .

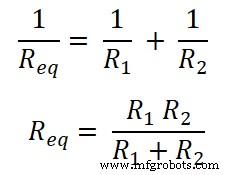
Nu, volgens de wet van Ohm;

V =I R_eq

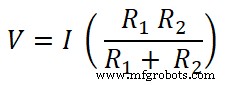
Beide weerstanden zijn parallel geschakeld met een gelijkstroombron. Daarom is de spanning over de weerstand hetzelfde als de bronspanning. En de stroom die door de weerstand R₁ . gaat is ik₁ .

Dus, voor weerstand R₁;

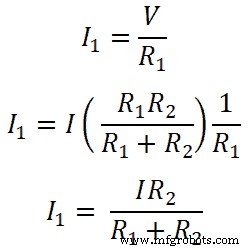
Evenzo, voor resister R₂;

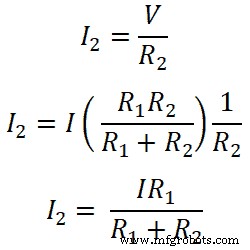
Deze vergelijking toont dus een huidige delerregel voor parallel geschakelde weerstand. Uit deze vergelijkingen kunnen we zeggen dat de stroom die door de weerstand gaat, gelijk is aan de verhouding van vermenigvuldiging van de totale stroom en tegengestelde weerstand met de totale weerstand.

Gerelateerde berichten:

• De stelling van Thevenin. Stap voor stap handleiding met opgelost voorbeeld
• De stelling van Norton. Stap voor stap handleiding met opgelost voorbeeld

Huidige scheidingsregel voor inductieve circuits

Als inductoren parallel zijn aangesloten, kunnen we de stroomdelerregel toepassen om de stroom te vinden die door elke inductor gaat. Om de huidige delerregel te begrijpen, nemen we een circuit waarin de inductoren parallel zijn geschakeld, zoals weergegeven in de onderstaande afbeelding.

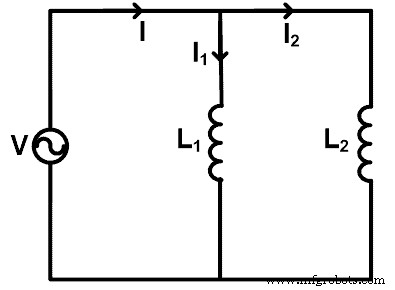
Hier, twee inductoren (L₁ en L₂ ) zijn parallel geschakeld met een bronspanning V. De totale stroom die door de bron gaat is I ampère. De stroom gaat door de spoel L₁ is ik₁ en de stroom gaat door de spoel L₂ is ik₂ .

Nu moeten we de vergelijkingen vinden voor de huidige I₁ en ik₂ . Daarvoor vinden we de equivalente inductantie L_eq;

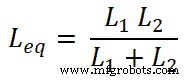
We weten dat de totale stroom die door het circuit gaat gelijk is aan I en het is gelijk aan;

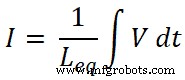
Dus,

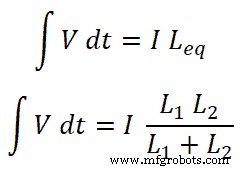
Nu, voor spoel L₁ , stroom die door deze spoel gaat is I₁;

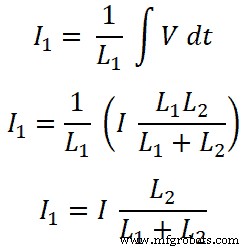
Voor spoel L₂;

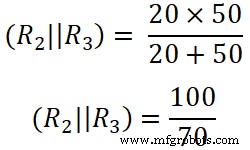
De huidige delerregel voor de inductor is hetzelfde als de huidige delerregel voor de weerstanden.

Huidige scheidingsregel voor capacitieve circuits

Als de condensatoren parallel zijn aangesloten, kunnen we de stroom door elke condensator vinden met behulp van de stroomdelerregel. Om de huidige delerregel voor de condensator te begrijpen, nemen we een voorbeeld waarin de condensatoren parallel zijn geschakeld, zoals weergegeven in de onderstaande afbeelding.

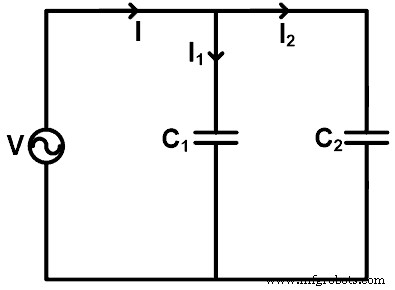
Hier, twee condensatoren (C₁ en C₂ ) zijn parallel geschakeld met een spanningsbron V. De stroom gaat door de condensator C₁ is I_1, en de stroom gaat door de condensator C₂ is ik₂ . De totale stroom geleverd door de bron is I.

Nu moeten we de vergelijkingen vinden voor de huidige I₁ en ik₂ . Daarvoor zullen we de equivalente capaciteit C_eq . vinden;

C_eq =C ₁ + C ₂

We kennen de vergelijking voor de stroom die door de condensator gaat. En de vergelijking voor de totale stroom geleverd door de bron is;

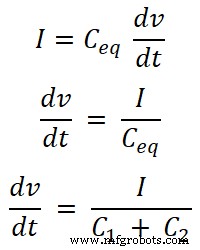
Voor condensator C₁ , de stroom die door deze condensator gaat is I₁;

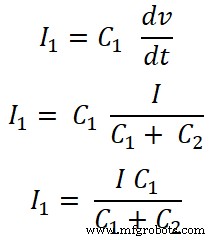
Voor condensator C₂;

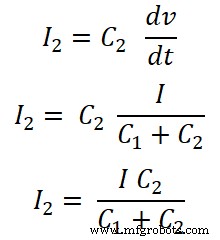
De huidige delerregel voor de condensator verschilt enigszins van de huidige delerregel voor de inductor en weerstand.

In de regel van de stroomverdeler van de condensator is de stroom die door een condensator gaat een verhouding van de totale stroom vermenigvuldigd met die condensator tot de totale capaciteit.

Opgeloste voorbeelden voor AC- en DC-circuits met CDR

Huidige duikerregel voor gelijkstroomcircuit

Voorbeeld:1

Zoek de stroom die door elke weerstand gaat volgens de stroomdelerregel voor het gegeven netwerk.

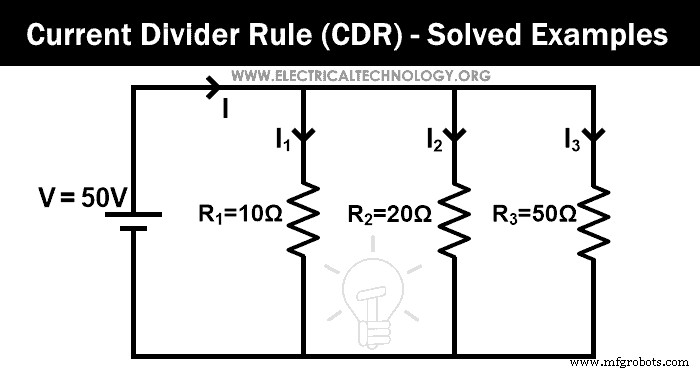
In dit voorbeeld zijn drie weerstanden parallel geschakeld. Eerst vinden we de equivalente weerstand.

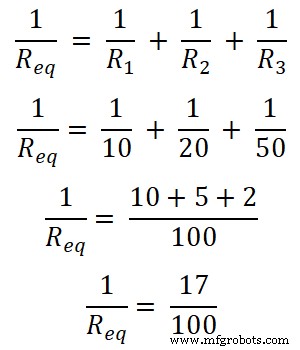
R_eq = 100/17

R_eq = 5.882 Ω

De totale stroom geleverd door de bron is I. Dus volgens de wet van ohm;

V =I R_eq

50V =I (5.882Ω)

I = 50V / 5.882Ω

I = 8.5A

Nu passen we de huidige delerregel toe op de eerste weerstand (10 Ω), en de stroom die door deze weerstand gaat is I₁;

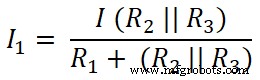
Hier R₂ en R₃ zijn parallel geschakeld. We moeten dus de equivalente weerstand vinden tussen R₂ en R₃ .

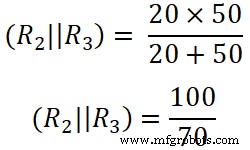
(R ₂ || R ₃ ) =14,285 Ω

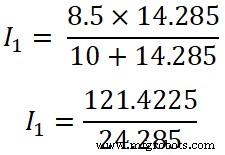
Ik ₁ =4,9999 ≈ 5 A

Op dezelfde manier passen we de stroomdelerregel toe op de tweede weerstand (20 Ω), en de stroom die door deze weerstand gaat is I₂;

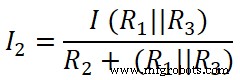
Hier,

(R ₁ || R ₃ ) =8,33 Ω

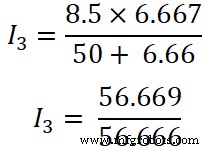
Ik ₂ =2,499 ≈ 2,5 A

Nu passen we de stroomdelerregel toe op de derde weerstand (50 Ω), en de stroom die door deze weerstand gaat is I₃ .

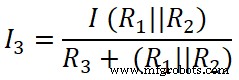
Hier,

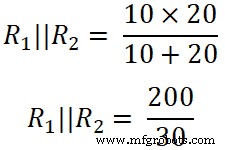
(R ₁ || R ₂ ) =6.66 Ω

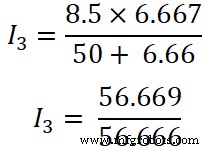
Ik ₃ =1,00 A

Dus de som van alle drie de stromen is;

Ik ₁ + Ik ₂ + Ik ₃ =5 + 2,5 + 1 =8,5 A

En deze stroom is gelijk aan de totale stroom geleverd door de bron.

Huidige duikerregel voor AC-circuit

Voorbeeld-2

Beschouw een wisselstroomcircuit met een parallel geschakelde weerstand en condensator, zoals weergegeven in de onderstaande afbeelding. Zoek de stroom die door de weerstand en condensator gaat met behulp van de huidige delerregel. Houd rekening met een frequentie van 60 Hz.

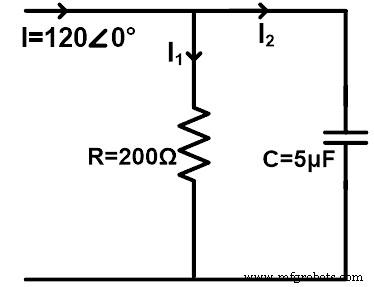
Z_R =200 Ω =200∠0°Ω

Z_C =1/(2 πf C) =1/(2 π 60(5×10 ⁶ ) )

Z_C =10 ⁶ / (600 π)

Z_C =530,78 ∠-90° Ω

Volgens de huidige delerregel is de stroomvergelijking die door de weerstand gaat;

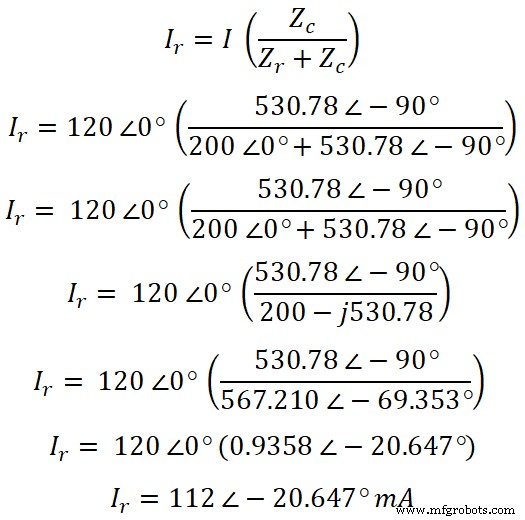
Nu kunnen we op dezelfde manier de stroom door de condensator vinden. Volgens de stroomdelerregel is de stroomvergelijking die door de condensator gaat;

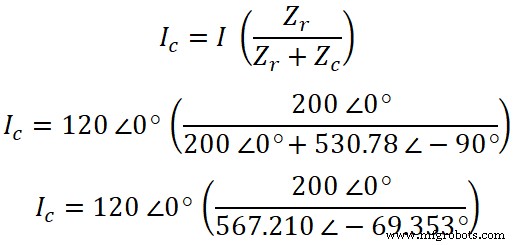
I_C =120 ∠0° (0,3526 ∠ 69,353°)

I_C =42,31 ∠ 69,353°

Als je dit antwoord wilt bewijzen, kun je beide stromen toevoegen. En de waarde van deze stroom is hetzelfde als de bronstroom.

Verwante handleidingen voor analyse van elektrische circuits:

• Compensatiestelling – Bewijs, uitleg en opgeloste voorbeelden
• Substitutiestelling – Stapsgewijze handleiding met opgelost voorbeeld
• SUPERNODE-circuitanalyse - stap voor stap met opgelost voorbeeld
• SUPERMESH-circuitanalyse - stap voor stap met opgelost voorbeeld
• Kirchhoff's stroom- en spanningswet (KCL &KVL) | Opgelost voorbeeld
• Cramer's Rule Calculator - 2 en 3 vergelijkingssysteem voor elektrische circuits
• Wheatstone Bridge – Circuit, werking, afleiding en toepassingen
• Elektrische en elektronische technische rekenmachines
• 5000+ elektrische en elektronische technische formules en vergelijkingen