Vertakking huidige methode

De eerste en meest rechttoe rechtaan netwerkanalysetechniek heet de Branch Current Method . Bij deze methode gaan we uit van richtingen van stromen in een netwerk en schrijven vervolgens vergelijkingen die hun relaties met elkaar beschrijven via de wetten van Kirchhoff en Ohm. Zodra we één vergelijking hebben voor elke onbekende stroom, kunnen we de gelijktijdige vergelijkingen oplossen en alle stromen bepalen, en dus alle spanningsdalingen in het netwerk.

Oplossen met de vertakkingsstroommethode

Laten we dit circuit gebruiken om de methode te illustreren:

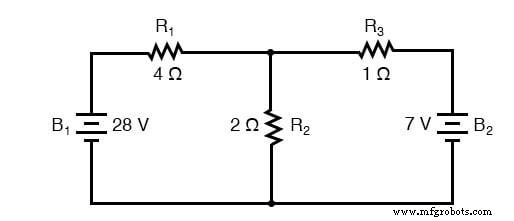
Een knooppunt kiezen

De eerste stap is het kiezen van een knooppunt (kruispunt van draden) in het circuit om te gebruiken als referentiepunt voor onze onbekende stromen. Ik kies het knooppunt rechts van R₁ , de bovenkant van R₂ , en de linkerkant van R₃ .

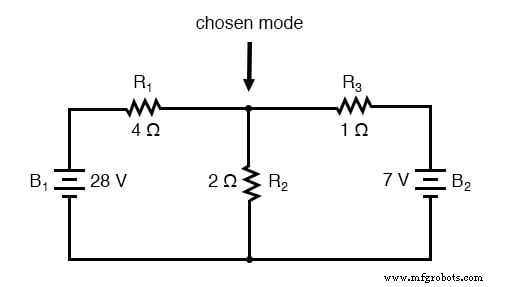
Raad bij dit knooppunt in welke richting de stromen van de drie draden gaan, en label de drie stromen als I₁ , ik₂ , en ik₃ , respectievelijk. Houd er rekening mee dat deze stroomrichtingen op dit moment speculatief zijn. Gelukkig, als blijkt dat een van onze gissingen verkeerd was, zullen we weten wanneer we de stromen wiskundig oplossen (elke "verkeerde" stroomrichtingen zullen als negatieve getallen in onze oplossing verschijnen).

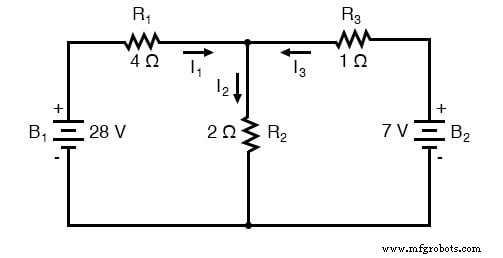
Pas de huidige wet van Kirchhoff (KCL) toe

De stroomwet van Kirchhoff (KCL) vertelt ons dat de algebraïsche som van stromen die een knoop binnenkomen en verlaten gelijk moet zijn aan nul, dus we kunnen deze drie stromen relateren (I₁ , ik₂ , en ik₃ ) aan elkaar in een enkele vergelijking. Omwille van de conventie, zal ik elke huidige invoer aanduiden het knooppunt als positief in teken, en alle huidige verlaten de knoop als negatief in teken:

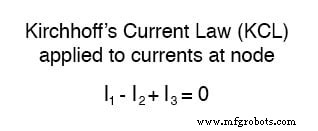
Label alle spanningsdalingen

De volgende stap is om alle spanningsvalpolariteiten over weerstanden te labelen volgens de veronderstelde richtingen van de stromen. De polariteit is positief waar de stroom de weerstand binnenkomt en negatief waar het de weerstand verlaat:

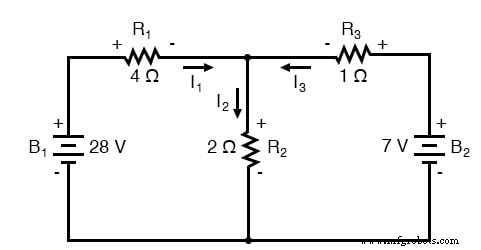
De batterijpolariteiten blijven natuurlijk zoals ze waren volgens hun symboliek (korte einde negatief, lange einde positief). Het is OK als de polariteit van de spanningsval van een weerstand niet overeenkomt met de polariteit van de dichtstbijzijnde batterij, zolang de polariteit van de weerstandsspanning correct is gebaseerd op de veronderstelde stroomrichting erdoorheen. In sommige gevallen kunnen we ontdekken dat de stroom terug wordt gedwongen door een batterij, waardoor dit effect ontstaat. Het belangrijkste om hier te onthouden is om al uw weerstandspolariteiten en daaropvolgende berekeningen te baseren op de richtingen van de stroom (en) die aanvankelijk werd aangenomen. Zoals eerder vermeld, als je aanname niet klopt, zal dit duidelijk worden zodra de vergelijkingen zijn opgelost (door middel van een negatieve oplossing). De omvang van de oplossing zal echter nog steeds correct zijn.

Pas de spanningswet van Kirchhoff (KVL) toe

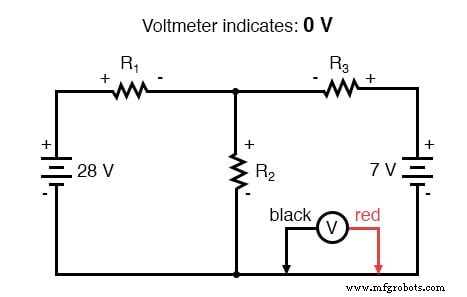
De spanningswet van Kirchhoff (KVL) vertelt ons dat de algebraïsche som van alle spanningen in een lus gelijk moet zijn aan nul, dus we kunnen meer vergelijkingen maken met huidige termen (I₁ , ik₂ , en ik₃ ) voor onze gelijktijdige vergelijkingen. Om een ​​KVL-vergelijking te verkrijgen, moeten we spanningsdalingen in een lus van het circuit optellen, alsof we met een echte voltmeter meten. Ik kies ervoor om eerst de linkerlus van dit circuit te volgen, beginnend vanuit de linkerbovenhoek en tegen de klok in bewegend (de keuze van startpunten en richtingen is willekeurig). Het resultaat ziet er als volgt uit:

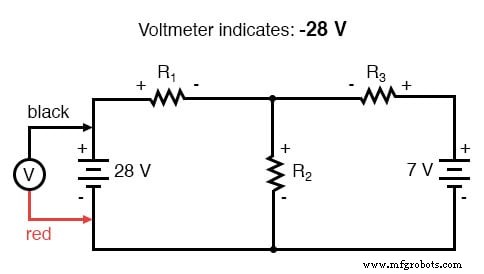
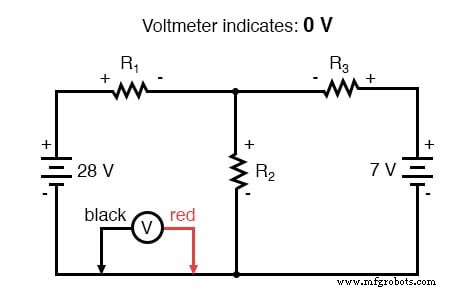
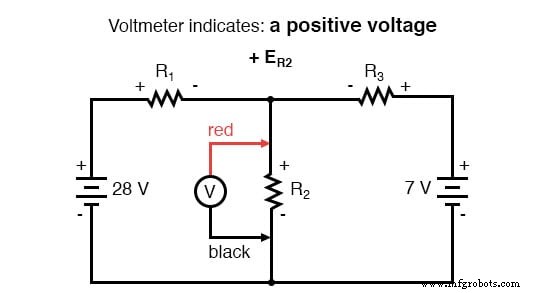
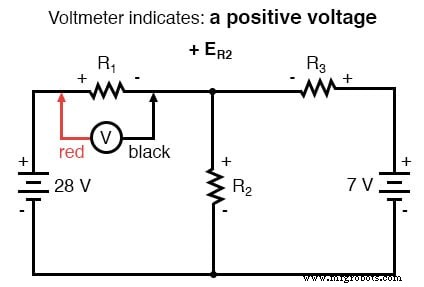
Nadat we ons spoor van de linkerlus hebben voltooid, voegen we deze spanningsindicaties samen voor een som van nul:

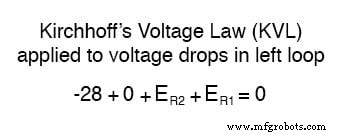
We weten natuurlijk nog niet wat de spanning is over R₁ of R₂ , dus we kunnen die waarden op dit moment niet als numerieke cijfers in de vergelijking invoegen. We doen echter weet dat alle drie de spanningen algebraïsch moeten optellen tot nul, dus de vergelijking is waar. We kunnen nog een stap verder gaan en de onbekende spanningen uitdrukken als het product van de corresponderende onbekende stromen (I₁ en ik₂ ) en hun respectievelijke weerstanden, volgens de wet van Ohm (E =IR), en elimineer de 0-termen:

Omdat we weten wat de waarden van alle weerstanden in ohm zijn, kunnen we die cijfers gewoon in de vergelijking vervangen om de zaken een beetje te vereenvoudigen:

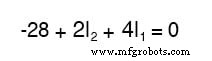
Je vraagt ​​je misschien af ​​waarom we zoveel moeite hebben gedaan om deze vergelijking te manipuleren vanuit zijn oorspronkelijke vorm (-28 + E_R2 + E_R1 ). De laatste twee termen zijn immers nog onbekend, dus welk voordeel heeft het om ze uit te drukken in onbekende spanningen of als onbekende stromen (vermenigvuldigd met weerstanden)? Het doel hiervan is om de KVL-vergelijking uitgedrukt te krijgen met behulp van dezelfde onbekende variabelen als de KCL-vergelijking, want dit is een noodzakelijke vereiste voor elke gelijktijdige methode voor het oplossen van vergelijkingen. Om drie onbekende stromen op te lossen (I₁ , ik₂ , en ik₃ ), moeten we drie vergelijkingen hebben met betrekking tot deze drie stromen (niet spanningen !) samen.

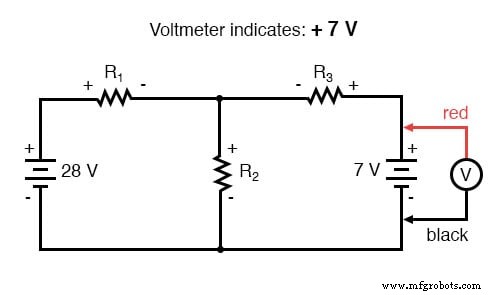
Door dezelfde stappen toe te passen op de rechter lus van het circuit (beginnend bij het gekozen knooppunt en tegen de klok in bewegend), krijgen we een andere KVL-vergelijking:

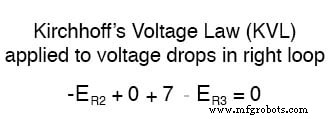
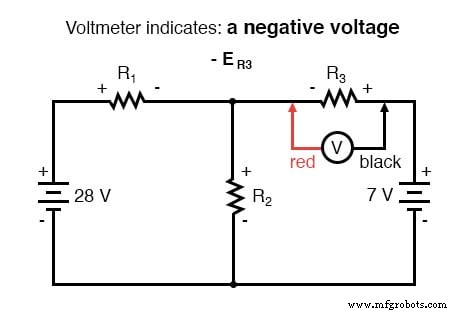
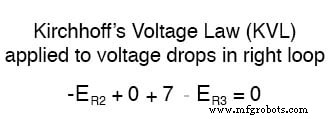
Nu we weten dat de spanning over elke weerstand kan en zou moeten zijn uitgedrukt als het product van de overeenkomstige stroom en de (bekende) weerstand van elke weerstand, kunnen we de vergelijking als zodanig herschrijven:

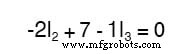
Oplossen voor het onbekende

Nu hebben we een wiskundig systeem van drie vergelijkingen (één KCL-vergelijking en twee KVL-vergelijkingen) en drie onbekenden:

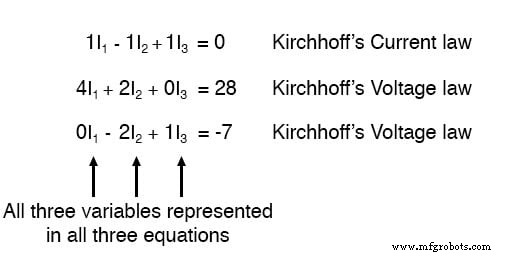
Voor sommige oplossingsmethoden (met name elke methode waarbij een rekenmachine betrokken is), is het handig om elke onbekende term in elke vergelijking uit te drukken, met een constante waarde rechts van het gelijkteken, en met alle "eenheids"-termen uitgedrukt met een expliciete coëfficiënt van 1. Als we de vergelijkingen opnieuw schrijven, hebben we:

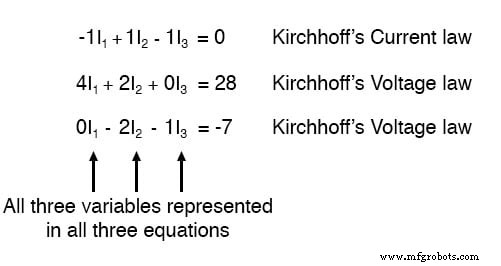
Met behulp van welke oplossingstechnieken dan ook die ons ter beschikking staan, zouden we tot een oplossing moeten komen voor de drie onbekende stroomwaarden:

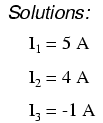
Dus ik₁ is 5 ampère, I₂ is 4 ampère, en ik₃ is een negatieve 1 amp. Maar wat betekent "negatieve" stroom? In dit geval betekent dit dat onze aangenomen richting voor I₃ was het tegenovergestelde van zijn echte richting. Als we teruggaan naar ons oorspronkelijke circuit, kunnen we de huidige pijl opnieuw tekenen voor I₃ (en herteken de polariteit van R₃ 's spanningsdaling om overeen te komen):

Het circuit opnieuw tekenen

Merk op hoe de stroom achteruit wordt geduwd door batterij 2 (elektronen stromen "naar boven") vanwege de hogere spanning van batterij 1 (waarvan de stroom "naar beneden" is gericht zoals normaal)! Ondanks het feit dat de polariteit van batterij B2 probeert om elektronen in die tak van het circuit naar beneden te duwen, worden elektronen er doorheen gedwongen vanwege de superieure spanning van batterij B1. Betekent dit dat de sterkere batterij altijd zal "winnen" en dat de zwakkere batterij er altijd stroom achterwaarts doorheen wordt gedwongen? Nee! Het hangt eigenlijk af van zowel de relatieve spanningen van de batterijen en de weerstandswaarden in het circuit. De enige zekere manier om te bepalen wat er aan de hand is, is door de tijd te nemen om het netwerk wiskundig te analyseren.

Bereken de spanningsval over alle weerstanden

Nu we de grootte van alle stromen in dit circuit kennen, kunnen we spanningsdalingen over alle weerstanden berekenen met de wet van Ohm (E=IR):

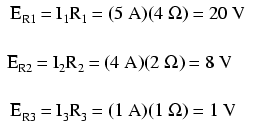
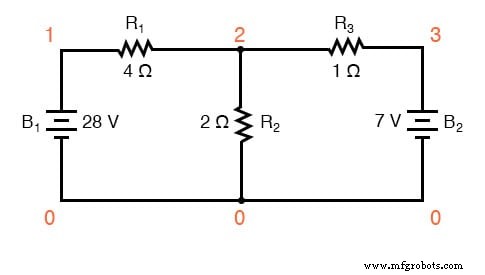
Netwerk analyseren met SPICE

Laten we dit netwerk nu analyseren met SPICE om onze spanningscijfers te verifiëren. We zouden de stroom ook kunnen analyseren met SPICE, maar omdat daarvoor extra componenten in het circuit moeten worden toegevoegd, en omdat we weten dat als de spanningen allemaal hetzelfde zijn en alle weerstanden hetzelfde, de stromen moeten em> allemaal hetzelfde zijn, kies ik voor de minder complexe analyse. Hier is een hertekening van ons circuit, compleet met knooppuntnummers waar SPICE naar kan verwijzen:

voorbeeld netwerkanalyse v1 1 0 v2 3 0 dc 7 r1 1 2 4 r2 2 0 2 r3 2 3 1 .dc v1 28 28 1 .print dc v(1,2) v(2,0) v(2,3) .einde v1 v(1,2) v(2) v(2,3) 2.800E+01 2.000E+01 8.000E+00 1.000E+00 

En ja hoor, de spanningscijfers blijken allemaal hetzelfde te zijn:20 volt over R₁ (knooppunten 1 en 2), 8 volt over R₂ (knooppunten 2 en 0), en 1 volt over R₃ (knooppunten 2 en 3). Let op de tekens van al deze spanningscijfers:het zijn allemaal positieve waarden! SPICE baseert zijn polariteiten op de volgorde waarin knooppunten worden vermeld, waarbij het eerste knooppunt positief is en het tweede knooppunt negatief. Een cijfer van positieve (+) 20 volt tussen knooppunten 1 en 2 betekent bijvoorbeeld dat knooppunt 1 positief is ten opzichte van knooppunt 2. Als het cijfer negatief was uitgekomen in de SPICE-analyse, hadden we geweten dat onze werkelijke polariteit was “achteruit” (knooppunt 1 negatief ten opzichte van knooppunt 2). Als we de knooppuntvolgorde in de SPICE-lijst controleren, kunnen we zien dat de polariteiten allemaal overeenkomen met wat we hebben bepaald met de Branch Current-analysemethode.

BEOORDELING:

• Te volgen stappen voor de analysemethode "Branch Current":
  • Kies een knoop en neem de richtingen van stromingen aan.
  • Schrijf een KCL-vergelijking met betrekking tot stromen op het knooppunt.
  • Label weerstandsspanningsvalpolariteiten op basis van veronderstelde stromen.
  • Schrijf KVL-vergelijkingen voor elke lus van het circuit en vervang het product IR voor E in elke weerstandsterm van de vergelijkingen.
  • Oplossen voor onbekende takstromen (gelijktijdige vergelijkingen).
  • Als een oplossing negatief is, dan is de aangenomen stroomrichting voor die oplossing verkeerd!
  • Oplossen voor spanningsdalingen over alle weerstanden (E=IR).

GERELATEERD WERKBLAD:

• Werkblad Stroomanalyse DC-tak