Effect van door machinale bewerking veroorzaakte ondergronddefecten op dislocatie-evolutie en mechanische eigenschappen van materialen via nano-inspringing
Abstract
Ondergrondse defecten hebben een aanzienlijke invloed op de precisie en prestaties van nanostructuren. In dit artikel wordt moleculaire dynamica-simulatie van nano-inspringing uitgevoerd om het effect van door machinale bewerking geïnduceerde ondergrondse defecten op dislocatie-evolutie en mechanische eigenschappen van materialen te onderzoeken, waarbij het specimenmodel met ondergrondse defecten wordt geconstrueerd door nano-cutting in overeenstemming met de werkelijkheid. Het vormingsmechanisme van ondergrondse defecten en het interactiemechanisme tussen machine-geïnduceerde defecten en dislocatie-evolutie worden besproken. De hardheid en de elasticiteitsmodulus van Young van eenkristalkoperspecimens worden berekend. De simulatieresultaten geven aan dat er stabiele defectstructuurresiduen bestaan in de ondergrond van het werkstuk, zoals atomaire clusters, tetraëdrische stapelfouten en dislocaties van trapstangen. Secundaire verwerking van nano-indrukking kan interne defecten van het werkstuk herstellen, maar de ondergrondse schade in het secundaire verwerkingsgebied wordt verergerd. De nano-indentatiehardheid van specimens neemt toe met de introductie van ondergrondse defecten, wat resulteert in de vorming van een werkverhardend effect. Het bestaan van ondergrondse defecten kan het vermogen van materiaal om elastische vervorming te weerstaan verzwakken, waarbij de onderlinge evolutie tussen dislocaties en ondergrondse defecten een belangrijke rol speelt.
Achtergrond
Ultraprecisie fabricage op nanometrische schaal wordt algemeen beschouwd als een effectieve methode om nanocomponenten te verkrijgen met submicron dimensionale nauwkeurigheid en nanoschaal oppervlaktekwaliteit [1]. Enkele stabiele ondergronddefecten blijven na fabricage in het werkstuk achter [2,3,4,5]. De ondergrondse defecten hebben niet alleen invloed op de verwerkingsnauwkeurigheid en oppervlaktekwaliteit, maar hebben ook een kritische invloed op de mechanische eigenschappen en levensduur van nanocomponenten. Veel onderzoeken naar ondergrondse defecten zijn uitgevoerd met behulp van de moleculaire dynamica (MD) -methode, voornamelijk gericht op de vorming en evolutie van ondergrondse defecten [6, 7], de dikte van de ondergrondse defecten (SSD) laag [8, 9] en de invloed van ondergronddefecten op de integriteit van het oppervlak [10, 11]. Het effect van ondergronddefecten op mechanische eigenschappen van werkstukmaterialen is echter minder bestudeerd. De mechanische eigenschappen van nanostructuren zijn van cruciaal belang voor hun serviceprestaties en levensduur. Daarom is het effect van ondergrondse defecten op mechanische eigenschappen van materialen de belangrijkste kwesties geworden die moeten worden onderzocht.
Er zijn veel onderzoeken uitgevoerd om de SSD-laag te beraadslagen door moleculaire dynamica-simulatie van het nano-snijproces. Narayanan [12] bestudeerde de vorming van stapelfout-tetraëdrische (SFT) in eenkristalgoud en introduceerde het door vervorming geïnduceerde mechanisme van SFT. Inamura [13] onderzocht de chipvorming en materiaalslipvervorming tijdens het nanosnijproces en wees erop dat de chipvorming voornamelijk wordt veroorzaakt door schuifslipvervorming. Pei [14] bestudeerde het effect van snijparameters op dislocatie-evolutie en snijkracht tijdens het nano-snijproces en ontdekte dat wanneer het werkstuk groter is dan 40 nm, het grootte-effect niet significant is. Dai [15] en Liu [16] gebruikten respectievelijk MD-simulatie- en experimentmethoden om de invloed van de structuur van diamantgereedschap en het grootte-effect op de evolutie van defecten onder het werkstuk te bestuderen. De eerdere studies tonen aan dat er stabiele ondergrondse defecten in het werkstuk bestaan na nano-cutting. Snijparameters en gereedschapsgeometrieparameters hebben grote invloeden op de dikte en evolutie van de ondergrondse schadelaag, en zelfs op de verwerkingsnauwkeurigheid. De mechanische eigenschappen van werkstukmaterialen kunnen echter niet worden berekend door de relevante gegevens te analyseren die zijn verkregen door nanosnijden.
Nano-inspringing is een effectieve techniek om de mechanische eigenschappen zoals hardheid en elasticiteitsmodulus [17] te karakteriseren. Er zijn veel onderzoeken uitgevoerd naar nano-inspringing om de prestaties van mechanische eigenschappen te evalueren door experimentele en theoretische modellen. Zimmerman [18] analyseerde de dislocatie-emissie in het nano-indentatieproces door de slipvector. Ruestes [19] bestudeerde nano-indentatie van monokristal Fe door middel van MD-simulatie en ontdekte dat het genereren van dislocaties in de ondergrond noodzakelijk is om het materiaal uit de indentatiezone te verwijderen. Huang [20] voerde MD-simulaties uit van nano-inspringing op eenkristal-diamantmatrix en ontdekte dat de vervorming van diamantmateriaal onder inkeping werd gedomineerd door de kiemvorming en voortplanting van 〈110〉 {111} dislocatielussen. Sharma [21] construeerde kunstmatig een model van harde deeltjes in kopermatrix en analyseerde de invloed van harde deeltjes op de evolutie van ondergrondse defecten in het bewerkingsproces. Peng [22] onderzocht de versterkingsmechanismen van grafeencoatings op Cu-substraat door nano-indentatie, wat het gevolg is van het stresshomogenisatie-effect dat door het grensvlak wordt gegenereerd. Uit de bovenstaande analyse blijkt dat de eerdere onderzoeken naar het effect van ondergrondse defecten voornamelijk gebaseerd zijn op perfecte kristalmaterialen of kunstmatige constructie van hypothetische defecten, wat ver verwijderd is van de werkelijke ondergrondse defecten. Daarom is het realistisch construeren van het werkstukmodel met ondergrondse defecten essentieel om de invloed van ondergrondse defecten op mechanische eigenschappen van het werkstuk te analyseren.
In dit artikel werd de nano-snijmethode toegepast om het werkstukmodel te verkrijgen met ondergrondse defecten in overeenstemming met praktische kenmerken. Op basis hiervan werd nano-indentatiesimulatie uitgevoerd om het effect van ondergrondse defecten op de mechanische eigenschappen van monokristalkoper te bestuderen. Ten eerste zal het vormings- en evolutiemechanisme van ondergrondse defecten tijdens het nano-snijproces worden besproken, en zullen de typische defectstructuren van de ondergrond van het werkstuk na nano-cutting worden geanalyseerd. Ten tweede zal het interactiemechanisme tussen door machinale bewerking veroorzaakte ondergrondse defecten en dislocatie-nucleatie tijdens indentatie worden geanalyseerd. Ten derde, op basis van de belasting-verplaatsingsgegevens verkregen door nano-indentatie, zullen de hardheid en de elasticiteitsmodulus van Young van eenkristalkoperspecimens worden berekend. Ten slotte zullen enkele nieuwe conclusies worden samengevat.
Methoden
Simulatiemodel
Om het effect van ondergrondse defecten op mechanische eigenschappen van materialen bij nanobewerking te onderzoeken, moet het modelmodel met ondergrondse defecten worden geconstrueerd. In dit onderzoek wordt dit gerealiseerd door MD-simulatie van het nanosnijproces. Allereerst wordt het MD-simulatiemodel opgesteld en wordt de simulatie van het nanosnijproces uitgevoerd. Vervolgens ontspanden het preparaat en het snijgereedschap gedurende voldoende tijd tijdens MD-simulatie . Ten slotte bleven er enkele stabiele defecten in de ondergrond van werkstuk. Het schematische diagram van de driedimensionale MD-simulatiemodellen wordt getoond in Fig. 1, waarin het nano-snijmodel wordt getoond in Fig. 1a en het nano-indentatiemodel met ondergrondse defecten wordt getoond in Fig. 1b. In Fig. 1 zijn de materialen van het werkstuk en het monster eenkristalkoper en het gereedschap en het indenter zijn diamantmaterialen. Het diamantgereedschap met boogblad wordt gebruikt in het nano-snijproces en de straal van de gereedschapsrand is 3 nm. De indringer heeft een halve bolvorm in het nano-indentatieproces en de diameter is 6 nm. Het werkstuk en het monster zijn verdeeld in drie delen, respectievelijk Newton-laag, temperatuurlaag en grenslaag. Om het grootte-effect en het grenseffect te verminderen, wordt de periodieke randvoorwaarde (PBC) aangenomen in de richting van [010] van het simulatiesysteem. Om de initiële interactie tussen gereedschap en werkstuk te voorkomen, wordt het snijgereedschap 3 nm rechtsboven op het werkstuk geplaatst en wordt de indringer 6 nm tot aan het preparaat geplaatst. De gedetailleerde simulatieparameters worden getoond in Tabel 1.
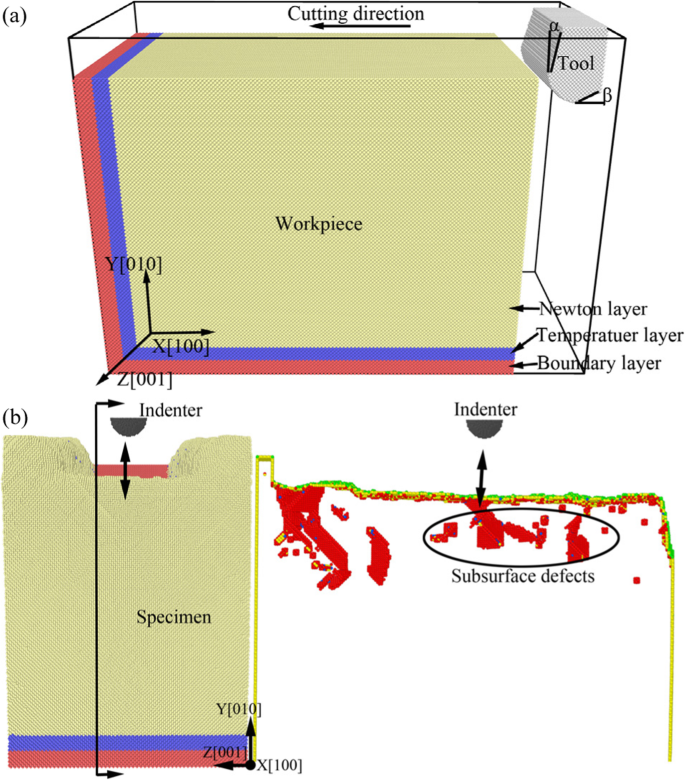
Schematisch diagram van 3-D MD-simulatiemodellen van eenkristalkoper voor nano-cutting en nano-indentation. een Het model voor het nano-snijproces. b Het model voor nano-indrukkingsproces met ondergrondse defecten
Interatomaire potentiële functies
In dit onderzoek werden de driedimensionale MD-simulaties uitgevoerd door een grootschalige atomaire/moleculaire massaal parallelle simulator (LAMMPS). De parallelle berekening werd gerealiseerd met behulp van een interfacebibliotheek voor het doorgeven van berichten. De Morse-potentiaal, Embedded-atom Method (EAM)-potentiaal en Tersoff-potentiaal worden gebruikt in de simulatie, die worden aangeroepen vanuit het LAMMPS-softwarepakket. De interactie tussen Cu-atomen in het werkstuk en C-atomen in het gereedschap wordt berekend door Morse-potentiaal die wordt weergegeven in Vgl. 1 [23].
$$ u\left({r}_{ij}\right)=D\left[\exp \left(-2\alpha \left({r}_{ij}-{r}_0\right)\right )-2\exp \left(-\alpha \left({r}_{ij}-{r}_0\right)\right)\right] $$ (1)waar r 0 , α , en D respectievelijk zijn atomaire afstand, elasticiteitsmodulus en bindingsenergie. De waarde wordt weergegeven in Tabel 2.
De interatomaire functie tussen Cu-atomen in het werkstuk wordt beschreven door EAM-potentiaal die wordt weergegeven in Vgl. 2, 3 [24, 25].
$$ E=\sum \limits_i^N\left[F\left({\rho}_i\right)+\sum \limits_{j>i}^Nu\left({r}_{ij}\right) \right] $$ (2) $$ {\rho}_i=\sum \limits_jf\left({r}_{ij}\right) $$ (3)De interactie tussen koolstofatomen in diamantgereedschap wordt berekend door Tersoff-potentiaal die wordt weergegeven in vergelijkingen. 4, 5 [26].
$$ E=\frac{1}{2}\sum \limits_{i\ne j}{V}_{ij} $$ (4) $$ {V}_{ij}={f}_c\left ({r}_{ij}\right)\left[{V}_R^{\hbox{'}}\left({r}_{ij}\right)+{b}_{ij}{V} _A\links({r}_{ij}\rechts)\rechts] $$ (5)waar f c (r ij ) is de afknotfunctie tussen atomen, V A (r ij ) is de dubbele potentiaal van de absorptieterm, V R (r ij ) is de dubbele potentiaal van afstoting term, en r ij is atomaire afstand tussen atoom i en atoom j .
Defectanalysemethoden
Bij het nanosnijden van monokristallijn koper worden vervormingen en dislocaties gevormd onder de oppervlakte van het werkstuk. In dit artikel wordt de centrosymmetrieparameter (CSP) geïntroduceerd om de dislocatiekiemvorming en defectevolutie van werkstukken te analyseren. Voor face center cubic (FCC) materialen kan de CSP-waarde worden berekend door Vgl. 6 [27].
$$ CSP=\sum \limits_{i=1}^6{\left|{R}_i+{R}_{i+6}\right|}^2 $$ (6)waar R ik is even lang als naburige atomen en R i+6 is de tegenovergestelde richting van naburige atomen. De CSP-waarden van FCC-kristal, gedeeltelijke dislocatie, stapelfout en oppervlakte-atomen zijn respectievelijk 0, 2.1, 8.3 en 24.9 [27].
De CSP-methode kan de atomaire versprongen identificeren, maar kan de lokale atomaire kristalstructuurstatus van het werkstuk niet herkennen. Daarom wordt de gemeenschappelijke buuranalyse (CNA) geïntroduceerd om het lokale kristalstructuurdefect te identificeren. In de originele CNA-methode, voorgesteld door Honeycutt en Andersen [28], worden de verschillende structuren weergegeven door diagrammen. Momenteel zijn er vijf soorten CNA-patronen in OVITO [29], waarbij de lokale kristalstructuren worden geïdentificeerd als face center cubic (FCC), close-packed hexagonal (HCP), body centred cubic (BCC), icosohedral (ICO), respectievelijk onbekend. In dit artikel wordt ook het dislocatie-extractalgoritme (DXA) [30] geïntroduceerd om de evolutie van dislocatiedefecten te analyseren. Door DXA worden de verschillende kristalstructuren in het werkstuk gemarkeerd met verschillende kleuren en worden de dislocatiedefecten in het werkstuk weergegeven door lijnen van verschillende kleuren.
Resultaten en discussie
Evolutie van ondergronddefecten in het nanosnijproces
In het nanosnijproces, onder de extrusie- en afschuifwerking van het snijgereedschap op het werkstuk, wordt het werkstukoppervlakmateriaal met de dikte van de snijdiepte verwijderd en wordt een nieuw machinaal bewerkt oppervlak met een bepaalde maatnauwkeurigheid en oppervlaktekwaliteit gevormd. De complexe elastisch-plastische vervorming, inclusief spanningsvervorming en thermische vervorming, vindt plaats in het oppervlak en de ondergrond van het werkstuk, samen met de energietransformatie en de spanningsconcentratie. Daarom wordt de ondergrondse schadelaag gevormd en wordt de chip verwijderd. Figuur 2 toont de onmiddellijke weergaven van de evolutie van het ondergrondse defect en de materiaalverwijdering tijdens het nanosnijproces van eenkristalkoper. In Fig. 2 worden de atomen gekleurd door de waarde van de CSP- en CNA-analyseresultaten. In Fig. 2a en c zijn de gele, groene, rode en blauwe atomen oppervlakte-atomen, oppervlaktedefecten-atomen, ondergrondse defect-atomen en FCC-atomen. Uit figuur 2 blijkt dat tijdens het nanosnijproces een groot aantal typische defectstructuren in de ondergrond van het werkstuk worden gevormd, zoals puntdefecten, leegstanddefecten, stapelfouten, clusterdefecten, prismatische dislocaties en schroefdislocatielus.
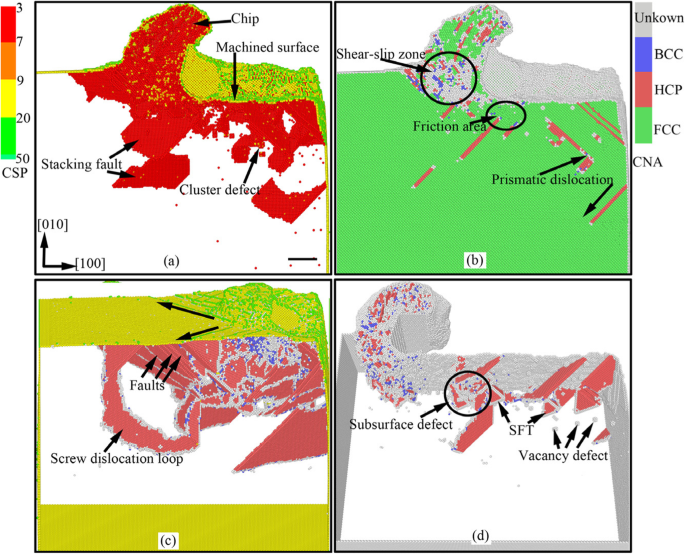
Direct zicht op de evolutie van het ondergrondse defect tijdens het nanosnijproces van eenkristalkoper (kleur online, schaalbalk 5 nm). De snijafstanden van a , b , c , en d respectievelijk zijn 18 nm, 18 nm, 6 nm en 32 nm
Vanwege het knijp- en schuifeffect van het snijgereedschap, wordt de schuifslipvervorming gegenereerd voor de atomen voor het harkvlak en wordt de primaire schuifslipzone gevormd in het werkstuk tijdens het nano-snijproces, zoals weergegeven in Fig. 2b. Sommige van deze atomen glijden langs het harkvlak omhoog en de snijchip wordt gevormd zoals weergegeven in figuur 2a. Sommige bewegen naar beneden en het bewerkte oppervlak wordt gevormd onder de knijpwrijving van het flankvlak van het gereedschap, zoals weergegeven in figuur 2b. Anderen gaan naar binnen en de ondergrondse defecten worden gevormd, zoals stapelfouten, clusterdefecten en prismatische dislocaties, getoond in Fig. 2a en b.
Vanwege de wrijving en extrusie van het flankoppervlak van het gereedschap, vindt de energieaccumulatie plaats voor atomen in de buurt van het flankvlak en worden de atomen in hoogenergetische atomen. Wanneer de atoomenergie een bepaald niveau overschrijdt, zal de energie die wordt gedragen door energetische atomen worden vrijgegeven en de dislocatie wordt gevormd onder de energetische atomen die aandrijven. Daarom worden er veel dislocaties gevormd in het wrijvingsgebied van het flankvlak, weergegeven in figuur 2d. Terwijl het machinaal bewerkte oppervlak wordt gevormd, kiemen, breiden en vernietigen dislocaties zich onder het oppervlak. Ten slotte blijven de defectstructuren zoals stapelfouten, SFT en leegstanddefecten in de ondergrond, zoals aangegeven in figuur 2d. De stapelfouten worden genucleëerd in de afschuifslipzone onder het snijgereedschap, vervolgens uitgebreid in het werkstuk en uiteindelijk vernietigd op het vrije oppervlak van het werkstuk. Uiteindelijk wordt de dislocatielijn gevormd op het werkstukoppervlak. En de dislocatielijn wordt verlengd langs \( \left[\overline{1}0\overline{1}\right] \), \( \left[\overline{1}01\right] \), en [101] routebeschrijving. De schroefdislocatielus, die zich aan de rand van de schuifslipzone bevindt, bestaat uit verschillende stapelfouten en een reeks schroefdislocaties. De dislocatie van de schroef wordt gevormd onder het aandrijven van de compressiespanningstoestand van de schuifslipzone [11].
In het nano-snijproces worden de dislocaties genucleëerd en verlengd onder invloed van het snijgereedschap. Samen met de aggregatie en afgifte van energie, fluctueert de snijkracht met de toename van de snijafstand, die in Fig. 3 in drie dimensies wordt getoond. In Fig. 3 zijn de zwarte, rode en blauwe curven respectievelijk de voedingskracht (Fx), de tegenkracht (Fy) en de tangentiële kracht (Fz). Uit figuur 3 blijkt dat het snijproces is verdeeld in twee perioden, namelijk de initiële snijfase en de stabiele snijfase. Tijdens de eerste snijfase nemen de voedingskracht en de tegenkracht snel rechtlijnig toe. De maximale waarde van de voedingskracht is meer dan 1100 nN bereikt, maar de tegenkracht is net aangekomen rond de 600 nN. Wanneer de gereedschapspunt volledig in het werkstuk snijdt, wordt het bewerkte oppervlak gevormd, weergegeven als de eerste kleine grafiek ondertekend als Machinaal oppervlak in Fig. 3. Vervolgens wordt het nano-snijproces overgebracht naar een stabiele snijfase. In de stabiele snijfase fluctueren alle drie de krachten in hun evenwichtsposities. De gemiddelde voedingskracht is ongeveer 1000 nN en de gemiddelde tegenkracht is slechts ongeveer 500 nN. Uit Fig. 3 blijkt dat de voedingskracht snel afneemt bij de snijafstand van 20 nm. Het is omdat de energieaccumulatie op een bepaald niveau is aangekomen, namelijk de kritische roosterspanningsenergie, weergegeven als de tweede kleine grafiek in Fig. 3. Ondertussen wordt er een grote weerstand uitgeoefend op het snijgereedschap, waardoor de snijkracht wordt een piekwaarde. Dan komt de energie vrij die resulteert in de dislocatie-emissie, en de snijkracht wordt verminderd, weergegeven als de derde kleine grafiek in Fig. 3. Daarom fluctueert de snijkracht tijdens de stabiele snijfase. De kiemvorming, uitbreiding en vernietiging van dislocaties leidden tot de fluctuatie van de snijkracht en resulteerden uiteindelijk in het ondergrondse defect in het werkstuk.
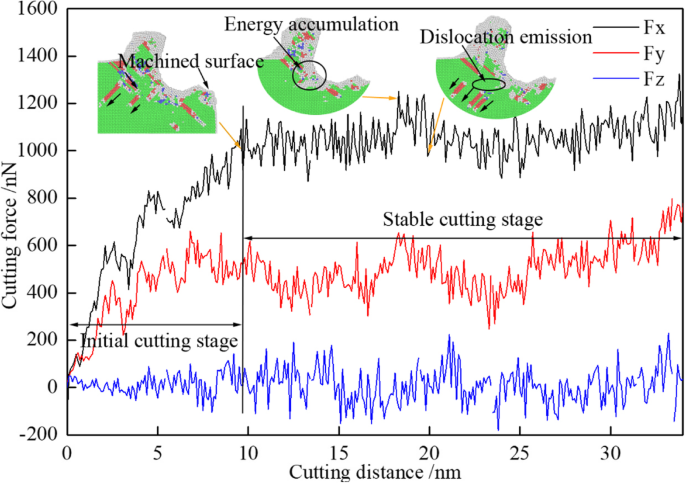
De variatiecurve van de snijkracht met de snijafstand (kleur online). De zwarte, rode en blauwe curven zijn respectievelijk de voedingskracht (Fx), de tegenkracht (Fy) en de tangentiële kracht (Fz)
Om de evolutie en emotie van dislocatiedefecten in de ondergrond van het werkstuk tijdens het nano-snijproces gedetailleerd te onderzoeken, worden de dislocatieverdeling en de variatie ervan met de snijafstand minutieus geanalyseerd met de CNA-methode. De evolutie van het ondergronddefect van het werkstuk op een bepaald gebied wordt getoond in Fig. 4, waarin de snijafstanden van Fig. 4a, b, c, d, e en f respectievelijk 8 nm, 10 nm, 12 nm, 20 nm zijn , 24 nm en 32 nm. Uit Fig. 4a kan worden gezien dat veel dislocatiedefecten worden genucleëerd in de afschuifslipzone onder de extrusie-afschuifwerking van het snijgereedschap tijdens de voorbereidende fase van het snijproces. In het bijzonder worden een V-vormige dislocatie en een fout gevormd onder de aandrijvende werking van atomaire spanning en energie in de afschuifslipzone, getoond in figuur 4b. In het daaropvolgende bewerkingsproces wordt de schuif-slipzone naar voren bewogen terwijl het snijgereedschap in beweging blijft. Omdat de vervormingsenergie afneemt, wordt de fout geleidelijk vernietigd. Terwijl het snijgereedschap naar voren blijft bewegen, wordt de wrijvingszone van het flankvlak in de buurt van de fout bewogen. En het met ruwheid bewerkte oppervlak wordt gevormd onder de extrusie en wrijving van het flankvlak. Vervolgens wordt de fout verder vernietigd en geleidelijk losgemaakt van het werkstukoppervlak, zoals weergegeven in figuur 4d. Ten slotte wordt de fout omgezet in een clusterdefect dat gestaag aanwezig is in de ondergrond van het werkstuk. Evenzo wordt de gevormde V-vormige dislocatie geleidelijk geëvolueerd tot SFT onder de interactie van twee stapelfouten en een dislocatievergrendeling. Deze stabiele defecten vormen samen de ondergrondse vervormde laag, zoals weergegeven in Fig. 4e en Fig. 4f.

Ondergrondse defecten evolutie van het werkstuk (kleur online). De snijafstanden van a , b , c , d , e , en f respectievelijk 8 nm, 10 nm, 12 nm, 20 nm, 24 nm en 32 nm
Zoals we weten, zal de resterende spanningsafgifte en herstel van interne defecten plaatsvinden op het werkstuk na verouderingsbehandeling. Bij daadwerkelijke nanofabricage zullen sommige van de tijdens de verwerking gevormde ondergrondse defecten na het bewerkingsproces verdwijnen. Om de toestand van het werkstuk na verouderingsbehandeling te simuleren, wordt gedurende lange tijd moleculaire dynamica-relaxatie op het snijsysteem uitgevoerd. Het distributiediagram van het resterende defect in de ondergrond van het werkstuk na MD-relaxatie gedurende lange tijd wordt getoond in Fig. 5, waarin de atomen worden gekleurd volgens de analyseresultaten door CSP- en CNA-methoden. Uit figuur 5 blijkt dat de primaire dislocaties na relaxatie worden vernietigd. De leegstandsdefecten, stapelfouten, atomaire cluster, prismatische dislocatie, schroefdislocatie, SFT en trapstangdislocatie komen voor in de ondergrond van het werkstuk, zoals weergegeven in Fig. 5. Volgens de bovenstaande analyse zijn deze defecten, die gevormd worden onder de inductie van complexe interne spanning en de interactie van dislocatiedefecten, zal de maatnauwkeurigheid en oppervlaktekwaliteit van het werkstuk beïnvloeden na nanobewerking.
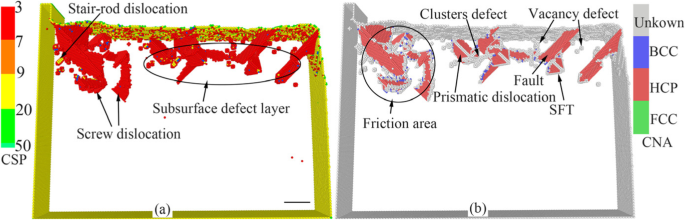
Verdeling van resterende defecten in de ondergrond van het werkstuk na nanometersnijden (kleur online, schaalbalk 5 nm). een De gele, groene, rode en blauwe atomen zijn oppervlakte-atomen, oppervlaktedefecten-atomen, ondergrondse defect-atomen en FCC-atomen. b De groene, rode, grijze en blauwe atomen zijn FCC, HCP, onbekend en BCC-structuur
Nano-indentatietest op koperspecimen met door machinale bewerking veroorzaakte ondergronddefecten
De door machinale bewerking veroorzaakte restdefecten van de ondergrond bepalen de mechanische eigenschappen van het oppervlak, met name de hardheid en Young's modulus. Daarom lijkt het onderzoek naar de nucleatie en interactie van dislocaties tijdens nano-indentatie dringend noodzakelijk. Om de invloed van de door machinale bewerking veroorzaakte ondergrondse defecten op de mechanische eigenschappen van eenkristalkoper te onderzoeken, werd het nano-indentatieproces op het monster na nano-cut in de praktijk gebracht met dezelfde parameters als nano-cutting simulatie. Het simulatieresultaat wordt getoond in Fig. 6, 7, 8, 9 en 10. Het momentane atomaire beeld van de distributie van ondergrondse defecten in de begintoestand van nano-inspringing wordt getoond in Fig. 6. Uit de figuur blijkt dat er verschillende SFT's zijn, een V-vormige dislocatie, enkele prismatische dislocaties en enkele clusterdefecten onder het indenter. Deze ondergrondse defecten kunnen de dislocatiekiemvorming en uitzetting van het werkstuk tijdens het nano-indentatieproces beïnvloeden. En dan worden de mechanische eigenschappen van het werkstukmateriaal veranderd.
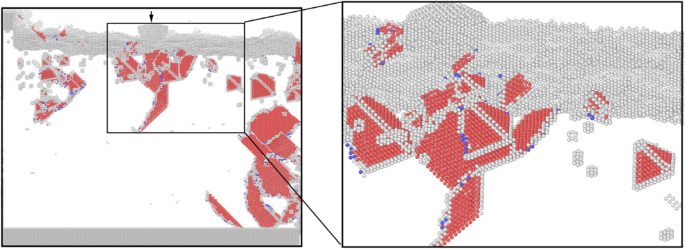
Ondergrondse defecten verdeling van het werkstuk in de eerste indruktoestand (kleur online). De rode, grijze en blauwe atomen zijn HCP, onbekend en BCC-structuur
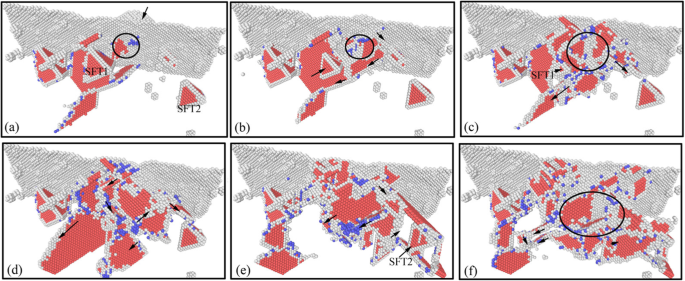
Ondergrondse dislocatiedefecten evolutie in laadproces van nano-inspringing (kleur online). De corresponderende inspringdieptes van a –f zijn respectievelijk 0 nm, 0,5 nm, 1 nm, 2 nm, 3 nm en 4 nm
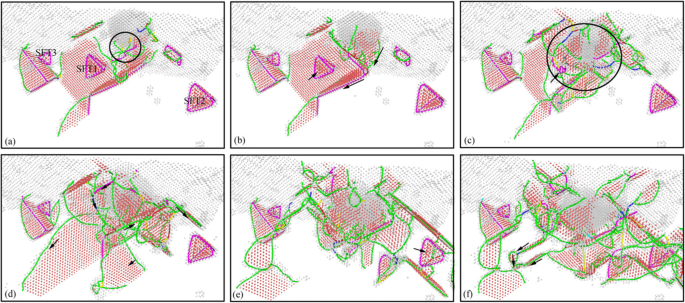
Verdeling van ondergrondse dislocaties in het laadproces van nano-inspringing (kleur online). De corresponderende inspringdieptes van a –f zijn respectievelijk 0 nm, 0,5 nm, 1 nm, 2 nm, 3 nm en 4 nm. Kleurenschema:diepblauw voor perfecte dislocaties, groen voor Shockley-dislocaties, roze voor Stair-rod dislocaties, geel voor Hirth-dislocaties, lichtblauw voor Frank-dislocaties en rood voor niet-geïdentificeerde dislocaties
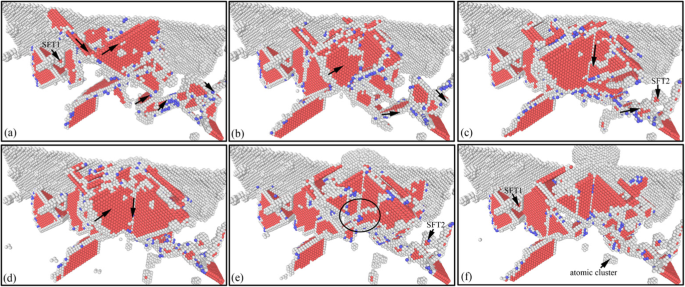
Ondergrondse defecten evolutie in losproces van nano-inspringing (kleur online). De corresponderende inspringdieptes van a –f zijn respectievelijk 4 nm, 3 nm, 2 nm, 1 nm, 0 nm en − 1 nm
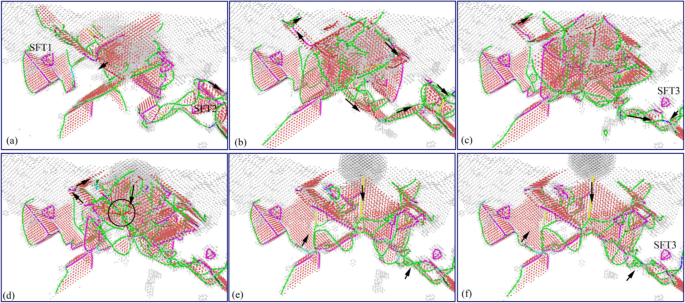
Verdeling van ondergrondse dislocaties in het losproces van nano-inspringing (kleur online). De corresponderende inspringdieptes van a –f zijn respectievelijk 4 nm, 3 nm, 2 nm, 1 nm, 0 nm en − 1 nm. Kleurenschema:diepblauw voor perfecte dislocaties, groen voor Shockley-dislocaties, roze voor Stair-rod dislocaties, geel voor Hirth-dislocaties, lichtblauw voor Frank-dislocaties en rood voor niet-geïdentificeerde dislocaties
Het atomaire evolutiebeeld van ondergrondse dislocaties tijdens het laadproces van nano-indentatie wordt getoond in figuur 7. In figuur 7a is te zien dat de initiële kiemvorming van dislocatie plaatsvindt op het oppervlak van het monster wanneer het indenter contact maakt met het oppervlak van de exemplaar. Met de neerwaartse druk van de indenter worden de genucleëerde dislocaties geleidelijk uitgebreid. Ondertussen, onder invloed van de spanning uitgeoefend door de indringer, ontstonden een groot aantal dislocaties en bewogen ze langs het slipsysteem, zoals weergegeven in figuur 7b. Onder de interactie tussen nieuw gevormde dislocaties en originele ondergrondse defecten, verdwijnen enkele eenvoudige defecten geleidelijk, en de V-vormige dislocaties blijven zich ontwikkelen en geleidelijk vernietigen. De SFT onder de indenter wordt geleidelijk verlaagd, zoals weergegeven in figuur 7c. Naarmate het indentatieproces vordert, neemt de schaal van nieuwe genucleëerde dislocatiedefecten toe en verdwijnen de V-vormige dislocatie en SFT1 onder indenter geleidelijk. Tegelijkertijd worden de dislocatiedefecten gevormd tijdens het inspringen geleidelijk geëvolueerd tot een prismatische dislocatielus, waarin stapelfouten geleidelijk verdwijnen, zoals weergegeven in figuur 7d. De nieuw gevormde prismatische dislocatielus blijft zich uitbreiden tot SFT2 rechtsonder in de indenter. Vanwege zijn stabiele structuur blijft de SFT2 onvervormd tijdens de expansie van de prismatische dislocatielus, zoals weergegeven in figuur 7e. Terwijl de indenter naar beneden drukt, blijft de prismatische dislocatielus zich naar beneden uitbreiden en neemt de schaal van de dislocatiedefecten in het ondergrondse gebied geleidelijk toe. De SFT2-structuur is stabiel aanwezig in de ondergrond van het monster en heeft geen verandering tijdens de beweging en interferentie van de dislocatiedefecten, zoals weergegeven in Fig. 7 f.
Om de evolutie en verdeling van ondergrondse defecten tijdens het inkepingsproces duidelijker te laten zien, wordt de DXA-methode gebruikt om het monster na inkeping te analyseren. Het beeld van de dislocatiedislocatie onder het oppervlak op elk moment dat overeenkomt met Fig. 7 wordt verkregen door DXA-analyse, zoals weergegeven in Fig. 8. Dislocaties worden gekleurd op basis van het volgende schema:diepblauw voor perfecte dislocaties, groen voor Shockley-dislocaties, roze voor Stair-rod dislocaties, geel voor Hirth-dislocaties, lichtblauw voor Frank-dislocaties en rood voor niet-geïdentificeerde dislocaties.
Uit Fig. 8 blijkt dat de ondergrond van het werkstuk voornamelijk bestaat uit Shockley-dislocatie en Stair-rod dislocatie in de initiële inkepingstoestand. De SFT die in de ondergrond bestond, is een regelmatige tetraëdrische structuur die bestaat uit zes dislocaties van trapstangen. Wanneer de indenter contact maakt met het werkstuk, is de dislocatiekiemvorming op het werkstukoppervlak gele Hirsh-dislocaties, zoals weergegeven in Fig. 8a. Terwijl de indenter naar beneden drukt, wordt een groot aantal dislocaties gevormd en verplaatst langs het slipsysteem. De gele Hirsh-dislocaties veranderen geleidelijk in groene Shockley-dislocaties, zoals weergegeven in figuur 8b. Onder de interactie tussen nieuw gevormde dislocaties en de originele SFT1 verdwijnen enkele eenvoudige dislocaties geleidelijk, zoals weergegeven in figuur 8c. De schaal van ondergrondse dislocaties neemt toe naarmate de indenter naar beneden valt, en de nieuw gevormde dislocaties zijn voornamelijk groene Shackley-dislocaties. De interactie tussen Shockley-dislocaties en SFT1 resulteert in de grootte van de SFT1 geleidelijke afname en uiteindelijke verdwijning van SFT1, zoals weergegeven in figuur 8d. Met de toename van de schaal van defecten, nemen het aantal en de soorten dislocaties in de ondergrond van het monster toe. Er zijn rode onbekende soorten dislocaties gevormd in de ondergrond, en verschillende Shockley-dislocaties vormden de prismadislocatielus, zoals weergegeven in figuur 8e. Onder de interactie van de Shockley-dislocatie en de Stair-rod dislocatie, verdwenen de SFT2 en SFT3 ver van het inkepingsgebied uiteindelijk niet, vanwege de zwakkere extrusie van de indenter, zoals weergegeven in Fig. 8f.
Het evolutiebeeld van ondergrondse dislocatie tijdens het lossen van nano-indentatie wordt getoond in Fig. 9. Figuur 10 toont het distributiebeeld van ondergrondse dislocatie corresponderend in Fig. 9. Uit de twee grafieken blijkt dat de schaal van ondergrondse defecten toeneemt eerst, en dan geleidelijk afneemt tijdens het proces van het naar boven bewegen van de indenter. Het wordt veroorzaakt door de uitgebreide functie tussen continue afgifte van de materiaalvervormingsenergie en de adhesiekracht die door de indenter op het monster wordt uitgeoefend. In de beginfase van het losproces is de opwaartse adsorptiekracht van het indentereffect op het monster niet significant. De evolutie van ondergrondse defecten wordt voornamelijk aangedreven door de materiaalvervormingsenergie, wat resulteert in een toename van de omvang van ondergrondse defecten. En de belangrijkste soorten dislocaties in het podium zijn de groene Shockley-dislocatie en de roze ladderdislocatie, zoals weergegeven in Fig. 9a, b en 10a, b. De interactie tussen de SFT2 en Shockley-dislocatie in de buurt zorgt ervoor dat roze trapstangdislocatie verandert in groene Shackley-dislocatie in het gebied ver weg indenteractie. Ondertussen wordt de SFT2 omgezet in een kleiner defect dat SFT3 is, zoals getoond in Fig. 9c en 10c. Met het continu optillen van de indringer, neemt het bindende en adsorberende effect dat door de indringer op het monster wordt uitgeoefend geleidelijk toe. Accompany with the deformation energy release, the size and types of dislocations in subsurface increase. And more perfect dislocations, Hirh dislocations, and unknown dislocations are formed, as shown in Figs. 9d and 10d. In later stage of unloading process, the material deformation energy is basically released, and the evolution of subsurface defects is dominated by the adsorption from the indenter. Therefore, the subsurface defects are annihilated rapidly, and the scale of subsurface defects decreases rapidly. And a typical Hirsch dislocation is formed in the direction of the indenter upward, which is shown in Figs. 9e, f and 10e, f. Finally, the scale of subsurface defects decreases considerably, and some typical subsurface defects, such as SFT and atomic clusters, are gradually disappeared. From the above analysis, it can be seen that secondary processing (nano-indentation) can restore the typical internal defects formed in nano-cutting, and the subsurface damage becomes more serious in the secondary processing area. These characteristics of subsurface defects will affect the mechanical properties of materials. Hence, it is necessary to study the effect of subsurface defects on the mechanical properties of material.
Mechanical properties of materials can be calculated by load-displacement curve, such as hardness, elastic modulus, and yield strength. In this study, hardness and Young’s modulus of single crystal copper were investigated. The variation of load on the indenter was monitored during the nano-indentation process, and the load-displacement curve of the nano-indentation process was drawn, as shown in Fig. 11. The max indentation depth of the red and black curves respectively is 2 nm and 3 nm, in which both loading and unloading processes are included. The upward direction of load is defined as positive direction, so the load-displacement curves are all above the zero line in the process of loading, while the load on the indenter changes from positive to negative during unloading. The elasticity restore of deformed matrix material exerts an upward force on the indenter. Therefore, in order to keep the indenter raising in uniform speed, a downward force (positive) is required. With the gradual recovery of deformation, the force gradually decreases until it disappears. Then the force applied on the indenter becomes negative, and the absolute value of the force first increases and then decreases. From the graph, it can be seen that the specimen is in the stage of elastic deformation during loading process, and the load increases in proportion to the displacement. When the displacement of the indenter is 1 nm, the load on the indenter is fluctuated dramatically, as indicated by the arrow on the left side of Fig. 11. This is because that the indenter is pressed down to the SFT1 shown in Fig. 7, which results in the greater impediment to the indenter. When the indenter displacement is in the range of 2 to 3 nm, the fluctuation amplitude of the load increases. This is because the indenter is pressed down to the SSD layer, and the impediment of the indenter to the subsurface defect in the specimen is more significant, so the fluctuation amplitude of the load increases significantly.
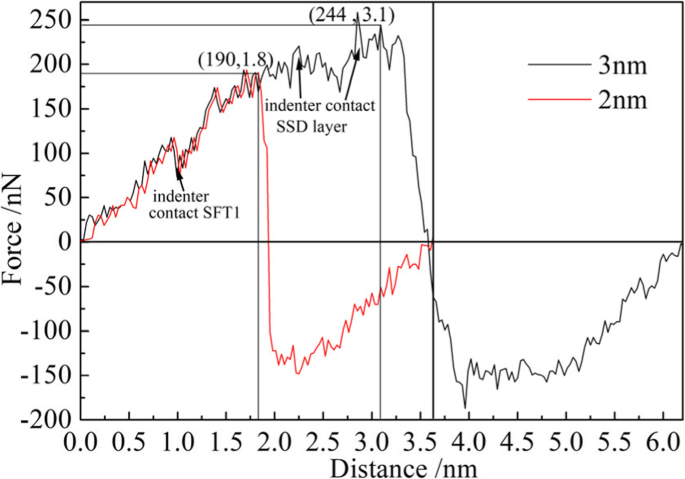
Load-displacement curve of nano-indentation on the machining-induced specimen (color online). The maximum indentation depth of the black curve and the red curve respectively is 3 nm and 2 nm
According to Oliver-Pharr Method [31], nano-indentation hardness can be defined as indentation load divided by the contact area between indenter and specimen, which is calculated by Eq. 7.
$$ H={F}_{\mathrm{max}}/{A}_c $$ (7)In which, F max is the peak value of the load. A c is projected contact area for indenter and specimen, which can be obtained by
$$ {A}_c=\pi {r}^2 $$ (8)waar r is contact radius for indenter. Because the indenter is hemispherical in shape, r is approximately equal to indentation depth.
The elastic deformation of single crystal copper material is caused by the load exerted from indenter. Based on the previous load-displacement curve, Young’s modulus (E ) of single crystal copper can be calculated by Eq. 9.
$$ E=\frac{\sigma }{\varepsilon }=\frac{F/S}{DL/L}=\frac{F/\pi {r}^2}{DL/L} $$ (9)waar F is applied load, S is contact area, r is projection radius of indenter, DL is material deformation along loading direction, which is equal to indentation depth, and L is the total length of material along loading direction. In this study, L is equal to 30 nm.
According to the Oliver-Pharr method and load-displacement data, nano-indentation hardness and Young’s elastic modulus of single crystal copper materials with subsurface defects can be calculated based on Eqs. 7, 8, 9. Table 3 shows the applied load acting on the specimens by indenter with different indentation depths.
The nano-indentation hardness of single crystal copper can be calculated by Eqs. 7 and 8 combining the data in Table 3. When the maximum depth is 2 nm, F max =190.67 nN and from Fig. 11 r =2.75 nm. The calculated value of nano-indentation hardness H2 is 8.029 GPa. When the maximum depth is 3 nm, F max =244.66 nN and r =3 nm. The calculated value of nano-indentation hardness H3 is 8.675 GPa, which is slightly larger than it obtained at indentation depth of 2 nm. It is because the indenter is pressed down to the subsurface defects area at indentation depth of 3 nm, and the deformation resistance of the subsurface defects increases. Therefore, the hardness of the single crystal copper increased. It can be concluded from the result that the subsurface defects make the machined surface much harder, which is work-hardening phenomenon.
The Young’s modulus E of single crystal copper can be calculated by Eq. 9 combining the data in the Table 3. The calculation results are shown in Table 4. It can be noted that the Young’s modulus becomes distinctly higher when the indentation depth is smaller than 1.5 nm. In the initial stage of nano-indentation, the indenter does not contact the defects residual area in subsurface. However, the work-hardening effect makes the specimen material not easily be occurred elastic deformation; therefore, the Young’s modulus of single crystal copper is larger in the initial stage of indentation. The value of Young’s modulus is 119.4 GPa when indentation depth is 2 nm, which is almost the same with Zhang’s research (120.4 GPa) [14]. With the increase of indentation depth, the Young’s elastic modulus of single crystal copper specimens decreases gradually, and the ability of materials to resist elastic deformation is weakened. It is due to the permanent elastic deformation is derived from the dislocation motion and its interaction with subsurface defects. It has been revealed that the nano-cutting-induced subsurface defects will affect the physical and mechanical properties of single crystal copper materials, which is also applicable to other FCC materials. The existence of subsurface defects will enhance the hardness of machined surface and weaken the ability of material to resist elastic deformation, in which the mutual evolution between dislocations and subsurface defects plays an important role. Therefore, it is very important to predict the thickness of subsurface deformation layer and study the surface properties for nano-fabrication.
Conclusies
The subsurface defects stable exist in workpiece after nano-cutting can affect the mechanical properties, which is critical to the service performance and life of nano-structures. The previous studies are mainly based on perfect crystal materials or artificial constructing hypothetical defects, which is far from the actual subsurface defects. In this paper, molecular dynamics simulation of nano-cutting is performed to construct the specimen model with subsurface defects. Based on the built MD model, nano-indentation simulation is carried out to study the influence of machining-induced subsurface defects on the physical and mechanical properties of single crystal copper materials. The interaction mechanism between dislocation and complex defects during nano-indentation is studied. The nano-indentation hardness and Young’s elastic modulus of single crystal copper materials are calculated. Based on the above analysis, some interesting conclusions can be drawn as follows.
- 1.
The dislocation nucleation and expansion in workpiece subsurface are driven by the extrusion and shearing action of cutting tool during the nano-cutting process, which results in the fluctuation of cutting force. After nano-cutting, there are stable defect structure residues in the subsurface of workpiece, such as vacancy defects, stacking faults, atomic clusters, SFT, and stair-rod dislocations, which together constitute the subsurface defect layer of workpiece.
- 2.
The existence of subsurface defects affects the nucleation and expansion of dislocations during nano-indentation process. Some stable defects directly below the indenter, such as V-shaped dislocation and SFT1, are annihilated after indentation. And SFT2 far from the indentation region is transformed into a smaller one. Secondary processing of nano-indentation can restore typical internal defects of the workpiece, but the subsurface defects in the secondary processing area are aggravated.
- 3.
The nano-indentation hardness of specimens increases with the introduction of subsurface defects, which results in the formation of work-hardening effect. The Young’s modulus of single crystal copper is larger in the initial stage of indentation and gradually decreases with the increase of indentation depth. The existence of subsurface defects can weaken the ability of material to resist elastic deformation, in which the mutual evolution between dislocations and subsurface defects plays an important role.
Beschikbaarheid van gegevens en materialen
The conclusions made in this manuscript are based on the data which are all presented and shown in this paper.
Afkortingen
- MD:
-
Moleculaire dynamiek
- SSD:
-
Subsurface defects
- SFT:
-
Stacking fault tetrahedral
- PBC:
-
Periodic boundary condition
- LAMMPS:
-
Grootschalige atomaire/moleculaire massaal parallelle simulator
- EAM:
-
Embedded-atom method
- CSP:
-
Centro-symmetry parameter
- FCC:
-
Face center cubic
- CNA:
-
Common neighbor analysis
- HCP:
-
Close-packed hexagonal
- BCC:
-
Lichaam gecentreerd kubisch
- ICO:
-
Icosohedral
- DXA:
-
Dislocation extract algorithm
Nanomaterialen
- De evolutie van de markt voor 3D-printmaterialen:trends en kansen in 2019
- De evolutie van SLS:nieuwe technologieën, materialen en toepassingen
- Hoe beoordelen ingenieurs plastic materialen en materiaalsterkte?
- Nanogestructureerde Silica/Gold-Cellulose-Bonded Amino-POSS Hybrid Composite via Sol-Gel Process en zijn eigenschappen
- Het effect van contactloos plasma op structurele en magnetische eigenschappen van Mn Х Fe3 − X О4 Spinels
- Paramagnetische eigenschappen van van fullereen afgeleide nanomaterialen en hun polymeercomposieten:drastisch uitpompeffect
- Synergetisch effect van grafeen en MWCNT's op microstructuur en mechanische eigenschappen van Cu/Ti3SiC2/C nanocomposieten
- Eigenschappen van technische materialen:algemeen, fysiek en mechanisch
- Lijst met 14 verschillende mechanische eigenschappen van materialen
- Eigenschappen van staalmaterialen en gereedschappen die worden gebruikt voor ponsen
- Verschillende soorten materiaal mechanische eigenschappen



