Nano-meting van gesolvateerde biomoleculen of nanodeeltjes uit de zelfdiffusiviteit van water in bio-geïnspireerde nanoporiën
Abstract
Geïnspireerd door de structuur van diatomeeënalgen en gemotiveerd door de behoefte aan nieuwe detectiestrategieën voor opkomende nanoverontreinigingen in water, analyseren we het potentieel van nanoporeuze silicatabletten als meetapparatuur voor de concentratie van biomoleculen of nanodeeltjes in water. Het concept is gebaseerd op het verschillende diffusiegedrag dat watermoleculen vertonen in bulk en nano-ingesloten omstandigheden, bijvoorbeeld in nanoporiën. In deze laatste situatie neemt de zelfdiffusiecoëfficiënt van water af volgens de geometrie en oppervlakte-eigenschappen van de porie en de concentratie van gesuspendeerde biomoleculen of nanodeeltjes in de porie, zoals uitgebreid aangetoond in een eerdere studie. Dus, voor een bepaald porie-vloeistofsysteem, biedt de zelfdiffusiviteit van water in nanoporiën gevuld met biomoleculen of nanodeeltjes een indirecte maat voor hun concentratie. Met behulp van moleculaire dynamica en eerdere resultaten uit de literatuur, demonstreren we de correlatie tussen de zelfdiffusiecoëfficiënt van water in nanoporiën van silica en de concentratie van eiwitten of nanodeeltjes daarin. Ten slotte schatten we de tijd die de nanodeeltjes nodig hebben om de nanoporiën te vullen, om de praktische haalbaarheid van het algemene nanometingsprotocol te beoordelen. De resultaten laten zien dat de voorgestelde aanpak een alternatieve methode kan zijn om de concentratie van sommige klassen nanoverontreinigende stoffen of biomoleculen in water te beoordelen.
Achtergrond
De behoefte aan technieken voor het monitoren van de waterkwaliteit heeft een antieke oorsprong [1]. In het oude Rome werden waterbronnen vaak verontreinigd door biologische verontreinigende stoffen van dode lichamen van mensen en dieren of afvalwater van baden, en door niet-biologische verontreinigende stoffen zoals lood [2], wat ernstige ziekten en mentale problemen veroorzaakte. Voortdurend onderzoek en vooruitgang door de eeuwen heen stellen het grootste deel van de wereldbevolking tegenwoordig in staat toegang te hebben tot veilig drinkbaar kraanwater; toch hebben nog steeds meer dan 850 miljoen mensen geen primaire toegang tot schoon water [3].
Nauwkeurige kwaliteitsbewaking is een uitdagende taak, vanwege de verschillende aard van de verontreinigende stoffen die water kunnen verontreinigen, vaak in lage concentraties. Met name een aanzienlijk aantal opkomende verontreinigende stoffen op sporenniveau, bijv. farmaceutische producten, chemicaliën of nanomaterialen, worden niet vaak gecontroleerd en verwijderd door bestaande waterzuiveringsinstallaties [4], hoewel ze nadelige effecten kunnen hebben op het milieu en de menselijke gezondheid [5].
In de afgelopen decennia heeft de komst van nanotechnologieën het mogelijk gemaakt om op maat gemaakte moleculaire sensoren te ontwerpen om verschillende verontreinigende stoffen in water te detecteren, zoals pathogenen, organische en anorganische chemicaliën [6]. In hun meest basale versie bestaan deze sensoren uit een nanogestructureerd materiaal, een parseerelement voor herkenning en een actief mechanisme om de verkregen informatie door te geven [7]. Als er geen kwantitatieve informatie wordt verkregen, worden deze systemen eerder nanosondes [8] genoemd en vertrouwen ze ook op een gefunctionaliseerd materiaal om selectief chemicaliën te detecteren.
Op biomedisch gebied is de detectie van biomoleculen in lage concentraties cruciaal om de nauwkeurigheid van diagnostiek te verbeteren en medische behandelingen en medicijnen af te stemmen op de behoeften van de patiënten. Voor dit doel zijn ultragevoelige identificatiemethoden ontwikkeld, gebaseerd op een breed scala aan fysische en chemische verschijnselen, om het detectiesignaal van laaggeconcentreerde biomoleculen te versterken [9-11].
In dit kader hebben nanoporeuze materialen veel aandacht gekregen vanwege hun bijzondere structuur, gekenmerkt door holtes en kanalen, waardoor ze bijzonder geschikt zijn voor een aantal nanotechnologische toepassingen, zoals katalyse [12], adsorptiewarmteopslag [13], moleculaire zeven [14], selectief transport (membranen) [15], nanomotion [16], medicijnafgifte [17] en biosorptie [18].
De natuur heeft de ontwikkeling van deze toepassingen enorm geïnspireerd, omdat het uitstekende voorbeelden biedt van efficiënte hiërarchisch poreuze structuren met specifieke functionaliteiten [19, 20]. In silico-optimalisatie en goed ontworpen synthese maken het mogelijk om mogelijke beperkingen te overwinnen, zoals lage stabiliteit en weinig weerstand tegen ruwe omgevingen voor de vereiste toepassingen [21, 22].
Geïnspireerd door het exoskelet (frustule) van diatomeeënalgen [23], conceptualiseren we in dit werk nanoporeuze meettabletten voor de concentratie van sommige klassen van biomoleculen en nanodeeltjes in water. Het belangrijkste idee is om te vertrouwen op de verschillende zelfdiffusiecoëfficiënten die watermoleculen vertonen in bulk- en nano-ingesloten omstandigheden, bijvoorbeeld in nanoporiën van silica. Wanneer ze inderdaad op nanoschaal zijn, hebben watermoleculen een verminderde mobiliteit en dus minder ruimte voor diffusie. De aanwezigheid van een moleculaire opgeloste stof, bijvoorbeeld nanodeeltjes of biomoleculen, vermindert de mobiliteit verder, afhankelijk van de grootte en aard ervan, naast de grootte en geometrie van de porie. Dit gedrag kan nauwkeurig worden hersteld door een schaalwet die eerder in de literatuur is geïntroduceerd [24], wat aantoont dat de zelfdiffusiecoëfficiënt van water in een nanoporie het mogelijk maakt om indirect de concentratie van biomoleculen of nanodeeltjes daarin te kwantificeren. Resultaten verkregen via moleculaire dynamica voor verschillende concentraties van eiwitten en ijzeroxide-nanodeeltjes in nanoporiën van silica laten zien dat het voorgestelde concept een duidelijk inzicht geeft in hun concentratie met bevredigende nauwkeurigheid.
Presentatie van de hypothese
Bio-geïnspireerd nanometerconcept
Diatomeeën zijn eencellige micro-organismen (eukaryote algen) die in alomtegenwoordige waterige omgevingen leven. Hun cellen zijn verdeeld in twee helften, ingesloten in een siliciumdioxide-omhulsel (frustule). Deze poreuze matrix (exoskelet) stelt de levende cellen in staat om te interageren met de externe omgeving, waardoor de hechting van nanodeeltjes en actieve biomoleculen via het hydrofiele oppervlak en de hoge oppervlakte-tot-volumeverhouding wordt geoptimaliseerd [23]. De nanoporiën en spleten van de poreuze matrix, samen met zijn chemische eigenschappen, kunnen worden gebruikt voor het bio-geïnspireerde ontwerp van een aantal nanotechnologische apparaten voor verschillende toepassingen [25].
Op basis van de structuur van diatomeeënalgen, conceptualiseren we hier nanometer-silicatabletten voor sommige klassen nanodeeltjes en biomoleculen in water. Figuur 1a toont een scanning elektronenmicroscopie van de centrische diatomee Thalassiosira pseudonana [26]. De klep bestaat uit een poreuze structuur die wordt gekenmerkt door kanalen waarvan de diameter in de orde van enkele nanometers ligt, in dit geval specifiek rond de 10 nm (zie een detailweergave in de inzet). Eén zo'n regelmatige poreuze structuur vertegenwoordigt een natuurlijke zeef voor moleculen die groter zijn dan de poriegrootte, maar het maakt het binnendringen van kleinere moleculen mogelijk, waardoor een beperkende omgeving ontstaat die kan worden benut voor ons nanometerconcept.
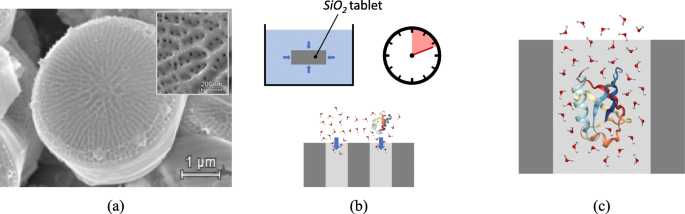
Bio-geïnspireerde conceptualisering van de nanometer-silicatabletten. een Scanning-elektronenmicroscopie van Thalassiosira pseudonana , met de hele klep en het detail van de poreuze nanokanalen in het inzetstuk. Afbeelding aangepast van [26] en gebruikt onder CC BY 4.0-licentie. b Uitgaande van de aanvankelijk lege nanoporiën, hebben de watermoleculen en gesolvateerde eiwitten de neiging om de silica-nanotabletten binnen te dringen met een karakteristieke vultijd. c Detail van het binnendringen van ubiquitine (1UBQ) in een silica-nanoporie, resulterend in verminderde mobiliteit van de watermoleculen als gevolg van de elektrostatische interacties met het eiwit en nanoporiën-oppervlakken
Als de diatomeeën poreuze structuur, of een soortgelijke verkregen via kunstmatige synthese [27], wordt ondergedompeld in een watermonster met gesuspendeerde verontreinigende stoffen, worden deze laatste gedreven door capillariteit en concentratiegradiënt in de poreuze kanalen, zie Fig. 1b, totdat evenwicht is bereikt. bereikt. In de nanoporiën hebben watermoleculen een verminderde mobiliteit vanwege de nano-opsluiting die wordt geboden door het oppervlak van de porie en binnengedrongen nanodeeltjes. Als gevolg hiervan neemt de zelfdiffusiecoëfficiënt van water in de nanoporie af ten opzichte van die van de bulk, zie figuur 1c. De kennis van deze laatste zelfdiffusiecoëfficiënt in de nanoporie, die bijvoorbeeld kan worden verkregen via diffusie magnetische resonantie beeldvorming (D-MRI) [28, 29] of quasi-elastische neutronenverstrooiing (QENS) technieken [30, 31 ], maakt het mogelijk om de concentratie van de verontreinigende stoffen af te leiden via de procedure die in de volgende sectie wordt uitgelegd.
Deeltjesconcentratie door zelfdiffusiviteit van water
In de nabijheid van vaste oppervlakken zijn watermoleculen onderhevig aan het effect van van der Waals- en Coulomb-interacties; dus vertonen ze ander gedrag met betrekking tot bulkomstandigheden [32, 33]. In het bijzonder veroorzaken die vast-vloeistof-interacties een gelaagdheid van de watermoleculen dicht bij het vaste oppervlak, wat hun mobiliteit vermindert en dus de zelfdiffusiecoëfficiënt met betrekking tot de bulkconditie.
Een schaalwet voor het voorspellen van de zelfdiffusiecoëfficiënt van water die dit effect omvat, is voorgesteld in de vorm [24]
$$\begin{array}{*{20}l} D =D_{B} \left[ 1 + \left(\frac{D_{C}}{D_{B}} - 1 \right) \theta \ rechts], \end{array} $$ (1)waar D B en D C zijn respectievelijk de zelfdiffusiecoëfficiënten van water in bulk en volledig nano-ingesloten omstandigheden. In verg. (1), θ is een schaalparameter die wordt beïnvloed door de geometrie en chemische eigenschappen van het vaste oppervlak, zijnde de verhouding tussen de nanobegrensde en totale watervolumes in de beschouwde configuratie, namelijk θ =V c /V tot . In het bijzonder, gegeven een bepaalde configuratie waar water nanobegrensd is, V c staat voor het volume water waarvan de mobiliteit aanzienlijk wordt veranderd door de interacties tussen vast en vloeibaar, en V tot het totale volume dat via het water bereikbaar is. Het nano-opgesloten watervolume V c kan worden gedefinieerd als de som van de i de voor oplosmiddelen toegankelijke oppervlakken S A S ik in het gegeven systeem maal een gemiddelde karakteristieke afstand \(\bar {\delta }_{i}\) waaronder de watermoleculen significant worden beïnvloed door de potentiaalput gegenereerd door de i het vaste oppervlak, namelijk:
$$\begin{array}{*{20}l} V_{\text{c}} =\sum_{i=1}^{N} \text{SAS}_{i} \, \bar{\delta }_{i} \,, \end{array} $$ (2)N . zijn het aantal verschillende vaste-vloeistof-interfaces in het systeem. De gemiddelde karakteristieke lengte van water nano-opsluiting uitgeoefend door een bepaald vast oppervlak \(\bar {\delta }_{i}\) kan gemakkelijk worden geschat op basis van atomistische simulaties, zodra de geometrische en chemische eigenschappen van het oppervlak bekend zijn [24, 34 ]. Merk op dat er een gedeeltelijke overlap van de nanoconfined watervolumes kan optreden als er meerdere vaste-vloeistof-interfaces aanwezig zijn, bijvoorbeeld in het geval van een nanoporie gevuld met nanodeeltjes. In dit geval is de schaalparameter θ in verg. (1) is slechts schijnbaar en kan waarden aannemen die groter zijn dan 1, waardoor de werkelijke fractie van nano-opgesloten water wordt overschat. Met dit effect kan rekening worden gehouden door continuümpercolatietheorie (CPT) [35], die de effectieve volumefractie als [24]
geeft $$\begin{array}{*{20}l} \theta^{*}=1 - \exp(-\theta). \end{array} $$ (3)Daarom kan een nauwkeurigere schatting van water nano-opsluiting in het geval van grote overlappingen tussen opsluitende volumes worden verkregen door θ ∗ , die daarom beter zou moeten worden gebruikt in Vgl. (1) in plaats van θ . Duidelijk, θ ∗ ≈θ voor θ →0.
Als het voor oplosmiddel toegankelijke oppervlak van een gesolvateerd nanodeeltje (of biomolecuul) gelijk is aan S A S ik , Verg. (2) kan worden gebruikt om het gemiddelde nano-opgesloten watervolume per nanodeeltje (of biomolecuul) te verkrijgen als \(V_{\text {c}_{\text {i}}}={SAS}_{i} \, \ staaf {\delta }_{i}\). Dit levert direct het aantal gesuspendeerde nanodeeltjes op als \(\phantom {\dot {i}\!}n_{i} =V_{\text {c}} / V_{\text {c}_{\text {i} }}\) en dus hun aantalconcentratie. Uiteindelijk kan de concentratie in termen van massa worden verkregen via de molaire massa van de beschouwde soort.
Vergelijking 1 is voor het eerst verkregen uit atomistische simulaties en gevalideerd tegen Magnetic Resonance Imaging (MRI) -experimenten [24]; achtereenvolgens is het ook gevalideerd door QENS-metingen [30, 31] en toegepast om verschillende eigenschappen van water op vaste-vloeistofgrensvlakken te interpreteren [32, 36].
Moleculaire dynamiek
Er worden simulaties uitgevoerd om de effectiviteit van Vgl. (1) om de nanodeeltjes- of biomolecuulconcentratie in een gehydrateerde nanoporie af te leiden, gezien de zelfdiffusiecoëfficiënt van water daarin. De open-source software GROMACS [37] wordt gebruikt voor de moleculaire dynamica (MD) simulaties. Om de verschillende mobiliteit van water in bulk- en nanobegrensde omstandigheden te analyseren, worden twee verschillende geometrische lay-outs geanalyseerd. Voor bulkcondities wordt een kubieke rekendoos gebruikt, waarbij periodiciteit wordt toegepast langs de drie Cartesiaanse assen. Voor nano-beperkte omstandigheden wordt een vereenvoudigde weergave van de porie in de nanometer-silicatabletten aangenomen, bestaande uit een enkele cilindrische nanoporie (zie figuur 1c). Omwille van de eenvoud, maar zonder verlies van algemeenheid, wordt uitgegaan van een regelmatige porievorm/grootteverdeling, en dus wordt periodiciteit toegepast langs de assen.
De geometriebestanden voor de beschouwde eiwitten (ubiquitine - 1UBQ; kippenei-wit lysozyme - 1AKI) werden verkregen uit de Protein Data Bank [38]-database, terwijl zowel de silica-nanoporiën als de magnetiet-nanodeeltjes beschikbaar waren uit een eerdere studie [24]. De intramoleculaire gebonden interacties in de silica nanoporiën en ijzeroxide nanodeeltjes worden gemodelleerd door harmonische rek en hoekpotentialen, zoals beschreven in [24]. Hun niet-gebonden interacties worden gemodelleerd door 12-6 Lennard-Jones en elektrostatische potentialen, zoals ook gerapporteerd in [24]. Gebonden en niet-gebonden interacties van de eiwitten zijn ontleend aan GROMOS96 43a2 [39]. Merk op dat tijdens de equilibratie alle bindingen in de eiwitten stijf worden gehouden met behulp van het LINCS (Linear Constraint Solver) algoritme [40]. Het SPC/E-watermodel [41] met star gebonden interacties wordt in alle gevallen toegepast, omdat het nauwkeurig de meest relevante eigenschappen van water bij kamertemperatuur [42] herstelt.
In zowel bulk- als nanoconfined-configuraties wordt het systeem eerst geminimaliseerd en gesolvateerd (waterdichtheid ongeveer gelijk aan 1,00 g/cm 3 ) en, voor eiwitten, de nettolading geneutraliseerd via ionentoevoeging. In detail worden chloride-ionen in de simulatiebox geïntroduceerd om de netto positieve lading van lysozym te neutraliseren, terwijl ubiquitine neutraal is en dus geen ionentoevoeging vereist. Vervolgens wordt het gehydrateerde systeem gedurende voldoende tijd tot zijn energieminimum ontspannen. De temperatuur van het systeem wordt vervolgens geëquilibreerd door een simulatie in het NVT-ensemble voor 100 ps (T =300 K, Nosé-Hoover thermostaat) om convergentie van potentiële energie in de gesimuleerde configuratie te bereiken (ongeveer ± 1% fluctuaties rond de evenwichtswaarde, zie Aanvullend bestand 1:Figuur S1c). Daarna worden bulkconfiguraties ook geëquilibreerd in het NPT-ensemble voor 100 ps (T =300 K, Nosé-Hoover thermostaat; p =1 bar, Parrinello-Rahman barostat) om convergentie van de waterdichtheid in de gesimuleerde opstellingen te bereiken (ongeveer ± 2% fluctuaties rond de evenwichtswaarde, zie aanvullend bestand 1:figuur S1a). De productierun wordt uiteindelijk uitgevoerd in het NVT-ensemble (T =300 K, Nosé-Hoover thermostaat). In alle gesimuleerde gevallen wordt de stationaire toestand geacht te zijn bereikt wanneer de zelfdiffusiecoëfficiënt, die elke 100 ps wordt geëvalueerd, neigt naar een asymptotische waarde (dwz ± 10% fluctuaties rond het voortschrijdend gemiddelde, zie aanvullend bestand 1:figuur S1b en D). Aangezien dit over het algemeen wordt bereikt na ≈ 500 ps voor de bulkconfiguraties of ≈ 1000 ps voor de nanoconfined-configuraties, worden de eerste voortgezet tot 1 ns, de laatste tot 2 ns om betere statistieken te hebben. In alle runs wordt het haasje-over-algoritme met tijdstap 0,001 ps gebruikt, terwijl een afsnijafstand van 1,2 nm wordt gebruikt voor de van der Waals-interacties en een Particle Mesh Ewald (PME)-methode voor de elektrostatische (maaswijdte 0,16 nm). Het voor oplosmiddel toegankelijke oppervlak van de vaste nano-objecten wordt verkregen uit de productierun en ingevoerd in een speciale routine (zie de aanvullende software in [24]), die, op basis van het aangenomen krachtveld, de gemiddelde karakteristieke lengte van nano-opsluiting berekent \ (\bar {\delta }_{i}\) per elke i de vast-vloeistof-interface in de opstelling.
De hypothese testen
Zelfdiffusie van water voor verschillende systemen
De geldigheid van de schaalwet in Vgl. (1) is eerst getest rekening houdend met zowel resultaten uit de literatuur (14 configuraties) als nieuwe simulaties (9 configuraties). In het bijzonder zijn de configuraties uit de literatuur gehydrateerde silica-nanoporiën met een diameter d P =8,13 of 11,04 nm (zie aanvullende tabel S1 in [24]); enige magnetiet nanodeeltjes met diameter d p =1,27 of 1,97 nm ondergedompeld in kubieke waterkasten met respectievelijk 6 of 7 nm zijde (zie aanvullende tabel S4 in [24]); enige 1AKI- of 1UBQ-eiwitten ondergedompeld in kubieke waterboxen met respectievelijk 7,03 of 6,32 nm-zijde (zie aanvullende tabel S10 in [24]); een nanoporie van gehydrateerd silica met een diameter d P =8,13 nm gevuld met 2, 4, 8 of 16 magnetiet nanodeeltjes met een diameter d p =1,97 nm (zie aanvullende tabel S2 in [24]) of 16 magnetietnanodeeltjes met een diameter d p =1,27 nm (zie aanvullende tabel S3 in [24]); en een nanoporie van gehydrateerd silica met een diameter d P =11,04 nm gevuld met 36 of 66 magnetiet nanodeeltjes met een diameter d p =1,27 nm of 20 magnetiet nanodeeltjes met een diameter d p =1,97 nm (zie aanvullende tabel S3 in [24]). Bovendien zijn de nieuwe gesimuleerde opstellingen een nanoporie van gehydrateerd silica met een diameter van d P =8,13 nm gevuld met één 1UBQ-eiwit en een nanoporie van gehydrateerd silica met een diameter van d P =11,04 nm gevuld met 2, 3 of 9 1AKI-eiwitten, of 2, 7, 9 of 12 1UBQ-eiwitten.
Figuur 2 toont het schaalgedrag voor de zelfdiffusiecoëfficiënt van water voor de verschillende eerder genoemde systemen, namelijk bulkwater (D B =2.60×10 −9 m 2 /s), gehydrateerde silica-nanoporiën, gesolvateerde eiwitten en magnetiet-nanodeeltjes, en gehydrateerde silica-nanoporiën gevuld met eiwitten of nanodeeltjes. Zoals verwacht vertoont water in de silica-nanoporiën een verminderde zelfdiffusie, coherent met de toenemende mate van nano-opsluiting die wordt weergegeven door de schaalparameter θ ∗ . Gesuspendeerde moleculen (nanodeeltjes en eiwitten) vertonen een vergelijkbaar effect op de zelfdiffusiecoëfficiënt van water. In Fig. 2 komt de ononderbroken lijn overeen met Vgl. (1) met D C /D B ≈0, wat het limietgeval vertegenwoordigt van de aanname dat nano-opgesloten watermoleculen geen mobiliteit hebben en daarom niet kunnen diffunderen. De stippellijn komt in plaats daarvan overeen met dezelfde vergelijking met een meer realistische waarde van D C =0.39×10 −9 m 2 /s, zoals waargenomen in de simulaties gerapporteerd in [24]:dit model is in staat om de simulatieresultaten nauwkeurig te herstellen (R 2 =0,93), waarmee de goede voorspellingsmogelijkheden van Vgl. (1) ook voor de nieuwe gesimuleerde configuraties.
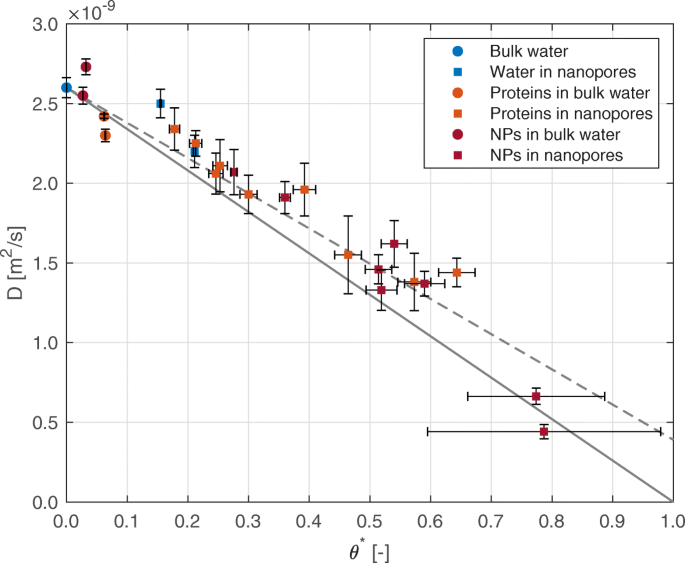
Water zelfdiffusiecoëfficiënt voor verschillende systemen. De zelfdiffusiecoëfficiënt van water wordt weergegeven tegen de schaalparameter θ ∗ voor verschillende systemen. Gegevens voor eiwitten in nanoporiën van silica zijn verkregen via moleculaire dynamica, terwijl de rest van de gegevens uit de aanvullende informatie in [24]. In de legende worden nanodeeltjes afgekort als NP's. De onzekerheden over de waarde van D verwijzen naar de montage van de gemiddelde vierkante verplaatsing (±1 sd); de onzekerheden over de waarde van θ ∗ tot de schatting van het totale volume dat toegankelijk is voor watermoleculen (±1 s.d.). De ononderbroken en onderbroken lijnen rapporteren het model in Vgl. (1) in het geval van D C =0 en D C =0.39×10 −9 m 2 /s, respectievelijk
Voorbeelden van het voorgestelde protocol in de praktijk
Laten we een nanoporeus silicatablet beschouwen dat wordt gebruikt als meetapparaat voor een bekend vervuilend middel in water, zoals voorgesteld. Laten we aannemen dat de tablet lang genoeg wordt ondergedompeld in een oplossingstestmonster zodat de gesuspendeerde vervuilende moleculen in de tablet diffunderen en evenwicht wordt bereikt (zie de volgende sectie voor een gedetailleerde bespreking hiervan). Het monster wordt vervolgens geëxtraheerd en de zelfdiffusiecoëfficiënt van water D binnen de poreuze structuur van de tablet verkregen door bijvoorbeeld QENS-meting. De volumefractie θ ∗ kan dan gemakkelijk worden verkregen uit Vgl. (1), aangezien beide D B en D C bekend zijn bij een bepaalde temperatuur. Vervolgens kan door CPT rekening worden gehouden met de overlappende nanobegrensde volumes water, wat leidt tot θ =− ln(1−θ ∗ ). Voor een enkel type vervuilend middel ingesloten in één nanoporie, Vgl. (2) vereenvoudigt tot
$$\begin{array}{*{20}l} V_{\text{c}} =n_{p} \text{SAS}_{p} \, \bar{\delta}_{p} + \ tekst{SAS}_{P} \, \bar{\delta}_{P} \,, \end{array} $$ (4)zijnde de subscripts p en P verwezen naar respectievelijk de deeltjes en de porie. Zodra het voor oplosmiddel toegankelijke gebied SAS en de gemiddelde karakteristieke lengte van nanoopsluiting \(\bar {\delta }\) voor deeltjes en poriën zijn bekend uit de moleculaire dynamica, het aantal gesuspendeerde deeltjes kan gemakkelijk worden verkregen als
$$\begin{array}{*{20}l} n_{p} =\frac{V_{\text{tot}}\theta-\text{SAS}_{P} \bar{\delta}_{ P}}{\text{SAS}_{p} \bar{\delta}_{p}}. \end{array} $$ (5)De resultaten van deze nanometingsprocedure worden vermeld in Tab. 1 en Fig. 3, voor enkele voorbeeldgevallen van eiwitten en nanodeeltjes in nanoporiën van silica uit Fig. 2. In het bijzonder maakt de bissectrice in Fig. 3 het mogelijk om de nauwkeurigheid van het geschatte aantal gesuspendeerde deeltjes te waarderen \((n_{p }^{e})\) met betrekking tot de originele (werkelijke) ene \((n_{p}^{o})\), zijnde de R 2 van de curve gelijk aan 0,85.
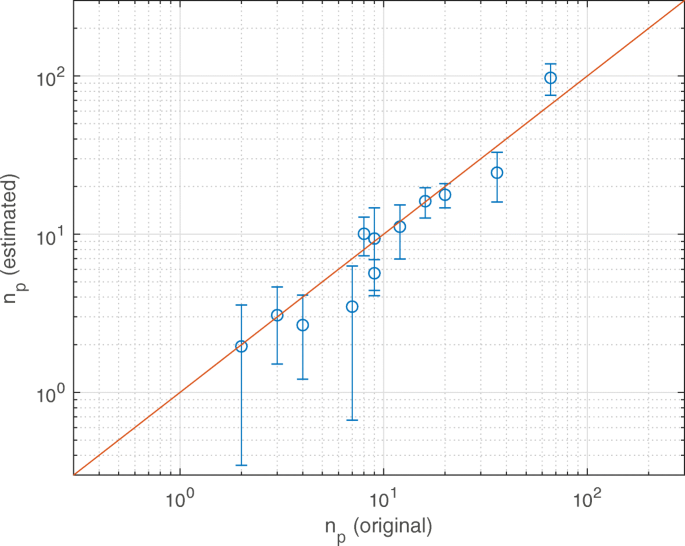
Nauwkeurigheid van het voorgestelde nanometingsprotocol. Geschat aantal deeltjes met behulp van het voorgestelde protocol versus het oorspronkelijke aantal deeltjes. De gerapporteerde gegevens (punten) verwijzen naar de configuraties in Tabel 1; de ononderbroken lijn is de bissectrice. De foutbalken op de waarde van \(n_{p}^{e}\) worden berekend op basis van de variabiliteit van D en V tot waarden (onzekerheidskwantificering, ± 1 s.d.)
Gezien het aantal biomoleculen of nanodeeltjes in de nanoporie, kan hun aantalconcentratie gemakkelijk worden verkregen als c =n p /V P , zijnde \(V_{\text {P}}=T \pi d_{P}^{2}/4\) het vrije volume van de porie in het geval van een cilindrische doorgangsconfiguratie [27] (T is de porielengte, d.w.z. de dikte van de silicatablet in het geval van rechte poriën). Dit nanometerprotocol is hier gepresenteerd voor een enkele porie, maar het zou gemakkelijk kunnen worden geëxtrapoleerd naar de hele nanometertablet gezien de porositeit en dus het aantal gehydrateerde nanoporiën.
Vullen van de nanoporiën
De voorbeelden die in de vorige sectie zijn besproken, houden rekening met evenwichtsomstandigheden, waarbij wordt aangenomen dat de concentratie van deeltjes in de nanoporie gelijk is aan die in de bulkoplossing. Niettemin zou het nanometerprotocol dat in dit werk wordt gesuggereerd, ook het vulproces van nanoporiën door de te detecteren gesolvateerde deeltjes omvatten. In deze sectie beoordelen we de praktische haalbaarheid van het voorgestelde nanometingsprotocol met betrekking tot de karakteristieke vultijd van de nanoporiën.
Het experimentele protocol dat gewoonlijk wordt gebruikt om de vulling van nanoporiën door gesolvateerde nanodeeltjes te maximaliseren, omvat sonicatie- en centrifugatieprocessen [43], wat in sommige gevallen kan leiden tot een niet-uniforme verdeling van deeltjes als gevolg van clustervorming en verstopping van de nanokanalen [44-47 ]. Hier beschouwen we een spontane opzuiging van oplosmiddelen en diffusie van de gedispergeerde deeltjes in de aanvankelijk droge nanoporiën. Daarom hanteren we een vereenvoudigde benadering, rekening houdend met twee opeenvolgende processen vanwege de zeer verschillende tijdschalen van de betrokken verschijnselen:capillaire imbibitie van de droge poriën door de zuivere vloeistof en deeltjesdiffusie door het Fickiaanse mechanisme door de gehydrateerde poriën naar evenwichtsomstandigheden.
Experimenten en moleculair dynamische simulaties [48-50] tonen aan dat als de gemiddelde capillaire diameter groter is dan ongeveer vier keer de moleculaire diameter van water [50, 51], het imbibitieproces kan worden beschreven met de Lucas-Washburn (LW) vergelijking. Bij de benadering van het scherpe front kan de wet van Darcy worden gebruikt om de positie van het bewegende front h te modelleren (t ), waarbij dezelfde vorm van de LW-vergelijking [52] wordt teruggevonden:
$$ h=\sqrt{\frac{2K \Delta p}{\phi_{i} \mu}t}, $$ (6)waar Δ p is de drijvende capillaire druk, μ is de dynamische viscositeit van de vloeistof (in dit geval water), ϕ ik is de effectieve porositeit van het medium aan het begin van het opnameproces, en K is de doorlaatbaarheid ervan. Poreuze silicamaterialen hebben een zeer regelmatige structuur en een smalle poriegrootteverdeling [46]; dus kan hun permeabiliteit worden berekend als [49, 53]:
$$ K=\frac{1}{8}\frac{r_{h}^{4}\phi_{0} }{r_{0}^{2} \tau }, $$ (7)waar r 0 is de nominale poriediameter, r h is de hydraulische diameter van de porie (kleiner dan r 0 vanwege de geadsorbeerde laag watermoleculen op het capillaire oppervlak), ϕ 0 is de nominale porositeit van het medium, en τ is zijn kronkeligheid. De capillaire druk kan worden beschreven met de Young-Laplace-vergelijking:
$$ \Delta p=\frac{2\sigma \cos (\vartheta)}{r_{h}}, $$ (8)waar σ is de oppervlaktespanning van de vloeistof en 𝜗 zijn dynamische contacthoek ten opzichte van het porieoppervlak. Merk op dat, voor silica-water-interfaces, 𝜗 ≈0 [49, 54].
Nanoporeuze tabletten kunnen nauwkeurig worden vervaardigd met rechte cilindrische poriën met een diameter van 5 tot 150 nm en een porositeit van 40 tot 90% [27]. Vergelijking 6 kan worden gebruikt om de tijd te schatten die nodig is voor de volledige imbibitie van een nanoporeus materiaal met dergelijke geometrische kenmerken (t ik ), in de vereenvoudigende hypothese dat verdunde verontreinigingen dit proces niet beïnvloeden. De resulterende t ik worden weergegeven in Fig. 4 met blauwe sterretjes en stippellijn, voor tabletdikte (d.w.z. porielengte) variërend van 1 μ m tot 1 mm. De resultaten laten een opmerkelijke snelheid van het imbibitieproces zien:de dikste macroscopische tablet die wordt beschouwd, is in minder dan 10 s volledig gevuld met water. Om coherente configuraties te analyseren met die gesimuleerd door moleculaire dynamica-opstellingen, zijn de schattingen van t ik overweeg een aanvankelijk droog materiaal (d.w.z. ϕ 0 =ϕ ik ), een gemiddelde poriediameter van d 0 =2r 0 =11,04 nm, porositeit en kronkeligheid gelijk aan ϕ 0 ≈40% en τ ≈1, respectievelijk. Aangezien de hydrodynamische straal rekening moet houden met het effect van geadsorbeerde watermoleculen, r h =r 0 −2d w , waar twee lagen geadsorbeerde watermoleculen (met d w =0,275 nm diameter) worden aangenomen [24]. Het resterende water in de poriën kan redelijkerwijs worden beschouwd onder bulkomstandigheden, en dus, σ =0,072 N/m en μ =10 −3 Pa ·s om T =300 K. Deze schattingen zijn uitgevoerd zonder het effect van de gesuspendeerde deeltjes op het imbibitieproces. De interacties tussen deeltjes en wand zijn echter niet verwaarloosbaar bij hoge volumefracties of voor deeltjes-poriëngrootteverhoudingen die dicht bij de eenheid liggen, omdat lokale eigenschappen van water zoals viscositeit en contacthoek kunnen worden gewijzigd [55]. Toch kan de positie van het vloeistoffront worden beschreven door Vgl. (6) voor deeltjes-poriegrootteverhoudingen van 10% of lager [55].
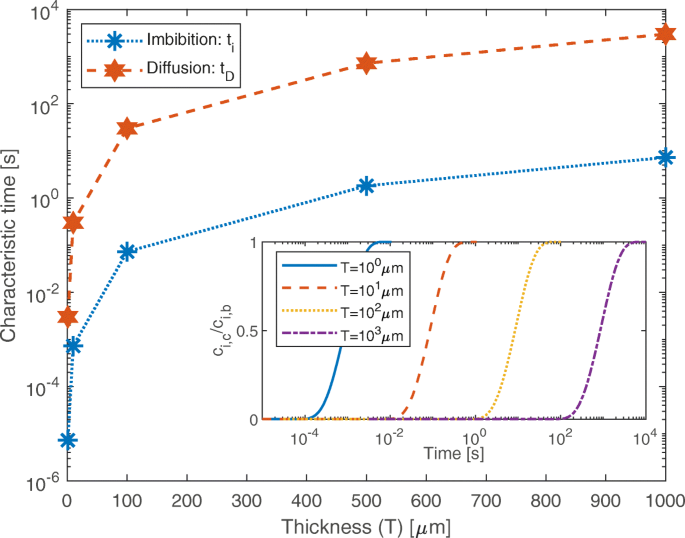
Karakteristieke vultijden van de nanoporiën. Karakteristieke tijden van de nanoporiënvulling door capillariteit (blauwe stippellijn, t ik ) en deeltjesdiffusie (rode stippellijn, t D ) het variëren van de dikte van de nanoporeuze silicatablet (nanoporiën met een diameter van 11,04 nm; oplossing van 1AKI-eiwitten in water met een fractie van 1 gew.%). Het deeltjesdiffusieproces door de volledig gehydrateerde poriën vereist een karakteristieke tijd t D twee ordes van grootte hoger dan t ik , in alle geanalyseerde configuraties. De inzet toont de verhouding tussen de deeltjesconcentratie in het midden van de nanoporie (c ik ,c , bij x =T /2) en de bulk (c ik ,b , bij x =0 en T ) als functie van de tijd voor verschillende diktes (T ) van de tabletten
De karakteristieke tijd die nodig is voor deeltjesdiffusie in de volledig gehydrateerde, homogene en rechte nanoporiën wordt vervolgens beoordeeld. Aangenomen wordt dat dit vulproces berust op pure diffusie [56, 57] en, onder de aanname van verwaarloosbare interacties tussen deeltjes en poriën, kan worden beschreven door de vergelijking van Fick:
$$ \phi_{0}\frac{\partial c_{i}}{\partial t}-D_{e}\nabla^{2} c_{i}=0, $$ (9)c . zijn ik de deeltjesconcentratie, D e =ϕ 0 D p /τ de effectieve diffusie van de deeltjes in de gehydrateerde kanalen, en D p hun diffusiviteit in de bulkvloeistof.
Berekeningen worden uitgevoerd, als een eerste voorbeeld, rekening houdend met een verdunde lysozym (1AKI) oplossing op c ik ,b =3,4 mol/m 3 concentratie, d.w.z. ongeveer 1 gew.% fractie. Vergelijkbaar met de configuratie die wordt gebruikt om t . te schatten ik , silicatabletten met een gemiddelde poriediameter van d 0 =2r 0 =11,04 nm, variërende dikte, porositeit gelijk aan ϕ 0 ≈40% , en kronkeligheid τ ≈1 worden beschouwd. Starting from a fully hydrated pore without any particle inside, the filling time t D is estimated as the time required to reach c ik ,c =0.95c ik ,b at the center of the pore, namely at x =T /2. The particle concentration is constant and equal to c ik ,b at both ends of the channel, namely at x =0 and T . The diffusion coefficient of the lysozyme in water is assumed equal to the bulk value, namely D p =11.08·10 −11 m 2 /s [58, 59]. Equation 9 is solved numerically in one dimension by a finite-element method. The results are reported in Fig. 4 as red stars and dashed line, showing that t D is about two orders of magnitude higher than t ik for a given thickness of the silica tablet. Even in the worst case presented (T =1 mm, t D ≈3000 s), the filling time appears to be compatible with a nano-metering protocol of practical interest. Note that both simulations [60] and experiments [61] in the literature show that the particle diffusivity D p in nanopores can be significantly lower than the bulk one, because of the different affinity of particles with the pore surface and the presence of nanoconfined water with low mobility. Hence, the proposed approach provides initial indications on the characteristic filling time but, to achieve more accurate estimations, D p and thus t D should be analyzed on a case-by-case basis [62].
As a second example, we assess the possibility of metering the concentration of solvated drugs, since they are currently considered as emerging pollutants of water sources [5]. In particular, we analyze one of the relevant drugs for cancer treatment:doxorubicin, which is a hydrophobic molecule commonly used for chemotherapy [63–65]. An estimation of the diffusion time t D of doxorubicin into the hydrated silica nanotablets can be performed under the assumptions already adopted for the previous case study. Unbound doxorubicin has a diffusion coefficient of D p =1.6·10 −10 m 2 /s [66]; thus, a silica tablet with 500 μ m thickness would be filled at 95% of the bulk concentration (c ik ,b =3.4 mol/m 3 ) in approximately 500 s. This illustrative case shows that the proposed nano-metering protocol could be also potentially employed to detect the concentration of drug traces in water. We remark that the effect of additional factors (e.g., chemical affinity between drugs and pore surface, pH, presence of surfactants or functionalizations), which are not considered in this simplified model, should be experimentally investigated, as they may significantly deviate the characteristic time with respect to the considered simplified conditions.
Clearly, the filling time of the nanopores should lie between t ik (best case, nanoparticles are dragged into the pores together with water by capillarity) and t D (worst case, water first hydrates the pores and then nanoparticles follow by Fickian diffusion). Even in the worst explored case, modeling estimations of the filling time of the nanopores indicate a practical feasibility of the proposed nano-metering protocol. This idea is also supported by some promising experimental evidences in the literature. For instance, hydrophilic carbon nanotubes with average diameter of 300 nm are easily filled by spontaneous imbibition with particles in the range of 10–50 nm [67, 68], proving that a proper tuning of the geometrical and chemical parameters of the configuration would provide a fast and homogeneous filling of the nanochannels, thus making the proposed nano-metering protocol feasible.
Implications of the Hypothesis
Inspired by the regular nanoporous structure of diatom algae frustules, in this work, we have presented a new concept for measuring the concentration of nanoparticles or biomolecules dispersed in water. The regular structure of the algae frustules can be artificially reproduced by nanoporous silica tablets, whose pore size, thickness, and shape should be precisely tuned to optimize the selective uptake of particles. The proposed nano-metering method relies on the effect of those nanoparticles or biomolecules on the self-diffusion coefficient of water nanoconfined within the tablet’s pores, and consists in the following steps:
- 1.
Synthesize porous tablet with a controlled size distribution of nanopores.
- 2.
Let the nanopores of the tablet fill with the solution containing the particles to be detected via capillary imbibition and particle diffusion, achieving equilibrium conditions between the nanopores and the surrounding solution.
- 3.
Remove the tablet from the solution and measure the self-diffusion coefficient of water in the hydrated nanopores filled with the particles, e.g., by QENS or D-MRI techniques.
- 4.
Correlate the measured self-diffusion coefficient of water with the particle concentration by means of Eqs. 1 to (5). The solvent accessible surface of nanopore and particles (SAS ) and their mean characteristic length of nanoconfinement (\(\bar {\delta }\)) should be computed from molecular dynamics or taken from available databases.
Molecular dynamic simulations and evidence from the literature have been employed to assess the feasibility of the proposed nano-metering protocol. Hydrated nanopores filled with different concentrations of iron-oxide nanoparticles or proteins have been analyzed, finding agreement between the computed and predicted self-diffusion coefficient of nanoconfined water, thus allowing to estimate the particle concentration. A preliminary analysis of the mechanisms involved in the nanopores filling has been also carried out. Because of the different time scales, two different phenomena have been considered separately:the imbibition of a dry tablet by pure water, driven by capillarity, and the particle diffusion through the hydrated pores, driven by concentration gradient. Results show that the leading characteristic time in the filling process is the time required for particles to diffuse into the hydrated pores; however, the estimated filling time does not exceed 1 h even in case of the thickest tablets considered (1 mm), therefore not compromising the practical feasibility of the nano-metering protocol.
Although the proposed nano-metering method has shown promising results from a numerical point of view, the actual experimental implementation may have to face some additional issues. First, the interaction between the pore surface and particles could be non-negligible and thus alter the filling process (e.g., pores clogging). This effect could generate a bias between the actual concentration of the particles in the bulk solution and the one measured within the pores. Such an issue could be solved by an accurate selection of the surface properties of the pores, which should not interact with the particles to be detected. Second, the current experimental techniques could have difficulty to measure the water diffusivity with a single-nanopore resolution. This issue could be mitigated by measuring the average self-diffusion coefficient over hundreds or thousands of nanopores, which could also provide a better statistical sampling in case of inhomogeneous particle filling throughout the tablet. Third, the uncertainty of the nano-metering protocol should be assessed by experiments. The configurations studied by molecular dynamics have revealed prediction errors up to ± 50% :this error range could be eventually reduced by considering larger statistical samples, both in terms of time (multiple measures) and space (averages over hundreds or thousands of pores). Fourth, the optimal diameter of the nanopores should be determined on the basis of the expected size and concentration of the particles to be detected. On the one hand, the pore size should be chosen to avoid low θ ∗ (e.g., θ ∗ should be> 0.2), since this could lead to negligible variations of the self-diffusivity of water that could be eventually below the resolution of the QENS or D-MRI techniques; on the other hand, high levels of water nanoconfinement should be avoided as well (e.g., θ ∗ should be <0.8), to limit the risk of pore clogging or particle aggregation/segregation and thus biased concentration results.
In conclusion, further research is needed to validate experimentally the original nano-metering protocol discussed in this work. However, the presented numerical results prove the potential of the idea, which may pave the way to a completely new class of detection processes of emerging nanopollutants in water or biomolecules. In perspective, the microscopic size of the metering devices, e.g., nanoporous silica tablets, may allow automation of the nano-metering process through lab-on-a-chip devices.
Beschikbaarheid van gegevens en materialen
De datasets die tijdens het huidige onderzoek zijn gebruikt en/of geanalyseerd, zijn op redelijk verzoek verkrijgbaar bij de corresponderende auteur.
Afkortingen
- 1AKI:
-
Lysozyme
- 1UBQ:
-
Ubiquitin
- CPT:
-
Continuum percolation theory
- D-MRI:
-
Diffusion magnetic resonance imaging
- IONP:
-
Iron oxide nanoparticle
- LINCS:
-
Linear constraint solver
- LW:
-
Lucas-Washburn
- MD:
-
Moleculaire dynamiek
- MOL:
-
Molecule
- MRI:
-
Magnetische resonantie beeldvorming
- NP:
-
Nanodeeltje
- PME:
-
Particle Mesh Ewald
- QENS:
-
Quasi-elastic neutron scattering
- SAS:
-
Solvent accessible surface
Nanomaterialen
- Halfgeleider nanodeeltjes
- Nanocellulose uit blauwgroene algen
- Plasmonische nanodeeltjes
- Over halfgeleidende nanodeeltjes
- Vormingsmechanisme van goed geordende, dicht opeengepakte superroosters van nanodeeltjes afgezet vanuit de gasfase op sjabloonvrije oppervlakken
- Nanotechnologie:van in vivo beeldvormingssysteem tot gecontroleerde medicijnafgifte
- Interactie-effecten bij de assemblage van magnetische nanodeeltjes
- Synthese en luminescentie-eigenschappen van in water oplosbare α-NaGdF4/β-NaYF4:Yb,Er Core–Shell-nanodeeltjes
- Magnetische koolstofmicrosferen als herbruikbaar adsorbens voor het verwijderen van sulfonamide uit water
- 5 voordelen van IoT Smart Water Meters
- Hoe vocht uit perslucht te verwijderen



