Controlebare valleipolarisatie met behulp van dubbele siliceenlijndefecten als gevolg van Rashba Spin-Orbit-koppeling
Abstract
We onderzoeken theoretisch de valleipolarisatie in siliceen met twee parallelle lijndefecten als gevolg van Rashba spin-orbit-koppeling (RSOC). Het is gebleken dat zolang RSOC de intrinsieke spin-orbitkoppeling (SOC) overschrijdt, de transmissiecoëfficiënten van de twee valleien oscilleren met dezelfde periodiciteit en intensiteit, die bestaat uit brede transmissiepieken en nultransmissieplateaus. In de aanwezigheid van een loodrecht elektrisch veld neemt de oscillatieperiodiciteit van de eerste vallei echter toe, terwijl die van de tweede vallei korter wordt, waardoor de overeenkomstige brede piek-nul plateaugebieden worden gegenereerd, waar perfecte polarisatie van de vallei kan worden bereikt. Bovendien kan de polariseerbaarheid van het dal worden gewijzigd van 1 in -1 door de sterkte van het elektrische veld te regelen. Onze bevindingen leggen een andere route vast voor het genereren van in de vallei gepolariseerde stroom met puur elektrische middelen en openen de deur voor interessante toepassingen van halfgeleidervalleitronica.
Inleiding
Siliceen, een laaggebogen monolaag-honingraatrooster van siliciumatomen, is een potentieel aantrekkelijk alternatief voor grafeen voor valleytronic-toepassingen. De structuur met lage knik geeft aanleiding tot relatief grote spin-orbit-koppeling (SOC) in siliceen, en een aanzienlijke energiekloof van ongeveer 1,55 meV wordt geschat op de Dirac-punten K en K ′ [1] Anders dan bij grafeen is de dispersierelatie met lage energie van siliceen eerder parabolisch dan lineair. Gefaciliteerd door de knikstructuur, kan de bandstructuur van siliceen worden gecontroleerd door een elektrisch veld aan te leggen, en zelfs een topologische faseovergang van een quantum spin Hall-isolator naar een quantum Valley Hall-isolator kan optreden [2, 3]. Siliceen is met succes gesynthetiseerd op het oppervlak van substraten zoals Ag(111), Ir(111) en ZrB2(0001)[4-6], en de vrijstaande stabiele structuur ervan is ook voorspeld in verschillende theoretische studies[7] ]. Het belangrijkste is dat een siliceen-veldeffecttransistor (FET) bij kamertemperatuur met succes experimenteel is waargenomen [8]. De afstembaarheid van het elektrische veld en de compatibiliteit met bestaande op silicium gebaseerde apparaten maken siliceen tot een potentieel tweedimensionaal materiaal voor toepassing in de volgende generatie valleytronics.
In tweedimensionale (2D) materialen zoals grafeen en overgangsmetaal dichalcogeniden (MoS2 , enz.), zijn korrelgrenzen tussen twee domeinen van materiaal met verschillende kristallografische oriëntaties ideale keuzes om de valleipolarisatie te bereiken en hebben ze veel aandacht getrokken [9-14]. Onlangs zijn de uitgebreide lijndefecten (ELD's) in siliceen uitgebreid onderzocht volgens eerste-principeberekeningen [15, 16], en de 5-5-8 ELD (hierna afgekort als "lijndefect") bleek de meest stabiele en gemakkelijkst gevormde structuur. De spin- en valleipolarisatie van het siliceenlijndefect is theoretisch onderzocht [17-19]. De vorming van een lijndefect kan worden gevisualiseerd als het naaien van de zigzagranden van twee Si-korrels door de geadsorbeerde Si-atomen, waarbij beide zijden van het lijndefect pseudo-edge-state-achtig gedrag vertonen en de korrelgrenzen van de zigzag-rand fungeren als de pseudo-edge.16 Het is duidelijk dat zo'n rooster spiegelsymmetrie heeft ten opzichte van de lijn defect en de corresponderende roostervectoren in de "linker" en "rechter" domeinen gescheiden door het defect zijn tegengesteld [10, 11]. In zo'n lijndefect met inversiedomeingrens, is de A /B subroosters en vallei-indexen worden uitgewisseld bij het overschrijden van het defect. Het lijndefect is semitransparant voor de quasideeltjes in grafeen en een hoge valleipolarisatie verschijnt met een hoge invalshoek. De polarisatie van de vallei is q j (de groepssnelheid van het elektron langs de y richting) afhankelijk over het lijndefect. Voor grafeen, dat een lineaire dispersie en constante groepssnelheid heeft, kan de polarisatie van de vallei bijna 100% bereiken |q j | (overeenkomend met hoge invalshoek) terwijl het afneemt als |q j | vermindert en verdwijnt als |q j |∼0 [9, 14]. Daarentegen heeft siliceen twee verschillende transmissiekarakteristieken [17, 18]:ten eerste worden de twee valleien niet te onderscheiden omdat de Fermi-energie zich dicht bij de bandrand bevindt vanwege de parabolische dispersierelatie, en ten tweede wordt de transmissie beperkt vanwege de spiraalvormige randtoestand die omgekeerd aan beide zijden van het lijndefect stroomt, zoals weergegeven in figuur 1c. Uiteraard is het systeem met SOC in een bepaalde RSOC een veelbelovende kandidaat voor efficiënte spin-FET. De RSOC genereert een effectief magnetisch veld in het vlak en induceert de spin-precessie die loodrecht op het opsluitingsvlak wordt geïnjecteerd. De spinpolarisatie [20] en inversie [21] zijn onderzocht in gated siliceen nanoribbons. Theoretische berekeningen hebben aangetoond dat de energieband van siliceen significant kan worden gemoduleerd door RSOC [22, 23]. Bijvoorbeeld, bij een relatief sterke RSOC, de spin-down (-up) band bij de K (K ′ ) vallei verschuift terwijl de andere spinbanden in de geleidingsband ongewijzigd blijven. Gezien het bijzondere transmissiekenmerk in het siliceenlijndefect en het effect van RSOC in siliceen, worden de praktische volledig elektrische schema's voor het genereren van in het dal gepolariseerde dragers haalbaar.
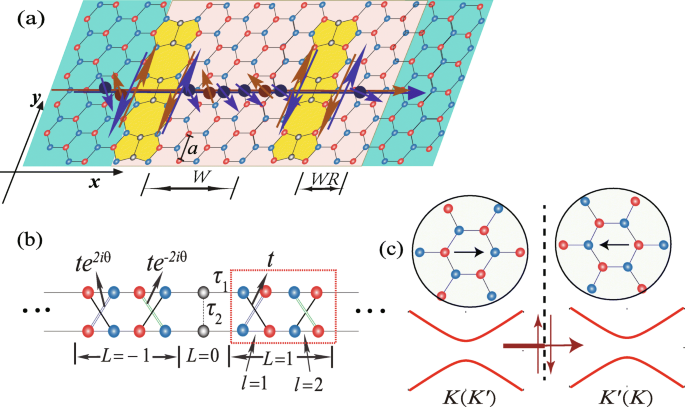
een Schematisch diagram van het precessieproces van de toestanden (K ,↑ )(rode bol) en (K ′ ,↓ )(blauwe bol) door een siliceenvel met twee parallelle lijndefecten, waarbij de blauwe (rode) cirkel de A aangeeft (B ) subrooster. De toestanden (K ,↑ ) en (K ′ ,↓ ) circuleren langs de pseudo-rand, en het RSOC en het elektrische veld worden verondersteld aanwezig te zijn in het Franse grijze gebied. W (W =2) en WR (WR =1) geeft de breedte van het verstrooiingsgebied weer in eenheden van \(\sqrt {3}a\). b Het vereenvoudigde roostermodel van het oneindige siliceen met een lijndefect, waarbij θ =k j een en de gestippelde rechthoek komt overeen met een supercel. In de eenheidscel worden de roosterpunten gespecificeerd door een reeks indices (L,l ). c De transmissie voor één spin-status in de K (K ′ ) dal over lijndefect met inversiedomeingrenzen. De inzetstukken tonen de oriëntatie van het kristalrooster in de twee domeinen gescheiden door het lijndefect (stippellijn). De dikke/dunne lijnen geven aan dat de transmissie over het lijndefect wordt tegengehouden door de spiraalvormige randtoestanden die omgekeerd langs de pseudorand vloeien
In dit artikel stellen we een efficiënte manier voor om de Dirac-fermionen van verschillende valleien te polariseren met behulp van de siliceen dubbele lijndefecten, waardoor een duidelijke valleipolarisatie wordt gecreëerd door gebruik te maken van het elektrische veld in siliceen. Onze resultaten laten zien dat wanneer de Fermi-energie zich in de buurt van de onderkant van de geleidingsband bevindt, de oscillatiebeelden van de transmissiecoëfficiënten van twee valleien, die brede oscillerende pieken en dieptepunten omvatten, samenvallen zolang RSOC de intrinsieke SOC overschrijdt, terwijl de aanwezigheid van slechts een enkel lijndefect kan de vallei-afhankelijke elektronen niet verspreiden. Wanneer er twee parallelle lijndefecten zijn, evolueren de oscillerende dieptepunten naar nultransmissieplateaus, en effectieve modulatie van dalafhankelijk transport kan worden gerealiseerd door de oscillatieperiodiciteit van de twee Dirac-valleien te veranderen met een loodrecht elektrisch veld, waarbij de oscillatieperiodiciteit van de twee valleien nemen toe en af en leiden tot de perfecte valleipolarisatie bij de corresponderende regio's van het brede piek-nulplateau. In een experiment kan men zo'n zuivere dalstroom detecteren door de verandering van geleiding met het elektrische veld te meten. Dit fenomeen biedt een andere route voor het effectief moduleren van de valleipolarisatie in siliceenapparaten door gebruik te maken van de RSOC en elektrische velden.
Methoden
Laten we uitgaan van het schema van een twee-terminal siliceenlijndefectapparaat, zoals getoond in Fig. 1a, waarin de spin-precessie wordt geïllustreerd om de vallei-gepolariseerde stroom te genereren als gevolg van het RSOC en het elektrische veld. Er wordt verondersteld dat RSOC bestaat aan één kant van het lijndefect met breedte W en WR in eenheden van \(\sqrt {3}a\), waarbij a =3,86 Å is de roosterconstante van ongerept siliceen, zoals weergegeven in figuur 1a. Wanneer de Fermi-energie zich aan de onderkant van de geleidingsband bevindt, zijn de toestanden (K ,↓ )[ (K ,↓ ) komt overeen met een staat in de vallei K met ↓ (omlaag) draaien] en (K ′ ,↑ ) zitten in het gat vanwege de manipulatie van de energieband van RSOC. De andere twee staten, (K ,↑ ) en (K ′ ,↓ ), circuleren langs de pseudo-rand vanwege de spin-momentum-vergrendelingskarakteristiek van SOC [24], zoals weergegeven in figuur 1a. Voor een definitieve spin-toestand stroomt het langs de pseudo-rand met tegengestelde richtingen aan beide zijden van het lijndefect dat als een filter kan werken en de transmissie over het lijndefect kan beperken, zoals weergegeven in Fig. 1c.
Een roostermodel in de strak bindende weergave wordt gebruikt om het lijndefectsysteem met RSOC te beschrijven als [17, 22]
$$\begin{array}{@{}rcl@{}} H&=&t\sum_{\langle i,j\rangle\alpha}c_{i\alpha}^{\dag}c_{j\alpha}+ \tau_{2}\sum_{\langle \gamma\delta\rangle\alpha}c_{i_{y}\alpha,\gamma}^{\dag}c_{i_{y}\alpha,\delta}+ \ tau_{1}\sum_{\langle i,\gamma\rangle\alpha}c_{i\alpha}^{\dag}c_{i_{y}\alpha,\gamma}\\ &+&i\frac{t_ {so}}{3\sqrt{3}}\sum_{\langle\langle i,j\rangle\rangle\alpha\beta}\nu_{ij}c^{\dag}_{i\alpha}\sigma_ {\alpha\beta}^{z}c_{j\beta}+\Delta_{z}\sum_{i\alpha}\mu_{i} c_{i\alpha}^{\dag}c_{i\alpha }\\ &+&it_{R}\sum_{\langle i,j\rangle\alpha\beta}c_{i\alpha}^{\dag}(\vec{\sigma}\times\mathrm{\mathbf{ d_{ij}}})^{z}_{\alpha\beta}c_{j\beta}+Hc, \end{array} $$ (1)waarbij \(c_{i\alpha }^{\dag }\) en \(c_{i_{y}\alpha,\gamma /\delta }^{\dag }\) de elektronencreatie-operator vertegenwoordigen met spin α op siliceensite i en het lijndefect, respectievelijk, en 〈〉/〈〈〉〉 loopt over alle dichtstbijzijnde-/volgende-dichtstbijzijnde-buur-hopping-sites. De eerste drie termen duiden het hoppen van de naaste buren aan en de parameters t ,τ 1 , en τ 2 duiden verschillende springenergieën van de naaste buren aan in het nauwsluitende model, zoals weergegeven in figuur 1b. De vierde term is de effectieve SOC met de hopping-parameter t dus , en ν ij =±1 voor linksom (met de klok mee) hoppen tussen de volgende dichtstbijzijnde aangrenzende locaties ten opzichte van de positieve z -as. Een theoretisch onderzoek [16] heeft aangetoond dat de twee dichtstbijzijnde Si-atomen in het defecte gebied relatief identiek zijn aan die in het ongerepte gebied en dat alle Si-atomen in de sp blijven. 2 −sp 3 gehybridiseerde staat. Daarom is het redelijk om τ . in te stellen 2 =τ 1 =t . In de vijfde termijn, Δ z is de verspringende subroosterpotentiaal die ontstaat uit een elektrisch veld loodrecht op de siliceenplaat, en μ ik =±1 voor de A (B ) website. De laatste term vertegenwoordigt de extrinsieke RSOC-term waarbij t R is de Rashba spin-orbit hopping parameter. d ij is de eenheidsvector die wijst vanaf site j naar ik , en \(\vec {\sigma }=(\sigma ^{x},\sigma ^{y},\sigma ^{z})\) in Vgl. 1 is de vector van echte spin Pauli-matrices. De RSOC komt voort uit een extern potentieel dat wordt aangelegd door een elektrische poort, metaalatoomadsorptie of een substraat [20, 25] dat de structuurinversiesymmetrie van siliceen dramatisch kan doorbreken. Met name de extrinsieke RSOC die afkomstig is van het elektrische veld wordt genegeerd omdat het erg zwak is.
De ELD's van siliceen worden getoond in Fig. 1a, die zich enorm uitstrekt langs de y richting. De translatiesymmetrie van de roosterstructuur langs de y richting geeft aan dat k j een behouden grootheid is en dat de creatie (annihilatie)-operatoren als volgt kunnen worden herschreven, volgens de Fourier-transformatie (de spin-index wordt genegeerd)[17]:
$$\begin{array}{@{}rcl@{}} c_{i}^{\dag}=\sum_{k_{y}}c_{k_{y},i_{x}}e^{- 2ik_{y}i_{y}a},c_{i}=\sum_{k_{y}}c_{k_{y},i_{x}}e^{2ik_{y}i_{y}a}, \\ c_{i_{y},\gamma}^{\dag}=\sum_{k_{y},\gamma}c^{\dag}_{k_{y},\gamma}e^{-2ik_ {y}i_{y}a},c_{i_{y},\gamma}=\sum_{k_{y},\gamma}c_{k_{y},\gamma}e^{2ik_{y}i_ {j}a}. \end{array} $$ (2)Dan is de Hamiltonmatrix in Vgl. 1 is ontkoppeld in \(H=\sum _{k_{y}}H_{k_{y}}\), waarbij \(H_{k_{y}}\) kan worden beschreven in de volgende vorm:
$$ {\begin{aligned} H_{k_{y}}=-\sum_{i}\varphi_{i,1}^{\dag}\hat{T}_{11}\varphi_{i,1} -\sum_{i}\varphi_{i,2}^{\dag}\hat{T}_{22}\varphi_{i,2}\\ -\sum_{i}\varphi_{i,1}^ {\dag}\hat{T}_{12}\varphi_{i,2}-\sum_{i\neq-1}\varphi_{i,2}^{\dag}\hat{T}_{23 }\varphi_{i+\hat{x},1}\\ -\varphi_{\bar{1},2}^{\dag}\hat{T}_{\bar{1}0}\varphi_{0 }-\varphi_{0}^{\dag}\hat{T}_{01}\varphi_{1,1}-\varphi_{0}^{\dag}\hat{T}_{00}\varphi_ {0} -\varphi_{\bar{1},2}^{\dag}\hat{T}_{\bar{1}1}\varphi_{1,1}+hc, \end{aligned}} $$ (3)waar \(\varphi _{i,l}^{\dag }=\left [ c_{{{k}_{y}},i,l,A\uparrow }^{\dag }, c_{{{ k}_{y}},i,l,A\downarrow }^{\dag }, c_{{{k}_{y}},i,l,B\uparrow }^{\dag },c_{ {{k}_{y}},i,l,B\downarrow }^{\dag }\right ]\), i in de set van index (i,l ) staat voor de positie van een supercel \((\bar {i}=-i)\), en l =1 of 2 geeft verschillende zigzagketens in een supercel aan, zoals weergegeven in de gestreepte rechthoek in figuur 1b. \(\hat {T_{ll'}}\) vertegenwoordigt de Hamiltoniaanse matrix van elke zigzagketen (l =l ′ ) in een supercel of het samenspel tussen verschillende zigzagketens (l ≠l ′ ).
Opgemerkt wordt dat de twee valleien K en K ′ zijn nu gegoten op [0,±π /3een ] vanwege het invoegen van het lijndefect. De transmissiematrix van de η (η =K /K ′ ) dal wordt berekend met behulp van de algemene Landauer-formule[26, 27],
$$\begin{array}{@{}rcl@{}} T={\left(\begin{array}{cc} T^{\uparrow\uparrow}_{\eta} &T^{\uparrow\ downarrow}_{\eta} \\ T^{\downarrow\uparrow}_{\eta} &T^{\downarrow\downarrow}_{\eta} \end{array} \right)}=\sum_{i ,j=1}^{8}{ \left(\begin{array}{cc} \vert t_{ij,\eta}^{\uparrow\uparrow}\vert^{2} &\vert t_{ij, \eta}^{\uparrow\downarrow}\vert^{2} \\ \vert t_{ij,\eta}^{\downarrow\uparrow}\vert^{2} &\vert t_{ij,\eta} ^{\downarrow\downarrow}\vert^{2} \end{array} \right)}, \end{array} $$ (4)waar
$$\begin{array}{@{}rcl@{}} t=2\sqrt{-Im\Sigma_{L}}G^{r}\sqrt{-Im\Sigma_{R}} \end{array } $$ (5)en
$$\begin{array}{@{}rcl@{}} t_{ij,\eta}^{\uparrow\uparrow}&=t_{2(i-1)+1,2(j-1)+ 1}\\ t_{ij,\eta}^{\uparrow\downarrow}&=t_{2(i-1)+1,2j}\\ t_{ij,\eta}^{\downarrow\uparrow}&=t_{2i,2(j-1)+1}\\ t_{ij,\eta}^{\downarrow\downarrow}&=t_{2i,2j}. \end{array} $$ (6)Hier, \(-Im\Sigma _{L,R}=-\links (\Sigma _{L,R}^{r}-\Sigma _{L,R}^{a}\right)/ 2i\ ) zijn positieve semidefinite matrices met een goed gedefinieerde matrixwortel, waarbij \(\Sigma _{L,R}^{a}=\left [\Sigma _{L,R}^{r}\right ]^{ \dag }\) zijn de vertraagde/geavanceerde zelfenergie van de linker/rechter afleiding. De 16×16 submatrix G r is de functie van de vertraagde Groen, die de eerste en laatste supercel verbindt langs de x richting en kan worden berekend met behulp van de recursieve functiemethode van Green. De totale transmissiecoëfficiënten van de η vallei zijn \(T_{\eta }=T^{\uparrow \uparrow }_{\eta }+T^{\uparrow \downarrow }_{\eta }+ T^{\downarrow \uparrow }_{\eta }+T^{\downarrow \downarrow }_{\eta }\), en de spinpolarisatie P s en vallei polarisatie P η kan worden gegeven door
$${\begin{aligned} P_{s}&=\frac{T_{K}^{\uparrow\uparrow}+T_{K}^{\uparrow\downarrow}-T_{K}^{\downarrow\ downarrow}-T_{K}^{\downarrow\uparrow}+T_{K'}^{\uparrow\uparrow}+T_{K'}^{\uparrow\downarrow}-T_{K'}^{\downarrow \downarrow}-T_{K'}^{\downarrow\uparrow}}{T_{K}+T_{K^{\prime}}},\\ P_{\eta}&=\frac{T_{K} -T_{K^{\prime}}}{T_{K}+T_{K^{\prime}}}. \end{aligned}} $$Resultaten en discussie
In de berekeningen van de spinafhankelijke transmissiecoëfficiënten stellen we τ 2 =τ 1 =t =1 als de energie-eenheid, de SOC-sterkte t dus =0.005t , en de Fermi-energie E f =1.001t dus , die zich aan de onderkant van de geleidingsband bevindt. De breedte van het verstrooiingsgebied is W =1000 voor het enkele lijndefect en een extra breedte WR=1000 wordt ook in aanmerking genomen voor de twee parallelle lijndefecten, zoals weergegeven in Fig. 1a.
Figuur 2 toont de spin-geconserveerde/spin-flip transmissiecoëfficiënten van vallei \(\eta, T^{sc}_{\eta }/T^{sf}_{\eta }\), als functie van het incident hoeken α (a) en van de RSOC-sterkte t R (b–d). Figuur 2a-c komt overeen met het geval van het enkele lijndefect, en (d) is voor het geval van de twee parallelle lijndefecten. Het is aangetoond dat bij een bepaalde t R (bijvoorbeeld t R =5t dus zoals in Fig. 2a), zijn de spinafhankelijke transmissiecoëfficiënten \(T^{sc}_{K}/T^{sf}_{K}\) constant en onafhankelijk van de invalshoeken vanwege de parabolische dispersierelatie , zoals getoond in Fig. 2a. Daarom kunnen we in de volgende berekeningen de invalshoek α . gebruiken =0 als voorbeeld. Voor een zwakke t R , verschijnt een oscillerend fenomeen vergelijkbaar met dat in een tweedimensionaal elektronengas [26, 27] als gevolg van de Rashba-splitsing, zoals weergegeven in de inzet van figuur 2b. Als t R neemt toe (t R >t dus ), \(T_{K}^{\uparrow \uparrow }\) en \(T_{K}^{\uparrow \downarrow }\) hebben dezelfde oscillerende periodiciteit en bijna dezelfde grootheden als t R die bestaat uit enkele oscillatiepieken en nadirs, terwijl \(T_{K}^{\downarrow \downarrow }/T_{K}^{\downarrow \uparrow }\) naar nul neigt omdat de Fermi-energie in zijn opening ligt, zoals getoond in Fig. 2b. Dus de totale transmissiecoëfficiënt van K vallei wordt voornamelijk bijgedragen door de spin-up staat. In feite zijn de oscillatiebeelden van de twee valleien, K en K ′ , samenvallen terwijl de transmissiecoëfficiënten van K ′ vallei wordt voornamelijk bijgedragen door de spin-down elektronen.
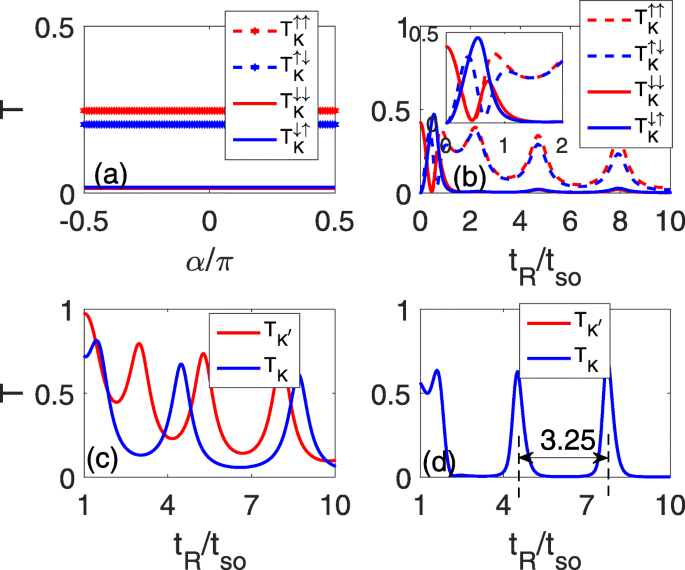
Spin-geconserveerde en spin-flip transmissiecoëfficiënten als functies van de invalshoeken α bij t R =5t dus in een en als functies van de RSOC-sterkte t R in b –d , waar een -c zijn voor het enkele regeldefect en d is voor de twee parallelle lijndefecten, met Δ z =0.2t dus in c
In de aanwezigheid van een loodrecht elektrisch veld wordt de degeneratie van de vallei opgeheven en verschilt het oscillerende gedrag van de twee valleien:de oscillerende periodiciteit van de K vallei neemt toe, terwijl die van de K ′ vallei neemt af, zoals weergegeven in Fig. 2c. Het lijkt echter onhaalbaar om één conische valleitoestand te filteren met slechts één lijndefect, omdat de oscillerende dieptepunten een bepaalde grootte hebben. Natuurlijk kan men het oscillerende fenomeen met twee parallelle lijndefecten beschouwen om de transmissie verder te beperken, zoals weergegeven in figuur 2d. Vergelijking van Fig. 2b met d onthult dat de oscillatiepiek smal en acuut wordt, terwijl het oscillatienadir breder en zwakker wordt, wat het nultransmissieplatform vormt. De ruimte tussen twee aangrenzende oscillatiepieken is vastgesteld op 3,25t dus , zoals gekenmerkt door de twee stippellijnen in Fig. 2d.
Om een beter dalfiltereffect te bereiken, concentreren we onze aandacht op het effect van het loodrechte elektrische veld. De resultaten van dit effect worden getoond in figuur 3. Zoals hierboven besproken, verandert de oscillerende periodiciteit van de twee valleien op een tegengestelde manier, en worden de oorspronkelijke overlappende oscillatiepieken in figuur 2d verlicht. Ondertussen wordt het nultransmissieplateau breder en smaller voor T K en \(T_{K^{\prime }}\), respectievelijk, zoals weergegeven in Fig. 3a en b. Bij Δ z =0.15t dus , ontwikkelt de ruimte tussen de twee aangrenzende oscillatiepieken zich tot 3.6t dus voor T K , terwijl het is teruggebracht tot 3.1t dus voor \(T_{K^{\prime }}\), zoals aangegeven door de twee blauwe en rode stippellijnen in Fig. 3a. Naarmate het elektrische veld sterker wordt, blijft de ruimte tussen de twee aangrenzende oscillatiepieken toenemen/afnemen gedurende T K /\(T_{K^{\prime }}\), wat 5,4t is dus /2.8t dus bij Δ z =0.3t dus , zoals getoond in Fig. 3b. De verandering in de oscillatieperiodiciteit zal leiden tot de overeenkomstige regio's van een breed piek-nulplateau, waar perfecte valleipolarisatie met P η =±1 plateaus kunnen worden gerealiseerd, zoals weergegeven in Fig. 3c en d. Tegelijkertijd wordt aangetoond dat hoge spinpolarisatie P s treedt ook op wanneer P η =±1.
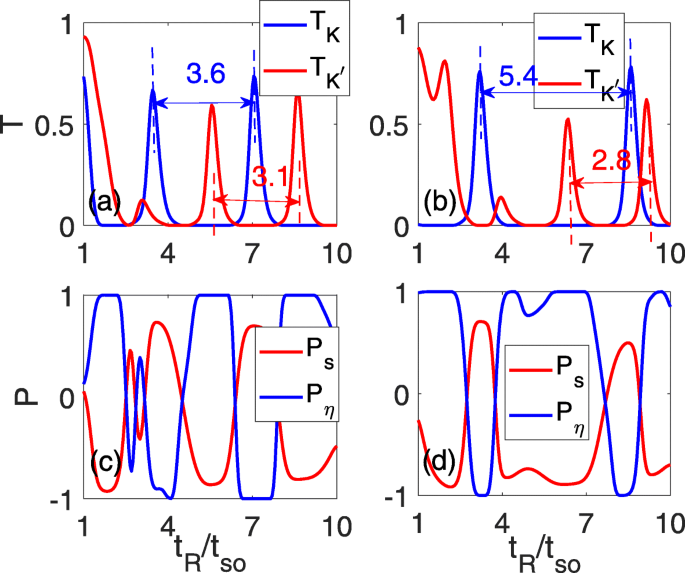
De totale transmissiecoëfficiënten \(T_{K}/T_{K^{\prime }}\) (a , b ) en de spin/vallei-polarisatie (c , d ) als functie van de RSOC-sterkte t R voor verschillende subroosterpotentialen. Δ z =0.15t dus in een en c en Δ z =0.3t dus in b en d; de andere parameters zijn identiek aan die in Fig. 2d
Vanwege de onbeheersbaarheid van RSOC is het echter nog steeds moeilijk om dergelijke zuivere dalstromen experimenteel te detecteren, hoewel de RSOC die wordt geïnduceerd in het lijndefect groter kan zijn dan de intrinsieke SOC. Om de pure valleistroom gemakkelijk experimenteel te onderzoeken, onderzoeken we ook de transmissiecoëfficiënten en de polarisatie van de vallei als een functie van het elektrische veld, dat tijdens een experiment continu kan worden gecontroleerd. Er wordt aangetoond dat de perfecte valleipolarisatie met P η =±1 kan voorkomen in een bepaald bereik van Δ z en dat het kan veranderen van P η =1 tot P η =1 naarmate het elektrische veld toeneemt, zoals weergegeven in figuur 4a. Voor een definitieve t R (bijvoorbeeld t R =7.2t dus , zoals aangegeven met een stippellijn in Fig. 4a), oscilleren de transmissiecoëfficiënten \(T_{K}/T_{K^{\prime }}\) met Δ z , waar de brede transmissiepieken van de K (K ′ ) vallei komen overeen met de nultransmissieplateaus van de K ′ (K ) vallei. De totale transmissiecoëfficiënten worden in principe bijgedragen door één vallei, aangezien het elektrische veld varieert, en perfecte polarisatie van de vallei kan altijd optreden rond de maximale waarde van \(T_{K}/T_{K^{\prime }}\), zoals weergegeven in Afb. 4b. Terwijl de Fermi-energie vanaf de rand van de band vertrekt, kan de perfecte polarisatie van de vallei nog steeds overleven, zelfs bij E f =1.5t dus , waar de plateaurelatie goed kan worden gehandhaafd, zoals weergegeven in figuur 4c. Tijdens een experiment kan men de vallei-gepolariseerde elektrische stromen van links naar rechts analyseren met een experimenteel meetbare grootheid zoals de conductantie, die evenredig is met de totale transmissiecoëfficiënt. De maximale geleiding tussen twee minimumwaarden (soms zijn ze nul) moet van één dal zijn. We kunnen de grootte van de geleidbaarheid schatten volgens de formule \(G=\frac {e^{2}}{h}\int _{-k_{F}}^{k_{F}}T\frac {dk_ {y}}{2\pi /L_{y}}=\frac {e^{2}}{h}\frac {Ly\sqrt {E^{2}-t^{2}_{so}} }{2\pi \hbar v_{F}}2T\) [28], waarbij L j =2een ≈7.72Å is de breedte van het siliceenlijndefect, v F =5,5×10 5 m /s is de Fermi-snelheid, \(\hbar =h/2\pi \) is de gereduceerde constante van Planck met \(\phantom {\dot {i}\!}h=4.13566743\times 10^{-15}eV\cdot s, T=T_{K}+T_{K'}\) is de totale transmissiecoëfficiënt en E is de on-site energie van de invallende elektronen. Dan is de geleiding ongeveer \(G\circa \left [0.7T\sqrt {E^{2}-t^{2}_{so}}/eV\right ]\frac {e^{2}}{ H}\). Het blijkt ook dat naarmate de energie ter plaatse aan de incidentzijde wordt verhoogd tot E =0.15t (t =1.6eV ), veranderen de transmissiecoëfficiënten van de twee valleien slechts een klein beetje in vergelijking met figuur 4c als gevolg van behoud van spin en momentum en blijft de transmissiepiek-nulplateau-relatie nog steeds behouden, zoals weergegeven in figuur 4d. In dit geval is de geleiding ongeveer \(G\ongeveer 0,17T\frac {e^{2}}{h}\), wat aanzienlijk is en in het experiment detecteerbaar is. Het energievenster om dit fenomeen waar te nemen is ongeveer 0,5t dus (t dus <E <1.5t dus ) wat evenredig is met t dus . In experiment is het niet moeilijk om de Fermi-energie nabij de bandrand te regelen en de SOC-gap kan zelfs radicaal worden vergroot tot 44 meV door de nabijheid van Bi (111) dubbellaag [29] die het energiegebied aanzienlijk kan verbeteren om de pure te detecteren. dal stroom. Bovendien kan het rekenmodel ook worden toegepast op andere tegenhangers met een lage knik van grafeen, germaneen[30], staneen en MoS2 [31–36], die nog grotere bandafstanden hebben [37, 38] evenals de SOC-sterkten (SOC-sterkte kan 0,1 eV bereiken voor staneen [38, 39]). In een echt experiment is het gemakkelijk om een sterke RSOC te realiseren die de intrinsieke SOC kan overschrijden door de spiegelsymmetrie in het vlak met het speciale substraat te doorbreken [40]. Daarom kan dit schema experimenteel volledig uitvoerbaar zijn.
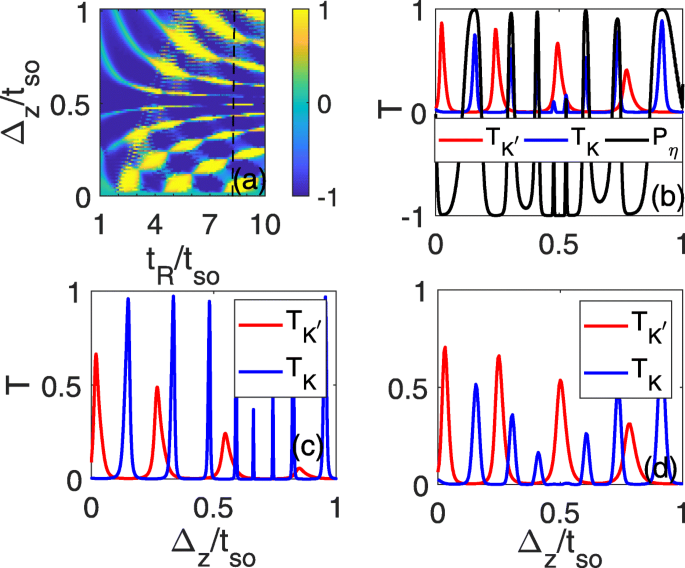
Vallei polarisatie a en \(T_{K}/T_{K^{\prime }}\) (b –d ) als functies van Δ z en t R . t R =7.2t dus in (b –d ), E f =1.5t dus in c en d , en de energie ter plaatse is E =0.15t in de linker elektrode in d; alle andere parameters zijn identiek aan die in Fig. 2d
Conclusies
We hebben een elektrische methode voorgesteld voor het genereren van een dal-gepolariseerde stroom in siliceenlijndefecten. In schril contrast met de conventionele elektrische benaderingen die worden gebruikt om dal-gepolariseerde stroom te produceren, onderzoeken we de RSOC, waarvan wordt aangenomen dat deze de veelgebruikte spinpolarisatie in spin-gepolariseerde FET's afstemt. Het blijkt dat de transmissiecoëfficiënten van de twee valleien oscilleren met dezelfde periodiciteit en intensiteit, die is samengesteld uit transmissiepieken en nultransmissieplateaus. De dal-gepolariseerde stroom kan worden gegenereerd door de oscillerende periodiciteit van de twee valleien af te stemmen met een elektrisch veld, dat de symmetrie van de dalstaten kan vernietigen en de corresponderende transmissiepiek-nul plateaugebieden kan bewerkstelligen. Bovendien bieden we ook een schema om de pure valleistroom in experiment te detecteren en de resultaten kunnen licht werpen op de manipulatie van in de vallei gepolariseerde stromen met elektrische middelen.
Beschikbaarheid van gegevens en materialen
De datasets die zijn gegenereerd tijdens en/of geanalyseerd tijdens het huidige onderzoek zijn op redelijk verzoek verkrijgbaar bij de corresponderende auteurs.
Afkortingen
- 2D:
-
Tweedimensionaal
- ELD:
-
Uitgebreid lijndefect
- FET:
-
Veldeffecttransistor
- RSOC:
-
Rashba spin-baan koppeling
- SOC:
-
Intrinsieke spin-baankoppeling
Nanomaterialen
- Contactloze vloeistofniveaumeting met een reflectometerchip
- Hoe RAM vanuit een bestand te initialiseren met TEXTIO
- Op weg naar 7nm
- Hoeken gebruiken om de toekomst van elektronica te verbeteren
- Slim beton met nanodeeltjes
- C#-gegevenstypen met voorbeeld:Learn Int | drijven | Dubbel | Char
- Facebook Login met Python:FB Login Voorbeeld
- High-throughput fabricage van hoogwaardige nanovezels met behulp van een gemodificeerd vrij oppervlak elektrospinning
- Gietdefecten:soorten, oorzaken en oplossingen
- Voorkomen van lasproblemen en defecten door het gebruik van geverifieerde metalen
- 5 goedkope manieren om industriële automatisering 4.0 te gaan gebruiken voor lijnverbeteringen



