Binaire toevoeging

De regels voor binaire toevoeging

Het toevoegen van binaire getallen is een zeer eenvoudige taak en lijkt erg op het met de hand optellen van decimale getallen. Net als bij decimale getallen, begin je met het toevoegen van de bits (cijfers) één kolom, of plaats je het gewicht, van rechts naar links, per keer.

In tegenstelling tot decimaal optellen, is er weinig te onthouden op het gebied van regels voor het optellen van binaire bits:

0 + 0 =0 1 + 0 =1 0 + 1 =1 1 + 1 =10 1 + 1 + 1 =11 

Net als bij decimale optelling, wanneer de som in één kolom een ​​getal van twee bits (twee cijfers) is, wordt het minst significante cijfer geschreven als onderdeel van de totale som en wordt het meest significante cijfer "gedragen" naar de volgende linkerkolom . Bekijk de volgende voorbeelden:

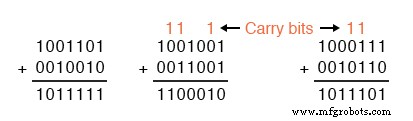
Het optellingsprobleem aan de linkerkant vereiste dat er geen bits gedragen moesten worden, aangezien de som van de bits in elke kolom ofwel 1 of 0 was, niet 10 of 11. Bij de andere twee problemen waren er zeker bits die gedragen moesten worden, maar het proces toevoegen is nog steeds vrij eenvoudig.

Binaire toevoeging is de basis van digitale computers

Zoals we later zullen zien, zijn er manieren waarop elektronische circuits kunnen worden gebouwd om deze taak van optellen uit te voeren, door elk bit van elk binair getal weer te geven als een spanningssignaal (ofwel "hoog", voor een 1; of "laag" voor een 0). Dit is de basis van alle rekenkunde die moderne digitale computers uitvoeren.

GERELATEERDE WERKBLAD:

• Werkblad binaire wiskunde