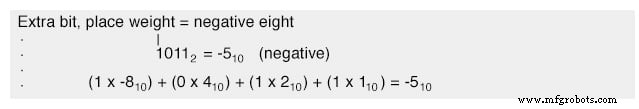Negatieve binaire getallen

Omdat optellen gemakkelijk kan worden bereikt, kunnen we de bewerking van aftrekken met dezelfde techniek uitvoeren door simpelweg een van de getallen negatief te maken. Het aftrekprobleem van 7 - 5 is bijvoorbeeld in wezen hetzelfde als het optelprobleem 7 + (-5).

Omdat we al weten hoe we positieve getallen binair moeten weergeven, hoeven we nu alleen nog maar te weten hoe we hun negatieve tegenhangers moeten weergeven en kunnen we ze aftrekken.

Gewoonlijk stellen we een negatief decimaal getal voor door een minteken direct links van het meest significante cijfer te plaatsen, net als in het bovenstaande voorbeeld, met -5. Het hele doel van het gebruik van binaire notatie is echter om aan/uit-circuits te construeren die bitwaarden kunnen vertegenwoordigen in termen van spanning (2 alternatieve waarden:"hoog" of "laag").

In deze context hebben we niet de luxe van een derde symbool zoals een "min"-teken, aangezien deze circuits alleen aan of uit kunnen zijn (twee mogelijke toestanden). Een oplossing is om een ​​bit (circuit) te reserveren dat niets anders doet dan het wiskundige teken voorstellen:

Zoals je kunt zien, moeten we voorzichtig zijn als we bits gaan gebruiken voor een ander doel dan de standaard plaatsgewogen waarden. Anders 1101₂ kan verkeerd worden geïnterpreteerd als het getal dertien, terwijl we in feite negatief vijf bedoelen.

Om de zaken hier recht te houden, moeten we eerst beslissen hoeveel bits er nodig zijn om de grootste getallen weer te geven waarmee we te maken hebben, en dan ervoor zorgen dat we die bitveldlengte niet overschrijden in onze rekenkundige bewerkingen.

Voor het bovenstaande voorbeeld heb ik me beperkt tot de weergave van getallen vanaf min zeven (1111₂ ) tot positief zeven (0111₂ ), en niet meer, door van het vierde bit het "teken" -bit te maken. Alleen door eerst deze limieten vast te stellen, kan ik verwarring van een negatief getal met een groter, positief getal voorkomen.

Negatief vijf weergeven als 1101₂ is een voorbeeld van het teken-magnitude systeem van negatieve binaire nummering. Door het meest linkse bit als tekenindicator te gebruiken en niet als plaatsgewogen waarde, offer ik de "pure" vorm van binaire notatie op voor iets dat me een praktisch voordeel geeft:de weergave van negatieve getallen.

Het meest linkse bit wordt gelezen als het teken, positief of negatief, en de overige bits worden geïnterpreteerd volgens de standaard binaire notatie:van links naar rechts, plaats gewichten in veelvouden van twee.

Aanvulling

Hoe eenvoudig de benadering van tekengrootte ook is, het is niet erg praktisch voor rekenkundige doeleinden. Hoe voeg ik bijvoorbeeld een min vijf toe (1101₂ ) naar een ander getal, met behulp van de standaardtechniek voor binaire optelling?

Ik zou een nieuwe manier van optellen moeten uitvinden om het te laten werken, en als ik dat doe, kan ik het werk net zo goed doen met aftrekken met de hand; er is geen rekenkundig voordeel aan het gebruik van negatieve getallen om aftrekkingen uit te voeren door middel van optellen als we het moeten doen met tekengrootte-nummering, en dat was ons doel!

Er is een andere methode om negatieve getallen weer te geven die werkt met onze bekende techniek van optellen met de hand, en is ook logischer vanuit het oogpunt van plaatsgewogen nummering, complementatie genaamd.

Met deze strategie wijzen we het meest linkse bit toe om een ​​speciaal doel te dienen, net zoals we deden met de teken-magnitude-benadering, waarbij we onze aantallimieten net als voorheen definiëren. Deze keer is het meest linkse bit echter meer dan alleen een tekenbit; het bezit eerder een negatieve plaatsgewichtswaarde. Een waarde van min vijf wordt bijvoorbeeld als volgt weergegeven:

Met de drie rechtse bits die een grootte van nul tot zeven kunnen vertegenwoordigen, en de meest linkse bit die nul of min acht vertegenwoordigt, kunnen we met succes elk geheel getal vanaf min zeven weergeven (1001₂ =-8₁₀ + 1₂ =-7₁₀ ) tot positief zeven (0111₂ =0₁₀ + 7₁₀ =7₁₀ ).

Het vertegenwoordigen van positieve getallen in dit schema (waarbij het vierde bit wordt aangeduid als het negatieve gewicht) verschilt niet van dat van gewone binaire notatie. Het weergeven van negatieve getallen is echter niet zo eenvoudig:

Merk op dat de negatieve binaire getallen in de rechterkolom, zijnde de som van het totaal van de drie rechtse bits plus de min acht van het meest linkse bit, niet in dezelfde volgorde "tellen" als de positieve binaire getallen in de linkerkolom.

In plaats daarvan moeten de drie rechterbits op de juiste waarde worden ingesteld om gelijk te zijn aan het gewenste (negatieve) totaal wanneer opgeteld bij de negatieve waarde van acht plaatsen van het meest linkse bit.

Twee's complement

Die juiste drie bits worden het twee-complement van het overeenkomstige positieve getal genoemd. Overweeg de volgende vergelijking:

In dit geval, waarbij het negatieve gewichtsbit het vierde bit is (plaatswaarde van min acht), zal het complement van de twee voor elk positief getal de waarde zijn die nodig is om op te tellen bij min acht om het negatieve equivalent van die positieve waarde te maken.

Gelukkig is er een gemakkelijke manier om het complement van de twee voor elk binair getal te achterhalen:keer gewoon alle bits van dat getal om, verander alle enen in nullen en vice versa (om te komen tot wat het complement van de ene wordt genoemd) en voeg er dan een toe! Om bijvoorbeeld het twee-complement van vijf (101₂ ), zouden we eerst alle bits omkeren om 010₂ . te verkrijgen (de "one's complement"), voeg er dan een toe om 011₂ . te verkrijgen , of -5₁₀ in drie-bits twee-complementvorm

Interessant genoeg werkt het genereren van het twee-complement van een binair getal hetzelfde als je alle bits manipuleert, inclusief het meest linkse (teken) bit tegelijk met de magnitudebits. Laten we dit proberen met het eerste voorbeeld, een positieve vijf omzetten in een negatieve vijf, maar het complementatieproces uitvoeren op alle vier de bits.

We moeten er zeker van zijn dat het 0 (positieve) tekenbit op het originele getal wordt toegevoegd, vijf (0101₂ ). Eerst alle bits omkeren om het enen-complement te verkrijgen:1010₂ . Als we er dan één toevoegen, krijgen we het uiteindelijke antwoord:1011₂ , of -5₁₀ uitgedrukt in vier-bits, twee-complementvorm.

Het is van cruciaal belang om te onthouden dat de plaats van het negatieve-gewichtsbit al moet zijn bepaald voordat de twee-complementconversies kunnen worden uitgevoerd. Als ons binaire nummeringsveld zodanig was dat de achtste bit werd aangeduid als de bit met negatief gewicht (10000000₂ ), zouden we het complement van de twee moeten bepalen op basis van alle zeven andere bits.

Hier, de twee complement van vijf (0000101₂ ) zou 1111011₂ . zijn . Een positieve vijf in dit systeem wordt weergegeven als 00000101₂ , en een min vijf als 11111011₂ .

GERELATEERDE WERKBLAD:

• Werkblad binaire wiskunde