Herwaardering van de levensduurverdelingen van de luminescentie in silicium nanokristallen
Abstract
De luminescentiedynamiek in ensembles van nanokristallen wordt gecompliceerd door een verscheidenheid aan processen, waaronder de grootte-afhankelijkheid van de stralings- en niet-stralingssnelheden in inhomogene verbrede monsters en interdeeltjesinteracties. Dit resulteert in een niet-exponentieel verval, dat voor het specifieke geval van siliciumnanokristallen (SiNC's) op grote schaal is gemodelleerd met een Kohlrausch- of "uitgerekte exponentiële" (SE) -functie. We leiden eerst de populatievervalfunctie af voor een luminescentieverval volgend op exp[− (t /τ) β ]. We vergelijken vervolgens de verdelingen en gemiddelde tijden die zijn berekend door aan te nemen dat ofwel het luminescentieverval of het populatieverval deze functie volgt en laten zien dat de resultaten significant verschillend zijn voor β veel lager dan 1. Vervolgens passen we deze twee typen SE-functies en andere modellen toe op de luminescentievervalgegevens van twee thermisch gegroeide SiNC-monsters met verschillende gemiddelde groottes. De gemiddelde levensduur is sterk afhankelijk van de experimentele opstelling en het gekozen aanpassingsmodel, die geen van alle de dynamiek van het ensemble-verval adequaat lijken te beschrijven. Frequentie-opgeloste spectroscopie (FRS)-technieken worden vervolgens toegepast op SiNC's om de levensduurverdeling direct te extraheren. De snelheidsverdeling heeft een halve breedte van ~ 0,5 decennia en lijkt vooral op een enigszins hoogfrequente scheve lognormale functie. De combinatie van TRS- en FRS-methoden lijkt het meest geschikt om de luminescentiedynamiek van NC-materialen met een breed emissiespectrum bloot te leggen.
Inleiding
Colloïdale nanodeeltjes kunnen worden gebruikt in een groot aantal toepassingen, waaronder katalyse, medische behandelingen en opto-elektronische toepassingen [1,2,3,4]. Halfgeleider nanodeeltjes zijn van bijzonder belang voor lichtemissie, fotovoltaïsche en fotokatalytische toepassingen [5, 6]. Silicium-nanokristallen (SiNC's) staan momenteel in de belangstelling vanwege de afstembare emissie-eigenschappen [7], evenals de overvloed en biocompatibiliteit van silicium [8]. Om op nanodeeltjes gebaseerde technologieën te ontwikkelen, is een grondige kennis van de relevante opto-elektronische eigenschappen nodig, en tijdsopgeloste spectroscopie is hiervoor vaak een waardevol hulpmiddel.
De levensduur van de luminescentie van SiNC's wordt meestal gemodelleerd met een uitgerekte exponentiële (SE) functie met de basisvorm exp[ − (λt ) β ], waarbij de spreidingsparameter β heeft waarden tussen 0 en 1, λ is een snelheidsparameter, en t het is tijd. Deze functie wordt vaak beschreven als "langzamer dan exponentieel" en impliceert een asymmetrische verdeling van vervalsnelheden die naar een langere levensduur leiden. Zodra de β en λ parameters zijn gevonden door een luminescentie-vervalcurve aan te passen, de corresponderende vervalsnelheidsverdeling kan bij benadering worden gereconstrueerd [9].
Over de oorsprong van het SE-luminescentieverval in silicium en andere kwantumstippen van halfgeleiders is de afgelopen twee decennia hevig gedebatteerd, en het debat is recentelijk voortgezet [10]. Er zijn verschillende verklaringen voorgesteld voor het verschijnen van de SE in de vervaldynamiek, waaronder carrier-tunneling en trapping in dicht bij elkaar liggende ensembles van nanokristallen [11], de inhomogeen verbrede grootteverdeling [12], grootte-afhankelijke elektron-fononkoppeling [10] , en een verdeling van barrièrehoogten voor niet-stralingsrecombinatie [13], waarbij de laatste vergelijkbaar is met een eerdere suggestie voor poreus silicium [14]. Het is duidelijk dat kennis van de snelheidsverdeling vereist is voor een begrip van het luminescentiemechanisme in SiNC's en meer in het algemeen in halfgeleider nanokristallen.
In veel van de eerdere literatuur over SiNC's werd het uitgerekte exponentiële verval a priori aangenomen, meestal zonder analyse van andere mogelijke distributies. De SE heeft de neiging om visueel goed te passen (d.w.z. de best passende lijn lijkt "met het oog" goed overeen te komen met de gegevens). Bovendien is er in de overgrote meerderheid van de eerdere werken, bijvoorbeeld [15], onduidelijkheid over de vraag of het populatieverval of het luminescentieverval daadwerkelijk wordt gemodelleerd. Deze zijn gerelateerd aan een afgeleide en men moet de juiste uitdrukking gebruiken om de vervaltijdschalen in de steekproef te begrijpen [16]. Ook kan de responsiviteitsfunctie van de detector een significant effect hebben op de gemeten luminescentie-vervalcurve in SiNC's, vanwege het brede ensemble-emissiespectrum. Desondanks is er zelden of nooit rekening gehouden met de responsiviteit, waardoor het moeilijk is om resultaten van verschillende onderzoeken met elkaar te vergelijken. Ten slotte hebben geen eerdere studies geprobeerd om frequentie-opgeloste spectroscopie (FRS) te gebruiken bij de analyse van silicium nanokristallen. In principe staat FRS toe dat de levensduurverdeling wordt geëxtraheerd zonder a priori een model aan te nemen.
Het doel van dit artikel is om een benadering vast te stellen voor het meten, modelleren en interpreteren van de luminescentiedynamiek van silicium nanokristallen. Gehoopt wordt dat dit kan helpen om de enorme diversiteit aan vaak tegenstrijdige resultaten in de literatuur beter te begrijpen, tot betere overeenstemming, of op zijn minst meer consistentie, tussen verschillende metingen, en om de luminescentiemechanismen beter te begrijpen.
Basistheorie
We vergelijken drie modellen:de uitgerekte exponentiële, die veel wordt gebruikt voor Si-nanokristallen, de lognormale vervalverdeling, die onlangs voor het eerst werd toegepast op SiNC's [17], en het bimoleculaire verval. Voor elk model is de emissiewaarschijnlijkheidsdichtheidsfunctie, weergegeven door de integraal van de intensiteitsfunctie g (t ), op het moment t′ is gerelateerd aan de fractie van excitaties die overblijven bij t′ volgens [16].
$$ {\int}_0^tg\left({t}^{\hbox{'}}\right) dt=1-\frac{c_t}{c_0}, $$ (1)waar c t en c 0 zijn het aantal opgewonden NC's op het moment t en aanvankelijk. De kansdichtheidsfunctie beschrijft de fractie fotonen die wordt uitgezonden tussen tijd 0 en t ten opzichte van het totaal aantal uitgezonden fotonen. Als het populatieverval een eerste-orde-snelheidsvergelijking volgt (d.w.z. "monomoleculaire" recombinatie), hebben we dc t /dt = − λc t , waar λ = 1/τ 0 , wat leidt tot de gebruikelijke c t /c 0 = exp[− λt ] en g (t ) = λ⋅ exp[− λt ] na het nemen van de tijdsafgeleide van beide zijden van Vgl. 1. De afgeleide is nodig omdat de luminescentie-intensiteit gemeten in het venster dt′ is evenredig met de verandering in de aangeslagen fractie over dat interval.
Als we zowel stralings- als niet-stralingssnelheden beschouwen, dan vervangen we de totale vervalsnelheid λ met λ R + λ NR zodat g (t ) = (λ R + λ NR )exp[− (λ R + λ NR t ] = λ R exp[− (λ Ri + λ NR )t ] + λ NR exp[− (λ R + λ NR )t ] waarin alleen de eerste term meetbaar is, wat een gemeten intensiteit oplevert voor tijdopgeloste spectroscopie (TRS) gegeven door
$$ g(t)={\lambda}_R\exp \left[-\left({\lambda}_R+{\lambda}_{NR}\right)t\right]. $$ (2)De vervalfunctie die wordt gebruikt om de gegevens te passen, I t = A· exp(− λt ) + dc, schalen met een extra willekeurige prefactor, A , die afhangt van de detectie-efficiëntie en het aantal geëxciteerde nanodeeltjes en zal leiden tot de juiste schaal. Een dc-offset wordt gewoonlijk toegevoegd aan de Decay-functie als een andere passende parameter.
In het geval van het uitgerekte exponentiële verval, vervalt de fractie aangeslagen emitters volgens
$$ \frac{c_t}{c_0}=\exp \left[-{\left({\lambda}_{SE}t\right)}^{\beta}\right]. $$ (3)waar λ SE is de uitgerekte exponentiële vervalsnelheid (gelijk aan 1/τ SE ). Dit invoegen in Eq. 1 en het nemen van de afgeleide van beide zijden zoals eerder levert een emissiewaarschijnlijkheidsfunctie op gegeven door
$$ g(t)={\beta \lambda}_{SE}^{\beta }{t}^{\beta -1}\exp \left[-{\left({\lambda}_{SE} t\right)}^{\beta}\right]. $$ (4)Een manier om de verdeling van frequenties te schatten H (λ ) die leidt tot Vgl. 3 werd getoond met behulp van een inverse Laplace-transformatie [9], wat een verdeling opleverde die groter wordt met afnemende β en is scheef in de richting van hoge frequenties.
Helaas, in vgl. 4, is het niet mogelijk om de prefactor te scheiden in stralende en niet-stralende delen. Dit betekent dat vgl. 4 is alleen correct genormaliseerd voor λ NR = 0 [16], en de levensduurverdeling verkregen uit een PL-vervalcurve wordt alleen op deze manier begrepen. Bovendien is er een tijdsafhankelijke term in de prefactor; daarom heeft het populatieverval een andere tijdsafhankelijkheid dan het luminescentieverval [16, 18]. Om waarden van τ . te verkrijgen SE en β voor het populatieverval waaruit de juiste gemiddelde levensduur kan worden afgeleid, moet men Vgl. 4 om het waargenomen verval te modelleren, waarbij we g . vervangen (t ) door de gemeten vervalfunctie I t :
$$ {I}_t=A{\beta \lambda}_{SE}^{\beta }{t}^{\beta -1}\exp \left[-{\left({\lambda}_{SE }t\right)}^{\beta}\right]+\mathrm{dc}. $$ (5)In verg. 5, een schaalparameter (die ook de β . kan absorberen en λ termen in de prefactor) en een dc-offset werden ingevoegd als aanpassingsparameters. De gemiddelde levensduur wordt gegeven door
$$ \left\langle {\tau}_{SE}\right\rangle =\frac{\tau_{SE}}{\beta}\Gamma \left[\frac{1}{\beta}\right], $$ (6)waar Γ vertegenwoordigt de Gamma-functie, en de gemiddelde vervaltijd is
$$ \left\langle t\right\rangle ={\tau}_{SE}\frac{\Gamma \left(2/\beta \right)}{\Gamma \left(1/\beta \right)} . $$ (7)In veel eerder werk was het gebruikelijk om de "standaard" uitgerekte exponentiële exp[− (λ SE t ) β ] om het luminescentieverval te modelleren in plaats van het populatieverval. Dienovereenkomstig hebben we een genormaliseerde intensiteitsfunctie gegeven door
$$ g(t)=\frac{\lambda_{SE}\beta }{\Gamma \left(1/\beta \right)}\exp \left[-{\left({\lambda}_{SE} t\right)}^{\beta}\right]. $$ (8)Vergelijking 8 is genormaliseerd zodat integratie tussen t = 0 en ∞ is gelijk aan 1. Het bijbehorende aanpasmodel is eenvoudig
$$ {I}_t=A\exp \left[-{\left({\lambda}_{SE}t\right)}^{\beta}\right]+\mathrm{dc}. $$ (9)Vergelijking 9 wordt veel toegepast en past vaak redelijk goed bij de SiNC-luminescentiegegevens, ondanks het feit dat (zoals Vgl. 4) Vgl. 8 is strikt genormaliseerd voor een absolute kwantumefficiëntie (AQY) van 100%. Een vaak over het hoofd gezien punt is het feit dat men τ . niet kan extraheren SE (=1/λ SE ) en β van het luminescentieverval gemodelleerd door Vgl. 9 en gebruik ze om de gemiddelde tijden te berekenen met Vgl. 6 en 7. In wezen, Vgl. 4 en 8 zijn verschillende intensiteitsvervalmodellen en men zou verschillende populatievervalfuncties, gemiddelde tijden en vervalsnelheidsverdelingen moeten verwachten.
Om het populatieverval te vinden dat zou leiden tot een intensiteitsfunctie gegeven door Vgl. 9, passen we hetzelfde proces toe dat we hebben gedaan om van Vgl. 4 naar vgl. 5, maar omgekeerd, dat wil zeggen:
$$ \frac{c_t}{c_0}=1-\frac{\lambda_{SE}\beta }{\Gamma \left(1/\beta \right)}{\int}_0^t\exp \left[ -{\left({\lambda}_{SE}t\right)}^{\beta}\right]\cdot \mathrm{dt}. $$ (10)Na verschillende stappen is de oplossing voor Vgl. 10 is
$$ \frac{c_t}{c_0}=\frac{1}{\Gamma \left(1/\beta \right)}\Gamma \left[1/\beta, {\left({\lambda}_{ SE}t\right)}^{\beta}\right]. $$ (11)Vergelijking 11 is het populatieverval verkregen uit het intensiteitsverval gegeven door Vgl. 8. Het op de gebruikelijke manier vinden van de gemiddelde levensduur leidt tot
$$ \left\langle {\tau}_{SE}\right\rangle ={\tau}_{SE}\frac{\Gamma \left(2/\beta \right)}{\Gamma \left(1 /\beta \right)} $$ (12)en een gemiddelde vervaltijd van
$$ \left\langle t\right\rangle ={\tau}_{SE}\frac{\Gamma \left(3/B\right)}{2\Gamma \left(2/\beta \right)} . $$ (13)Ten slotte is de frequentieverdeling (1 /λ )·H (λ ), waar, zoals eerder, H (λ ) is de verdeling berekend in ref. [9] voor een populatieverval gegeven door Vgl. 3. Deze resultaten zijn samengevat in Tabel 1.
De verschillen tussen de twee SE-formules zijn significant (Fig. 1). In de literatuur vindt men vaak dat het intensiteitsverval wordt gemodelleerd door A· exp[− (t /τ SE ) β ] + dc (d.w.z. Vgl. 9) en vervolgens worden de gemiddelde tijden berekend met Vgl. 6 en 7. Dit lijkt wiskundig onjuist te zijn, aangezien Vgl. 6 en 7 zijn afgeleid van een intensiteitsverval gegeven door Vgl. 4, niet vgl. 8. Neem bijvoorbeeld τ SE = 100 μs en β = 0,7, zoals weergegeven in Fig. 1, voor een intensiteitsverval gegeven door exp[− (t /τ SE ) β ], vinden we een gemiddelde tijdconstante van 199 s (Vgl. 12), vergeleken met 127 μs bij gebruik van Vgl. 6. Vergelijkbare verschillen worden gevonden voor de gemiddelde vervaltijden (Vgl. 7 en 13). Bovendien is er een benadering die bekend staat als de Higashi-Kastner-methode voor het schatten van een karakteristieke levensduur [19], die is toegepast op SiNC's als alternatief voor het toepassen van het SE-vervalmodel [20, 21]. In dit model is de karakteristieke vertragingstijd, t d , wordt eenvoudigweg genomen als de piek van de vervalgegevens, uitgezet als I t ·t vs. t . Er werd gesuggereerd dat dit equivalent is aan (1 /β ) 1 /β ·τ SE verkregen van vgl. 9 [20].
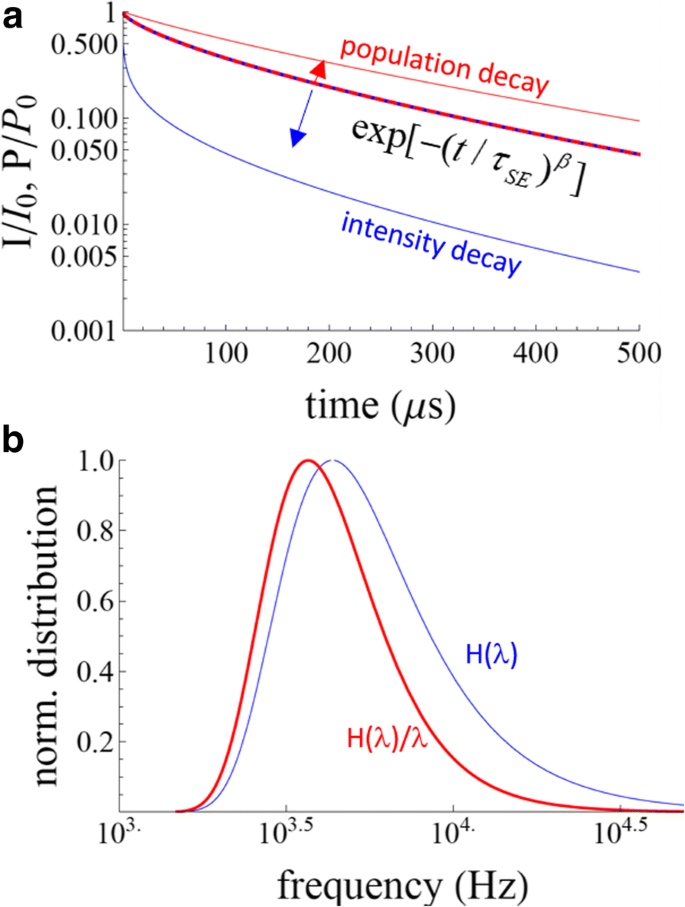
Gestrekte exponentiëlen. een Bevolking en intensiteit nemen af voor de uitgerekte exponentiële functie met τ SE = 100 μs en β = 0,7. De blauw-rode stippellijn is exp[− (het ) β ]. Als dit het populatieverval vertegenwoordigt, wordt het intensiteitsverval weergegeven door de blauwe lijn. Als exp[− (het ) β ] het intensiteitsverval is, dan wordt het bevolkingsverval weergegeven met de rode lijn. b De bijbehorende tariefverdelingen
Als alternatief kan de verdeling van de vervalsnelheden een specifieke Η . volgen (λ ), wat leidt tot een luminescentieverval gegeven door:
$$ g(t)={\int}_0^{\infty}\mathrm{H}\left(\lambda \right)\cdot \exp \left(-\lambda t\right)\mathrm{d}\ lambda, $$ (14)waar Η (λ ) vertegenwoordigt de frequentieafhankelijke verdeling van vervalsnelheden. Vergelijking 14 reduceert tot Vgl. 2 als Η (λ ) is gelijk aan de Dirac-deltafunctie δ (λ − λ 0 ), of het kan een continue reeks exponentiële getallen vertegenwoordigen, gewogen door de geselecteerde verdeling. Een lognormale functie lijkt een redelijke keuze in nanokristalsystemen, aangezien veel nanokristallensembles van nature lognormale grootteverdelingen volgen [22]. Om verdere verwarring te voorkomen, gebruiken we de standaard genormaliseerde definitie van lognormale functie gegeven door:
$$ H\left(\lambda \right)=\frac{1}{\lambda}\cdot \frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{\ left(\ln \lambda -\mu \right)}^2}{2{\sigma}^2}\right]. $$ (15)zodat de gemeten vervalfunctie is
$$ {I}_t=A\cdot {\int}_0^{\infty}\left(\frac{1}{\lambda}\cdot \frac{1}{\sigma \sqrt{2\pi }} \exp \left[-\frac{{\left(\ln \lambda -\mu \right)}^2}{2{\sigma}^2}\right]\cdot \exp \left(-\lambda t \rechts) d\lambda \rechts)+ dc. $$ (16)Net als bij de SE-functie zijn er slechts twee onafhankelijke variabelen (evenals een offset en een schaalfactor). De momenten zijn zoals gebruikelijk gedefinieerd; d.w.z. de mediane koers wordt gegeven door exp (μ ), het gemiddelde van exp (μ + σ 2 /2), en de meest waarschijnlijke levensduur (de piek van de verdeling) is exp (μ − σ 2 ). Voorheen werd een niet-standaardverdeling gebruikt [16] (d.w.z. een verdeling die, hoewel op zichzelf geldig, niet de algemeen aanvaarde lognormale verdelingsfunctie is). Vergelijking 14 is ook van toepassing op een stralingsvervalverdeling (d.w.z. AQY = 100%). Er is zelfs gesuggereerd dat vervalsnelheidsverdelingen worden gewogen door een (onbekende) kwantumefficiëntiefunctie [16]. In reële situaties moet men dit voorbehoud gewoon accepteren, aangezien het moeilijk of onmogelijk is om de populatieverdeling van niet-stralingssnelheden in de steekproef te kennen.
Luminescentieverval kan ook overeenkomen met een tweede-ordereactie (d.w.z. het "bimoleculaire" verval) [23]. Hier wordt de snelheid waarmee de populatie vervalt gegeven door dc /dt = − λ [c t ] 2 , wat een resterende fractie c . oplevert t /c 0 = (c 0 het + 1) −1 . Het invoegen van deze uitdrukking in Vgl. 1 resulteert in een verval van de machtswet:
$$ {I}_t/{I}_0=A\frac{\lambda {c}_0}{{\left(\lambda {c}_0+1\right)}^2}. $$ (17)Het bimoleculaire model heeft slechts één snelheidsconstante λ (in tegenstelling tot de uitgerekte exponentiële en lognormale, die verdelingen van snelheden hebben), en er is geen gemiddelde levensduur. Meer specifiek divergeert de tijdintegraal en is de gemiddelde levensduur van het tweede-ordeverval oneindig.
De "standaard" SE-functie (Vgl. 9) is verreweg het dominante model dat is gebruikt voor SiNC-luminescentieverval, met veel artikelen gewijd aan het interpreteren van de betekenis van het verval voor de luminescentiemechanismen. De lognormale levensduurverdeling werd vrij recent voor het eerst toegepast op SiNC's [17, 24, 25]. Het is duidelijk dat er a priori weinig reden is om een model aan te nemen, en het zou in plaats daarvan de voorkeur hebben om de verdeling van vervalsnelheden direct vast te stellen. Dit kan in principe in ieder geval worden bereikt door kwadratuurfrequentie-opgeloste spectroscopie (QFRS), die meermaals is toegepast op amorf silicium, maar niet op SiNC's.
Kwadratuur frequentie-opgeloste spectroscopie
De QFRS-methode wordt nogal schaars beschreven in de literatuur, voornamelijk beperkt tot enkele studies van met zeldzame aarde gedoteerde glazen [26,27, en a-SiOx:H
Het kwadratuur FRS-signaal wordt gecompliceerd door het feit dat een enkel exponentieel verval niet resulteert in een deltafunctie in het QFRS-spectrum. Het waargenomen signaal is in feite de convolutie van de levensduurverdeling met een enkele exponentiële responsfunctie gegeven op een logschaal met [31].
$$ {S}_{\log_{10}\mathrm{r}}=\frac{{\omega \tau}_0}{1+{\omega}^2{\tau}_0^2}, $$ (18)Waar de tijdconstante τ 0 = ω 0 −1 . Dus, tenzij de verdeling van de vervalsnelheid meerdere decennia breed is, moet een deconvolutie worden uitgevoerd om een zinvolle verdeling te extraheren.
Resultaten en discussie
Basiskarakterisering
Vanwege het lage contrast geassocieerd met de SiNC's en het overlappende gevlekte contrast van de amorfe koolstofdrager, kunnen computergebaseerde algoritmen voor het tellen van deeltjes die gebruikmaken van helderveldbeelden niet worden toegepast en moesten de diameters "met het oog" worden geschat met behulp van pixeltelsoftware ( voorbeeld helderveld TEM-afbeeldingen worden getoond in Fig. 2a, d en de handmatige deeltjestellingsresultaten werden aangepast aan een lognormale verdeling (Fig. 2c, f) om een lineaire gemiddelde diameter van 2,9 nm te verkrijgen (gemiddelde en standaarddeviatie van de natuurlijke logaritmen μ = 1.057 en σ = 0.1555) en 5,4 nm (μ = 1.663 en σ = 0.1917), voor respectievelijk 1100 en 1200 °C gloeitemperaturen. Deze monsters worden voortaan "kleine" en "grote" SiNC's genoemd. De afmetingen werden verder gecontroleerd door beeldvorming met hoge resolutie van geselecteerde NC's (Fig. 2b, e), waarbij de roosterranden konden worden gebruikt als een andere manier om de NC's te identificeren en hun diameters te schatten. De Fourier-transformatie infrarood (FTIR) spectroscopie en XPS-gegevens toonden aan dat de voorbereide SiNC's met succes werden gefunctionaliseerd met dodeceen; de kleine SiNC's zijn echter meer geoxideerd dan de grote en vertonen dus een kleinere mate van functionalisering (Aanvullend bestand 1:Figuren S1 en S2).
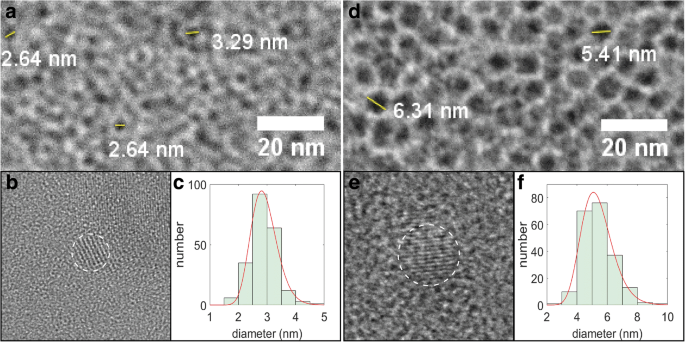
TEM-afbeeldingen van SiNC's. een Helderveld, b hoge resolutie, en c grootteverdelingshistogram voor de kleine SiNC's. Panelen d –f vertegenwoordigen een vergelijkbare reeks afbeeldingen van de grote SiNC's
Fotoluminescentie en tijdopgeloste spectroscopie
De fotoluminescentie (PL) spectra waren gecentreerd op 660 en 825 nm met een maximum over de volledige breedte van 123 en 198 nm voor respectievelijk kleine en grote SiNC's (inzet van figuur 3). De indirecte bandgap-energieën zijn voorspeld 1,87 en 1,37 eV volgens \( {E}_g\kern0.5em =\kern0.5em \sqrt{E_{g,\mathrm{bulk}}^2\kern0.5em +\ kern0.5em D/{R}^2} \) [32] met D = 4.8 eV 2 /nm 2 en R zijnde de NC-straal, die nauw overeenkomt voor de kleine deeltjes, maar een iets kleinere bandgap voorspelt dan verkregen door de PL-piek voor de grote. De AQY was 12% voor de kleine SiNC-steekproef en 56% voor de grote NC's. Onafhankelijke metingen op een ander systeem leverden 18% en 48% op voor de twee monsters, wat typerend is voor de onzekerheden in AQY-metingen [33] voor de verschillende excitatie- en afsnijgolflengten. We veronderstellen dat de minder gekromde, lager-energetische oppervlakken van de grotere NC's leiden tot een betere oppervlaktefunctionalisering en een kleinere bijdrage van niet-stralende oppervlaktetoestanden aan het algehele PL-spectrum.
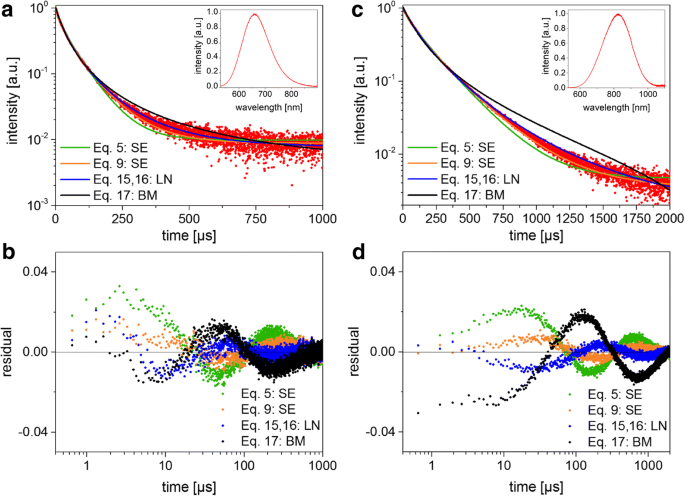
TRS-gegevens en aanpasresultaten. een Luminescentie vervalt en de bijbehorende pasfunctie (BM bimoleculair, SE uitgerekt exponentieel, LN lognormaal) voor kleine SiNC's. Het PL-spectrum wordt weergegeven in de inzet. b Residuplots voor de passingen in (a , c , d ) tonen de curven en residuen voor de grote SiNC's.
Beide monsters leverden een niet-exponentieel verval op, zoals verwacht op basis van de uitgebreide eerdere literatuur over SiNC's. De gemeten PL-vervallen waren geschikt voor vergelijkingen. 5, 9, 16 en 17 om de verschillende modellen te testen met behulp van standaard som-van-kwadratenminimalisatie (Fig. 3). Het feit dat de detectorresponsiviteit niet constant is over het brede NC-luminescentiespectrum zal later worden besproken. Voor alle gevallen oscilleren de residuen, wat aangeeft dat geen van de modellen volledig adequaat lijkt, maar het "eenvoudige" SE-model (Vgl. 9) en de lognormale (Vgl. 16) neigen naar de laagste kwadratensom van de residuen. De berekende aanpassingsparameters en gemiddelde levensduur voor de twee SiNC-monsters worden weergegeven in Tabel 2, waarin de gemiddelden duidelijk afhankelijk zijn van de selectie van het vervalmodel. De Higashi-Kastner-methode werd ook toegepast (Fig. 4) en de piekposities werden bepaald door de vertragingstijdcurves aan te passen aan een scheve Gaussian. De Higashi-Kastner-methode levert een tijdconstante op t d vrij gelijkaardig aan (1 /β ) 1 /β ∙τ SE , met deze waarden van Vgl. 9 zoals eerder getoond [20]. Het bimoleculaire model past redelijk slecht, in overeenstemming met geïsoleerde nanokristallen die niet zwaar over-geëxciteerd zijn. Het wordt daarom niet verder besproken.
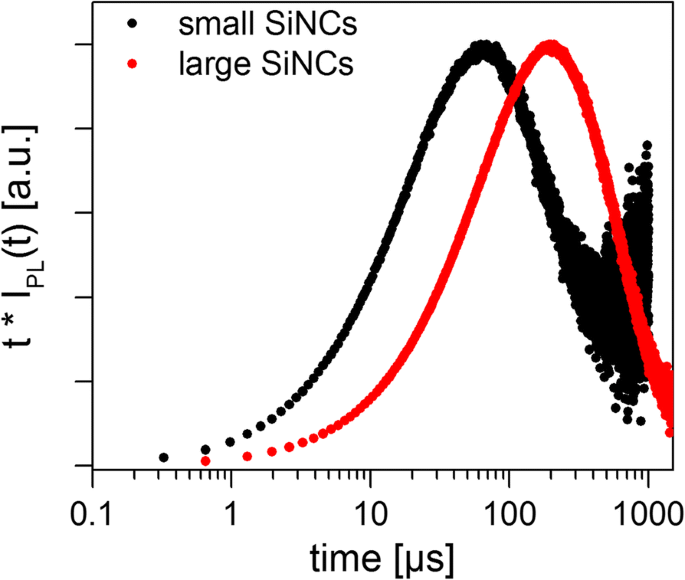
Genormaliseerde PL-vervalcurves vermenigvuldigd met de vervaltijd (Higashi-Kastner-plots) voor de kleine en grote SiNC-ensembles. De piekposities vertegenwoordigen de meest dominante vervaltijd, weergegeven door t d in tabel 2
Om het gemiddelde aantal excitonen per NC voor deze meetomstandigheden te schatten, moet de excitatiesnelheid worden berekend uit de absorptiedoorsneden, die duidelijk kan oplopen tot 10 −14 cm 2 voor deze experimenten [34]. Gegeven een excitatiestraling van 4500 W/m 2 bij 352 nm en de gemeten piekemissiesnelheden (zie de volgende paragrafen), werd het aantal excitaties per NC voor de grote en kleine SiNC's geschat op minder dan respectievelijk ~ -1 en 0,2. Dit suggereert dat de grote SiNC's mogelijk iets te opgewonden zijn. Dit kan extra niet-stralingseffecten veroorzaken vanwege de aanwezigheid van multi-excitonen in sommige NC's. Om deze mogelijkheid verder te evalueren, werd de levensduur gemeten als een functie van het excitatievermogen; tot 2% van de hierboven vermelde waarden. De resultaten vertoonden geen trend en waren altijd hetzelfde binnen ~ 2% (aanvullend bestand 1 figuur S3), wat dicht bij de montage- en herhaalbaarheidsfouten ligt, ondanks de lage signaal-ruisverhouding in de low-power metingen. De mogelijke over-excitatie van de NC's lijkt dus weinig effect te hebben op de resultaten.
Om de levensduurverdeling van TRS te schatten, werden de vervalsingen gemeten over een reeks vaste golflengten met behulp van een monochromator met een banddoorlaat van ~-3 nm (Fig. 5). Vanwege de lage intensiteit werd hiervoor een fotonen tellend PMT-systeem gebruikt. Met effectief monochromatische straling zou er geen verschil moeten zijn in de vervalconstanten gemeten met verschillende detectoren, aangezien er een verwaarloosbare verdeling van de responsfunctie is over zo'n smal bereik van golflengten. Dezelfde trend werd gevonden voor de dodecyl-getermineerde deeltjes zoals waargenomen in andere silicium-NC's [25, 35, 36]; dat wil zeggen, de dispersieparameter neemt dichter bij de eenheid toe en de levensduur neemt snel toe als functie van de golflengte (Fig. 5, Tabel 3).
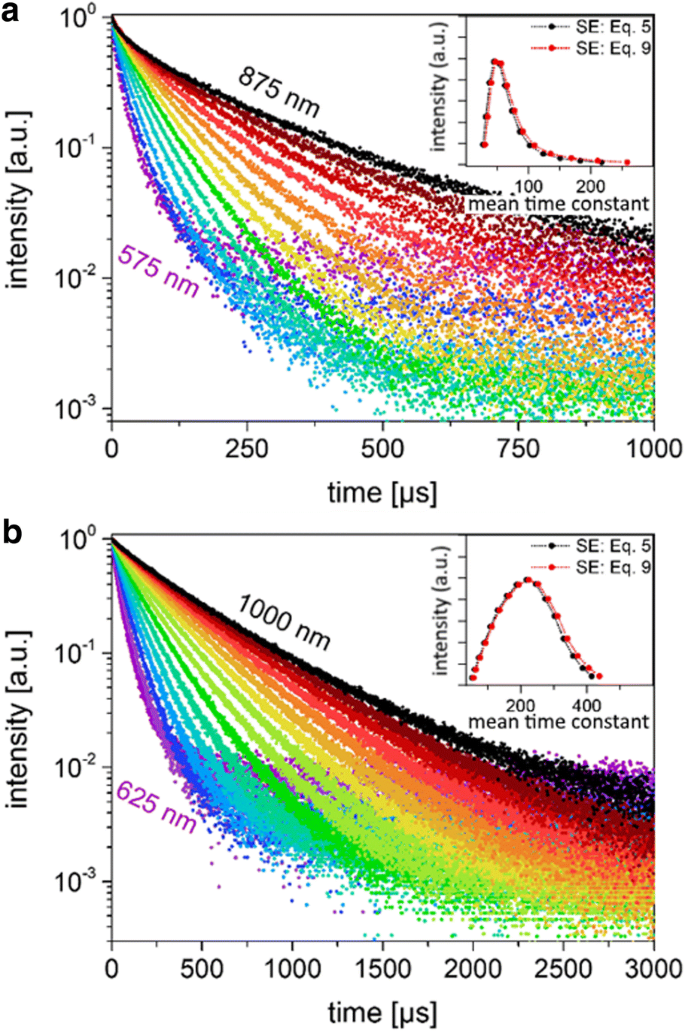
Smalle golflengte PL vervalt. een Luminescentie vervalt voor de kleine SiNC's bij specifieke emissiegolflengten (3 nm FWHM) variërend van 575 tot 875 nm, in intervallen van 25 nm. De gegevens waren geschikt voor vergelijkingen. 5 en 9, wat een bijna enkele exponentiële fit opleverde. b Luminescentie vervalt bij specifieke emissiegolflengten variërend van 625 tot 1000 nm voor de grote SiNC's die onder dezelfde omstandigheden zijn gemeten en gemonteerd. De resulterende tijdconstanten voor de kleine en de grote SiNC's worden gegeven in Tabel 1
De kleinere deeltjes hadden altijd een kortere levensduur dan de grotere bij dezelfde meetgolflengte. Deze waarneming is consistent met de lagere AQY van de kleinere deeltjes, wat aangeeft dat de levensduur van de grote NC's minder sterk wordt bepaald door niet-stralingsprocessen. De grote NC's zijn ook minder geoxideerd in vergelijking met het kleine NC-monster (aanvullend bestand 1 figuur S1). Dus, hoewel de waarneming van de lagere AQY op het kleine monster consistent is met de gemeten kortere levensduur, kan men geen relatieve vergelijking maken van de twee monsters via golflengteselectie (in principe hangt de emissiegolflengte af van de grootte en de oxidatiegraad [24], die in de twee monsters verschillend is).
Ook uitgezet als inzetstukken in Fig. 5 zijn de verdelingen die zijn verkregen door het uitzetten van de gemiddelde levensduur die is verkregen uit de gemonochromateerde gegevens, met behulp van Vgl. 5 of 9 om de gegevens te passen, als functie van de PL-intensiteit bij die golflengte. Aangezien voor dit verval de bètaparameter redelijk dicht bij 1 ligt, is er vrij weinig verschil tussen de gemiddelde levensduur berekend met de twee versies van het SE-model en lijken de op deze manier verkregen verdelingen vergelijkbaar. Hoewel deze vervalsingen niet de "echte" verdeling van levens vertegenwoordigen vanwege niet-stralingsbijdragen aan I PL , kunnen ze toch een indicatie geven van de levensduurverdeling. Voor de kleine deeltjes zien we een piek bij ~ 47 s, terwijl voor de grote NC's de piek meer symmetrisch is en gecentreerd rond 220 μs.
Frequentie-opgeloste spectroscopie
We begonnen met het valideren van de FRS-gegevens van twee teststandaarden:de eerste was een RC-circuit en de tweede was een monster van fluorescerende Eu-chelaat-gedoteerde microsferen (Fisher Scientific). Het RC-circuit heeft een mono-exponentieel verval waarin de FRS-gegevens overeenkwamen met Eq. 9 vrij dicht en piekte op 12,7 kHz, in overeenstemming met de gemeten vervaltijdconstante van 78,9 s. Het Eu-chelaat PL-spectrum piekte bij 650 nm met een vervaltijd in de orde van honderden microseconden, wat een standaard vormt voor de Si NC's. De luminescentie nam ook bijna mono-exponentieel af met een levensduur van 670 s. De FRS-gegevens waren gecentreerd op ~-1570 Hz met een breedte die vrijwel gelijk was aan de responsfunctie (Vgl. 18), wat redelijk dicht bij het waargenomen TRS-resultaat ligt. Het verschil (636 vs. 670 s) kan te wijten zijn aan het enigszins niet-exponentiële gedrag van het verval gekoppeld aan de excitatiemethode, zoals hieronder verder wordt besproken.
De FRS-gegevens voor de Si-NC's zijn problematisch omdat de waargenomen QFRS-resultaten slechts iets breder bleken te zijn dan de responsfunctie (zie de inzet bij figuur 6a). Daarom moet een deconvolutie worden uitgevoerd op de gegevens, die bijna vrij van ruis moeten zijn om significante problemen met de deconvolutieprocedure te voorkomen. We gebruikten de Richardson-Lucy deconvolutiemethode [37] om een positiviteitsbeperking af te dwingen. De gedeconvolueerde en genormaliseerde QFRS-gegevens leveren vervolgens de gemeten levensduurverdeling direct op, zoals weergegeven in Fig. 6 voor respectievelijk de grote en kleine NC's (rode punten), zonder a priori een model aan te nemen. Voor beide steekproeven vinden we een brede levensduurverdeling die, in het geval van de grote NC's, enigszins scheef is in de richting van hogere frequenties, terwijl de kleine NC's-verdeling meer bijna symmetrisch is op een semilog-plot. De verdeling van de vervalsnelheid piekte bij 19.900 Hz (50,3 s) voor de kleine NC's, terwijl voor de grotere NC's de verdeling een piek bereikte bij 6280 Hz (159,2 μs).
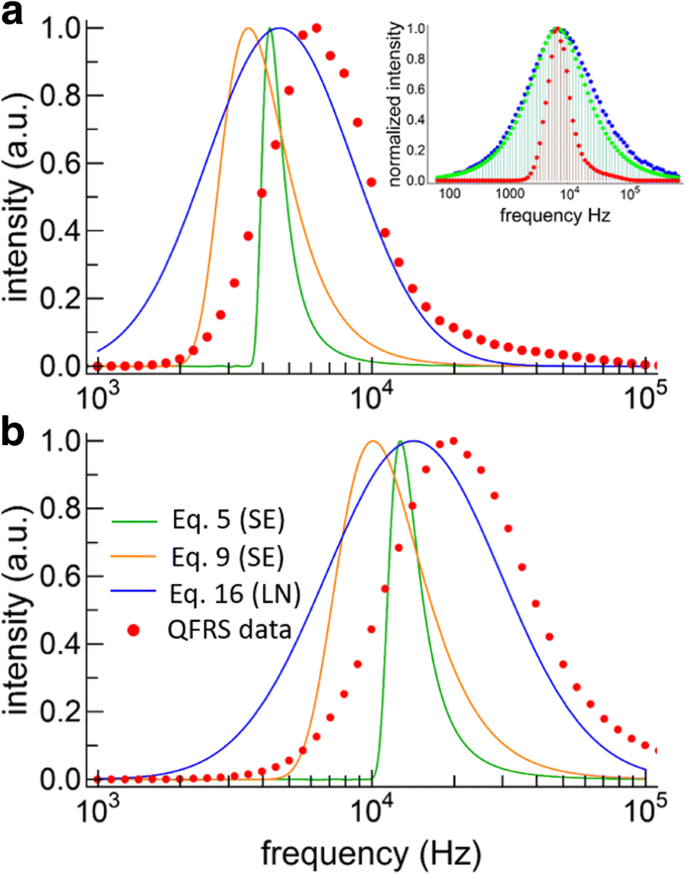
Lifetime distributions. een Lifetime distributions for large SiNCs obtained from fitting the TRS data with the two SE models and the LN model. The deconvolved QFRS data is also shown (red points). The inset shows the raw QFRS data for this sample (blue), the response function (green), and the deconvolution (red). b Lifetime distributions obtained by model fitting the TRS data (lines, same color scheme for both graphs) and QFRS (red points) for the small SiNCs
The lifetime distributions obtained from the stretched exponentials (orange and green curves) and lognormal (blue curve) model fits are also plotted in Fig. 6 for the large and small particles. The three decay models yield different distributions, both in terms of the overall shape and the peak frequencies. For both samples, the QFRS peaks at a higher frequency than any of the TRS model fits. While this may seem surprising, the same effects have been observed for CdSe NCs having a distribution of lifetimes [38, 39]. In fact, the TRS decay curve for CdSe NCs was evidently sensitive to the pulse duration, with shorter pulses accentuating the shorter lifetimes and the opposite case for long pulses. Furthermore, the mean lifetimes obtained by long-pulse duration techniques were a factor of 3–4 times longer than those obtained by phase measurement, which was due to preferential excitation of the long-lived population in steady-state excitation [38]. Indeed, the response function for TRS with a slow repetition rate is narrower than for FRS, cutting off especially sharply on the high frequency side [29]. Essentially, FRS accentuates the short-lived components of the ensemble decay more than steady-state TRS does, and this may account for the difference in the peak frequencies obtained by TRS model fitting and FRS. Despite these inherent differences, FRS appears suited to uncovering the distribution of lifetimes in ensembles of SiNCs, because it is obtained by direct measurement rather than by an assumed model. For SiNCs typical of a thermally grown ensemble, the main drawback of FRS is the necessity of a deconvolution.
While the detector response function certainly affects the QFRS, it plays a role in the TRS data as well. Indeed, measuring the ensemble decay with the APD vs. the PMT setup yielded mean decay times that were different by a factor of ~ 2, regardless of the fitting model applied. The detector responsivity also affects choice of the TRS “best” model fit. As mentioned above, our Thorlabs APD responsivity peaks at 600 nm, whereas for our Hamamatsu PMT the responsivity maximizes at 850 nm, in the long-wavelength, slow-decay part of the SiNC spectrum. Although apparently not reported before in the literature on SiNCs, this issue means that wide-spectrum TRS results from different setups are not comparable. Unfortunately, despite some critical conclusions, ref. [38] also used different detectors to compare the decay dynamics from the same wide-band NC sample and the response functions may not have been the same. Fortunately, however, the phase measurements and the steady-state measurements used the same detector (as was the case here) and the differences in the observed dynamics for these situations remain valid. Finally, the detector response function is in principle correctable in the FRS data if the responsivity curve and monochromated decay rate distribution are known over a wide range of wavelengths (i.e., decay rates). The responsivity correction has no such simple solution with TRS alone.
Conclusies
The most common models used for SiNC luminescence decay were described theoretically. The population decay corresponding to the “simple” stretched exponential luminescence decay, exp[− (t /τ ) β ], was derived and expressions for the characteristic mean times were found. This model was compared against the alternative model in which the population decays according to the simple SE. Two dodecene-functionalized SiNCs samples were then prepared from thermal nucleation and growth, followed by etching and alkane surface functionalization. These samples consisted of particles with mean diameters of 2.9 and 5.4 nm, respectively. The basic PL spectrum and TRS was measured using standard methods. The TRS data were fit with several distributions in order to establish whether any of them can be considered “true” and to find which one yields the best fit. While the simple SE luminescence decay fits the TRS data reasonably well, the distribution of residuals shows that it is not strictly accurate. None of the fitting models fully captures the shape of the measured decay rate distribution; they also show large deviations in the peak position and the shape of the distribution, as well as disagreement in the average time constants. Furthermore, the ensemble mean time constants were dependent on the responsivity curve of the detection system. This leads to serious questions about how to interpret the PL decay from ensembles of thermally-grown SiNCs.
Quadrature frequency-resolved spectroscopy was then employed with the intent to find the lifetime distribution directly for SiNC ensembles formed by thermal annealing of a base oxide. The spectrum was found to be not much wider than the intrinsic QFRS response function, requiring a deconvolution in order to extract the SiNC rate distribution. This yielded a distribution whose shape was nearly symmetrical (on a semilog scale) for the small NC sample and about half a decade wide, whereas it was slightly more skewed for the large NCs. We find that FRS techniques are suited to the study of SiNC luminescence dynamics and, after deconvolving the system response from the data, FRS yields the decay rate distribution directly. The most significant problem is the required deconvolution, but the Richardson-Lucy method was found to produce fairly robust results. While the detector response function can in principle be corrected from the FRS data, there is no simple means to do this for wide-PL-band TRS data. Still, as long as the data compared are from the same detector then the results should at least be internally meaningful. Hopefully in the future, these issues will be more fully considered when analyzing inhomogeneously broadened NC luminescence lifetimes, rather than defaulting to the simple stretched exponential model (Eq. 9) to describe and characterize the dynamical processes at work in the PL spectrum.
Methods
The SiNCs were synthesized according to a recently-proposed method [21]. Briefly, 4 g of hydrogen silsesquioxane (HSQ) was annealed at 1100 or 1200 °C for 1 h in a flowing 5% H2 + 95% Ar atmosphere, resulting in composites of SiNCs embedded in a silica matrix. These composites were mechanically ground into a fine powder using an agate mortar. The powder was shaken for about 8 h with glass beads using a wrist action shaker. The powders were suspended in 95% ethanol and interfaced to a vacuum filtration system equipped with a filter. To liberate the H-SiNCs, the silica matrix was removed via HF etching. An approximately 200 mg aliquot of the composite was transferred to a Teflon beaker to which 2 mL of ethanol, 2 mL of water, and 2 mL of 49% HF aqueous solution were added in order to dissolve the silica matrix. After stirring the suspension for 40 min, the liberated H-SiNCs were extracted as a cloudy yellow suspension using toluene and isolated by centrifugation at 3000 rpm for 5 min. The resulting hydrogen-terminated SiNCs were suspended in 10 mL dry toluene, and then transferred to an oven-dried Schlenk flask equipped with a magnetic stir bar. Subsequently, 1 mL of 1-dodecene (ca. 4.6 mmol), as well as 20 mg of AIBN were added. The suspension was subjected to three freeze-pump-thaw cycles using an Ar charged Schlenk line. After warming the suspension to room temperature, it was stirred for 24 h at 70 °C, and 10 mL of methanol and 20 mL of ethanol were subsequently added to the transparent reaction mixture. The resulting cloudy suspension was transferred to a 50 mL PTFE vial and the SiNCs were isolated by centrifugation at 12,000 rpm for 20 min. The SiNCs were re-dispersed in 10 mL toluene and isolated by addition of 30 mL ethanol antisolvent followed by another centrifugation. The latter procedure was carried out one more time. Finally, the dodecyl-SiNCs were re-dispersed in 5 mL dry toluene and stored in a screw capped vial (concentration ~ 0.5 mg/mL) for optical studies.
TEM samples were prepared by depositing the freestanding nanoparticles directly onto an ultrathin (ca. 3 nm) carbon-coated copper TEM grid. The NCs were imaged by bright-field TEM using a JEOL JEM-2010 and HRTEM was done on a JEOL JEM-ARM200CF. Fourier transform infrared spectroscopy (FTIR) was performed in a Nicolet 8700 from Thermo Scientific. X-ray photo-electron spectroscopy was measured in a SPECS system equipped with a Phoibos 150 2D CCD hemispherical analyzer and a Focus 500 monochromator. The detector angle was set perpendicular to the surface and the X-ray source was the Mg Kα line.
Luminescence spectra were excited with a 352-nm Ar + ion laser, which was pulsed (50% duty cycle, 50–250 Hz) using an Isomet IMDD-T110 L-1.5 acousto-optic modulator (AOM) with a fall time of ~ 50 ns. The used setup is schematically depicted in Fig. 7. The laser beam passes the acousto-optic modulator and one of the diffracted beams is selected by an iris. A beamsplitter reflects the main part of the pulsed laser beam into the sample cuvette and the incident power on the sample was ~ 8 mW spread over an area of ~ 4 mm 2 . The luminescence was collected with an optical fiber (numerical aperture 0.22), sent through a 450-nm longpass filter and is guided to the appropriate detector. The PL spectrum was measured by an Ocean Optics miniature spectrometer whose response function was corrected using a calibrated radiation source (the HL-3 + -CAL from Ocean Optics). The quantum efficiency was measured using an integrating sphere with 405-nm excitation, using a solution diluted to have an absorbance of ~ 0.15 at that wavelength.
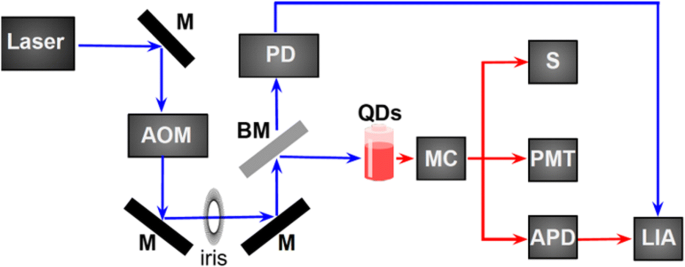
Diagram of the experimental setup. M mirror, AOM acousto-optic modulator, BM beamsplitter, PD photodiode, MC monochromator, S spectrometer, PMT photomultiplier tube, APD avalanche photodiode, LIA lock-in amplifier
The luminescence dynamics were measured with two different detectors. The first detector was the Thorlabs 120A2 avalanche photodiode (50 MHz roll-off), which was interfaced to a Moku:Lab (200 MHz) in digital oscilloscope mode. The second detector was a Hamamatsu h7422-50 photomultiplier tube interfaced to a Becker-Hickl PMS400 multiscalar. The error in the luminescence decay times was obtained by repeating the measurements three times, yielding a standard error in the mean lifetime calculated using the stretched exponential fit (Eq. 4) of 1 μs. All fits to the decay data were done in Origin using the least linear squares with the Levenberg-Marquardt algorithm, and were repeated in Matlab using the same method. For wavelength-dependent decay measurements, the luminescence was sent through an Acton MS2500i monochromator prior to detection, with the half width of the detected radiation set to ~ 3 nm.
For QFRS measurements, the AOM was set to produce a sinusoidal oscillation. A part of the incident beam was deflected into a Thorlabs PDA10A photodiode (200 MHz) in order to generate the reference signal. The SiNC PL response was simultaneously collected and sent to the APD. The reference signal was obtained using the beamsplitter, and along with the corresponding PL signal, was analyzed using the Moku:Lab in the lock-in amplifier mode to measure the in-phase and quadrature components of the signal.
Finally, we also searched for a short-lifetime component in the luminescence, as has sometimes been reported previously and attributed to oxidation [22]. This system used a 405-nm picosecond diode laser (Alphalas GmbH) to excite the NCs, and a Becker-Hickl HPM-100-50 PMT interfaced to an SPC-130 pulse counter system. This setup has a response time of ~ 100 ps. No evidence of a nanosecond decay was observed in these SiNCs.
Afkortingen
- APD:
-
Avalanche photodiode
- AQY:
-
Absolute quantum yield
- FRS:
-
Frequency-resolved spectroscopy
- LN:
-
Lognormal
- NCs:
-
Nanocrystals
- PL:
-
Fotoluminescentie
- PMT:
-
Photomultiplier tube
- QFRS:
-
Quadrature frequency-resolved spectroscopy
- SE:
-
Stretched exponential
- SiNCs:
-
Silicon nanocrystals
- TRS:
-
Time-resolved spectroscopy
Nanomaterialen
- Wat je hebt gemist op de Silicon Valley Connext Conference
- Helden in Silicon Valley (en op de RTI User's Group Meeting)
- Wat zijn de belangrijke toepassingen van siliciumcarbide?
- Silicium
- Silicon Labs:nieuw draadloos platform stelt next-gen verbonden producten in staat om het IoT te schalen
- In harmonie met het hart van een koperatoom
- Nanosilicium om waterstof te produceren
- Kan Taiwan de Silicon Valley of Agriculture 4.0 worden?
- Glijdende snelheidsafhankelijke tribochemische slijtage van oxidevrij silicium
- Ontrafeling van de morfologische evolutie en etskinetiek van poreuze silicium nanodraden tijdens metaalondersteunde chemische etsing
- De meest voorkomende toepassingen voor silicium-ijzerbrons



