Spin- en vallei-afhankelijke elektronische structuur in Siliceen onder periodieke potenties

Abstract

We bestuderen de spin- en vallei-afhankelijke energieband en transporteigenschap van siliceen onder een periodieke potentiaal, waarbij zowel spin- als valleidegeneraties worden opgeheven. Het is gebleken dat het Dirac-punt, de miniband, de bandafstand, de anisotrope snelheid en de conductantie sterk afhankelijk zijn van de spin- en dalindices. De extra Dirac-punten verschijnen naarmate de spanningspotentiaal toeneemt, waarvan de kritische waarden verschillend zijn voor elektronen met verschillende spins en valleien. Interessant is dat de snelheid sterk wordt onderdrukt vanwege het elektrische veld en het uitwisselingsveld, behalve het gapless grafeen. Het is mogelijk om een uitstekend collimatie-effect te bereiken voor een specifieke spin in de buurt van een specifieke vallei. De spin- en dal-afhankelijke bandstructuur kan worden gebruikt om het transport aan te passen, en perfecte transmissies worden waargenomen op Dirac-punten. Daarom wordt een opmerkelijke spin- en dalpolarisatie bereikt die effectief kan worden geschakeld door de structurele parameters. Belangrijk is dat de polarisaties van spin en vallei enorm worden versterkt door de wanorde van het periodieke potentieel.

Achtergrond

Tweedimensionale (2D) Dirac-materialen met hexagonale roosterstructuren worden uitgebreid onderzocht sinds de ontdekking van grafeen, zoals siliceen [1, 2], overgangsmetaaldichalcogeniden [3, 4] en fosforeen [5]. Hoewel grafeen veel specifieke eigenschappen heeft, wordt de toepassing ervan beperkt door de nulbandafstand en de zwakke spin-orbit-interactie (SOI). Onlangs is een siliciumanaloog van grafeen, siliceen, gefabriceerd via epitaxiale groei [6-10], en de stabiliteit ervan is voorspeld door theoretische studies [11, 12]. Grafeen en siliceen hebben vergelijkbare bandstructuren rond K en K ^′ valleien, en de lage-energiespectra van beide worden beschreven door de relativistische Dirac-vergelijking [13]. In tegenstelling tot grafeen heeft siliceen een sterke intrinsieke SOI en een kromme structuur. De sterke SOI zou een opening kunnen openen op Dirac-punten [13, 14] en leiden tot een koppeling tussen de vrijheidsgraden spin en dal. De geknikte structuur stelt ons in staat om de bandafstand te regelen door een extern elektrisch veld loodrecht op het siliceenvel [14–16]. Bovendien heeft siliceen het voordeel dat het beter compatibel is met de bestaande elektronische technologie op basis van silicium. Deze eigenschappen maken siliceen tot een uitstekend materiaal voor de volgende generatie nano-elektronica. In het bijzonder is een siliceen-veldeffecttransistor bij kamertemperatuur met succes gefabriceerd door een groei-overdracht-fabricageproces in experiment [17].

De ontdekking van 2D Dirac-materialen biedt nieuwe mogelijkheden om de kwantumcontrole van de vallei te verkennen. De twee ongelijke valleien K en K ^′ in de eerste Brillouin-zone kan worden beschouwd als een extra vrijheidsgraad naast lading en spin voor kwantuminformatie en kwantumberekening [18-20]. De vrijheidsgraad van het dal kan bijvoorbeeld worden ingebouwd om een elektron-spin-qubit uit te breiden tot een spin-vallei-qubit [18]. Daarom heeft valleytronics, dat tot doel heeft de vallei-pseudo-spin te genereren, te detecteren en te manipuleren, veel belangstelling gewekt. In grafeen zijn verschillende schema's voorgesteld om een dalpolarisatie te bereiken door gebruik te maken van unieke randmodi [21, 22], trigonaal kromtrekkend effect [23], topologische lijndefecten [24, 25], spanning [26, 27] en elektrostatische poorten [28]. In vergelijking met grafeen heeft siliceen een aanzienlijk voordeel bij de studie van pseudospin uit de vallei. Het is gebleken dat siliceen een rijke verscheidenheid aan topologische fasen en Chern-getallen vertoont onder de modulatie van verschillende externe velden [13, 16, 29, 30]. In aanwezigheid van elektrisch veld E _z en wissel veld h uit , Ezawa verkende het fasediagram in de E _z −h vlak dat wordt gekenmerkt door de spin- en dalindices [16]. Verder rekening houdend met de Rashba SOI, wordt een vallei-gepolariseerde kwantum afwijkende Hall-toestand voorspeld in siliceen vanwege de topologische faseovergang [31]. Op basis van de toestandsovergang wordt een op siliceen gebaseerd spinfilter met bijna 100% spinpolarisatie voorgesteld dat robuust is tegen zwakke wanorde [32]. Yokoyama bestudeerde het ballistische transport door een ferromagnetische (FM) siliceenovergang en toonde een controleerbare spin- en dal-gepolariseerde stroom [33]. In overgangsmetaaldichalcogeniden met een gebroken inversiesymmetrie, is de spinsplitsing van de valentiebanden die voortkomen uit intrinsieke SOI tegengesteld aan de twee valleien vanwege een tijdomkeersymmetrie [3, 34, 35]. De verbroken inversiesymmetrie zou kunnen resulteren in een vallei-afhankelijke optische selectieregel, die kan worden gebruikt om dragers selectief te exciteren in de K of K ^′ vallei via respectievelijk rechts of links circulair gepolariseerd licht [3, 34]. In experiment is het signaal van valleipolarisatie onderzocht door optische [36, 37] en transport [38, 39] metingen. Een gigantisch niet-lokaal Hall-effect in de vallei werd waargenomen in dubbellaags grafeen dat werd onderworpen aan een symmetrie-brekend elektrisch poortveld, en het niet-lokale signaal houdt aan tot kamertemperatuur [38]. Een recent overzicht van valleytronics in 2D Dirac-materialen is te vinden in Ref. [40].

Superrooster is een effectieve methode om de elektronische structuur in halfgeleiders en 2D-materialen te construeren [41]. Superroosterpatronen met nanoschaal kunnen natuurlijk ontstaan in experimenten wanneer grafeen of siliceen op metalen substraten wordt geplaatst [42, 43]. Een superrooster in grafeen zou kunnen leiden tot renormalisatie van de anisotrope Fermi-snelheid [44] en het genereren van nieuwe Dirac-punten in het spectrum [45-47] vanwege de chirale aard, die experimenteel zijn waargenomen [43, 48, 49]. In siliceen superroosters met elektrisch veld E _z en wissel veld h uit , worden zowel spin- als daldegeneraties opgeheven. Het is bevestigd dat de minibandstructuur en minigaps veroorzaakt door de superroosters afhankelijk zijn van de spin- en valley-indices [50]. Bovendien zouden de spin- en valleipolarisaties kunnen worden verbeterd door de superroosters van siliceen [51]. Net als grafeen worden veel nieuwe elektronische structuren verwacht in superroosters van siliceen. Er zijn echter zeer weinig werken aan superroosters van siliceen [50, 51]. In dit artikel bespreken we in detail een complementair aspect, namelijk de spin- en vallei-afhankelijke bandstructuur en transporteigenschap van siliceen. We ontdekten dat de spin- en vallei-indices verschillende effecten hebben op de extra Dirac-punten en anisotrope snelheid die kunnen worden afgestemd door de structurele parameters. De snelheid wordt sterk onderdrukt door het elektrische veld en het uitwisselingsveld. Er wordt een opmerkelijke spin- en valleipolarisatie bereikt, die sterk kan worden versterkt door de stoornis.

Het blad is als volgt ingedeeld. In de sectie “Methoden” presenteren we het theoretische formalisme en de dispersierelatie. De numerieke resultaten op bandstructuur, spin en dal gepolariseerde transmissies worden getoond in de sectie "Resultaten en discussies". Ten slotte sluiten we af met een samenvatting in de sectie "Conclusies".

Methoden

In de benadering van één deeltje gehoorzaamt de elektronische structuur van siliceen in de buurt van Dirac-punten aan een effectieve Dirac Hamiltoniaan. Het systeem in kwestie is een eendimensionaal superrooster van siliceen gevormd door een reeks lokale potentiële barrières U , wissel velden uit h , en loodrecht elektrisch veld E _z . U , h , en E _z zijn alleen aanwezig in de barrièregebieden met barrièrebreedte d _b , terwijl U =h =E _z =0 in de putgebieden met putbreedte d _w , zoals weergegeven in Fig. 1. Het superrooster met een Kronig-Penney-type varieert alleen langs x richting, en de lengte van één eenheid is d =d _b +d _w . Een soortgelijk model is besproken in Refs. [51, 52], die zich voornamelijk richten op thermo-elektrisch en elektronisch transport in plaats van de bandstructuur en het wanorde-effect dat in dit werk wordt bestudeerd. Experimenteel, U kan worden geproduceerd door de metalen poorten en h kan worden geproduceerd door het magnetische nabijheidseffect met FM-isolatoren EuO [33], die periodiek bovenop de siliceenlaag worden afgezet (zie figuur 1). Het elektrische veld E _z toegepast loodrecht op siliceen kan een verspringend subroosterpotentieel induceren Δ _z =ℓ E _z , met 2ℓ ≈0.46Å de verticale scheiding van A en B plaatsen van de twee subroosters vanwege de geknikte structuur [16]. Daarom kunnen de elektronische toestanden worden beschreven door de Hamiltoniaan,

$$\begin{array}{@{}rcl@{}} H =\hbar v_{F} (k_{x} \tau_{x} - \eta k_{y} \tau_{y}) + \Delta_ {\eta \sigma} \tau_{z} + U_{\sigma}. \end{array} $$ (1)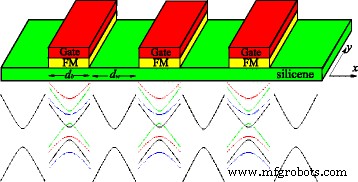

Boven:schema van de superroosters van siliceen. De FM-isolatoren, zoals EuO en EuS, bovenop siliceen induceren de uitwisselingsvelden in siliceen, zoals voorgesteld voor grafeen [53]. De metalen poorten aan de bovenkant van FM-isolatoren regelen het Fermi-niveau lokaal. Onder:schema van het energiespectrum in siliceen met en zonder externe velden

Δ _{η σ} =Δ _z −η σ λ _ZO beschrijft de band gap voor verschillende spin- en valley-indices, die kan worden gecontroleerd door het gespreide potentieel Δ _z en de SOI λ _ZO . U _σ =U −σ h is het effectieve potentieel voor verschillende spin-indices. η =±1 geeft de K . aan en K ^′ valleien. σ =±1 geeft spin-up en spin-down toestanden aan. v _F is de Fermi-snelheid. In siliceen zijn de intrinsieke en extrinsieke Rashba-effecten erg klein en kunnen ze worden verwaarloosd [15].

Vanwege de translationele invariantie langs de y richting, de transversale golfvector k _j wordt geconserveerd. De golffunctie voor vallei η en draai σ in elke regio heeft de vorm Ψ (x ,j )=ψ (x )e ^iky _j met

$$\begin{array}{@{}rcl@{}} \psi(x) =A \left(\begin{array}{cc} 1 \\ \frac{\hbar v_{F} k_{-} }{\epsilon_{\eta \sigma}} \end{array}\right) e^{i q_{\eta \sigma} x} + B \left(\begin{array}{cc} 1 \\ \frac {- \hbar v_{F} k_{+}}{\epsilon_{\eta \sigma}} \end{array}\right) e^{-i q_{\eta \sigma} x}. \end{array} $$ (2)

In de barrièregebieden, ε _{η σ} =ε _b =(E −U _σ )+Δ _{η σ} en de x component van de golfvector $ q_{\eta \sigma } =q_{b} =\sqrt {(E - U_{\sigma })^{2} - \Delta ^{2}_{\eta \sigma } - (\hbar v_{F} k_{y})^{2}} / \hbar v_{F} $. In de brongebieden, ε _{η σ} =ε _w =E −η σ λ _ZO en $ q_{\eta \sigma } =q_{w} =\sqrt {E^{2} - \lambda _{SO}^{2} - (\hbar v_{F} k_{y})^{ 2}} / \hbar v_{F} $. k _± =q _{η σ} ±ik η k _j . De transmissiekans T _{η σ} kan worden berekend met behulp van de transfermatrixtechniek. De genormaliseerde conductantie voor een bepaalde spin in een bepaalde vallei bij nultemperatuur wordt gegeven door

$$\begin{array}{@{}rcl@{}} G_{\eta \sigma} (E) =\frac{1}{2} \int_{-\pi/2}^{\pi/2 } T_{\eta \sigma} (E,E\sin \theta) \cos \theta d \theta, \end{array} $$ (3)

waar θ is de invalshoek ten opzichte van de x richting. De spin- en dal-opgeloste conductanties worden gedefinieerd als $G_{\uparrow (\downarrow)} =\left (G_{K \uparrow (\downarrow)} + G_{K^{\prime } \uparrow (\downarrow) )} \right) / 2 $ en $G_{K (K^{\prime })} =\left (G_{K (K^{\prime }) \uparrow } + G_{K (K^{ \prime }) \downarrow } \right) / 2$, respectievelijk. Vervolgens introduceren we de spinpolarisatie P _s en vallei polarisatie P _v :

$$\begin{array}{@{}rcl@{}} P_{s} =(G_{\uparrow} - G_{\downarrow}) / (G_{\uparrow} + G_{\downarrow}), \ end{array} $$ (4) $$\begin{array}{@{}rcl@{}} P_{v} =(G_{K} - G_{K^{\prime}}) / (G_{ K} + G_{K^{\prime}}). \end{array} $$ (5)

Gebaseerd op de stelling van Bloch en de continuïteitsvoorwaarde van golffuncties, is de dispersierelatie E (k _x ) voor spin-up en spin-down elektronen nabij de K en K ^′ dalen kunnen worden berekend,

$$ \begin{uitgelijnd} \cos(k_{x} d) &=\cos(q_{w} d_{w}) \cos(q_{b} d_{b}) \\&\quad- \frac {(\epsilon_{b} q_{w})^{2} + (\epsilon_{w} q_{b})^{2} + (\epsilon_{b} \!- \!\epsilon_{w}) ^{2} k^{2}_{y}}{2 \epsilon_{w} \epsilon_{b} q_{w} q_{b}} \sin(q_{w} d_{w}) \sin( q_{b} d_{b}), \end{uitgelijnd} $$ (6)

en k _x is het Bloch-golfnummer. Om de berekening te vereenvoudigen worden de dimensieloze eenheden geïntroduceerd:$E \rightarrow E d / \hbar v_{F}$, $U \rightarrow U d / \hbar v_{F}$, $\ lambda _{SO} \rightarrow \lambda _{SO} d / \hbar v_{F}$, $\Delta _{z} \rightarrow \Delta _{z} d / \hbar v_{F}$ , $h \rightarrow hd / \hbar v_{F}$, k _j →k _j d , k _x →k _x d , d _w →d _w /d , en d _b →d _b /d . Merk op dat bij Δ _z =λ _ZO =h =0, vgl. (6) wordt gereduceerd tot degene die wordt gevonden voor gapless grafeen in een periodieke potentiaal, waar zowel spin als vallei gedegenereerd zijn [44-47]. Van verg. (6), we kunnen dat uitwisselingsveld h . zien alleen zou de splitsing van spin kunnen veroorzaken, terwijl de vallei degenereert. De degeneratie van de vallei kan echter worden opgeheven door het elektrische veld E _z met de hulp van de SOI λ _ZO . Dus een combinatie van het uitwisselingsveld en het elektrische veld zou de spin- en daldegeneraties [16, 31-33] kunnen opheffen, zoals weergegeven in figuur 1. In het voorgestelde systeem zouden elektronen met verschillende spins in de buurt van verschillende valleien verschillende banden vertonen constructies en transportfuncties.

Resultaten en discussies

In deze sectie zouden we de bovenstaande vergelijkingen gebruiken om de bandstructuren en transporteigenschappen voor verschillende spin- en vallei-indices in siliceen-superroosters te berekenen. In wat volgt wordt aangenomen dat de breedtes van barrières en putten hetzelfde zijn. De resultaten voor de casus met ongelijke put- en barrièrebreedtes (d _b d _w ) zijn vergelijkbaar met die in gapless grafeen [47]. Sommige parameters zijn ingesteld als d _b =d _w =50 nm en λ _ZO =3,9 meV in siliceen, tenzij anders vermeld. We zullen ons concentreren op de eerste twee minibanden (de laagste valentie- en geleidingsminibanden) nabij het Fermi-niveau.

Spin- en vallei-afhankelijke bandstructuur

Ten eerste, het effect van potentiële U op minibanden is afgebeeld in Fig. 2. Om het geval met gapped en gapless van energiebanden tegelijkertijd te bespreken, stellen we Δ _z =7,8 meV=2λ _ZO . Bij afwezigheid van potentieel (U =0), het spin-up elektron nabij K vallei (K ↑ elektron) en spin-down elektron nabij K ^′ vallei (K ^′ ↓ elektron) zijn gapless (zie Fig. 2 (a1, a4)), terwijl het spin-down elektron nabij K vallei (K ↓ elektron) en spin-up elektron nabij K ^′ vallei (K ^′ ↑ elektron) hebben een grote opening (zie figuur 2 (a2, a3)). De minibanden van spin-up (of spin-down) elektron verschuiven naar het negatieve (of positieve) energiebereik van E =0 door h , vanwege het effectieve potentieel U _σ =U −σ h . De bandstructuren van K ↑ (of K ↓ ) elektron en K ^′ ↓ (of K ^′ ↑ ) elektronen presenteren spiegelsymmetrie met betrekking tot E =0, consistent met Vgl. (6). Deze spiegelsymmetrie wordt echter vernietigd in aanwezigheid van U . Opmerkelijk, zoals U stijgt, verschijnen er extra Dirac-punten, waarvan het aantal ondertussen toeneemt. De extra Dirac-punten kunnen worden aangetoond door de chiraliteit van de golffuncties in hun nabijheid [46]. De kenmerken van Dirac-punten in het siliceensysteem zijn sterk afhankelijk van de vrijheidsgraden spin en dal, zoals weergegeven in figuur 2. Bijvoorbeeld bij U =135 meV in Afb. 2 (d1-d4) voor K ↑ , K ↓ , K ^′ ↑ en K ^′ ↓ elektronen, het aantal Dirac-punten is respectievelijk 5, 6, 4 en 7. Voor specifieke waarden van U , zoals U =40,66 meV voor K ↓ elektron (zie Fig. 2 (b2)) en U =100,63 meV voor K ^′ ↑ elektron (zie Fig. 2 (c3)), kan een nieuw Dirac-punt worden gegenereerd op k _j =0, en het zal zich splitsen in een paar dat in tegengestelde richting beweegt, weg van de k _j =0 punt maar altijd k . behouden _x =0, als U verder toeneemt. Als gevolg hiervan zijn de bandhiaten voor K ↓ en K ^′ ↑ elektronen zijn gesloten (zie figuur 2 (b2, c3)), en het systeem met gaten wordt gapless. Om de kritieke waarde van U . te vinden , we stellen d . in _b =d _w en k _x =0. Analoog aan de regel in gapless grafeen [47], rekening houdend met de impliciete functiestelling, kan men concluderen dat de longitudinale golfvectoren op de nieuwe Dirac-punten voldoen aan q _b =q _w wanneer

$$\begin{array}{@{}rcl@{}} E_{0} =\frac{(U - \sigma h)^{2} - \Delta_{z}^{2} + 2 \eta \ sigma \Delta_{z} \lambda_{SO}}{2(U - \sigma h)}. \end{array} $$ (7)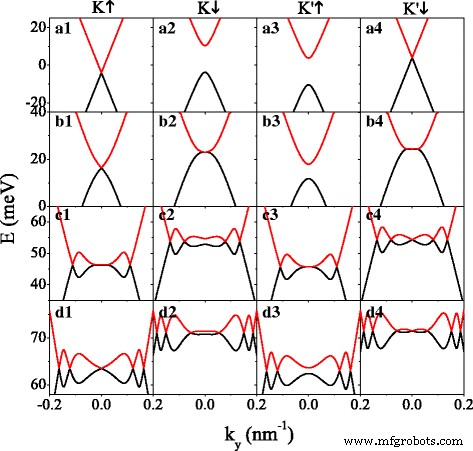

Energiespectrum versus k _j voor verschillende waarden van potentiële U . (a1–a4) U =0; (b1-b4) U =40,66 meV; (c1-c4) U =100,63 meV; (d1-d4) U =135,0 meV. De waarden van parameters zijn h =8,0 meV, Δ _z =7,8 meV, en k _x =0

Voor K ↑ en K ^′ ↓ elektronen met η σ =1, wanneer Δ _z =2λ _ZO , Verg. (7) kan verminderen tot

$$\begin{array}{@{}rcl@{}} E_{0} =\frac{U - \sigma h}{2}. \end{array} $$ (8)

Dienovereenkomstig, Vgl. (6) verandert in

$$ {}\cos^{2}(q_{w} d_{w}) - \frac{\left(\epsilon_{b}^{2} + \epsilon_{w}^{2}\right) q_ {w}^{2} + (\epsilon_{b} - \epsilon_{w})^{2} k^{2}_{y}}{2 \epsilon_{w} \epsilon_{b} q_{w }^{2}} \sin^{2}(q_{w} d_{w}) =1, $$ (9)

waaraan is voldaan als $\left (\epsilon _{b}^{2} + \epsilon _{w}^{2}\right) q_{w}^{2} + (\epsilon _{b} - \epsilon _{w})^{2} k^{2}_{y} =-2 \epsilon _{w} \epsilon _{b} q_{w}^{2}$ of q _w d =2n π (n is een positief geheel getal). Gebaseerd op vgl. (8), we hebben ε _b =−ε _w , en dus is de vorige gelijkheid alleen vervuld als k _{j 0} =0 voor K ↑ en K ^′ ↓ elektronen bij Δ _z =2λ _ZO , overeenkomend met het oorspronkelijke Dirac-punt. De oplossingen van q _w d =2n π heb het formulier

$$\begin{array}{@{}rcl@{}} k_{y0} =\pm \frac{1}{d} \sqrt{\frac{\left(E_{0}^{2}-\ lambda_{SO}^{2}\right)d^{2}}{(\hbar v_{F})^{2}} - (2n\pi)^{2}}. \end{array} $$ (10)

Wanneer $\sqrt {E_{0}^{2}-\lambda _{SO}^{2}}d / 2\pi \hbar v_{F} \geq n$, k _{j 0} echt is, en de nieuwe Dirac-punten zullen verschijnen die zich precies op (E . bevinden) ₀ ,k _{j 0} ). Bij lage waarden van U , k _{j 0} is denkbeeldig, en er is geen oplossing voor n , wat geen extra Dirac-punten betekent. De Dirac-punten verschijnen pas na een kritische waarde van U , zoals U =40,66 meV voor K ↓ elektronen in Fig. 2 (b2), overeenkomend met n =1. Volgens vgl. (10), Het aantal Dirac-punten N _D kan worden verkregen. Wanneer Δ _z =2λ _ZO ,

$$\begin{array}{@{}rcl@{}} N_{D} =2 \left[ \frac{\sqrt{E_{0}^{2}-\lambda_{SO}^{2}} d}{2\pi\hbar v_{F}} \right] + 1 \end{array} $$ (11)

voor K ↑ en K ^′ ↓ elektronen, terwijl

$$\begin{array}{@{}rcl@{}} N_{D} =2 \left[ \frac{\sqrt{E_{0}^{2}-\lambda_{SO}^{2}} d}{2\pi\hbar v_{F}} \right] \end{array} $$ (12)

voor K ↓ en K ^′ ↑ elektronen, waarbij [...] staat voor een geheel getal. Merk op dat bij de kritische waarde van U , zoals U =40,66 meV en 100,63 meV, het aantal Dirac-punten is N _D =2n −1 voor K ↓ en K ^′ ↑ elektronen (zie Fig. 2 (b2, c3)).

Uit vergelijkingen (7) en (10) blijkt dat de posities en het aantal Dirac-punten kunnen worden aangepast door het elektrische veld E _z en wissel veld h uit . Afbeelding 3 toont het aantal Dirac-punten N _D als een functie van U voor verschillende waarden van E _z en h . Wanneer Δ _z =7,8 meV in Fig. 3a, met toenemende U , N _D voor K ↑ en K ^′ ↓ elektronen neemt toe in de vorm van een oneven getal, in overeenstemming met Vgl. (11). N _D voor K ↓ en K ^′ ↑ elektronen neemt toe in de vorm van een even getal, in overeenstemming met Vgl. (12), behalve N _D op de kritische waarde. Vergelijking tussen Fig. 3a en b geeft aan dat als h toeneemt, neemt de kritische waarde voor spin-down (of spin-up) elektron geleidelijk af (of neemt toe). Wanneer Δ _z =15 meV≠2λ _ZO in Afb. 3c, N _D voor alle elektronen neemt toe in de vorm van een even getal, behalve voor N _D op de kritische waarde. Duidelijk, de kritische waarden van U zijn verschillend voor elektronen met verschillende spins en valleien. De Dirac-punten kunnen worden gecontroleerd door een gezamenlijke modulatie van de parameters U , E _z , en h .

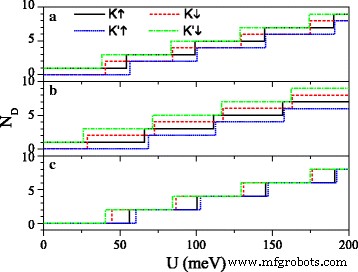
Aantal Dirac-punten N _D versus potentiële U . (een ) h =8,0 meV en Δ _z =7,8 meV; (b ) h =20,0 meV en Δ _z =7,8 meV; (c ) h =8,0 meV en Δ _z =15,0 meV

De potentiële U en barrièrebreedte d _b kan worden gebruikt om de band gap te regelen, zoals geïllustreerd in Fig. 4. De hiaten voor K ↑ en K ^′ ↓ elektronen zijn klein, terwijl de hiaten voor K ↓ en K ^′ ↑ elektronen zijn groot vanwege Δ _{η σ} =Δ _z −η σ λ _ZO . Als U neemt toe, bewegen alle minibanden geleidelijk naar een gebied met hoge energie (zie figuur 4a), en alle bandhiaten vertonen gedempte oscillatie met U (zie afb. 4b). Wanneer U =σ h , het effectieve potentieel is nul en de kloof bereikt de maximale waarde. De kloof is gesloten bij de kritische waarde van U , vanwege de opkomst van nieuwe Dirac-punten. Afbeelding 4c, d geeft de afhankelijkheid weer van minibands en bandgaps van de barrièrebreedte d _b bij U =0. Bij afwezigheid van een extern veld (d _b =0), de minibanden blijven degenereren en de kloof op Fermi-niveau is 2λ _ZO . Met het uiterlijk van d _b , wordt de miniband gesplitst, waar vallei en spin niet-ontaard worden. De minibands van K ↑ (of K ↓ ) en K ^′ ↓ (of K ^′ ↑ ) elektronen behouden spiegelsymmetrie rond E =0 (zie Fig. 4c). Als d _b neemt toe, de hiaten van K ↓ en K ^′ ↑ elektronen worden geleidelijk breder. De hiaten van K ↑ en K ^′ ↓ elektronen nemen af tot nul wanneer d _b voldoet aan d _b /d _w =λ _ZO /Δ _z , en daarna verhogen met d _b (zie afb. 4d). De spleetbreedten naderen verzadiging met de verdere toename van d _b . Verder is de breedte van de miniband versmald als d _b neemt toe (niet weergegeven in de figuur), vanwege de minder koppeling van eigentoestanden. Het effect van elektrisch veld op bandgap is analoog aan dat in eerdere studie [50].

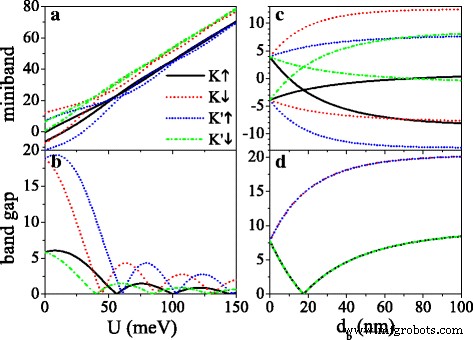
(een ) Minibands in de buurt van Fermi-niveau en (b ) hun bandhiaten op het oorspronkelijke Dirac-punt versus potentiële U , bij d _b =d _w =50nm. (c ) Minibands in de buurt van Fermi-niveau en (d ) hun band gaps op het originele Dirac-punt versus d _b , bij U =0 en d _w =50nm. De waarden van andere parameters zijn h =8,0 meV, Δ _z =15,0 meV, en k _x =k _j =0

De groepssnelheid is sterk afhankelijk van de spin- en valley-indices, zoals weergegeven in Fig. 5. De componenten (v _x ,v _j ) van snelheid kan worden gedefinieerd als

$$\begin{array}{@{}rcl@{}} v_{x} / v_{F} =\partial E / \partial k_{x}, \quad v_{y} / v_{F} =\ gedeeltelijk E / \gedeeltelijk k_{y}. \end{array} $$ (13)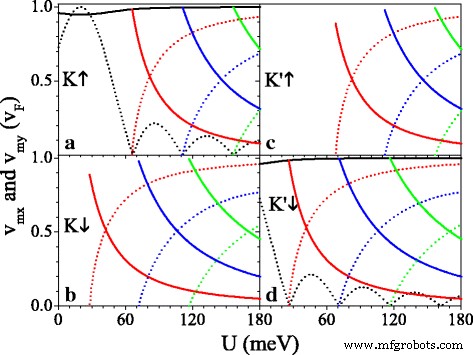

(een –d ) Snelheid versus potentiële U , en de parameters zijn ingesteld als h =20,0 meV en Δ _z =7,8 meV. De zwarte, rode, blauwe en groene effen curven zijn de snelheden v _0x , v _1x , v _2x , en v _3x , respectievelijk. De zwarte, rode, blauwe en groene stippellijnen zijn de snelheden v _0j , v _1j , v _2j , en v _3j , respectievelijk

Afbeelding 5 toont de snelheidscomponenten v _mx en v _mijn in eenheden van v _F op het oorspronkelijke Dirac-punt (m =0) en nieuwe Dirac-punten (m =1,2,3). Je kunt dat zien als U neemt toe, v _0j oscilleert op een vervallen manier en v _0x ≈v _F is bijna onaangetast (zie Fig. 5a, d). Bij de kritische waarde van U waar de nieuwe Dirac-punten verschijnen, v _mx ≈v _F maar v _0j =v _mijn =0, wat wijst op een collimatiegedrag langs de k _x richting voor specifieke spins en valleien. Wanneer U overschrijdt de kritische waarde en neemt verder toe, v _mijn verhogen tot v _F maar v _mx geleidelijk tot nul afnemen. Het effect van de periodieke potentiaal is sterk anisotroop, als gevolg van het chirale karakter. De kenmerken van anisotrope snelheid zijn verschillend voor verschillende spins en valleien vanwege de kloof Δ _{η σ} en de potentiële U _σ , die kan worden aangestuurd door U . te gebruiken . U . nemen =20 meV bijvoorbeeld, v _0j =v _F voor K ↑ elektron is veel groter dan v _0j =0.16v _F voor K ^′ ↓ elektron, en geen v _0j voor K ↓ en K ^′ ↑ elektronen door de bandgap. v _mx (of v _mijn ) voor spin-up elektron is altijd groter (of kleiner) dan die voor spin-down elektron in dezelfde vallei. Met name impliceert figuur 5 ook dat voor een kleine waarde van U , v _0x , v _0j , en v _mx zijn kleiner dan v _F vanwege Δ _z en h , anders dan het gapless systeem [44]. Bijvoorbeeld v _1x =0.98v _F , 0,89v _F , 0,89v _F , en 0,98v _F voor K ↑ , K ↓ , K ^′ ↑ en K ^′ ↓ elektronen, wanneer het Dirac-punt verschijnt. Om de invloed van Δ . te verlichten _z en h op de groepssnelheid toont Fig. 6 de snelheden (v _0x ,v _0j ) als functie van (a) Δ _z en (b) h voor K ↑ elektron. Uit Fig. 6a kunnen we duidelijk zien dat v _0x neemt monotoon af met Δ _z terwijl v _0j is ongevoelig voor de verandering van Δ _z . Integendeel, v _0x is ongevoelig gemaakt voor h , terwijl v _0j neemt toe tot maximale waarde v _0j =v _F om u =σ U en neemt dan af met h . De resultaten geven aan dat de groepssnelheid kan worden onderdrukt door Δ _z en h in siliceen.

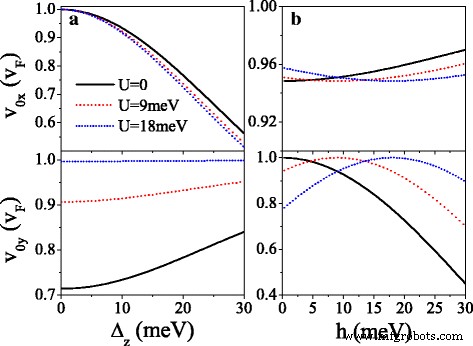
Snelheden v _0x en v _0j versus (een ) Δ _z en (b ) h , voor K ↑ elektron. (een ) h =20,0 meV en λ _ZO =Δ _z /2. (b ) Δ _z =7,8 meV

Spin- en Valley-gepolariseerd transport

De spin- en dalafhankelijke bandstructuur wordt weerspiegeld in de transporteigenschap en biedt een leidraad bij het regelen van het transport. In deze sectie bespreken we de eigenschappen van spin- en vallei-gepolariseerd transport door een eindig superrooster van siliceen. Afbeelding 7 toont de transmissiekans T _{η σ} voor (a, c) K ↑ en (b, d) K ↓ elektronen, en het periodenummer n =10. De rode gestippelde curven zijn de minibanden, die ook de grenzen zijn voor verschillende elektronische toestanden die de transmissie bepalen. We kunnen zien dat de transmissie beperkt is in het minibandgebied en geen transmissie in het bandgapgebied (zie figuur 7a, b). De distributie van transmissie is symmetrisch rond k _j =0 vanwege de symmetrische minibanden. De resonantiekarakteristiek van transmissie komt voort uit de resonantietoestanden. Opgemerkt moet worden dat de transmissie nog steeds bestaat in het hiaatgebied nabij k _j =0 vanwege het tunneleffect van eigentoestanden. T _{η σ} op Fermi-niveau voor K ↑ en K ↓ elektronen worden respectievelijk getoond in Fig. 7c, d). Je kunt duidelijk zien dat veel dunne resonantiepieken met T _{η σ} =1 komen precies voor op de posities van de Dirac-punten, wat een toepassing van het systeem als een spin- en dalfilter suggereert.

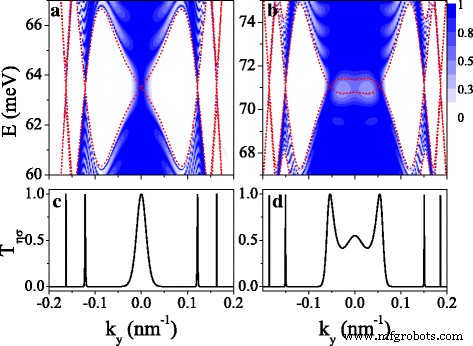
Contourplot van de transmissie T _{η σ} (E ,k _j ) voor (een ), (c ) K ↑ elektron en (b ), (d ) K ↓ elektron. De waarden van parameters zijn dezelfde als deze in Fig. 2 (d1-d4) en n =10

De sterke afhankelijkheid van de bandstructuur van de spin- en valley-indices is gunstig voor het realiseren van hoge spin- en valley-polarisaties. Afbeelding 8 toont de minibanden, conductanties G _{η σ} , spinpolarisatie P _s , en dalpolarisatie P _v als een functie van potentiële U . It can be found that the distribution of conductance is completely in agreement with the band structure, that is, the conductance (or conductance gap) corresponds to the miniband (or band gap). The minibands for spin-up and spin-down electrons could be alternative distribution by adjusting h properly. Consequently, $G_{K(K^{\prime })\uparrow }$ and $G_{K(K^{\prime })\downarrow }$ present alternative distribution as well, i.e., $G_{K(K^{\prime })\uparrow }$ nearly vanishes for those regions where $G_{K(K^{\prime })\downarrow }$ is in resonance and vice versa. This result directly leads to a remarkable spin polarization, proposing a switching effect of spin polarization (see Fig. 8a). By changing Δ _z , the minibands and conductances for electrons near K and K ^′ valleys could be controlled, leading to a fully valley-polarized current (see Fig. 8b). Compared with spin polarization, the valley polarization is not perfect enough. However, this drawback could be remedied via the disorder structure of the system, as discussed in the following.

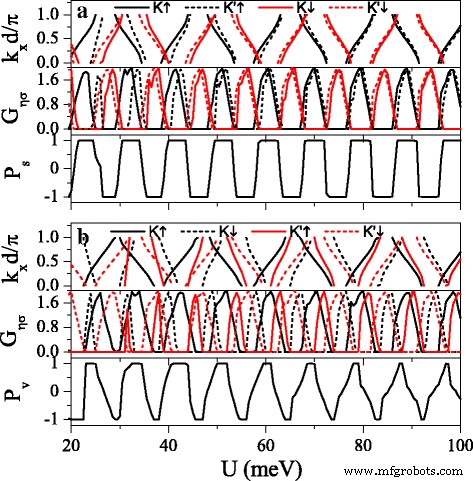
Minibands, conductances G _{η σ} , spin polarization P _s , and valley polarization P _v versus potential U . (een ) Δ _z =4.0 meV. (b ) Δ _z =12.0 meV. Other parameters are set as h =7.0 meV, E =6.0 meV, d _b =d _w =120 nm, and n =10

Figure 9 shows the (a) spin polarization P _s and (b) valley polarization P _v in (U ,h ) space. Interestingly, both P _s and P _v present periodical changes in the considered region, which is not observed in the ferromagnetic silicene junction [33]. Both distributions of P _s and P _v are antisymmetric with respect to h →−h . It is possible to achieve independently a full spin and valley polarization by a proper tuning of the fields U en h . For example, when h =6 meV and U =42 meV, P _s ≈1 and P _v ≈1, meaning that the current is mainly contributed by K ↑ electrons. When h =6 meV and U =44 meV, P _s ≈1 and P _v ≈−1 while P _s ≈−1 and P _v ≈−1 at h =6 meV and U =46 meV. The results demonstrate that a spin and valley polarization can be switched effectively.

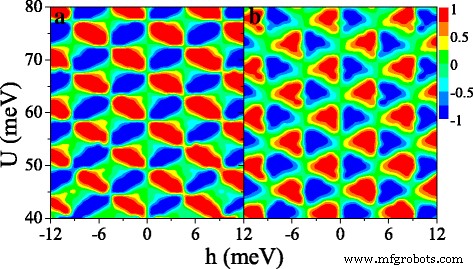
Contour plot of (a ) spin polarization P _s (U ,h ) en (b ) valley polarization P _v (U ,h ), at Δ _z =10.0 meV. The values of other parameters are the same as these in Fig. 8

In experiment, the structural imperfection of the model is unavoidable due to the limitations of the experimental techniques. Therefore, it is necessary to discuss the effect of the disorder on transmission. When the electric field or exchange field presents disorder, the conductance, spin polarization, and valley polarization are shown in Figs. 10 and 11. We set disorder situations of Δ _z en h fluctuate around their mean values, given by 〈Δ _z 〉=Δ _{z 0} and 〈h 〉=h ₀ , respectievelijk. The fluctuations are given by

$$\begin{array}{@{}rcl@{}} \Delta_{z} |_{i} =\Delta_{z0} (1 + \delta \zeta_{i}), \quad h |_{i} =h_{0} (1 + \delta \zeta_{i}), \end{array} $$ (14)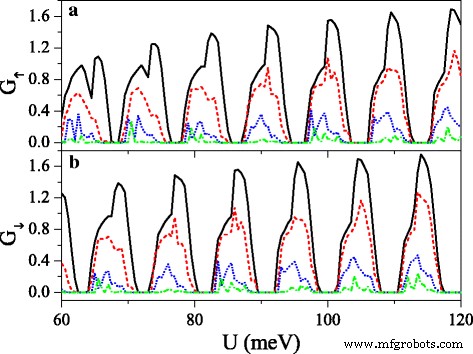

Conductances (a ) G _↑ and (b ) G _↓ versus potential U , when the electric field presents disorder, at n =50 and Δ _{z 0} =20.0 meV. The solid, dashed, dotted, and dash-dotted curves correspond to the disorder strength δ =0.0, 0.1, 0.3, and 0.6, respectively. The values of other parameters are the same as these in Fig. 8

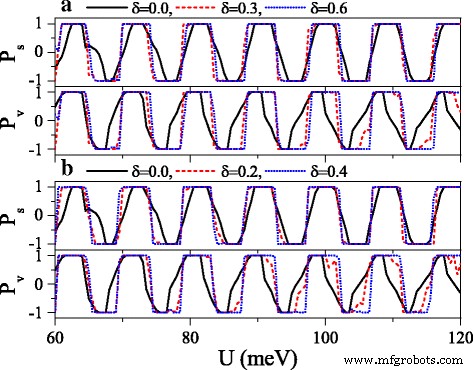
Polarizations P _s and P _v versus potential U when a the electric field or b the exchange field presents disorder. Δ _{z 0} =20.0 meV and h =7.0 meV in (a ). Δ _z =20.0 meV and h ₀ =7.0 meV in (b ). The values of other parameters are the same as these in Fig. 10

where {ζ _ik } is a set of uncorrelated random variables or white noise, − 1<ζ _ik <1, δ is the disorder strength, and i is the site index. Note that the disorder only takes place in the x direction, and the system is always homogeneous in y direction. Thus, k _j still keeps conservation. Figure 10 exhibits the effect of the disorder of the electric field on the conductances (a) G _↑ and (b) G _↓ . With the presence and increase of the disorder strength δ , both G _↑ and G _↓ are suppressed gradually, and each resonant peak splits into many small peaks. One may find that the conductance range is narrowed while the conductance gap range is broadened. Hence, the allowable (or forbidden) ranges of G _↑ completely fall into the forbidden (or allowable) ranges of G _↓ , giving rise to an excellent spin polarization (see Fig. 11). Furthermore, the positions of conductances and conductance gaps are nearly invariable as δ changes, suggesting that the miniband and band gap are insensitive to the disorder. Note that the disorder effect of the electric field on G _K and G _K ^′ is similar to that observed in Fig. 10. Figure 11 presents the disorder effects of (a) the electric field and (b) the exchange field on polarizations P _s and P _v . Obviously, with the increase of δ , P _s and P _v increase greatly, and the polarization platform is broadened. Thus, a full spin and valley polarization is realized. Comparison between Fig. 11a and b indicates that the disorder effect of exchange field is more prominent. The results demonstrate that the disorder could enhance the spin and valley polarizations compared with the order case, which is an advantage in realistic application.

Conclusies

In summary, we demonstrated detailedly that band structure and transport property of silicene under a periodic field strongly depend on the spin and valley degrees of freedom. The numerical results indicate that electrons with different spins and valleys have various characteristics in Dirac point, bang gap, and group velocity. In particular, owing to the electric field and exchange field, the anisotropic velocity is restrained, which displays a collimation behavior for specific spins and valleys. Therefore, the transmission presents strong spin- and valley-dependent feature, consistent with the band structure, resulting in a significant spin and valley polarizations. In addition, the disorder could greatly enhance the spin and valley polarizations. Finally, we hope these results can be conducive to the potential applications of the spin and valley indices.

Afkortingen

2D:: Tweedimensionaal
FM:: Ferromagnetic
SOI:: Spin-orbit interaction

Verminder de gevoeligheid van CL-20 door de thermische geleidbaarheid te verbeteren door middel van koolstofnanomaterialen Ultragevoelige reksensor op basis van flexibele piëzo-elektrische poly(vinylideenfluoride)film

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal