Een basis neuraal netwerk van Perceptron trainen

Dit artikel presenteert Python-code waarmee je automatisch gewichten kunt genereren voor een eenvoudig neuraal netwerk.

Welkom bij AAC's serie over Perceptron neurale netwerken. Als je vanaf het begin wilt beginnen voor achtergrondinformatie of vooruit wilt, bekijk dan de rest van de artikelen hier:

1. Hoe classificatie uitvoeren met behulp van een neuraal netwerk:wat is de Perceptron?
2. Een eenvoudig Perceptron neuraal netwerkvoorbeeld gebruiken om gegevens te classificeren
3. Een basis Perceptron neuraal netwerk trainen
4. Eenvoudige neurale netwerktraining begrijpen
5. Een inleiding tot trainingstheorie voor neurale netwerken
6. De leersnelheid in neurale netwerken begrijpen
7. Geavanceerde machine learning met de meerlaagse Perceptron
8. De Sigmoid-activeringsfunctie:activering in meerlaagse Perceptron neurale netwerken
9. Een meerlagig Perceptron neuraal netwerk trainen
10. Trainingsformules en backpropagation voor meerlaagse perceptrons begrijpen
11. Neurale netwerkarchitectuur voor een Python-implementatie
12. Hoe maak je een meerlaags Perceptron neuraal netwerk in Python
13. Signaalverwerking met behulp van neurale netwerken:validatie in neuraal netwerkontwerp
14. Trainingsdatasets voor neurale netwerken:een neuraal netwerk met Python trainen en valideren

Classificatie met een enkellaags Perceptron

Het vorige artikel introduceerde een eenvoudige classificatietaak die we hebben onderzocht vanuit het perspectief van op neurale netwerken gebaseerde signaalverwerking. De wiskundige relatie die voor deze taak nodig was, was zo eenvoudig dat ik het netwerk kon ontwerpen door alleen maar na te denken over hoe een bepaalde set gewichten het uitvoerknooppunt in staat zou stellen de invoergegevens correct te categoriseren.

Dit is het netwerk dat ik heb ontworpen:

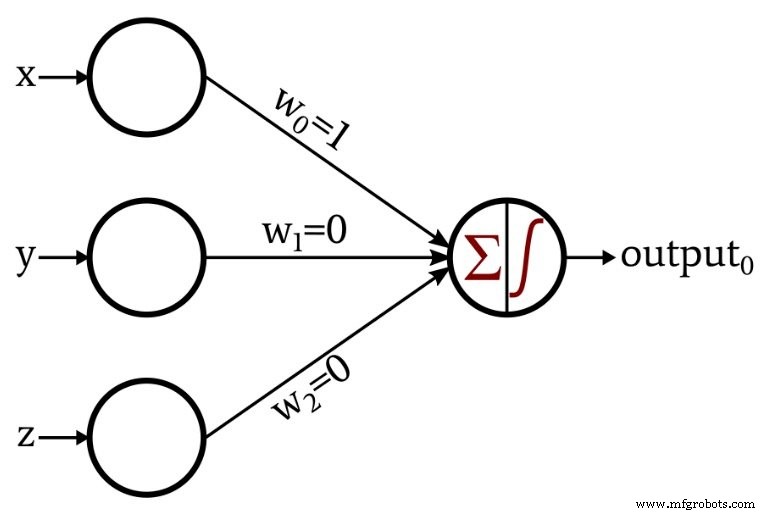
De activeringsfunctie in het uitgangsknooppunt is de eenheidsstap:

\[f(x)=\begin{cases}0 &x <0\\1 &x \geq 0\end{cases}\]

De discussie werd een beetje interessanter toen ik een netwerk presenteerde dat zijn eigen gewichten creëerde via de procedure die bekend staat als training:

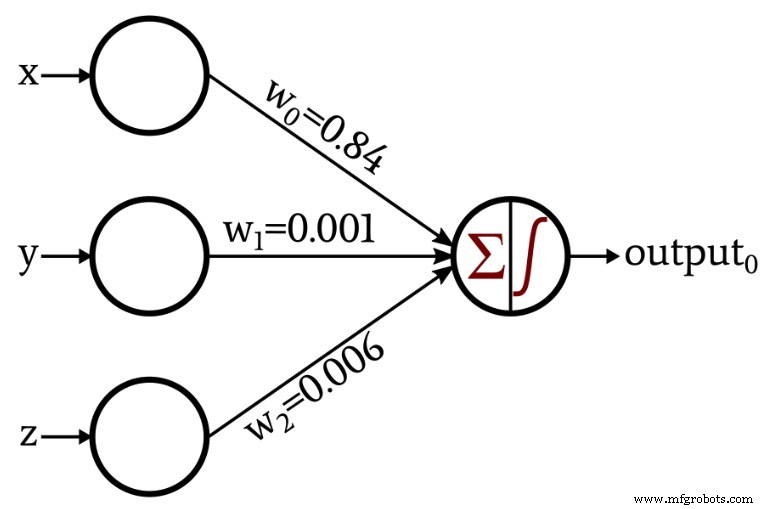
In de rest van dit artikel zullen we de Python-code onderzoeken die ik heb gebruikt om deze gewichten te verkrijgen.

Een Python neuraal netwerk

Hier is de code:

panda's importeren importeer numpy als np input_dim =3 learning_rate =0.01 Gewichten =np.random.rand(input_dim) #Gewichten[0] =0,5 #Gewichten[1] =0,5 #Gewichten[2] =0,5 Training_Data =pandas.read_excel("3D_data.xlsx") Expected_Output =Training_Data.output Training_Data =Training_Data.drop(['output'], axis=1) Training_Data =np.asarray(Training_Data) training_count =len(Training_Data[:,0]) voor tijdperk in bereik (0,5):voor datum in bereik (0, training_count):Output_Sum =np.sum(np.multiply(Training_Data[datum,:], Gewichten)) als Output_Sum <0:Uitvoerwaarde =0 anders:Uitvoerwaarde =1 error =Expected_Output[datum] - Output_Value voor n in bereik (0, input_dim):Gewichten[n] =Gewichten[n] + leertempo*fout*Training_Data[datum,n] print("w_0 =%.3f" %(Gewichten[0])) print("w_1 =%.3f" %(Gewichten[1])) print("w_2 =%.3f" %(Gewichten[2])) 

Laten we deze instructies eens nader bekijken.

Het netwerk configureren en gegevens ordenen

input_dim =3

De dimensionaliteit is instelbaar. Onze invoergegevens bestaan, als u zich herinnert, uit driedimensionale coördinaten, dus we hebben drie invoerknooppunten nodig. Dit programma ondersteunt geen meerdere uitvoerknooppunten, maar we zullen in een toekomstig experiment instelbare uitvoerdimensionaliteit opnemen.

learning_rate =0,01

We zullen het leertempo bespreken in een toekomstig artikel.

Gewichten =np.random.rand(input_dim) #Gewichten[0] =0,5 #Gewichten[1] =0,5 #Weights[2] =0,5

Gewichten worden doorgaans geïnitialiseerd op willekeurige waarden. De numpy random.rand() functie genereert een array van lengte input_dim gevuld met willekeurige waarden verdeeld over het interval [0, 1). De initiële gewichtswaarden zijn echter van invloed op de uiteindelijke gewichtswaarden die door de trainingsprocedure worden geproduceerd, dus als u de effecten van andere variabelen (zoals de grootte van de trainingsset of de leersnelheid) wilt evalueren, kunt u deze verstorende factor verwijderen door alle instellingen in te stellen. gewichten naar een bekende constante in plaats van een willekeurig gegenereerd getal.

Training_Data =pandas.read_excel("3D_data.xlsx")

Ik gebruik de Panda's-bibliotheek om trainingsgegevens uit een Excel-spreadsheet te importeren. Het volgende artikel gaat dieper in op de trainingsgegevens.

Expected_Output =Training_Data.output Training_Data =Training_Data.drop(['output'], axis=1)

De trainingsgegevensset bevat invoerwaarden en bijbehorende uitvoerwaarden. De eerste instructie scheidt de uitvoerwaarden en slaat ze op in een aparte array, en de volgende instructie verwijdert de uitvoerwaarden uit de trainingsgegevensset.

Training_Data =np.asarray(Training_Data) training_count =len(Training_Data[:,0])

Ik converteer de trainingsgegevensset, die momenteel een panda-gegevensstructuur is, in een numpy-array en kijk vervolgens naar de lengte van een van de kolommen om te bepalen hoeveel gegevenspunten beschikbaar zijn voor training.

Uitvoerwaarden berekenen

voor tijdperk binnen bereik(0,5):

De lengte van een trainingssessie wordt bepaald door het aantal beschikbare trainingsgegevens. U kunt echter doorgaan met het optimaliseren van de gewichten door het netwerk meerdere keren te trainen met dezelfde dataset. De voordelen van training verdwijnen niet simpelweg omdat het netwerk deze trainingsgegevens al heeft gezien. Elke volledige passage door de hele trainingsset wordt een tijdperk genoemd.

voor datum binnen bereik(0, training_count):

De procedure in deze lus vindt één keer plaats voor elke rij in de trainingsset, waarbij "rij" verwijst naar een groep invoergegevenswaarden en de bijbehorende uitvoerwaarde (in ons geval bestaat een invoergroep uit drie getallen die x, y vertegenwoordigen , en z componenten van een punt in de driedimensionale ruimte).

Output_Sum =np.sum(np.multiply(Training_Data[datum,:], Gewichten))

Het uitvoerknooppunt moet de waarden optellen die door de drie invoerknooppunten worden geleverd. Mijn Python-implementatie doet dit door eerst een elementgewijze vermenigvuldiging uit te voeren van de Training_Data-array en de Gewichten array en berekent vervolgens de som van de elementen in de array die door die vermenigvuldiging zijn geproduceerd.

als Output_Sum <0:Uitvoerwaarde =0 anders:Output_Value =1

Een if-else-instructie past de unit-step-activeringsfunctie toe:als de sommatie kleiner is dan nul, is de waarde die wordt gegenereerd door het uitvoerknooppunt 0; als de sommatie gelijk is aan of groter is dan nul, is de uitvoerwaarde één.

Gewichten bijwerken

Wanneer de eerste uitvoerberekening is voltooid, hebben we gewichtswaarden, maar deze helpen ons niet om classificatie te bereiken, omdat ze willekeurig worden gegenereerd. We maken van het neurale netwerk een effectief classificatiesysteem door de gewichten herhaaldelijk te wijzigen, zodat ze geleidelijk de wiskundige relatie tussen de invoergegevens en de gewenste uitvoerwaarden weerspiegelen. Gewichtsaanpassing wordt bereikt door de volgende leerregel toe te passen voor elke rij in de trainingsset:

\[w_{new} =w+(\alpha\times(output_{expected}-output_{calculated})\times input)\]

Het symbool \( \alpha \) geeft de leersnelheid aan. Dus om een ​​nieuwe gewichtswaarde te berekenen, vermenigvuldigen we de corresponderende invoerwaarde met de leersnelheid en met het verschil tussen de verwachte output (die wordt geleverd door de trainingsset) en de berekende output, en dan wordt het resultaat van deze vermenigvuldiging opgeteld tot de huidige gewichtswaarde. Als we delta definiëren (\(\delta\) ) als (\(output_{expected} - output_{calculated}\)), we kunnen dit herschrijven als

\[w_{new} =w+(\alpha\times\delta\times input)\]

Dit is hoe ik de leerregel in Python heb geïmplementeerd:

error =Expected_Output[datum] - Output_Value voor n in bereik (0, input_dim):Gewichten[n] =Gewichten[n] + learning_rate*error*Training_Data[datum,n]

Conclusie

U hebt nu code die u kunt gebruiken voor het trainen van een Perceptron met één laag en één uitvoerknooppunt. In het volgende artikel zullen we meer details over de theorie en praktijk van neurale netwerktraining onderzoeken.