Modellen van banden barsten in de kleine overlap frontale crashsimulaties

Bij een frontale botsing met een kleine overlap worden de buitenranden van het voertuig niet goed beschermd door de kreukelzonestructuren , vormen het belangrijkste lastdragende pad. Banden en wielen, evenals het veersysteem, worden meestal onderworpen aan de impactkracht. De banden die door de stijve barrière worden geraakt, barsten meestal door het scheuren van de band en het wiel en verliezen ook hun luchtafdichtingen door de parels te verwijderen. Het barsten van de band heeft invloed op de kinematica en vervorming van de ophanging van het voertuig en bijgevolg op de crashprestaties van het voertuig.

Het is belangrijk om rekening te houden met de drukdaling als gevolg van het barsten van de band voor een nauwkeurige voorspelling van de reactie van het voertuig op een ongeval. Daarom is het modelleren van de bandbreuk die wordt veroorzaakt door materiële schade en/of het verwijderen van parels als gevolg van verlies van afdichting tussen band en velg van cruciaal belang om het ongeval met kleine overlap na te bootsen. Dit artikel presenteert de eindige-elementenmodellering van banden in Abaqus om rekening te houden met het barsten van banden in crashsimulaties.

Bandenmodellering

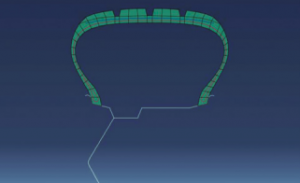
De eerste stap is het creëren van een tweedimensionaal axisymmetrisch bandenspanningsmodel. Dit omvat het modelleren van het loopvlak en de zijwand van de band met behulp van axisymmetrische massieve elementen; het modelleren van bandengordels en karkas met ingebedde axisymmetrische oppervlakte-elementen; en het wiel met axisymmetrische schaalelementen.

De tweede stap is het genereren van een symmetrisch driedimensionaal bandenmodel door het tweedimensionale model aan het einde van de inflatieanalyse 360 ​​graden rond te draaien. Met de parameter “FILE NAME” van de optie *SYMMETRIC MODEL GENERATION in Abaqus/Standard wordt een driedimensionaal model met de extensie .axi gemaakt. Dit bestand bevat de knoop-, element- en sectiedefinities.

Modellen van bandbreuk

Het belangrijkste kenmerk om de bandbreuk te repliceren, is het modelleren van de twee faalmechanismen:materiaalbreuken in band en velg en het verwijderen van parels. Daarom moeten de volgende wijzigingen worden aangebracht aan het driedimensionale bandenmodel:De zijwand van de band en de velg moeten als twee afzonderlijke delen worden gemodelleerd om scheiding mogelijk te maken om rekening te houden met de pareling. De stalen hiel moet zo worden gemodelleerd dat er voldoende weerstand en wrijving is om de band intact te houden wanneer deze is opgepompt met de aanbevolen bandenspanning. Hier modelleren we de bandhiel met behulp van 3D-balkelementen.

De materiaaleigenschappen van het loopvlak en de zijwand van de band moeten de destructieve schade van het rubbermateriaal bij een botsing kunnen opvangen en zo openingen in de band creëren waardoor lucht buiten de band kan ontsnappen en barsten. Afhankelijk van de omstandigheden, zoals de impacthoek en de impactsnelheid, kunnen beide mechanismen de band doen barsten. Welke van de twee mechanismen het eerst ook gebeurt - materiaalbreuk en kralenverwijdering - zal worden gevolgd door het barsten van de band en een snelle daling van de bandenspanning en verlies van steun aan de ophanging van het voertuig.

De Abaqus-vloeistofholtefunctie wordt gebruikt om de interne druk van de band te modelleren. Een gesloten volume wordt gedefinieerd door oppervlakte-elementen te gebruiken die de binnenkant van de band en de velg bedekken door knooppunten te delen met de interne laag knooppunten van de band en de velg. De druk van de band is gerelateerd aan het gesloten volume. Om het materiaalfalen te verklaren, gebruiken we het hyperelastische materiaal samen met schadecriteria voor de rubberen materiaaleigenschappen van het loopvlak en de zijwand. Bij materiële beschadiging en verwijdering van het element zullen de oppervlakte-elementen die onder het rubbermateriaal liggen vrij zijn om door het drukverschil buiten de band te worden geduwd.

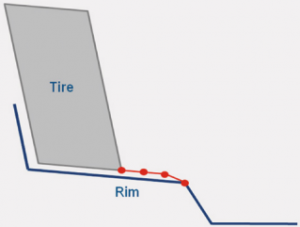
Het volume van de vloeistofholte neemt snel toe en de bandenspanning neemt af naarmate het volume toeneemt. Om rekening te houden met het verwijderen van de kralen, moet het gebied dat de band in contact komt met de velg als volgt worden gemodelleerd:fijner gaas, waardoor twee lagen vrije knopen ontstaan ​​op het gesloten volume van de vloeistofholte. Twee ringen van schaalelementen met verwaarloosbare materiaalstijfheid worden toegevoegd, die knooppunten delen met de twee ringen van oppervlakte-elementen. Er wordt contact gemaakt tussen de twee ringen van schaalelementen en de velg om de vrije knopen op hun plaats te houden wanneer band en velg niet gescheiden zijn.

De vrije knooppunten zijn verschoven om te voorkomen dat ze zich op dezelfde locatie als de rand bevinden voor betere contactomstandigheden. Wanneer de kralen worden verwijderd, kunnen de vrije knooppunten vrij door de opening gaan, waardoor het volume groter wordt en de band drukloos wordt. De rode lijnen komen overeen met de oppervlakte-elementen met onderliggende schaalelementen die de opening tussen de band en de velg dichten, waardoor een gesloten volume voor de vloeistofholte ontstaat.

Simulatieresultaten

Verticale impact, zijdelingse impact en een impact van 45 graden werden gesimuleerd. Gebleken is dat bij de verticale botsing, wanneer het botslichaam contact maakt met de band op het loopvlak van de band, het rubbermateriaal beschadigt waar de velg ook contact maakt met het loopvlak van de band. Het barsten van de band volgt met een snelle drukval. Bij een zijdelingse botsing wanneer het botslichaam contact maakt met de zijwand van de band, scheidt de zijwand van de velg. Het barsten van de band volgt met een snelle drukval. Bij een botsing van 45 graden treedt zowel materiële schade als pareling op, waardoor de bandenspanning afneemt.

Materiaalstoring deed zich eerst voor op ongeveer 4 msec en het verwijderen van kralen volgt op ongeveer 4,5 msec aan de andere kant van de band waarbij de velg door de impact sneller beweegt dan de bandwand. De drukcurve van de vloeistofholte wordt verkregen uit de simulatie. Het blijkt dat de druk blijft toenemen nadat materiële schade door ontsnappende lucht nog steeds lager is dan de drukverhoging door impact. Maar na 0,5 msec begint de druk te dalen. De band loopt volledig leeg bij ongeveer 5,5 msec. Het barstproces duurt in totaal 1,5 msec vanaf het eerste optreden van materiaalfalen tot nuldruk.

Wilt u meer weten?

Klik hier om onze trainingen te bekijken en te registreren.