Stelling van Millman - AC- en DC-circuits analyseren - voorbeelden

Theorema van Millman voor AC- en DC-circuits - stap voor stap opgeloste voorbeelden

Theorema van Millman

De stelling van Millman wordt gebruikt in de circuitanalyse wanneer deze alleen parallelle vertakkingen heeft. Daarom is deze stelling nuttig om de spanning aan het einde van een circuit te berekenen. De stelling van Millman is alleen van toepassing op het circuit dat een parallel netwerk bevat.

De stelling van Millman is een combinatie van De stelling van Thevenin en De stelling van Norton . Soms wordt deze stelling ook wel Parallelle Generator Stelling . genoemd . Deze stelling is voorgesteld door professor elektrotechniek Jacob Millman . En naar zijn naam wordt deze stelling de stelling van Millman genoemd.

De stelling van Millman stelt dat;

Het betekent dat we de spanning over de parallelle takken van het gegeven netwerk kunnen vinden. Deze stelling vermindert de complexiteit van het netwerk wanneer een aantal bronnen is aangesloten, zoals weergegeven in de onderstaande afbeelding.

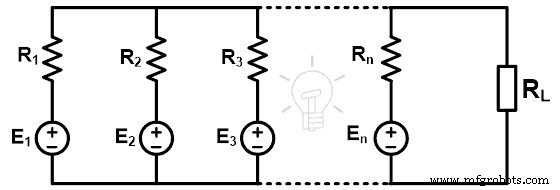
Volgens de stelling van Millman; de spanning over de belasting is;

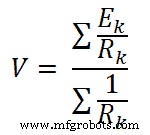
• Gerelateerde post:Thevenin's Theorema. Stap voor stap handleiding met opgelost voorbeeld

Wiskundige vergelijking

Zoals in de bovenstaande afbeelding wordt getoond, heeft het circuit een n-aantal spanningsbronnen (E₁ , E₂ , E₃ , …, E_n ). En de interne weerstand van de bronnen is R₁ , R₂ , R₃ , ..., R_n respectievelijk. Volgens de stelling van Millman kan elk circuit worden vervangen door het onderstaande netwerk. De volgende afbeelding toont het equivalente circuit van Millman.

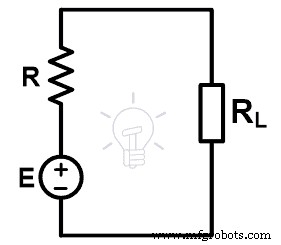
Nu moeten we de waarde van de spanningsbron (E) en de equivalente weerstand (R) vinden. Het bovenstaande circuit is vergelijkbaar met het equivalente circuit van Thevenin. Daarom kunnen we zeggen dat de spanningsbron (E) hetzelfde is als de equivalente spanning van Thevenin (V_TH ) en de equivalente weerstand is de equivalente weerstand van Thevenin (R_TH ).

We vinden het equivalente circuit van Norton om een ​​eenvoudige berekening te maken. Daarvoor maken we een brontransformatie. En zet alle spanningsbronnen om in de stroombronnen.

We hebben een interne weerstand die in serie is geschakeld met de spanningsbron. Na brontransformatie wordt de spanningsbron omgezet in de stroombron en wordt de interne weerstand parallel geschakeld met de stroombron. Daarom wordt het bovenstaande circuit geconverteerd zoals weergegeven in de onderstaande afbeelding.

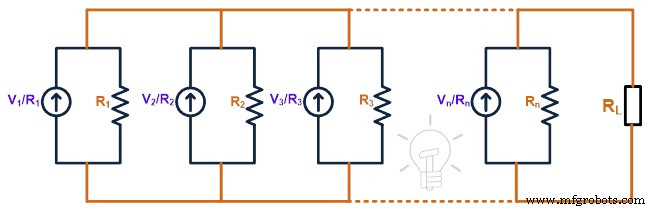
Volgens de wet van ohm zal de waarde van de huidige bronnen de E₁ /R₁ , E₂ /R₂ , E₃ /R₃ , …, E_n /R_n . Nu, om de equivalente stroom van Norton (I_N ), moeten we de laadklemmen kortsluiten. En zoek de stroom die door die tak gaat.

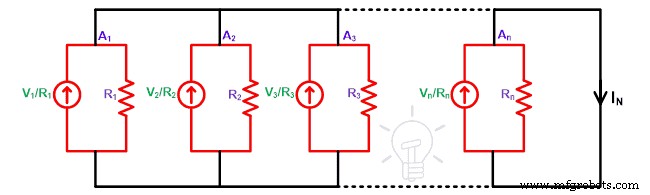
Bij knooppunt A₁ , verdeelt de stroom zich in twee paden. Eén pad is door de weerstand R₁ en het tweede pad is van de kortgesloten tak. Zoals we weten, stroomt de stroom altijd door het pad met lage weerstand. Daarom gaat in deze toestand de volledige stroom door de kortgesloten tak. En de stroom die door de weerstand gaat is nul.

Ditzelfde gebeurt voor alle bronnen op knooppunt A₂ , A₃ , …, A_n . En de stroom die door alle weerstanden gaat, is nul.

Nu, bij knooppunt A₂ , de stroom afkomstig van knoop A₁ is toegevoegd. Evenzo, bij knooppunt A3, de stroom afkomstig van knooppunt A₂ is toegevoegd. Daarom, bij knooppunt A_n , stroom van alle toegevoegde knooppunten. De totale stroom is een optelling van alle stroom en staat bekend als de stroom van Norton (I_N ).

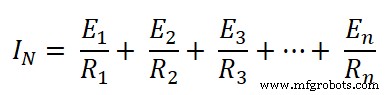
We hebben dus de equivalente stroom van Norton gevonden. Nu moeten we de equivalente weerstand van Norton vinden. En daarvoor moeten we alle in het circuit aanwezige energiebronnen verwijderen door de stroombron te openen en de spanningsbron kort te sluiten.

In de bovenstaande afbeelding hebben we alleen een huidige bron. We zullen deze stroombronnen verwijderen door middel van open circuits. En we moeten de belasting verwijderen om de equivalente weerstand te berekenen. Daarom ziet het resterende circuit eruit als de onderstaande afbeelding.

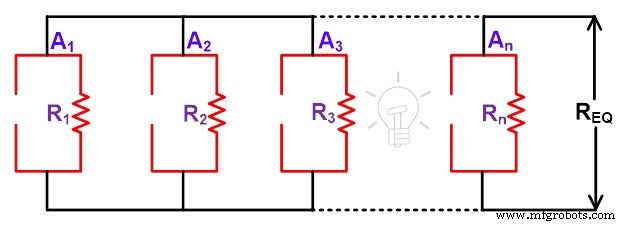
Zoals in de bovenstaande afbeelding te zien is, kunnen we zien dat alle weerstanden parallel zijn geschakeld. En deze parallelle combinatie is gelijk aan de equivalente weerstand.

R_eq =R_N =R ₁ || R ₂ || R ₃ … || R_n

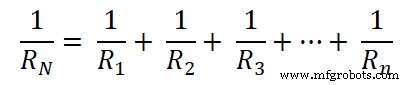
Plaats deze waarden nu in het equivalente circuit van Norton, zoals weergegeven in de onderstaande afbeelding.

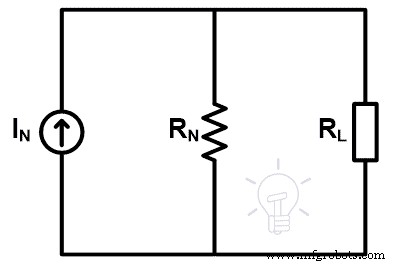
Als we het equivalente circuit van Norton omzetten in het equivalente circuit van Thevenin, kunnen we de waarde van E en R berekenen uit de stroomsterkte van Norton I_N en Norton Resistance R_N .

Volgens de wet van Ohm;

E =I_N x R_N

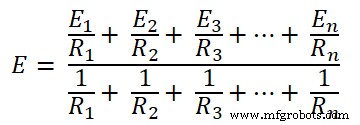
Laten we de bovenstaande vergelijking in algemene vorm maken voor n-aantal vertakkingen.

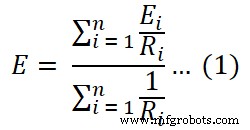
We hebben dus de waarde van de spanningsbron. En de waarde van equivalente weerstand is gelijk aan Norton's equivalente weerstand. We kunnen dus het equivalente circuit van Millman krijgen (fig-2).

• Gerelateerde post:de stelling van Norton. Stap voor stap handleiding met opgelost voorbeeld

Te volgen stappen voor de Millman-stelling

Stap-1 De stelling van Milliman is de enige die van toepassing is op het netwerk of circuit met een groter aantal parallelle takken. We nemen dus aan dat we het circuit moeten oplossen met een aantal parallelle takken met een spanningsbron die in serie is geschakeld met de interne weerstand.

Stap-2 Maak een lijst van de interne weerstand of weerstand die in serie is geschakeld en de spanningsbronnen.

Stap-3 Vind de equivalente weerstand (R) over de laadklemmen met kortsluiting van de spanningsbronnen.

Stap-4 Pas de stelling van Millman toe en vind de waarde van spanning (E) over de laadklemmen. Gebruik daarvoor vergelijking-1. Deze spanning is de spanning over de belasting.

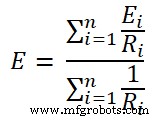
Stap-5 Zet de waarde van R en E in het equivalente circuit van Millman (fig-2).

Stap-6 Pas KVL toe op de lus om de stroom door de belasting te vinden.

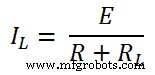
• Verwante post:Superpositiestelling - Circuitanalyse met opgelost voorbeeld

DC-circuit analyseren met behulp van de stelling van Millman

Voorbeeld #1

Zoek de stroom en spanning over de laadterminal met behulp van de stelling van Millman.

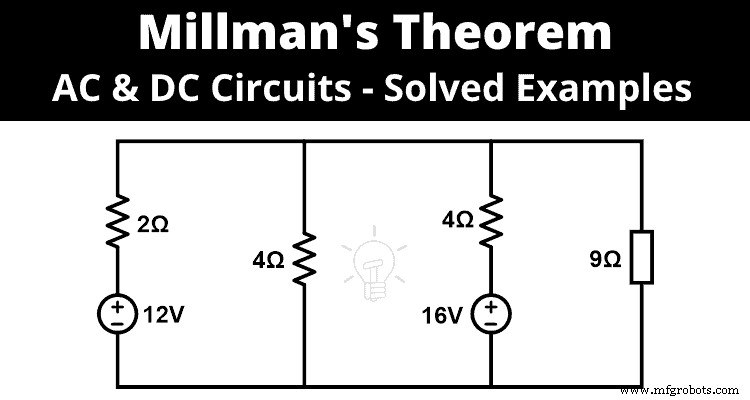
Stap-1 Door de bovenstaande figuur te observeren, kunnen we zeggen dat alle vier takken parallel zijn verbonden. En we kunnen de stelling van Millman toepassen.

Stap-2 Er zijn drie takken behalve de belastingtak. Er zijn dus drie spanningen en drie weerstanden zoals hieronder vermeld.

E ₁ =12V en R ₁ =2Ω

E ₂ =0V en R ₁ =4Ω

E ₃ =16V en R ₁ =4Ω

Stap-3 Om de equivalente weerstand te vinden, moeten we de spanningsbronnen verwijderen door kortsluiting te maken en de laadklemmen te openen. Daarom wordt het resterende cijfer weergegeven in de onderstaande afbeelding.

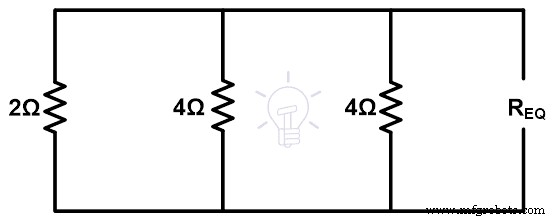
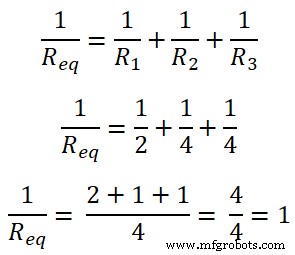
R_eq =1Ω

Zoals in de bovenstaande afbeelding te zien is, zijn alle weerstanden parallel. Dus de equivalente weerstand is;

Stap-4 Pas nu de stelling van Millman toe.

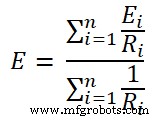
In dit voorbeeld hebben we 3 vertakkingen. Daarom gebruiken we n=3.

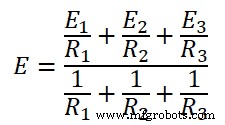
Zet de hierboven vermelde waarden in deze vergelijking.

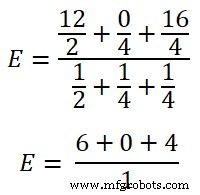
E =10V

Dit is de spanning over de laadaansluiting.

Stap-5 Zet deze waarden in het equivalente circuit van Millman.

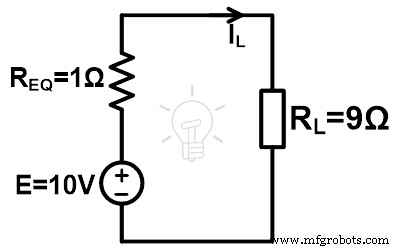
Stap-6 Volgens de wet van ohm,

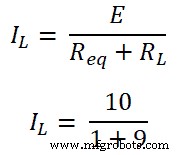
I_L =1A

Daarom is de spanning over de belasting 10 V en de stroom die door de belasting gaat is 1 A.

• Gerelateerde post:Stelling van Tellegen - opgeloste voorbeelden en MATLAB-simulatie

AC-circuit analyseren met behulp van de stelling van Millman

Voorbeeld #2

Zoek de stroom en spanning over de laadklemmen met behulp van de stelling van Millman.

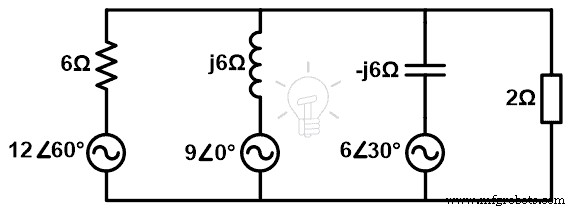
Stap-1 Zoals in de bovenstaande afbeelding te zien is, zijn vier takken parallel geschakeld. Daarom kunnen we de stelling van Millman toepassen.

Stap-2 Als we de belastingtak niet beschouwen, zijn er drie takken. Om de berekening gemakkelijk te maken, zullen we de spanningen en impedantie opsommen. In het geval van een wisselstroomcircuit moeten we woordimpedantie gebruiken in plaats van weerstand.

De waarden van spanningsbronnen worden in polaire vorm gegeven. Maar de waarden van impedanties worden gegeven in de rechthoekige vorm. We moeten dus de waarden van de spanningsbron in polaire vorm omzetten.

V ₁ =12∠60° =6 + j 10.392

V ₂ =9∠0° =9 + j 0

V ₃ =6∠30° =5.196 + j 3

Impedanties worden gegeven in rechthoekige vormen. Dus we vermelden het zoals het is.

Z ₁ =6Ω

Z ₂ =j 6Ω

Z ₃ =–j 6Ω

Stap-3 Zoek de equivalente impedantie. Zoals in het bovenstaande voorbeeld te zien is, moeten we alle spanningsbronnen verwijderen door kortsluiting. En het resterende circuit is zoals weergegeven in de onderstaande afbeelding.

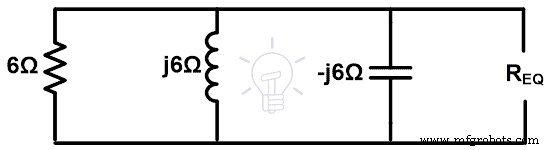
Hier zijn alle impedanties parallel geschakeld. De equivalente impedantie zal dus zijn;

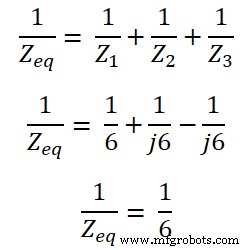
Z _eq =6Ω

Stap-4 Pas nu de stelling van Milliman toe,

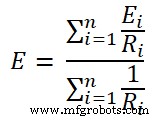
Hier hebben we drie takken. Daarom is n gelijk aan 3.

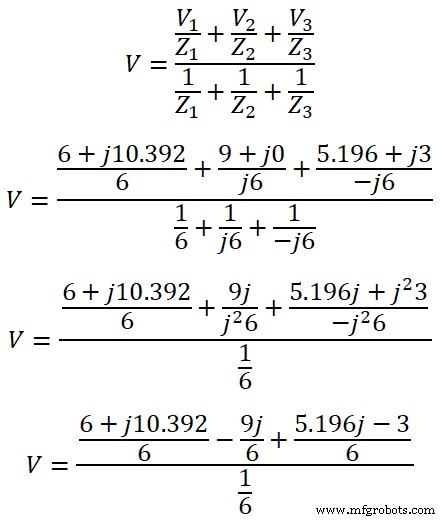
V =6 + 1j 0.392 – j 9 + j 5.196 – 3

V =3 + j 6.588

Nu moeten we de RMS-waarde vinden.

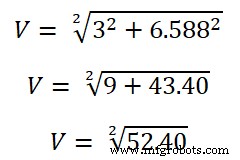
V =7.23V

Stap-5 Zet deze waarden in het equivalente circuit van Millman.

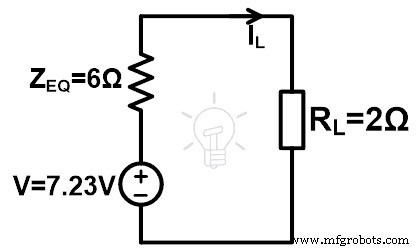
Stap-6 Volgens de wet van ohm,

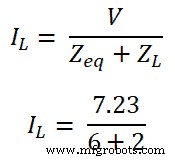
I_L =0,9A

• Gerelateerde post: Maximale vermogensoverdrachtstelling voor AC- en DC-circuits
  

Beperking van de stelling van Millman

De stelling van Millman is erg handig om het netwerk op te lossen. Maar er is een beperking die hieronder wordt vermeld.

• Deze stelling is niet van toepassing op het circuit met een afhankelijke bron tussen de onafhankelijke bron.
• Voor het circuit met minder dan twee onafhankelijke bronnen is deze stelling niet bruikbaar.
• Deze stelling is niet van toepassing op het circuit met alleen serie-elementen.
• Als er een element is verbonden tussen de bron, kan deze stelling niet van toepassing zijn.

Toepassingen van de stelling van Millman

De stelling van Millman wordt veel gebruikt in de netwerkanalyse om complexe circuits op te lossen. De toepassing van de stelling van Millman is zoals hieronder vermeld.

• De stelling van Millman is het meest bruikbaar om de spanning en stroom van de belastingsimpedantie te vinden in het geval dat er een groter aantal parallelle takken beschikbaar is met een aantal spanningsbronnen.
• De berekening van deze stelling is eenvoudig. Het is niet nodig om meer vergelijkingen te gebruiken.
• Deze stelling wordt gebruikt om het complexe circuit op te lossen met complexe elementen zoals Op-Amp.

Verwante handleidingen voor analyse van elektrische circuits:

• SUPERNODE-circuitanalyse - stap voor stap met opgelost voorbeeld
• SUPERMESH-circuitanalyse - stap voor stap met opgelost voorbeeld
• Kirchhoff's stroom- en spanningswet (KCL &KVL) | Opgelost voorbeeld
• Cramer's Rule Calculator - 2 en 3 vergelijkingssysteem voor elektrische circuits
• Wheatstone Bridge – Circuit, werking, afleiding en toepassingen
• Elektrische en elektronische technische rekenmachines
• 5000+ elektrische en elektronische technische formules en vergelijkingen