Magische wiskundige relaties voor nanoclusters

Abstract

Grootte en oppervlakte-eigenschappen zoals katalyse, optische kwantumdot fotoluminescentie en oppervlakteplasmonresonanties zijn afhankelijk van de coördinatie en chemie van metalen en halfgeleidende nanoclusters. Dergelijke coördinatie-afhankelijke eigenschappen worden hierin gekwantificeerd via "magische formules" voor het aantal schillen, n , in het cluster. We onderzoeken face-centered kubieke, lichaams-gecentreerde kubieke, eenvoudige kubische clusters, hexagonale dicht opeengepakte clusters, en de diamant kubische structuur als een functie van het aantal clusterschillen, n . Daarnaast onderzoeken we de Platonische lichamen in de vorm van clusters met meerdere schillen, voor in totaal 19 clustertypes. Het aantal bindingen en atomen en coördinatiegetallen vertonen magische getalkenmerken versus n , naarmate de clusters groter worden. Beginnend met alleen de ruimtelijke coördinaten, creëren we een aangrenzendheids- en afstandsmatrix die de berekening van topologische indices vergemakkelijkt, inclusief de Wiener-, hyper-Wiener-, omgekeerde Wiener- en Szeged-indices. Enkele bekende topologische formules voor sommige Platonische lichamen wanneer n =1 zijn rekenkundig geverifieerd. Deze indices hebben magische formules voor veel van de clusters. De eenvoudige kubische structuur is de minst complexe van onze clusters, gemeten aan de topologische complexiteit afgeleid van de informatie-inhoud van de hoekpunt-graadverdeling. De dispersie, of het relatieve percentage oppervlakte-atomen, wordt kwantitatief gemeten met betrekking tot grootte- en vormafhankelijkheid voor sommige typen clusters met katalytische toepassingen.

Inleiding

Magische getallen en formules voor nanoclusters hebben een lange geschiedenis die teruggaat tot de vooruitziende publicatie door van Hardeveld en Hartog in 1969 [1]. Hun inzichten dateerden van vóór het nanowetenschapstijdperk. Sindsdien hebben we magische getallen zien verschijnen in 2D-polygonen en 3D-veelvlakken [2], koolstoffullerenen [3], en in beperkte reikwijdte opnieuw in clusters [4]. Dergelijke uiteenlopende materialen zoals silicium [5], boor [6], en in feite meer dan 1000 publicaties van de indexeringsdienst "Web of Science" verwijzen naar magische getallen in clusters. De studie van de grootte en vorm van nanoclusters is belangrijk voor de huidige samenleving, omdat dit niet alleen de intrinsieke fysische en chemische eigenschappen bepaalt, maar ook de relevantie voor optische, katalytische, elektronische en magnetische toepassingen [7]. Ons doel is om de database van deze kennis bij te werken met huidige relaties en gegevens, nu we het nano-rijk zijn betreden.

Het optreden van magische getallen in nanoclusters heeft voornamelijk te maken met de vorming van schillen van atomen op een fundamentele cel. Wanneer het aantal atomen een volledige schaal voltooit, vinden we een unieke reeks getallen, 'magie' genaamd, die de schillen van atomen definieert. Een cluster wordt weergegeven door een grafiek met de atomen als hoekpunten en de bindingen als randen. Het bestaat uit geneste schelpen als lagen van een ui. We definiëren het aantal lagen als n en ontdek de wiskundige relaties van naaste buurcoördinatiegetallen, bindingen, het totale aantal atomen en enkele topologische indices als een functie van n . Het originele artikel van van Hardeveld en Hartog [1] beschouwde fcc-, bcc- en hcp-clusters. De verwijzing door Teo en Sloane [2] beschouwt veelvlakken en platonische lichamen, maar negeert de relatie van de coördinatiegetallen van de naaste buren. We voegen aan deze database toe door te kijken naar eenvoudige kubieke, diamant kubieke en de Platonische lichamen, naast de topologische eigenschappen en dispersie van de clusters.

De overgang in grootte van bulk naar clusters van een paar atomen gaat eigenlijk over de relatie van de oppervlakte-atomen in vergelijking met bulkatomen. Eigenschappen zoals katalytische chemie, oppervlakte-plasmonresonantie en optische kwantumdot-fotoluminescentie [8] worden beïnvloed door de coördinatie en het aantal oppervlakte-atomen. De dispersie of het relatieve percentage oppervlakte-atomen wordt bepaald door de verhouding van oppervlakte-atomen tot het totale aantal atomen, zoals eerder is overwogen [9]. Onze analyse zal de relatieve rangorde van de dispersie bepalen in termen van clustergeometrie.

Topologische indices begonnen met het originele artikel van Wiener over zijn index en de kookpunten van paraffine [10]. Pas enige tijd later introduceerde Hosoya een wiskundig formalisme om topologische indices te analyseren [11]. We hebben eerder topologische indices en nanoclusters geïntroduceerd [12]. Op het moment dat ik dit schrijf, bestaan er veel indices, waarvan sommige afhankelijk zijn van de matrix van nabijheid of afstand. We laten hier zien dat in veel van de clustervormen magische wiskundige relaties bestaan voor de vier indices als functie van n en het aantal schelpen.

Methoden

Voor elk van de soorten clusters die we bestuderen, creëren we een rekenalgoritme dat de atomaire coördinaten van de clusters bepaalt. Vervolgens gaan we verder met het maken van een aangrenzende matrix en een afstandsmatrix die als volgt is gedefinieerd. Een aangrenzende matrix A wordt gemaakt waar we i . definiëren en j als naaste buren en scheid ze van de rest door te eisen dat r _ij <r _c , waar r _c is een drempelwaarde, iets boven de dichtstbijzijnde buurafstand, maar kleiner dan de tweede buurafstand. Dus

$$ \mathbf{A}(i,j)=\left\{\begin{array}{l} 1~~ \text{if}~ r_{ij} waar r _ij is de Euclidische afstand tussen atoom i en atoom j . Een geschikte waarde voor r _c is 1.32·r _min , waar r _min is de kleinste bindingslengte. Dit geldt zowel voor de dodecaëdrische structuur als voor de andere die we bestuderen. De coördinatiegetallen van het cluster zijn eenvoudig het aantal niet-nul-elementen in een kolom van de aangrenzende matrix. De afstandsmatrix wordt gedefinieerd als

$$ \mathbf{D}(i,j) =\left\{\begin{array}{ll} 0 &i =j \\ d_{ij} &i \neq j \end{array}\right. $$ (2)

waar d _ij is de lengte van het kortste pad in de grafiek van i naar j . Er bestaat een efficiënt algoritme voor de berekening van de afstandsmatrix uit de aangrenzende matrix [13]. Met behulp van deze definities kunnen we de Wiener-index berekenen, W (G ), de hyper-Wiener-index, W W (G ), de omgekeerde Wiener-index rW (G ), en de Szeged-index, Sz (G ), zoals eerder beschreven [14]. Deze berekeningen gebruiken hetzelfde algoritme dat we eerder hebben gebruikt voor topologische indices en nanoclusters [12].

Eerdere auteurs hebben bewijzen van magische relaties geleverd, die we in onze notatie samenvatten, relevant voor het hier gepresenteerde werk [1, 2]. Omdat we matrices voor naaste buren maken, kennen we het coördinatiegetal c n _ik van hoekpunt i door de elementen van A . op te tellen (ik ,:). Onze structuur bestaat uit n +1 schelpen genummerd 0,1,…,n . Zij $\phantom {\dot {i}\!}N_{{cn}_{i}}(n)$ het aantal atomen met coördinatie c n _ik waar 1≤c n _ik ≤c n _M met c n _M de maximale coördinatie in het cluster. Dan wordt het totale aantal atomen in de cluster gegeven door

$$ N_{T}(n) =\sum_{{cn}_{i}=1}^{{cn}_{M}}{N_{{cn}_{i}}(n)}. $$ (3)

De oppervlakte-atomen in de buitenste schil n een set bindingen hebben die kleiner is dan de bulkcoördinatie. Dus de maximale coördinatie voor oppervlakte-atomen is c n _s <c n _M , en het aantal oppervlakte-atomen is

$$ N_{S}(n) =\sum_{{cn}_{i}=1}^{{cn}_{s}}{N_{{cn}_{i}}(n)}. $$ (4)

Dit geldt als alle niet-oppervlaktehoeken een coördinatie hebben die groter is dan c n _s , wat geldt voor alle clusters, maar let op de discrepantie voor de dodecaëders hieronder. We bepalen de $\phantom {\dot {i}\!}N_{{cn}_{i}}(n)$ door de kolommen van de aangrenzende matrix te tellen waarvan de som c is n _ik . Merk op dat ons clustercoördinaatalgoritme is gebouwd door shells, zodat elke volgende shell alle eerdere lagere waarden van n bevat. . In figuur 1 illustreren we de schillen van de clusters voor een fcc-kubus en een dodecaëder. Bovendien is het aantal obligaties in het cluster

$$ N_{B}(n) =\frac{1}{2}\sum_{{cn}_{i}=1}^{{cn}_{M}}{{cn}_{i}\ cdot N_{{cn}_{i}}(n)}, $$ (5)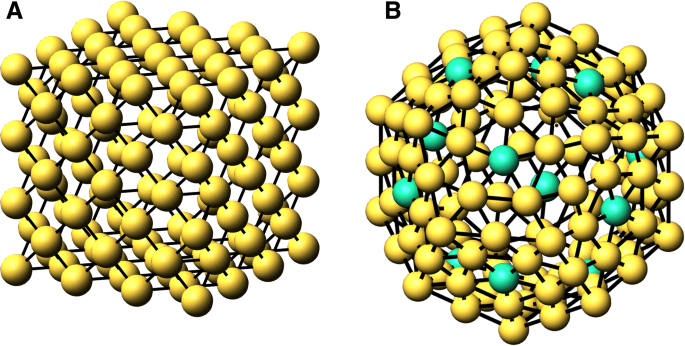

Schelpen van atomen voor n =3 voor A. fcc kubus en n =2 B. dodecaëder. In B verwijzen de groene atomen (12) naar c n =5 binnen de schaal

waar N _B (n ) is het aantal bindingen en c n _M is de maximale coördinatie. De factor 1/2 ontstaat door de paarsgewijze dichtstbijzijnde buurbinding. Deze magische relatie lijkt in eerdere publicaties niet te zijn overwogen, met uitzondering van enkele clusters die in [4] zijn onderzocht. We merken ook op dat Teo en Sloane het totale aantal atomen, oppervlakte-atomen en inwendige atomen voor clusters als volgt hebben afgeleid [2]:

$$ N_{T}(n) =\alpha n^{3}+\frac{1}{2}\beta n^{2}+\gamma n+1~~n\ge{0} $$ ( 6)

waar N _T (n ) is het totale aantal atomen, en

$$ \alpha =C/6 $$ (7)

waar C is het aantal tetraëdrische cellen waarin het veelvlak is verdeeld, en

$$ \beta =1/2F_{s} $$ (8)

waar F _s is het aantal driehoekige vlakken op het oppervlak, en

$$ \gamma =F_{s}/4+V_{i}+1-C/6 $$ (9)

waar V _ik is het aantal hoekpunten in het interieur. Ze laten ook zien dat

$$ N_{S}(n) =\beta n^{2}+2~~n\ge{1};~~N_{S}(0) =1 $$ (10)

$$ N_{I}(n) =N_{T}(n) - N_{S}(n), $$ (11)

waar N _Ik (n ) is het aantal inwendige atomen. Deze informatie (Vgl. (11)) is opgenomen in de aangrenzendheidsmatrix, evenals in Vgl. (3, 4, 5). Deze vergelijkingen zijn een controle van de resultaten van de aangrenzende matrixgegevens. Voor gecentreerde veelvlakken hebben we ook

$$ N_{I}(n) =N_{T}(n-1), $$ (12)

en van vgl. (11), we hebben

$$ N_{T}(n)=N_{S}(n)+N_{S}(n-1)+... +N_{S}(1)+N_{S}(0). $$ (13)

Uit deze vergelijkingen kunnen we de magische formules voor elk van de clusters als volgt afleiden. Na het berekenen van de topologische (0,1)-aangrenzend matrix A voor een cluster met n schelpen zoals beschreven, weten we dat de grootte N =N _T (n ) geeft het totale aantal atomen aan. De som van de items in kolom i geeft het aantal bindingen c n _ik (n ) voor atoom i en het tellen van het aantal kolomsommen gelijk aan c n _ik (n ) geeft duidelijk $\phantom {\dot {i}\!}N_{{cn}_{i}}(n)$. Omdat we weten dat deze afhankelijk zijn van n als polynoom van graad 3 kunnen we N . berekenen _T (n ) en c n _ik (n ) voor 4 opeenvolgende waarden van n , zeg n =n ₀ +j , j =0,1,2,3. Een eenvoudig interpolerend polynoom geeft dan de polynoomcoëfficiënten. Er moet worden geverifieerd dat door n . te verhogen ₀ , wat meestal gelijk is aan 1, veranderen de formules niet. Als de formules stabiel worden vanaf n ₀ aan, dan blijven ze geldig voor n ≥n ₀ . In sommige gevallen geldt de polynoomrelatie alleen voor de even n waarden of de oneven. Voor de fcc ruitvormige dodecaëder (tabel 1) hebben de opeenvolgende schillen bijvoorbeeld acht atomen met coördinatie 3 wanneer n ≥2 is even, en geen als n is vreemd. In dergelijke gevallen gelden verschillende polynomiale relaties voor n even en n vreemd, maar de gegevens worden gebruikt voor n =n ₀ +j , j =0,2,4,6 met n ₀ oneven (bijv. n ₀ =1) of n ₀ even (n ₀ =2). Om de exacte rationale coëfficiënten te krijgen, moet men het Vandermonde-systeem voor de coëfficiënten in exacte rekenkunde oplossen met behulp van de symbolische toolbox van MATLAB. Dit is hoe de tabellen 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 en 19 worden berekend. In de volgende sectie bepalen we magische formules voor N _T (n ), N _B (n ), en voor $\phantom {\dot {i}\!}N_{{cn}_{i}}(n)$ volgens het voorgeschreven recept.

De dispersie (belichte fractie, FE) van de oppervlakte-atomen wordt gedefinieerd als:

$$ \text{FE} =\frac{N_{S}}{N_{T}} \cdot 100\% $$ (14)

waar N _S is het aantal oppervlakte-atomen, en N _T is het totale aantal atomen [9]. We kunnen ongelijksoortige clusters vergelijken door de relatieve clustergrootte te definiëren als:

$$ d_{rel} =b(N_{T})^{1/3};~~b =d_{at}^{-1}\cdot \left(\frac{6V_{u}}{\pi n_{u}}\right)^{1/3} $$ (15)

waar d _bij is de covalente atomaire diameter, V _u is het volume van de eenheidscel, en n _u is het aantal atomen in de eenheidscel. De kristalstructuurconstante b is gelijk aan 1.105 voor fcc- en hcp-clusters, 1.137 voor bcc-clusters [1], 1.488 voor eenvoudige kubieke clusters en 1.517 voor diamanten kubieke clusters. Zoals hierboven getoond, is de formule voor FE een verhouding van een kwadratische tot een kubieke voor de clusters en kan worden gemodelleerd door een machtswetcurve fit versus d _rel . De variabele d _rel stelt ons in staat om verschillende clusters met elkaar te vergelijken zonder rekening te houden met de kristalstructuur. Voor sommige Platonische clusters, waar geen kristaleenheidcel is, gebruiken we $N_{T}^{1/3}$ als variabele.

Resultaten en discussie

De studie van de grootte en vorm van metalen nanoclusters is geëvolueerd sinds de kinderschoenen twee decennia geleden. Tabel 20 toont enige relevante vooruitgang vanaf 2018.

In de tabel vermelden we voornamelijk overgangsmetalen, geen legeringen of verbindingen, met uitzondering van de afgeknotte zeshoekige bipyramide, waar alleen Fe₂ O₃ was gevonden. Er is meer synthese van goudclusters geweest dan enig ander element, vanwege zijn eigenschappen en stabiliteit. In de volgende paragrafen beperken we onze bespreking tot specifieke onderwerpen met betrekking tot magische formules en soorten clusters.

FCC-clusters

Acht van de overgangsmetalen kristalliseren in de fcc-structuur, zie tabel 21 hieronder, inclusief de plasmonische edelmetalen en belangrijke katalytisch actieve elementen. De overgrote meerderheid van de synthese van nanoclusters was met deze elementen. Referenties van de synthese van de fcc-elementen met verschillende vormen en maten worden gegeven in Tabel 21.

Legeringen van deze elementen zijn ook van belang, maar referenties hiervan zijn te talrijk om hier te worden vermeld. Vaak zijn de gesynthetiseerde gemeenschappelijke vormen kubussen, octaëders, cuboctaëders en icosaëders. Meestal zijn clusters met (111) facetten gemakkelijker te synthetiseren, aangezien het (111) oppervlak meestal een lagere energie heeft dan het (100) oppervlak [7]. We vinden voor de fcc ruitvormige dodecaëder dat er even en oneven formules bestaan. Deze komen overeen met die in [1], als men de “n . vervangt ” in onze even formules met 2(m −1). De formules voor fcc cuboctahedra in [24] produceren dezelfde magische getallen als de onze, maar zijn met 1 verschoven omdat ze shells nummeren als n =1,2,... en we gebruiken de nummering n =0,1,…. Onze magische formules komen overeen met die in [2, 4], en uit eerbied voor het eerder gepubliceerde werk, en om de continuïteit van de wiskunde te behouden, gebruiken we de [2, 4]-notatie. De 5 fcc-clustervormen en de bijbehorende magische formules verschijnen hieronder.

BCC-clusters

Zeven van de overgangsmetalen in het periodiek systeem hebben de bcc-structuur, zie tabel 21. Van de magnetische elementen Fe, Co en Ni is alleen ijzer bcc. Nanokubussen van ijzer lijken de enige bcc-clustervorm te zijn die tot nu toe is gesynthetiseerd [25]. Hoewel de bulkstructuur van ijzer bcc is, zijn er fcc-nanoclusters gesynthetiseerd [26]. Deze referentie analyseert ook de thermodynamische stabiliteit van de clusters. Hier presenteren we 5 bcc-clustervormen en de bijbehorende magische formules.

HCP-clusters

Twaalf overgangsmetalen hebben de hcp-structuur, zie tabel 21. Veel van deze metalen oxideren echter of hebben geen dwingend wetenschappelijk belang om gesynthetiseerd te worden. Met betrekking tot de hexagonale bipyramidale clustervorm in Tabel 11 zijn gouden clusters gesynthetiseerd [27]. De verwante afgeknotte zeshoekige bipyramide lijkt alleen te zijn gevormd door α −Fe₂ O₃ [28].

Platonische clusters

De Platonische lichamen zijn al bekend sinds de oude Grieken. Ze omvatten de kubus, tetraëder, octaëder, icosaëder en dodecaëder. In eerdere tabellen hebben we magische formules voor fcc- en bcc-kubussen en octaëders vermeld. Hier vermelden we de formules voor de icosaëder, dodecaëder, tetraëder en lichaamsgerichte tetraëder. Zoals eerder vermeld in de sectie "Methoden", is de dodecaëder uniek voor de hier geanalyseerde clusters, in die zin dat c n _s =7 verwijst naar zowel oppervlakte- als bulkatomen. We hebben in figuur 1b laten zien dat de buitenste schil zowel vijfvoudig als zesvoudig gecoördineerde atomen bevat. Wanneer een schil inwendig wordt, worden die vijf- en zesvoudig gecoördineerde atomen zeven- en achtvoudig gecoördineerd met bindingen aan een schil aan weerszijden. Ook zijn de zesvoudig gecoördineerde buitenste schilatomen zevenvoudig gecoördineerd door binding aan de schil binnenin. Er zijn dus zevenvoudige oppervlakte- en bulkgecoördineerde atomen voor de dodecaëder. Elke schaal in de structuur heeft 12 vijfvoudige schaalatomen, die 12n . produceren −12 bulk zevenvoudig gecoördineerde atomen. De rest van de zevenvoudige coördinatie zijn oppervlakte-atomen.

Het is aangetoond dat gouden nanoclusters de platonische vormen aannemen [29]. Deze verwijzing omvat de kubus, tetraëder, octaëder en icosaëder. Later werd ook de gouden dodecaëder nanocluster gesynthetiseerd [30]. Hier laten we zowel de reguliere tetraëder zien, die "fcc-achtig" is in die c _M =12 zoals in fcc-structuren, en de op het lichaam gecentreerde tetraëder in Tabel 16, waar de groene atomen enkelvoudige bindingen hebben. De platonische magische formules worden hieronder weergegeven.

Diamond Cubic, Simple Cubic en Decahedron Clusters

De elementen silicium en germanium hebben het diamant kubisch rooster, evenals de diamantallotroop van koolstof. In het bijzonder waterstof-beëindigd silicium heeft recent belangstelling gekregen. Er is vastgesteld dat het (100) op waterstof eindigende oppervlak, wat leidt tot kubische vormen in clusters, de laagste energie heeft [31]. De synthese van Si-H nanokubussen van 8−15 nm groot is bereikt [32]. Tabel 17 toont een diagram van de op waterstof eindigende Si-H-clusters, met enkelvoudig gebonden waterstofatomen in het groen. Als een nanocluster de kubusvormige diamantvorm aanneemt, zullen er enkele bungelende bindingen zijn, die moeten worden gepassiveerd om de structuur te helpen behouden. Als we naar de magische formules kijken, stellen we voor dat de samenstelling van dergelijke Si-H-clusters is $\phantom {\dot {i}\!}\text {Si}_{8n^{3}+6n^{2}-9n +5}\text {H}_{12n-8}$, waarbij n is het aantal schelpen in het cluster. Dergelijke halfgeleiderkwantumdots kunnen van belang zijn voor optische eigenschappen, en er is vastgesteld dat de variatie in bandafstand met de grootte van clusters met waterstofeindgroepen omgekeerd evenredig is met de clustergrootte [33].

De eenvoudige kubische roosterstructuur is eerder door anderen geanalyseerd [4], hoewel zonder de details die we bieden. We hebben eerder de d . bestudeerd -dimensionale hyperkubusvormen [14]. Polonium is het enige element dat de eenvoudige kubische structuur aanneemt. Het is radioactief, wat kan leiden tot gespecialiseerde toepassingen. Hier presenteren we de magische formules voor diamanten kubieke, eenvoudige en decaëdrische clusters.

Magische topologische formules

Gemeten structurele complexiteit in kristallen kan ons een idee geven van de eenvoud of complexiteit van de structuur en het juiste gebruik kan relevante structuren rangschikken. Voor dergelijke rangschikkingen is het nuttig om rekening te houden met de grafische beschrijving van het kristalrooster, zoals vermeld in de sectie "Methoden". De topologische complexiteit voor kristalstructuren wordt gemeten door de hoekpunt-graadverdeling van de grafiek, I _vd [34], met behulp van de software ToposPro, versie 5.3.2.2 [35]:

$$ I_{vd} =\sum_{i=1}^{v}a_{i} \cdot {\text{log}_{2}}\ {a_{i}} $$ (16)

waar a _ik is de graad (coördinatie) van de i th vertex en sommatie verloopt langs alle v hoekpunten van de quotiëntgrafiek. Deze parameter gebruikt een oneindig kristal in tegenstelling tot de clusters die we hebben overwogen, maar is nuttig om de relatieve complexiteit van verschillende kristalstructuren te meten. Dus hoe hoger het getal of hoe meer informatie in de grafiek, hoe complexer deze is. In Tabel 22 tonen we waarden van I _vd verkregen van ToposPro afgeleid van cif-bestanden voor kristalstructuren in de Crystallographic Open Database. Polonium is het enige element dat kristalliseert in de eenvoudige kubische structuur en de waarde is nul, d.w.z. de quotiëntgrafiek heeft één hoekpunt en nulranden, in overeenstemming met wat we verwachten, dat de eenvoudige kubische structuur inderdaad de minst complexe structuur is. Het zout, NaCl, wordt ook getoond, met twee elementen in de eenvoudige kubische structuur, samen met silicium in de diamantkubische structuur, goud in fcc, ijzer in bcc en kobalt in hcp-structuren. We vermelden dat een andere complexiteitsmaat met betrekking tot de Shannon-entropie [34] niet bruikbaar is omdat deze maat voor alle elementen identiek nul is.

Een vergelijkbare methode als beschreven in de sectie "Methoden" om magische formules te bepalen, kan worden toegepast voor de magische formules die de topologische indices beschrijven. Alleen hier zijn de graden van de polynomen 7, 8 of 9, dus hun waarden voor minstens 10 opeenvolgende n -waarden moeten worden berekend. Dan geeft een interpolatieprobleem van een hogere graad het resultaat. Aangezien het oplossen van een lineair systeem van 10×10 met de symbolische gereedschapskist enige tijd vergt, kunnen alle coëfficiënten voor de topologische indices gelijktijdig worden berekend met behulp van meerdere rechterkanten om de coëfficiënten van alle polynomen te krijgen.

Magische formules voor de topologische indices worden gedetailleerd beschreven in de tabellen 23, 24 en 25. De vier indices die we analyseren, zijn alleen afhankelijk van n , het aantal schelpen in het cluster. Als we naar de resultaten kijken, heeft het eenvoudige kubische rooster als de minst complexe structuur ook de "eenvoudigste" formules. Ondanks onze inspanningen zijn we niet in staat om de Szeged-index van bcc-kubussen op te lossen. Er is geen stabiele oplossing gevonden. Over het algemeen zijn fcc-structuren gemakkelijker op te lossen voor topologische formules. We hebben geen hcp-structuren kunnen oplossen en slechts enkele bcc-structuren. Dit kan te maken hebben met de topologische complexiteit, aangezien het fcc-rooster eenvoudiger is dan het bcc of hcp, zie tabel 22. In de tabellen bieden we formules voor de cuboctaëder, icosaëder en decaëder. We hebben eerder [12] tabellen met numerieke gegevens voor deze indices verstrekt, met het voorbehoud dat de cuboctaëder in [12] verschillende magische getallen had. Hier zien we dat de getabelleerde gegevens beknopt kunnen worden samengevat als magische formules. Ook de graad van de polynoom van de index volgt de regels uit de 3D-ruimte [14]. Sommige topologische indices voor de Platonische lichamen zijn eerder gepubliceerd [36]. Op basis van deze referentie verifiëren we de Wiener-index voor alle vijf vaste stoffen voor n =1. De Wiener-index voor rijen eenheidscellen van het fcc-rooster is bestudeerd [37], maar onze resultaten kunnen niet worden vergeleken omdat we clusters bestuderen.

Verspreiding

Het percentage oppervlakte-atomen (dispersie, FE) van de verschillende clusters wordt weergegeven in figuur 2. Van platina-nanoclusters is bekend dat ze katalytische activiteit hebben met betrekking tot de zuurstofreductiereactie (ORR), die afhankelijk is van grootte en vorm [38]. Deze referentie bepaalde dat platina cuboctaëdrische clusters van 2,2 nm groot maximale ORR-activiteit hadden. Het is ook bekend dat voor PtNi-legeringen het (111) oppervlak de voorkeur heeft voor de ORR [39]. We vergelijken de icosahedrale, octaëdrische, decaëdrische en cuboctaëdrische clusters voor FE op een d _rel =7,5 voor platina bij 2,2 nm. De icosaëdrische, octaëdrische en decaëdrische clusters hebben oppervlakken met (111) vlakken. Met behulp van de machtswetten in Fig. 2 vinden we voor de gegeven d _rel dat de FE voor icosaëdrische clusters 47,9% is, voor cuboctaëdrische 52,8% en voor decaëdrische 57,5% en dat octaëdrische clusters FE=58,9% hebben . Dus, op basis van vorm, hebben de octaëdrische clusters zowel het (111) oppervlak als de hoogste waarde van FE voor een vergelijkbare grootte. Zowel de coëfficiënt van de machtswet als de exponent zijn relevant voor de bepaling van FE voor kleine d _rel . De wiskundige interpretatie van de machtswet-exponent geeft de fysieke betekenis als de relatie van de ordinaat, FE, tot de abscis, d _rel , of de relatieve procentuele verandering van FE naar de relatieve procentuele verandering van d _rel . De machtswet-coëfficiënt is gewoon de waarde van FE wanneer d _rel =1.

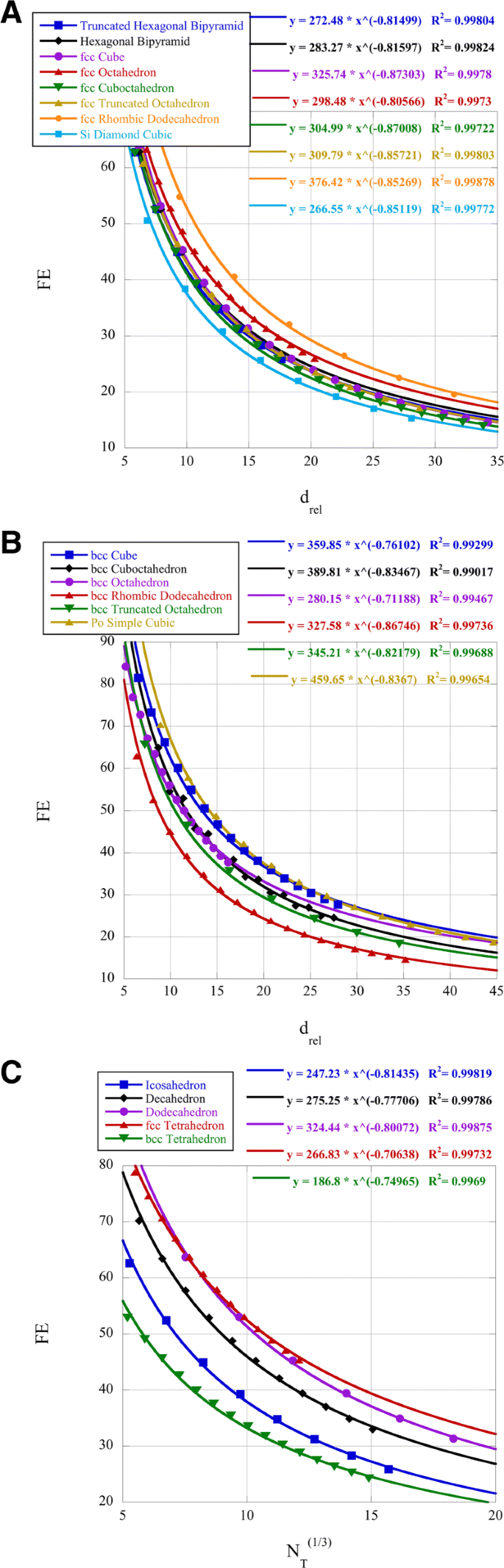
Dispersie FE voor de nanoclusters

Een andere onderzoeksgroep heeft icosaëdrische clusters van platinalegeringen gesynthetiseerd en de activiteit vergeleken met octaëdrische clusters [40]. Deze nanoclusters waren ongeveer 13 nm groot of N =20.000 voor octaëdrische clusters en N =15.000 voor icosaëdrische clusters. Dit levert een d . op _rel =30 voor de octaëdrische clusters en 25 voor de icosahedrale. Met behulp van de relevante machtswetten geeft dit FE=18.0% voor de octaëdrische en 19,8% voor de icosaëdrische clusters. Er is heel weinig verschil in FE voor deze grootte van het cluster, maar het icosahedrale cluster heeft een aanzienlijke hoeveelheid spanning als gevolg van twinning, wat het centrum van de d-band kan verschuiven, waardoor de ORR-resultaten worden beïnvloed [40]. Gezien de grootte-afhankelijke gegevens van [38], kan echter worden gesuggereerd dat kleinere clusters nog hogere ORR-gegevens zouden produceren. Inderdaad, 4 nm Pt₃ Ni-octaëders hebben, wanneer ze zijn gedoteerd met Mo, recordhoge ORR-resultaten opgeleverd [41].

Conclusies

We hebben 19 soorten nanoclusters bestudeerd en enkele relevante magische formules voor het aantal atomen, bindingen, coördinatiegetallen en topologische indices. Deze omvatten de fcc, bcc, hcp, de platonische lichamen, diamant kubische, eenvoudige kubieke en decaëdrische clusters. De meeste van deze resultaten zijn gedetailleerder dan eerder bepaald, en een groot aantal wordt voor het eerst opgesomd. Een groot doel van materiaalgerelateerd onderzoek is de correlatie van structuur met eigenschappen. Deze gedetailleerde studie van de magische relaties voor nanoclusters is een stap in die richting. Een voorbeeld is de bespreking van de dispersie van oppervlakte-atomen en de relatie met de katalytische activiteit. Het is onze bedoeling dat deze resultaten wetenschappers zullen helpen bij hun onderzoek naar de structuur van nanoclusters en de bijbehorende eigenschappen.

Afkortingen

bcc:: lichaamsgecentreerd kubisch
cif:: kristallografisch informatiebestand
fcc:: op het gezicht gecentreerd kubisch
FE:: Blootgestelde fractie, dispersie
hcp:: zeshoekig dicht verpakt
ORR:: Oxidatiereductiereactie
rW(G):: Omgekeerde Wiener Index
Sz(G):: Szeged-index
W(G):: Wiener-index
WW(G):: Hyper-Wiener-index

ZnO poreuze nanoplaten met gedeeltelijke oppervlaktemodificatie voor verbeterde ladingsscheiding en hoge fotokatalytische activiteit onder zonnestraling Effecten van meshed p-type contactstructuur op het lichtextractie-effect voor Deep Ultraviolet Flip-Chip Light-Emitting Diodes

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal