Eigenschappen van de geometrische fase in elektromechanische oscillaties van op koolstof-nanobuisjes gebaseerde nanodraadresonatoren

Abstract

De geometrische fase is een extra fase-evolutie in de golffunctie van trillingen die potentieel toepasbaar is in een breed scala van wetenschap en technologie. De kenmerken van de geometrische fase in de geperste toestand voor een op koolstof-nanobuis gebaseerde nanodraadresonator zijn onderzocht met behulp van de invariante operatormethode. De introductie van een lineaire invariante operator, die nuttig is voor het behandelen van een gecompliceerd tijdsafhankelijk Hamiltoniaans systeem, stelde ons in staat om de analytische formule van de geometrische fase af te leiden. Door hiervan gebruik te maken, hebben we het tijdsgedrag van de geometrische fase geanalyseerd op basis van relevante illustraties. De invloed van knijpparameters op de evolutie van de geometrische fase is onderzocht. De geometrische fase, in het algemeen, oscilleert en de omhullende van een dergelijke oscillatie neemt in de loop van de tijd toe. De snelheid van de toename van de geometrische fase is groot wanneer de parameters, zoals de klassieke amplitude van de oscillatie, de dempingsfactor en de amplitude van de drijvende kracht, groot zijn. We hebben een zeer sterke toename van de geometrische fase in de tijd bevestigd in het geval dat de hoekfrequentie van het systeem de resonantiehoekfrequentie nadert. Onze ontwikkeling met betrekking tot de kenmerken van de geometrische fase is cruciaal voor het begrijpen van de topologische kenmerken in nanodraadoscillaties.

Inleiding

Mechanische trillingen van de kleinste resonatoren, zoals op koolstof-nanobuis gebaseerde (CNT-gebaseerde) nanodraden [1-3], halfgeleidende nanodraden [4], grafenen [5] en zwevende deeltjes [6], zijn een belangrijk onderzoeksonderwerp geweest in de nanowetenschapsgemeenschap voor meer dan een decennium. Actieve onderzoeken met betrekking tot elektromechanische oscillaties van nanodraadresonatoren aangedreven door een externe periodieke kracht zijn uitgevoerd in zowel theoretische als experimentele sferen. In het bijzonder hebben op CNT gebaseerde nanodraadresonatoren aanzienlijke belangstelling gewekt als mechanische apparaten op nanoschaal vanwege hun buitengewone gevoeligheden met hoogwaardige factoren voor een kleine verstoring van de omgeving. Opgeschorte CNT-gebaseerde nanodraadresonatoren zijn veelbelovende kandidaten voor apparaten die een breed scala aan fysieke grootheden meten, zoals EM-golven [2], kleine krachten [7], massa's [8], temperaturen [9] en geluiden [10].

Analyses van de kwantitatieve fase-evolutie in nanodraadoscillaties zijn vereist om de onderliggende kenmerken van het systeem theoretisch op te helderen. Met betrekking tot de kwantumtrillingstoestanden van de op CNT gebaseerde nanodraadresonatoren [11], komt zowel de geometrische fase [12] als de gebruikelijke dynamische fase naar voren als een aanvullende evolutie van de fase. De geometrische fase [12] is een anholonomische vorm van een kwantumtoestand die toepasbaar kan zijn op diverse gebieden van de natuurkunde. Analyses van de geometrische fase kunnen mogelijk worden toegepast bij het karakteriseren van nano-eigenschappen van nanodraden, zoals de resonantieprofielen [13, 14], sterke kwantumtrillingen [15, 16], spanningsrelaxatiemechanismen [17, 18], de opkomst van Dirac-magnetoplasmonen [19], en de topologie van Aharonov-Bohm-oscillaties [20].

De studie van de geometrische fase geassocieerd met niet-adiabatische dynamica kan inzicht verschaffen in nanomechanische systemen, wat nodig is voor de vooruitgang van nauwkeurige simulatietechnieken [21]. De voorbereiding, manipulatie en detectie van kwantumtoestanden zijn belangrijke factoren in kwantumtechnologieën. Het doel van dit onderzoek is om licht te werpen op het tijdsgedrag van de geometrische fase die plaatsvindt in kwantumtoestanden van nanodraadoscillaties. Om het mechanisme van op CNT gebaseerde nanodraadtrillingen te begrijpen, zullen we de tijdsevolutie van de geometrische fase in de samengedrukte toestand onderzoeken, wat een klassiek-achtige kwantumtoestand is zoals de coherente toestand. De verdienste van de geperste toestand is dat de onzekerheid van een kwadratuur in die toestand aanzienlijk kan worden verminderd ten koste van de toename van de onzekerheid van de andere kwadratuur, terwijl een dergelijke onzekerheidsmodulatie onmogelijk is in de coherente toestand. In het bijzonder zullen we de effecten van resonantie op de geometrische fase analyseren. Omdat de resonantie-energie significant verschilt van de energie van de niet-resonante toestand [22, 23], is het topologische gedrag van de golffunctie niet triviaal en kan het aanzienlijk afwijken van dat in normale situaties. De invloed van de verandering van fysische parameters en de knijpparameters op de evolutie van de geometrische fase zal ook rigoureus worden geanalyseerd. De geometrische fasen zijn alomtegenwoordig in dynamische systemen [24] en kunnen worden toegepast op verschillende moderne technologieën, zoals kwantumberekening [25], intensiteitsinterferometrieën [26], fotonische multitasking [27], kwantumdetectieprotocollen [28] en golf -stabiliteitsmetingen [29].

De Hamiltoniaan van het systeem omvat tijdfuncties die verband houden met de demping van het systeem en de externe drijvende kracht. Het systeem is dus een soort tijdsafhankelijke Hamiltoniaanse systemen (TDHS's) waarvan tot voor kort de kwantummechanische problemen uitgebreid werden bestudeerd. De tijdfunctie in de Hamiltoniaan van een TDHS kan in de meeste gevallen niet worden gescheiden van de functie van canonieke variabelen, waardoor de conventionele methode voor het scheiden van variabelen voor het oplossen van de Schrödinger-vergelijking niet beschikbaar is. Een alternatieve krachtige methode die is ontwikkeld om deze moeilijkheid te overwinnen, is de invariante operatormethode die is geïntroduceerd door Lewis en Riesenfeld [30, 31]. Deze methode is een zeer nuttig wiskundig hulpmiddel bij het afleiden van kwantumoplossingen van een TDHS. Veel kwantummechanische problemen beschreven door TDHS's worden op basis van deze methode onderzocht. Ze omvatten bijvoorbeeld chaotische deeltjesverstrooiing [32], lichtvoortplanting in in de tijd variërende media [33], controle van ingesloten aangedreven elektronen [34] en niet-klassieke kwantum-nano-elektronische circuits [35]. Er is een verscheidenheid aan andere methoden voor kwantummechanische behandelingen van TDHS's, waaronder unitaire transformatiemethode [36], Lie algebraïsche methode [37] en Hamiltoniaanse schattingsmethode [38].

Aangezien het systeem een TDHS is, gebruiken we de invariante operatormethode om kwantumoplossingen van het systeem te verkrijgen. Er wordt een lineaire invariante operator geïntroduceerd die wordt weergegeven in termen van de annihilatie-operator. Terwijl de annihilatie- en de creatie-operatoren worden weergegeven in termen van tijd vanwege de tijdsafhankelijkheid van het systeem, kunnen zowel de coherente als de geperste toestanden worden verkregen met behulp van deze ladderoperators. De geometrische fase van het systeem zal analytisch worden geëvalueerd door gebruik te maken van de golffunctie in de geperste toestand. De tijdsevolutie van de geometrische fase zal in detail worden geanalyseerd op basis van de afbeeldingen die worden weergegeven met diverse keuzes van parameters.

Methoden

Om de geometrische fase te onderzoeken, moeten we eerst de klassieke bewegingsvergelijking van de nanodraadtip opstellen. Omdat de geometrische fase verschijnt in de kwantumgolfevolutie van een TDHS, is het noodzakelijk om golffuncties af te leiden in een specifieke kwantumtoestand die we beheren. We zullen de samengedrukte toestand beschouwen zoals vermeld in het inleidende deel. De golffuncties in de diverse kwantumtoestanden van een TDHS, inclusief de samengedrukte toestand, kunnen worden verkregen met de invariante operatormethode.

De bewegingsvergelijking voor de tijdsafhankelijke amplitude x voor een buigmodus van een gesuspendeerde koolstofnanobuis met een effectieve massa m wordt gegeven door [1]

$$ \ddot{x}+\left(\frac{\omega_{0}}{Q} +\eta x^{2}\right) \dot{x}+\left(\omega_{0}^{ 2}+\beta x^{2}\right) x =f_{\mathrm{d}}\cos (\omega t), $$ (1)

waar ω ₀ is de resonantiehoekfrequentie, Q de kwaliteitsfactor, f _d de elektrostatische aandrijfkracht gedeeld door m , η de niet-lineaire dempingscoëfficiënt, en β de Duffing-parameter. Laten we voor het gemak aannemen dat de verplaatsing van de punt voldoende klein is ten opzichte van de lengte van de CNT-draad. Dan kunnen we de niet-lineaire termen in Vgl. (1), leidend tot [2]

$$ \ddot{x}+\frac{\omega_{0}}{Q} \dot{x}+\omega_{0}^{2} x =f_{\mathrm{d}}\cos (\omega t). $$ (2)

De Hamiltoniaan van het systeem dat Vgl. (2) wordt gegeven door

$$ \hat{H}=e^{-\gamma t} \frac{\hat{p}^{2}}{2m} +\frac{1}{2}me^{\gamma t} \left [\omega_{0}^{2} \hat{x}^{2} - 2f_{\mathrm{d}}\cos (\omega t)\hat{x}\right], $$ (3)

waar γ =ω ₀ /Q . De klassieke oplossing van Vgl. (2) bestaat uit een complementaire functie X _c (t ) en een bepaalde oplossing X _p (t ), die worden gegeven door

$$\begin{array}{@{}rcl@{}} &&X_{c}(t)=X_{c,0}e^{-\gamma t/2}\cos(\Omega t+\varphi) , \end{array} $$ (4) $$\begin{array}{@{}rcl@{}} &&X_{p}(t) =X_{p,0}\cos (\omega t - \ delta), \end{array} $$ (5)

waar X _{c ,0} is een constante, $\Omega =\sqrt {\omega _{0}^{2} - \gamma ^{2}/4}$, φ is een willekeurige fase, en

$$\begin{array}{@{}rcl@{}} X_{p,0}&=&\frac{f_{\mathrm{d}}}{\sqrt{\left(\omega_{0}^ {2} -\omega^{2}\right)^{2} + \gamma^{2} \omega^{2}}}, \end{array} $$ (6) $$\begin{array} {@{}rcl@{}} \delta &=&\tan^{-1} \frac{\gamma \omega}{ \omega_{0}^{2} -\omega^{2}}. \end{array} $$ (7)

De klassieke oplossing in de impulsruimte wordt op een vergelijkbare manier gegeven, waarbij de complementaire functie $P_{c} (t) =me^{\gamma t} \dot {X}_{c}(t)$ is en de specifieke oplossing is $P_{p} (t) =ik^{\gamma t} \dot {X}_{p}(t)$. Om de geometrische fase van het systeem te onderzoeken, moeten we eerst kwantumoplossingen afleiden. Merk op dat de Hamiltoniaan van het systeem gegeven in Vgl. (3) is expliciet tijdsafhankelijk. Om kwantumoplossingen van het systeem af te leiden, gebruiken we de invariante operatormethode [30, 31], wat een nuttige methode is wanneer we zo'n tijdvariërend systeem behandelen. Een invariante operator $\hat {I}$ van het systeem kan worden afgeleid uit de Liouville-von Neumann-vergelijking, die wordt gegeven door ${d \hat {I}}/{dt} ={\partial \hat {I}}/{\partial t} + \left [\hat {I},\hat {H}\right ]/\left (i\hbar \right) =0$. Vandaar dat uit een rigoureuze evaluatie na het invoegen van Vgl. (3) in deze vergelijking hebben we een lineaire invariante operator [34] van de vorm

$$ \hat{I} =\hat{A} e^{i\Omega t}, $$ (8)

waarbij $\hat {A}$ de annihilatie-operator is die wordt gegeven door

$$ \begin{aligned} \hat{A} =&\left(2\hbar m\Omega\right)^{-1/2} \left[ m \left(\Omega+ i\frac{\gamma}{ 2} \right) e^{\gamma t/2}\left[\hat{x}-X_{p}(t)\right]\right.\\ &\left.+ie^{-\gamma t /2} \left[\hat{p}-P_{p}(t)\right]\! {\vphantom{\left(\Omega+ i\frac{\gamma}{2} \right)}}\right]. \end{uitgelijnd} $$ (9)

De hermitische adjunct van Vgl. (9), $\hat {A}^{\dagger }$, is de aanmaakoperator.

We kunnen de eigenwaardevergelijking van $\hat {A}$ uitdrukken als

$$ \hat{A} |A \rangle =A |A \rangle. $$ (10)

Door de bovenstaande vergelijking te evalueren, hebben we de uitdrukking van de eigenwaarde zodanig dat

$$ A(t) =A(0) e^{-i\Omega t}, $$ (11)

waar A (0)=A ₀ e ^{−ik φ} met

$$ A_{0} =\left[m\Omega/(2\hbar)\right]^{1/2}X_{c,0}. $$ (12)

Terwijl de coherente toestand |A 〉 is de eigentoestand van $\hat {A}$, de samengedrukte toestand is de eigentoestand van een operator $\hat {B}$ die wordt gegeven door

$$ \hat{B} =\mu \hat{A} + \nu \hat{A}^{\dolk}, $$ (13)

waar μ en ν zijn complexe variabelen die de vergelijking opleveren

$$ |\mu|^{2} - |\nu|^{2} =1. $$ (14)

Als we de eigenwaardevergelijking van $\hat {B}$ schrijven in de vorm

$$ \hat{B} |B \rangle =B |B \rangle, $$ (15)

|B 〉 is de geperste toestand. Door deze vergelijking in de configuratieruimte op te lossen, krijgen we

$$ {\begin{aligned} \langle {x}|B\rangle =&^{4}\!\!\!\sqrt{\frac{m \Omega e^{\gamma t}}{\hbar\ pi(\mu-\nu)(\mu^{*}-\nu^{*})}} \exp \left\{- \frac{1}{\hbar (\mu-\nu)} \left [\frac{1}{2} me^{\gamma t}\left({\vphantom{\frac{1}{2}}}(\mu+\nu)\Omega \right.\right.\right. \\ &\links +\frac{i\gamma}{2}(\mu-\nu)\right)\left[x-X_{p}(t)\right]^{2} -[iP_{ p}(t)(\mu-\nu)+ \left(2\hbar m \Omega e^{\gamma t}\right)^{1/2} \\ &\left. \left.\times(\mu A+\nu A^{*}) ]\left[x-X_{p}(t)\right] {\vphantom{\frac{1}{2} me^{\gamma t}}}\right]-\frac{|A|^{2}+A^{2}}{2(\mu-\nu)(\mu^{*}-\nu^{*})} \Rechtsaf\}. \end{uitgelijnd}} $$ (16)

De golffunctie in de geperste toestand is dus afgeleid zoals gegeven in Vgl. (16). Kwantumkenmerken van het systeem kunnen worden verduidelijkt op basis van een dergelijke analytische beschrijving van de golffunctie. Voor μ =1 en ν =0, vgl. (16) reduceert tot de golffunctie in de coherente toestand, wat de eigentoestand is van Vgl. (10) in de configuratieruimte. De golffunctie, Vgl. (16), zal in de volgende sectie worden gebruikt om de geometrische fase in de samengedrukte toestand af te leiden.

Resultaten en discussie

Het is algemeen bekend dat de fase in de evolutie van kwantumgolven zowel de geometrische fase als de dynamische fase omvat. De geometrische fase werd voor het eerst ontdekt door Berry in 1984 [12] voor een systeem dat cyclisch evolueert met een adiabatische verandering. Volgens de adiabatische stelling in de kwantummechanica zal een ogenblikkelijke eigentoestand van een kwantumtoestand in een cyclische evolutie in de parameterruimte later in dezelfde toestand blijven, terwijl er een extra accumulatie is van de kwantumfase die de Berry-fase is. Een veralgemening van de Berry-fase op een manier die niet-adiabatische, niet-cyclische en/of niet-unitaire evolutie van het kwantumsysteem omvat, is de geometrische fase.

De geometrische fase in samengedrukte toestand wordt gegeven door

$$ \gamma_{G}(t) =\int_{0}^{t} \langle B(t') |i\frac{\partial}{\partial t'}| B(t') \rangle dt' +\gamma_{G}(0). $$ (17)

De differentiatie van de golffunctie met betrekking tot tijd in configuratieruimte wordt

$$ \frac{\partial \langle {x}|B\rangle}{\partial t} \,=\, \left\{ f_{1}(t) \!\left[x-X_{p}( t)\right]^{2}\,+\,f_{2}(t) \left[x\,-\,X_{p}(t)\right]\,+\,f_{3}( t) \rechts\}\! \!\langle {x}|B\rangle, $$ (18)

waar

$$ f_{1}(t) =- \frac{m\gamma e^{\gamma t}}{2\hbar (\mu-\nu)} \left((\mu+\nu)\Omega + \ frac{i\gamma}{2}(\mu-\nu) \right), $$ (19) $$ {\begin{aligned} f_{2}(t) &=\frac{1}{\hbar (\mu-\nu)}\left[ \left((\mu+\nu)\Omega + \frac{i\gamma}{2}(\mu-\nu) \right) P_{p}(t) -ime^{\gamma t} \right.\\ &\quad\times\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\ omega t)\right](\mu-\nu) +\left(2\hbar m \Omega e^{\gamma t}\right)^{1/2} \\ &\quad \left.\times\ left(\frac{\gamma}{2}\left(\mu A + \nu A^{*}\right)-i\Omega \left(\mu A - \nu A^{*}\right) \ rechts) \rechts], \\ \end{uitgelijnd}} $$ (20) $$ {\begin{uitgelijnd} f_{3}(t) &\!=\frac{\gamma}{4}-\frac {1}{\hbar me^{\gamma t}(\mu-\nu)} \left[iP_{p}(t)(\mu-\nu) + \left(2\hbar m\Omega e^ {\gamma t}\right)^{1/2} \right.\\ &\quad\left.\times\left(\mu A+\nu A^{*}\right){\vphantom{\left( 2\hbar m\Omega e^{\gamma t}\right)^{1/2}}}\right] P_{p}(t)+ \frac{i\Omega A^{2}}{(\ mu-\nu)\left(\mu^{*}-\nu^{*}\right)}. \end{uitgelijnd}} $$ (21)

Verdere evaluatie na het invoegen van Eq. (18) in Vgl. (17) geeft

$$ {\begin{aligned} \gamma_{G}(t) =&\int_{0}^{t} dt' \left[ A_{0}^{2}\left(\frac{\gamma^{ 2}}{4\Omega}+\Omega + g_{1} \sin\left[2\left(\Omega t'+\varphi\right)\right] +g_{2} \cos\left[2\ left(\Omega t'+\varphi\right)\right] \right) \right.\\ &\left.-A_{0}\left[ g_{3}(t') \sin\left(\Omega t'+\varphi\right) +g_{4}(t') \cos\left(\Omega t'+\varphi\right) \right]+ g_{5}(t') {\vphantom{\frac {\gamma^{2}}{4\Omega}}}\right] +\gamma_{G}(0), \end{aligned}} $$ (22)

waar

$$\begin{array}{*{20}l} g_{1}~ &=\frac{\gamma}{2} + \frac{i\Omega \left(\mu\nu^{*}-\ mu^{*}\nu\right)}{(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)}, \end{array} $$ (23) $$\begin{array}{*{20}l} g_{2}~ &=\frac{\gamma^{2}}{4\Omega}+\Omega\frac{2|\nu|^{2 }- \left(\mu\nu^{*}+\mu^{*}\nu\right)}{(\mu-\nu) \left(\mu^{*}-\nu^{*} \right)}, \end{array} $$ (24) $$\begin{array}{*{20}l} g_{3}(t) &=\left(\frac{2\Omega}{m \hbar e^{\gamma t}} \right)^{1/2}P_{p}(t), \end{array} $$ (25) $$ {\begin{aligned} g_{4}( t) =\frac{1}{\sqrt{2\hbar\Omega}}\left(\frac{\gamma }{\sqrt{me^{\gamma t}}}P_{p}(t) - 2 \sqrt{me^{\gamma t}}\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\omega t)\right]\ rechts), \end{aligned}} $$ (26) $$ {\begin{aligned} g_{5}(t) &=\frac{P_{p}^{2}(t)}{\hbar mij ^{\gamma t}}+\frac{\gamma^{2}}{8\Omega}\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\ nu^{*}\right) +1\right] \\ &\quad +\frac{i\gamma}{4(\mu-\nu)\left(\mu^{*}-\nu^{* }\right)} \left[|\mu|^{2}\left(\nu^{2}-\nu^{*2}\right)-|\nu|^{2}\lef t(\mu^{2}-\mu^{*2}\right)\right.\\ &\quad\left.+ (2|\nu|^{2}+1)\left(\mu\ nu^{*}-\mu^{*}\nu\right) +(\mu-\mu^{*})(\nu-\nu^{*})\right]. \end{uitgelijnd}} $$ (27)

De laatste term in g ₅ dat bevat (μ −μ ^∗ )(ν −ν ^∗ ) is als fase ontoereikend omdat dit een puur denkbeeldig getal is. Daarom verwijderen we deze term nu door ten minste een van μ . te kiezen en ν als een reële waarde. Deze remedie kan altijd worden gedaan zonder verlies van algemeenheid, omdat alleen de relatieve fase tussen μ en ν heeft een fysieke betekenis in plaats van hun absolute fasen.

Vanaf de uitvoering van de integratie in Vgl. (22) we hebben

$$ {\begin{aligned} \gamma_{G}(t) &=A_{0}^{2}\left[\left(\frac{\gamma^{2}}{4\Omega}+\Omega \right)t + \frac{g_{1}}{\Omega}\sin(\Omega t+2\varphi) \sin(\Omega t) +\frac{g_{2}}{\Omega} \cos (\Omega t+2\varphi) \right.\\ &\quad\left.\times\sin(\Omega t) {\vphantom{\frac{\gamma^{2}}{4\Omega}}} \right]\!-A_{0}\left[ \left(\frac{2m\Omega}{\hbar} \right)^{1/2}\omega X_{p,0} \bar{g}_ {3}(t) +\sqrt{\frac{2m}{\hbar\Omega}}\frac{1}{4\omega^{2}+\gamma^{2}}\bar{g}_{ 4}(t) \right]\\ &\quad+ \bar{g}_{5}(t) +\gamma_{G}(0), \end{aligned}} $$ (28)

waarbij $\bar {g}_{i}(t)~(i=3,4,5)$ wordt gegeven door

$$ \bar{g}_{i}(t) =G_{i}(t) -G_{i}(0), $$ (29)

met

$$ {\begin{aligned} G_{3}(\tau) &=e^{\gamma \tau/2}\left(\frac{1}{4(\Omega+\omega)^{2}+\ gamma^{2}} \left\{2(\Omega+\omega)\sin[(\Omega+\omega)\tau+\varphi-\delta] \right.\right.\\ &\quad\left.+\ gamma \cos[(\Omega+\omega)\tau+\varphi-\delta] \right\}- \frac{1}{4(\Omega-\omega)^{2}+\gamma^{2}} \ { 2(\Omega-\omega) \\ &\quad\left.\left.\times\sin[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\ !+\gamma \cos[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\right\} {\vphantom{\frac{1}{4(\Omega+\ omega)^{2}+\gamma^{2}}}}\right),\\ \end{aligned}} $$ (30) $$ {\begin{aligned} G_{4}(\tau) &=e^{\gamma \tau/2} \left\{X_{p,0} \left\{ \gamma\omega[ 2\omega\cos(\omega \tau-\delta)-\gamma \sin( \omega \tau-\delta)] -2\omega_{0}^{2} \right.\right.\\ &\quad\left.\times[2\omega\sin(\omega \tau-\delta )+\gamma \cos(\omega \tau-\delta)] {\vphantom{X_{p,0}}}\right\}+2f_{\mathrm{d}} [ 2\omega\sin(\omega \tau) \\ &\left.\left.\quad+\gamma \cos(\omega \tau)\right]{\vphantom{X_{p,0}}}\right\}, \\ \end{uitgelijnd }} $$ ( 31) $$ {\begin{aligned} G_{5}(\tau) &=\frac{m\omega^{2}}{2\hbar}X_{p,0}^{2} \frac{e ^{\gamma \tau}}{\gamma \left(4\omega^{2}+\gamma^{2}\right)} \left\{ \gamma^{2}+4\omega^{2} -\gamma^{2} \cos[2(\omega\tau -\delta)]\right.\\ &\quad\left.-2\gamma\omega \sin[2(\omega \tau -\delta )] {\vphantom{\gamma^{2}+4\omega^{2} -\gamma^{2}}}\right\} +\frac{\gamma^{2} \tau}{8\Omega }\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\nu^{*}\right)+1\right] \\ &\quad+\frac{i \gamma \tau}{4(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)} \left[|\mu|^{2}\left(\nu ^{2}-\nu^{*2}\right)-|\nu|^{2}\left(\mu^{2}-\mu^{*2}\right)\right.\\ &\quad\left.+\left(2|\nu|^{2}+1\right)\left(\mu\nu^{*}-\mu^{*}\nu\right)\right]. \end{uitgelijnd}} $$ (32)

We hebben dus de volledige geometrische fase geëvalueerd in de geperste toestand, die wordt gegeven door Vgl. (28) met vergelijkingen. (23), (24) en (29)–(32).

De tijdsevolutie van de geometrische fase is geïllustreerd in Fig. 1, 2, 3 en 4. Uit figuur 1 zien we dat de geometrische fase oscilleert en dat de omhullende van een dergelijke oscillatie in de loop van de tijd toeneemt. De toename van de envelop is groter wanneer A ₀ is groot. Het patroon van de oscillatie wordt geleidelijk onregelmatig naarmate de waarden van μ en ν toenemen. Bovendien wordt de amplitude van de oscillatie groter naarmate de tijd verstrijkt.

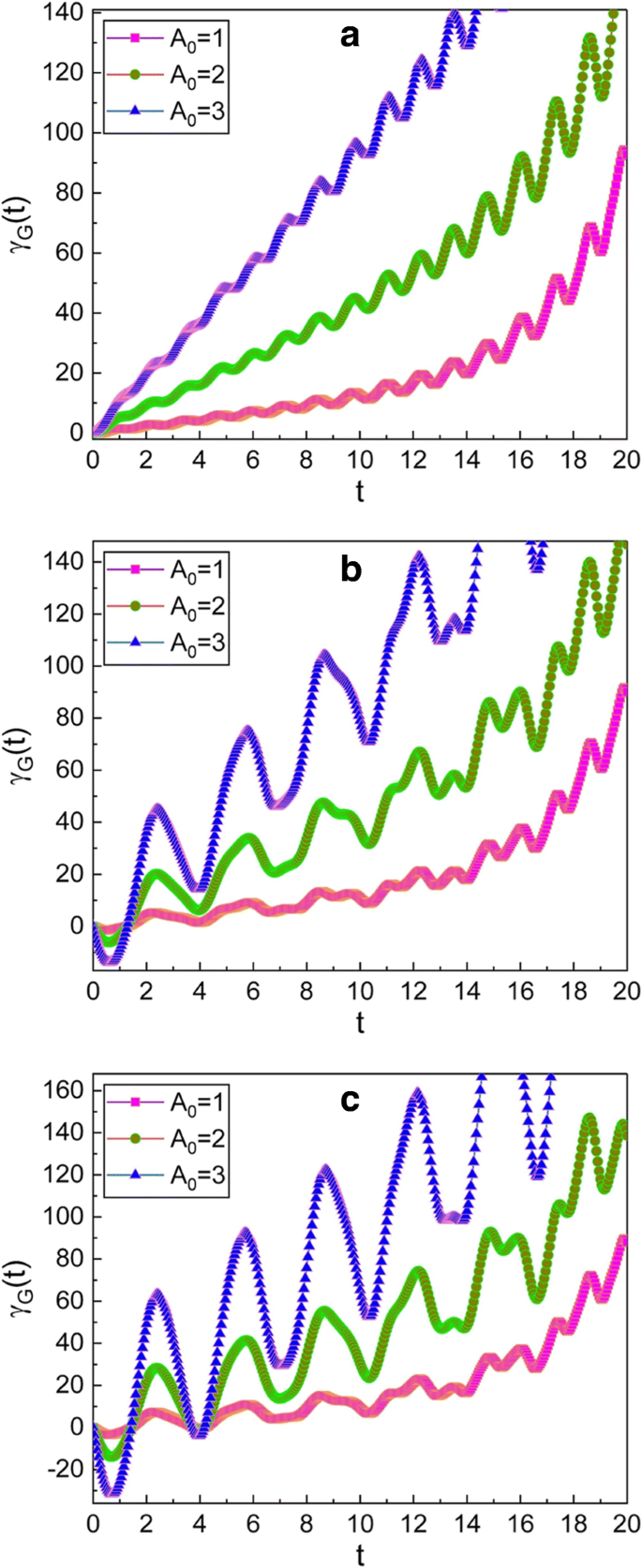
Tijdsevolutie van de geometrische fase voor verschillende waarden van A ₀ . De waarden van (μ , ν ) die in de afbeeldingen worden gebruikt, zijn (1, 0) voor a , ($\sqrt {2}$, 1) voor b , en ($\sqrt {3}$, $\sqrt {2}$) voor c . We hebben m . gebruikt =1, ω ₀ =1, ω =5, γ =0,35, f _d =1, $\hbar =1$, φ =0, en γ _G (0)=0. De fase en alle parameters worden gemakshalve als dimensieloos beschouwd en deze conventie zal ook worden toegepast op de volgende figuren. Omdat A ₀ wordt gegeven in termen van de klassieke amplitude X _{c ,0} van de complementaire functie [zie Vgl. (12)], kunnen we uit de grafieken bevestigen dat de geometrische fase groot is wanneer de oscillatie-amplitude hoog is. We zien ook dat de fluctuatie van γ _G (t ) wordt groot naarmate de waarden μ en ν toenemen onder de voorwaarde gegeven in Vgl. (14)

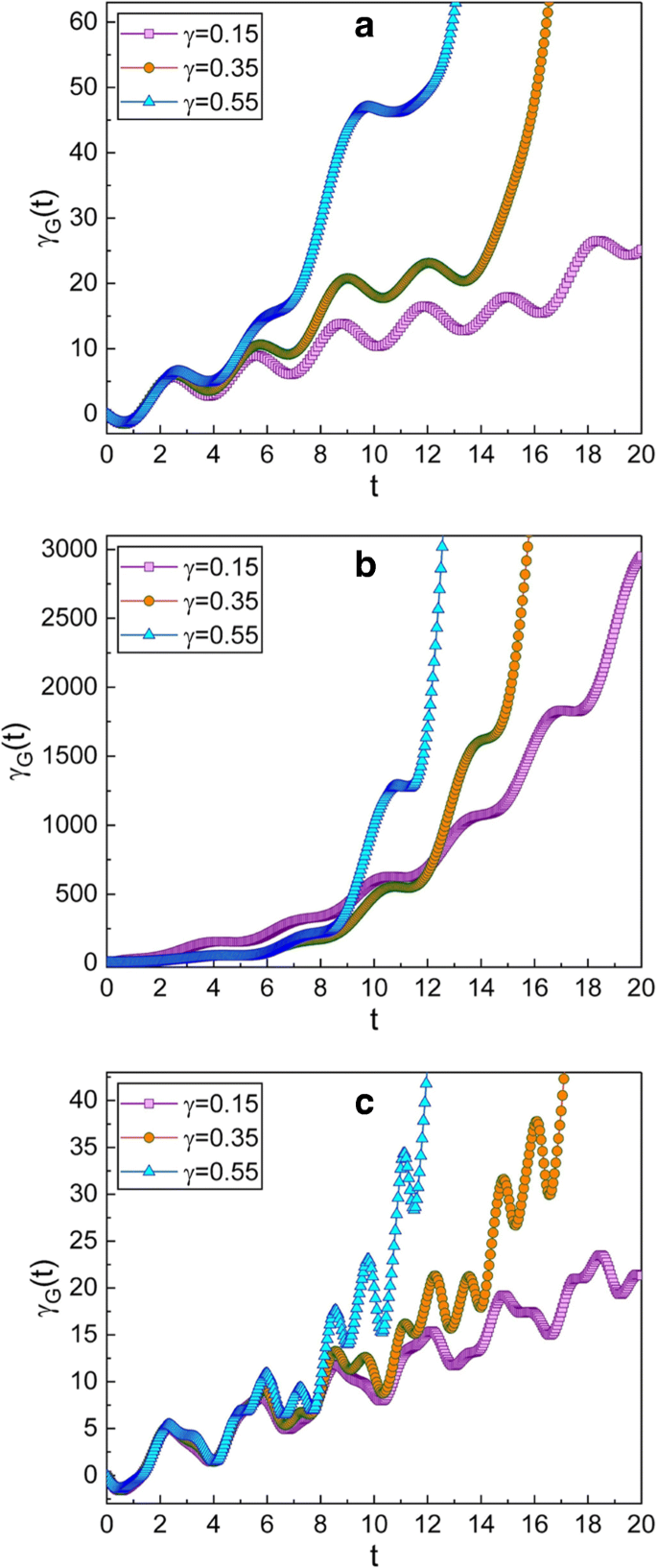
Tijdsevolutie van de geometrische fase voor verschillende waarden van γ . De waarde van ω gebruikt in de afbeeldingen is 0,3 voor a , 0,99 voor b , en 5 voor c . De hier gekozen knijpparameters zijn $\mu =\sqrt {2}$ en ν =1; deze keuze geeft q -squeezed staat op de eerste keer. Andere hoeveelheden die we hebben gebruikt zijn m =1, ω ₀ =1, A ₀ =1, f _d =1, $\hbar =1$, φ =0, en γ _G (0)=0. We bevestigen dat de geometrische fase groot is wanneer de dempingsfactor γ is in de meeste gevallen groot, maar niet allemaal. De frequentie van de zaak b ligt dicht bij de resonantiefrequentie, terwijl die van a en c zijn verre van de resonerende. De geometrische fase voor het resonerende geval (b ) neemt in de loop van de tijd zeer snel toe

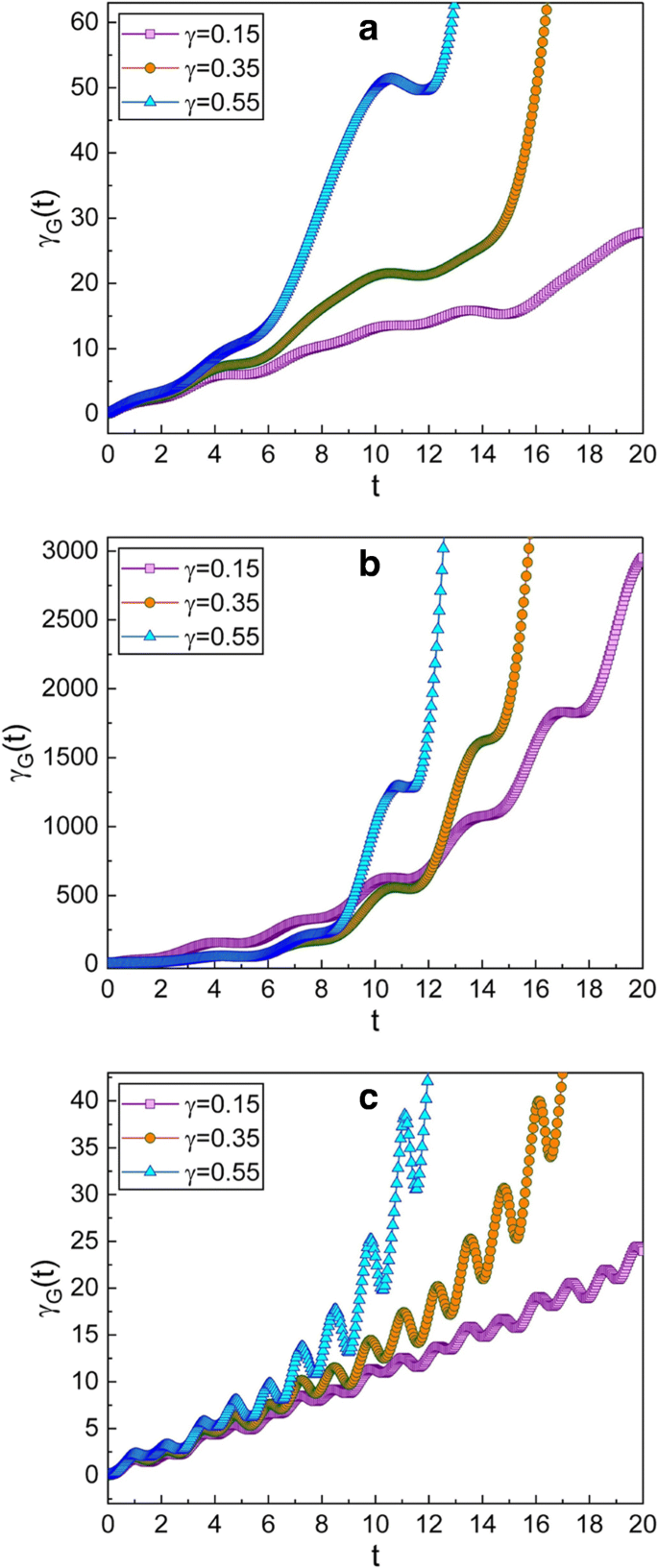
een –c Deze afbeelding is hetzelfde als in Fig. 2, maar voor het geval dat de gekozen knijpparameters $\mu =\sqrt {2}$ en ν zijn =−1 die een p . geeft -squeezed staat op de eerste keer. Uit het feit dat de algemene grafische weergave in dit geval niet zo veel verschilt van de overeenkomstige afbeeldingen van Fig. 2, kunnen we bevestigen dat de evolutie van γ _G (t ) is bijna niet relevant voor de soorten knijpen, zolang de absolute waarden van μ en ν niet veranderen

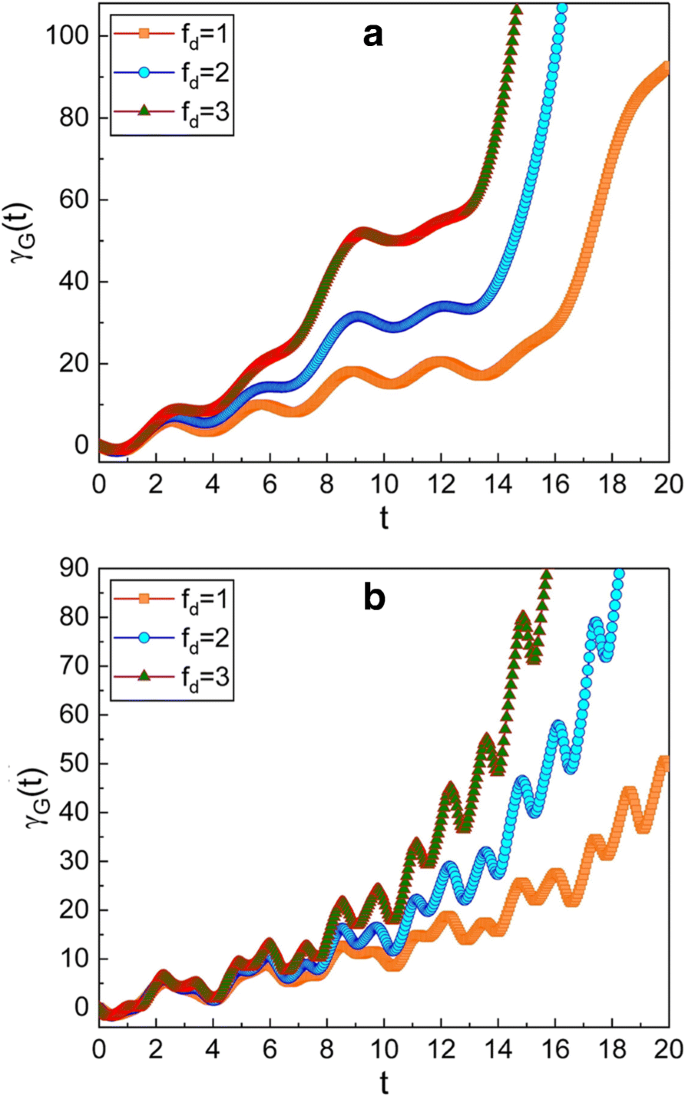
Tijdsevolutie van de geometrische fase voor verschillende waarden van f _d . De waarde van ω gebruikt in de afbeeldingen is 0,3 voor a en 5 voor b . We hebben gebruik gemaakt van $\mu =\sqrt {2}$, ν =1, m =1, ω ₀ =1, γ =0.3, A ₀ =1, $\hbar =1$, φ =0, en γ _G (0)=0. Aangezien de amplitude (f _d ) van de drijvende kracht toeneemt, wordt de geometrische fase groot

De knijpeffecten in de samengeperste toestand zijn afhankelijk van de knijpparameter c waar c =μ /ν is onderzocht in ref. [39]. Volgens de analyse gegeven in ref. [39] (zie Fig. 1(a) in ref. [39]), de samengedrukte toestand geïllustreerd in Fig. 2, die overeenkomt met $c=\sqrt {2}$, is de q -squeezed staat bij het begin, terwijl die in Fig. 3, die overeenkomt met $c=-\sqrt {2}$, de p is -squeezed staat in dezelfde situatie. Door het vergelijken van Fig. 2 en 3 aan elkaar, kunnen we concluderen dat de geometrische fase in de q -squeezed staat is bijna hetzelfde als die in de p -geperste staat.

De effecten van γ over de evolutie van de geometrische fase kan worden bevestigd uit Fig. 2 en 3. De geometrische fase neemt sneller toe wanneer γ is groot. Door het vergelijken van Fig. 2a en 3a met Fig. 2c en 3c, kunnen we bevestigen dat de geometrische fase enigszins snel varieert wanneer ω groter is dan de resonantiehoekfrequentie.

Het tijdsgedrag van de geometrische fase op of nabij de resonantietoestand van het systeem kan van groot belang zijn [22, 23]. Figuren 2b en 3b laten zien dat de geometrische fase zeer snel toeneemt wanneer ω ligt in de buurt van de resonantiehoekfrequentie. Dit betekent dat de golffunctie in deze situatie aanzienlijk varieert in de tijd, omdat de grootte van de geometrische fase gerelateerd is aan de tijdsvariatie van de golffunctie. In feite wordt de amplitude van de draadoscillatie opmerkelijk vergroot in de resonantietoestand. Trouwens, de resonantiehoekfrequenties van zwevende CNT-gebaseerde nanodraadresonatoren zijn niet alleen hoog, maar ook breed afstembaar met factoren van zeer hoge kwaliteit [3]. Om deze reden zullen de vibratiemodi van het systeem lange tijd behouden blijven totdat ze grondig gedempt zijn [11].

Figuur 4 laat zien dat de geometrische fase ook wordt beïnvloed door de amplitude van de drijvende kracht f _d . Als f _d toeneemt, is de toename van de geometrische fase in de tijd snel.

Conclusie

We hebben de geometrische fase in de samengedrukte toestand voor het systeem onderzocht op basis van kwantumdynamica met de Schrödingervergelijking. Met betrekking tot de tijdsafhankelijkheid van de Hamiltoniaan die het systeem beschrijft, is de invariante operatormethode geïntroduceerd, wat een potentieel hulpmiddel is voor het afleiden van kwantumoplossingen in het geval dat de Hamiltoniaan wordt beschreven in termen van tijd. Door middel van deze methode is de analytische formule van de geometrische fase voor de op CNT gebaseerde nanodraadoscillatie verkregen.

Een gedetailleerde analyse van de fase-effecten, die nodig is voor een theoretisch begrip van de mechanische trillingen, is uitgevoerd. Onze ontwikkeling van de geometrische fase is volledig op kwantum gebaseerd met rigoureuze wiskundige evaluaties. De geometrische fase is gevoelig voor de verandering van mechanische parameters en vertoont in een groot aantal gevallen een oscillatie. De invloed van de knijpparameters op de evolutie van de geometrische fase is ook geanalyseerd. We hebben een sterke toename van de accumulatie van geometrische fasen in de tijd bevestigd in de buurt van de resonante hoekfrequentie.

Onze resultaten illustreren het tijdsgedrag van de geometrische fase die verschijnt in de vibratie van een op CNT gebaseerde nanodraad. De analyse van de geometrische fase die in dit werk wordt gegeven, is belangrijk om niet alleen de topologische kenmerken van het systeem te begrijpen, maar ook om de dynamische trillingen van andere op nanodraad gebaseerde mechanische oscillatoren te begrijpen. In het bijzonder hebben we fase-eigenschappen van de resonantietoestand ontwikkeld, waarvan verduidelijking nodig is bij de toepassing van het systeem in kwantuminformatietechnologieën en andere op kwantum gebaseerde industrieën [40]. De vergelijkbare methode en het vergelijkbare raamwerk dat in dit onderzoek wordt gebruikt, kan ook worden uitgebreid naar andere nanosystemen, zoals supergeleidende Fabry-Perot-resonatoren [41], nano-cantilevers [42] en qubit-resonator-atom hybride systemen [43].

Afkortingen

CNT:: Koolstof nanobuisje
EM-golven:: Elektromagnetische golven
TDHS:: Tijdsafhankelijk Hamiltoniaans systeem

Directe groei van enkelkristallijne GaN-nanodraden op met indiumtinoxide gecoat siliciumdioxide Een hoogwaardige rechthoekige Gate U-kanaal-FET's met slechts 2 nm afstand tussen bron- en afvoercontacten

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal