Invloed van het substraat op de LSP-koppelingsgolflengte en sterkte

Resultaat en discussie

Figuur 1a–c toont de schematische illustraties van de structuren voor FDTD-simulaties. De structuur getoond in Fig. 1a vertegenwoordigt de halfbolvormige Au NP's op een diëlektrisch substraat, dat wordt genoemd als structuur A. De structuren getoond in Fig. 1b vertegenwoordigen de sferische Au NP's op een diëlektrisch substraat dat wordt genoemd als structuur B. Ter vergelijking, de structuur C getoond in Fig. 1c, die een hogere symmetrie heeft, wordt ook gebruikt voor simulaties. Voor simulatie zijn de diameters van de Au NP's voor alle structuren ingesteld op 60 nm. De brekingsindices van de media boven de substraten zijn ingesteld als n ₁ = 1 in de meeste gevallen. De brekingsindices van de substraten variëren van n ₂ = 1 tot n ₂ = 2.5. Figuur 1d-f toont de genormaliseerde verstrooiingsspectra van respectievelijk structuren A tot C. Het is duidelijk te zien dat voor structuur A en C de verstrooiingspieken rood verschuiven met de dramatische toename van de brekingsindices van de substraten. Voor structuur B heeft de toename van de brekingsindices van de substraten echter een verwaarloosbaar effect op de verstrooiingspieken.

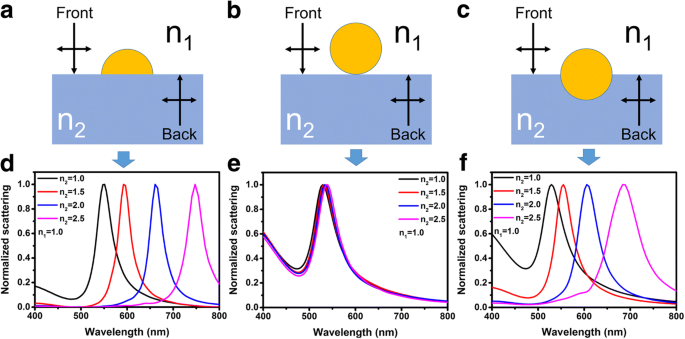
een –c Schematische diagrammen van structuur A tot C gebruikt voor respectievelijk FDTD-simulaties. d –f Genormaliseerde verstrooiingsspectra van structuur A tot C met respectievelijk variërende brekingsindices van het substraat

Figuur 2a toont de golflengte van de LSP-verstrooiingsmaxima versus de brekingsindices van de substraten geëxtraheerd uit Fig. 1. Uit Fig. 2a is de eerste informatie die we kunnen verkrijgen dat wanneer de brekingsindices van substraten toenemen, de verstrooiingspiekgolflengten toenemen sneller dan de lineaire aanname. Dit kan bij benadering worden verklaard door de Mie-theorie. Van Mie-theorie, onder de quasi-statische benadering, de verstrooiende doorsnede van een metalen NP omgeven door een isotroop en niet-absorberend medium met diëlektrische constante ε _m kan worden uitgedrukt als:

waar k is de golfvector van de zich voortplantende golf, a is de straal van een bolvormige metalen NP, en ε vertegenwoordigt de diëlektrische constante van het metaal. Insert in Fig. 2a toont de relatie tussen de verstrooiingspiekgolflengten en de brekingsindices van het medium dat de metalen NP omringt, berekend met behulp van Vgl. (1). Men kan duidelijk de superlineaire relatie zien tussen de verstrooiingspiekgolflengten en de brekingsindices, die vrij gelijkaardig is aan de gesimuleerde resultaten. We kunnen dus de effectieve brekingsindextheorie gebruiken voor verdere discussies. Uit de effectieve brekingsindextheorie, als de verstrooiingspiekgolflengten van Au NP worden omgeven door een oneindig diëlektrisch medium met brekingsindex n _eff gelijk aan die van de Au NP voor verschillende structuren, n _eff kan worden beschouwd als de effectieve brekingsindices van de overeenkomstige structuren. Tabel 1 toont de n _eff verkregen met deze methode.

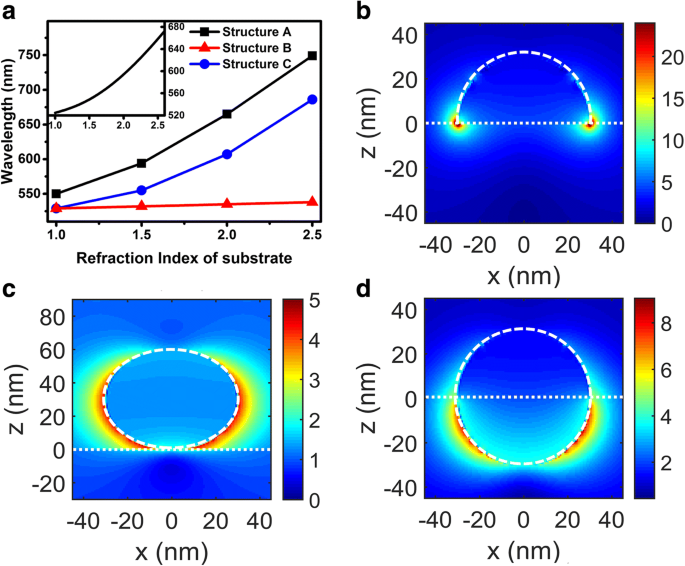
een Verstrooiing van piekgolflengten van verschillende structuren met variërende brekingsindices van het substraat. Het inzetstuk toont de relatie tussen de LSP-koppelingsgolflengte en de brekingsindex van het omringende medium op basis van de Mie-theorie. b –d Polarisatie elektrische veldverdelingen van structuur A tot C met n ₂ = 1,5 bij respectievelijk de corresponderende LSP-koppelingsgolflengte

Met behulp van een lineaire passende vergelijking [36]:

waar μ kan worden beschouwd als de wegingscoëfficiënt om de invloed van de substraatbrekingsindex op de LSP-koppelingsgolflengte te schatten. De invloed van de media boven en onder de interface kan worden ingeschat. Met behulp van de parameters in tabel 1 worden de wegingscoëfficiënten μ van structuur A tot C zijn respectievelijk 0,38 ± 0,02, 0,93 ± 0,01 en 0,25 ± 0,05. Deze resultaten geven aan dat voor structuur B de verstrooiingspiekgolflengte bijna alleen afhankelijk is van de brekingsindex van het medium boven het grensvlak. Voor structuur C speelt de brekingsindex van het substraat een belangrijke rol bij de golflengte van de verstrooiingspiek. Voor structuur A wordt de verstrooiingspiekgolflengte echter beïnvloed door de brekingsindex van de media boven en onder het grensvlak beide.

Deze verschijnselen kunnen worden verklaard door de analyse van elektrische veldverdelingen. Figuur 2b–d toont de elektrische veldamplitudeverdelingen van structuur A tot C met n ₂ = 1,5 bij respectievelijk de overeenkomstige verstrooiingspiekgolflengten. Elektrisch veld dat zich voornamelijk in de buurt van het grensvlak concentreert, zowel het medium boven het grensvlak als het medium onder het grensvlak beïnvloeden de resonantiegolflengten van de LSP's voor respectievelijk structuur A tot C. Deze resultaten bevestigen dat de verdeling van het elektrisch veld goed overeenkomt met de berekende wegingscoëfficiënten omdat de invloed van het omringende medium op de verstrooiingspiekgolflengte kan worden toegeschreven aan de polarisatie van het diëlektrische medium veroorzaakt door het gelokaliseerde elektrische veld.

Van verg. (2), verkrijgen we wanneer n ₂ is vast en n ₁ is afstembaar, de veranderingssnelheid, d.w.z. de helling van de n _eff , is de wegingscoëfficiënt μ . Zo kunnen we de bovenstaande resultaten gebruiken om de LSP-gebaseerde chemische sensor te optimaliseren als het substraat onvermijdelijk is. Op LSP gebaseerde chemische sensor moet de verandering van de brekingsindex van de omgeving detecteren via de LSP-resonantiepiekgolflengteverschuiving Δλ [37]. De gevoeligheid van de sensoren is sterk gerelateerd aan twee parameters, waaronder de shift parameter S = d (Δλ )/d (Δn ) en het cijfer van verdienste FOM = S /FWHM , waar Δn vertegenwoordigt de verandering van de brekingsindex en FWHM is de volledige golf op het halve maximum van de begintoestand [37, 38]. De meeste eerdere onderzoeken naar op LSP gebaseerde sensoren richten zich op het materiaal, de grootte en de vorm van de NP's [39,40,41]. Er zijn echter maar heel weinig rapporten die de invloed van substraat en hun interacties met de metalen NP's bespraken. Afbeelding 3 toont de verstrooiingsspectra van structuur A tot C wanneer n ₁ wordt lineair verhoogd van 1,0 naar 1,5 en n ₂ is vastgesteld op 1.5 of 2.5. Invoegingen weergegeven in alle figuren vertegenwoordigen de verstrooiing piekgolflengten vs. n ₁ . Afbeelding 3a–f laat zien dat de S parameter voor structuur A en B is hoger dan die van structuur C. Tabel 2 geeft een overzicht van de berekende parameters van S , FWHM , en FOM uit Afb. 3. Voor n ₂ = 1.5, de S en FOM parameters voor structuren A en B is veel beter dan die van structuur C. Voor n ₂ = 2.5, hoewel de S parameters voor structuren A en B hoger is dan die wanneer n ₂ = 1.5, de FOM verslechtert vanwege de toename van FWHM .

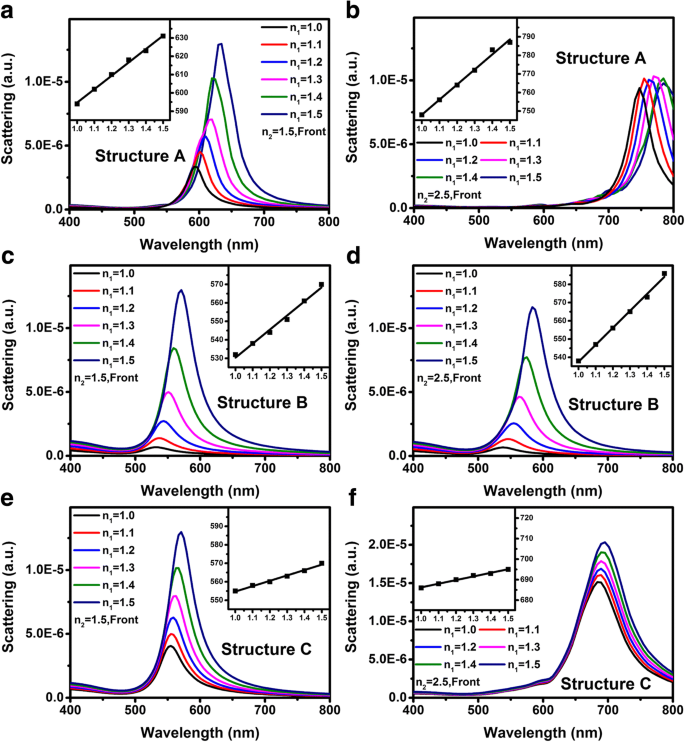
een , c , e Verstrooiingsspectra van structuur A tot C wanneer n ₁ wordt lineair verhoogd van 1,0 naar 1,5. met vaste n ₂ =1,5, respectievelijk. b , d , v Verstrooiingsspectra van structuur A tot C wanneer n ₁ wordt lineair verhoogd van 1,0 naar 1,5, met vaste n ₂ =2,5, respectievelijk. De inzetstukken tonen de relatie tussen verstrooiingspiekgolflengten en n ₁ voor verschillende structuren of substraatbrekingsindices

De bovenstaande discussie gaat helemaal over de LSP-koppelingsgolflengte. Terwijl de LSP-koppelingssterkte een andere waardevolle parameter is voor veel op LSP gebaseerde apparaten zoals LED's, fotodetectoren, zonnecellen en opkomende technieken zoals SERS, TERS en chemische sensoren. Ons eerdere onderzoek gaf aan dat voor structuur A de koppelingssterkte tussen licht en LSP's wordt beïnvloed door de invallende richting van het licht. Dit kan worden toegeschreven aan de verschillende lokale elektrische veldintensiteiten wanneer licht normaal gesproken vanuit de lucht en het substraat invalt [26]. De verhouding van de extinctiepiekintensiteiten wanneer licht van het substraat invalt (aangeduid als achterinval) en de lucht (aangeduid als voorinval) C _B /C _F is gelijk aan n ₂ /n ₁ . Figuur 4 toont de FDTD-gesimuleerde verstrooiingsspectra wanneer licht vanuit verschillende richtingen invalt, geassocieerd met de verstrooiingsspectra van Au NP's omringd door de overeenkomstige effectieve brekingsindices. Figuur 4a-c, d-f vertegenwoordigt de verstrooiingsspectra van respectievelijk structuren A en C. De brekingsindices van het substraat n ₂ zijn respectievelijk 1,5, 2,0 en 2,5 voor Fig. 4a, d, b, e, c, f. n ₁ is vastgesteld op 1.0 voor alle spectra. Net als bij de extinctiespectra, zijn de piekintensiteiten van de verstrooiing wanneer licht van achteren en van voren invalt C _SB /C _SF is gelijk aan n ₂ /n ₁ voor structuur A en C beide.

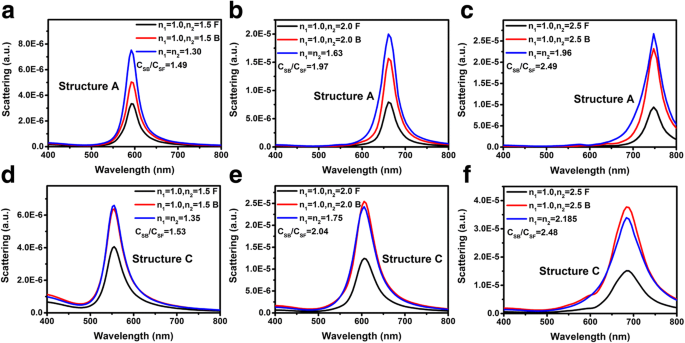
Verstrooiingsspectra voor het variëren van n ₂ = 1,5, 2,0 en 2,5 van structuur A (a –c ) en structuur C (d –f ) respectievelijk. Licht valt normaal uit lucht (aangeduid als zwarte lijnen) en substraten (aangeduid als rode lijnen). De blauwe lijnen tonen de verstrooiingsspectra waarvan de Au NP's omgeven zijn door oneindige diëlektrische media met effectieve brekingsindices

Wanneer we rekening houden met de verstrooiingsspectra van Au NP's omringd door de overeenkomstige effectieve brekingsindices, zijn er verschillen tussen de verstrooiingspiekintensiteiten van structuur A en C. Figuur 5a, b toont de verhoudingen van C _SF /C _Seff en C _SB /C _Seff vs. de brekingsindices van substraten met respectievelijk structuur A en C, waarbij C _Seff is de verstrooiingspiekintensiteit waarvan de Au NP's worden omgeven door oneindige diëlektrische media met effectieve brekingsindices (figuur 4). Voor alle substraten zijn de verhoudingen C _SF /C _Seff en C _SB /C _Seff van structuur A kleiner zijn dan die van structuur C. Dit kan ook worden verklaard door het verschil tussen het lokale elektrische aandrijfveld van structuur A en C.

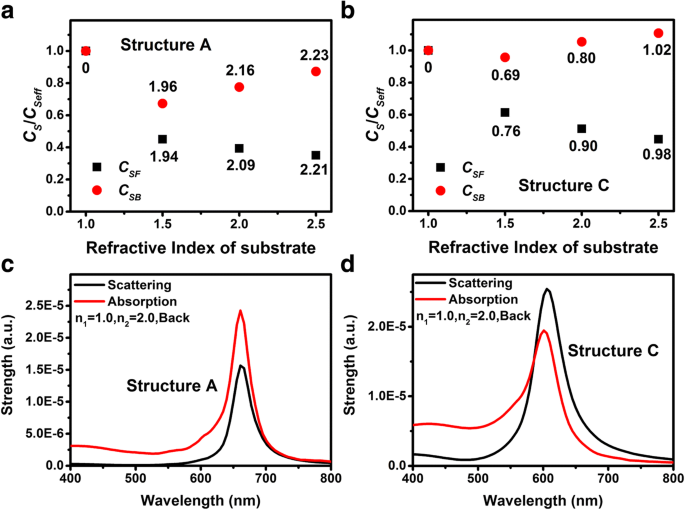
een , b De verhoudingen van koppelingssterkten C _S /C _Seff met verschillende n ₂ van respectievelijk structuur A en structuur C. Zwarte rechthoekige en rode ronde stippen vertegenwoordigen respectievelijk de voor- en achterkant van incidenten. c , d Verstrooiings- en absorptiespectra van structuren A en C met vaste n ₂ = 2.0 wanneer licht van het substraat valt

Op basis van de gewijzigde Fresnel-vergelijkingen [26, 42] kan de intensiteit van het lokale elektrische veld dat wordt aangedreven wanneer licht van de voor- en achterkant invalt, worden geschreven als 2n ₁ E _ik /(n ₁ + n ₂ + A ) en 2n ₂ E _ik /(n ₁ + n ₂ + A ), waarbij E _ik is de elektrische veldintensiteit van de invallende golf, en A =  − ik (ω /c )ρα kan worden beschouwd als een extra parameter die voortkomt uit de LSP's, die evenredig is met de polariseerbaarheid α van de Au NP's en is een positief reëel getal bij de LSP-resonantiefrequentie. Dus de C _SB /C _SF is gelijk aan n ₂ /n ₁ die ook in Fig. 4 wordt getoond. Aan de andere kant is de lokale elektrische veldintensiteit wanneer de Au NP's omgeven door de overeenkomstige effectieve brekingsindex gelijk aan E _ik . Dus de waarde van A parameter kan worden verkregen met behulp van de vergelijking:

De berekende A parameters worden vermeld in de buurt van het corresponderende punt in Fig. 5a, b. Men kan zien dat de waarde van A is heel dichtbij, maar niet precies hetzelfde voor verschillende richtingen van lichtinval. Dit wordt toegeschreven aan het kleine verschil tussen C _SB /C _SF en n ₂ /n ₁ evenals de nauwkeurigheid van de simulatiesoftware. Voor dezelfde structuur met verschillende brekingsindices van het substraat, de A waarde neemt toe met de toename van de brekingsindices van het substraat, wat kan worden toegeschreven aan de verhoogde polariseerbaarheid van de Au NP's met de toename van de LSP-resonantiegolflengte [43,44,45]. Aan de andere kant moet men zich ervan bewust zijn dat de A waarde van structuur A is veel groter dan die van structuur C voor verschillende structuren met dezelfde brekingsindices van het substraat. Het betekent dat de polariseerbaarheid van de Au NP's voor structuur A veel groter is dan die van structuur C, wat kan worden bewezen door Fig. 2b, d. Het is interessant dat hoewel de polariseerbaarheid van de Au NP's van structuur A groter is dan die van structuur C, de verstrooiingspiekintensiteiten van structuur A kleiner zijn dan die van structuur C (figuur 4). Dit kan worden toegeschreven aan de hogere absorptie van structuur A. Figuur 5c, d toont de verstrooiings- en absorptiespectra van respectievelijk structuur A en C, de brekingsindex van het substraat is 2,0 voor beide structuren en licht valt in vanaf de achterkant. Men kan zien dat de absorptie van structuur A veel hoger is dan die van structuur C. Dus voor structuur A wordt de meeste energie die de LSP's exciteert verbruikt via absorptie en niet verstrooid.

Voor structuur B is de verhouding C _SB /C _SF is niet gelijk aan n ₂ /n ₁ . Figuur 6a-c toont de verstrooiingsspectra van structuur B met verschillende substraatbrekingsindices van respectievelijk 1,5, 2,0 en 2,5. C _SB /C _SF van structuur B is kleiner dan n ₂ /n ₁ voor alle substraatbrekingsindices. Zoals schematisch geïllustreerd in Fig. 6d, wanneer licht vanaf de voorkant invalt, kan het lokale elektrische veld worden geschreven als de superpositie van E _ik en E _rF , waar E _rF is de elektrische veldintensiteit van de gereflecteerde golf. De lokale intensiteit van het elektrische veld bij invallend licht kan worden geschreven als \( {E}_{dF}={E}_i+{E}_{rF}=\left[1+\frac{n_1- {n}_2}{n{}_1+{n}_2}\cos \left(\frac{4\pi Pa}{\lambda_{LSP}}\right)\right]{E}_i \), waarbij P is een coëfficiënt die betrekking heeft op de gemiddelde afstand van de oscillerende elektronen en een extra lichtpad wanneer licht zich door de Au NP's voortplant, en de λ _LSP is de resonantiegolflengte van de LSP's. Gezien het feit dat de lokale intensiteit van het elektrische veld van de aandrijving wanneer licht vanaf de achterkant invalt, kan worden geschreven als E _dB = E _tB = 2n ₂ E _ik /(n ₁ + n ₂ ), kan de verhouding van de lokale elektrische veldintensiteiten wanneer licht van de voor- en achterkant invalt worden geschreven als:

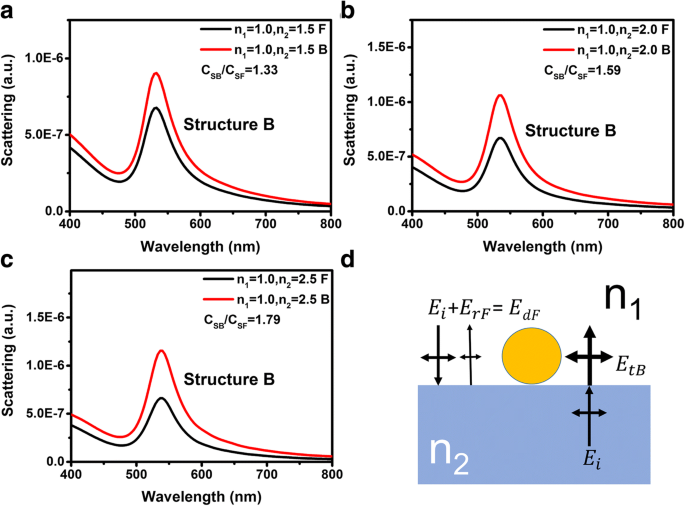
een –c Verstrooiingsspectra voor het variëren van n ₂ =1,5, 2,0 en 2,5 van respectievelijk structuur B. Zwarte en rode lijnen vertegenwoordigen respectievelijk de voor- en achterincidenten. d Schematisch diagram van lokaal elektrisch aandrijfveld van structuur B voor verschillende invalrichtingen

Tabel 3 vermeldde de C _SB /C _SF van structuur B verkregen door de verstrooiingsspectra en de E _dB /E _dF berekend met behulp van vgl. (4) met verschillende P coëfficiënten. Je kunt zien dat wanneer de P coëfficiënt is gelijk aan 1,5, E _dB /E _dF komt goed overeen met de verhoudingen van C _SB /C _SF voor alle ondergronden. De reden waarom P gelijk is aan 1,5 is nog onduidelijk.

Tabel 4 en 5 vermeldden de C _SB /C _SF verkregen door de verstrooiingsspectra en de E _dB /E _dF berekend met behulp van vgl. (4) voor NP's met verschillende geometrische structuren en materialen om de universaliteit van de P . te onderzoeken coëfficiënt. Men kan zien dat voor Au NP's met verschillende groottes, wanneer de P coëfficiënt is gelijk aan 1,5, de verhoudingen van C _SB /C _SF en E _dB /E _dF zijn het vrij goed met elkaar eens wanneer de NP's afgeplat elliptisch of prolaat elliptisch zijn. Tabel 5 laat zien dat de P coëfficiënt van de Ag NP's met verschillende groottes is ook gelijk aan 1,5. Dus de P coëfficiënt is relatief universeel, wat aangeeft dat er een intern mechanisme zou moeten zijn voor de P coëfficiënt en nader diepgaand onderzoek waard.

De bovenstaande discussies zijn gebaseerd op enkele NP. In de praktijk worden echter meestal matrixstructuren van nanodeeltjes bereikt voor onderzoek. Daarom moeten NP-dimeren ter discussie worden gebruikt, omdat de eigenschappen van het nabije veld van de periodieke NP-structuren zullen worden beïnvloed door randvoorwaarde-problemen in FDTD-simulaties. De geometrische structuurparameters van de NP's die worden gebruikt voor de dimeersimulatie zijn vergelijkbaar met die voor de enkele NP die hierboven is besproken, en er wordt een opening van 2 nm ingesteld tussen deze twee NP's. De gesimuleerde resultaten (hier niet getoond) toonden aan dat wanneer de polarisatierichting van normaal invallend licht loodrecht staat op het NP-dimeer, alle eigenschappen hetzelfde zijn als die voor enkel NP. Alle hieronder besproken eigenschappen van het nabije veld zijn dus gebaseerd op een invallend licht waarvan de polarisatierichting evenwijdig is aan het NP-dimeer.

Figuur 7a, b toont de schematische illustraties van respectievelijk halfbolvormige Au-dimeren op een diëlektrisch substraat (structuur A′) en bolvormige Au-dimeren die half in het substraat zijn begraven (structuur C′). Figuur 7c, d toont de verstrooiingsspectra van de dimeren met verschillende substraatbrekingsindices en lichtinvalrichtingen. Men kan zien dat voor structuur A′ en C′ zowel de eerste-orde als de tweede-orde verstrooiingspieken in alle spectra worden waargenomen. In het bijzonder kunnen voor structuur C′ de pieken van de derde orde worden waargenomen wanneer de brekingsindices van het substraat gelijk zijn aan 2 en 2,5. Men kan ook zien dat alle verstrooiingspieken sterk rood verschuiven met de toename van de brekingsindices van het substraat. Dit kan worden verklaard door de amplitudeverdelingen van het elektrische veld bij de overeenkomstige golflengten van de eerste-orde piek voor structuur A′ en C′ zoals weergegeven in respectievelijk Fig. 8a, b, de brekingsindices van het substraat zijn 1,5. Vergelijkbaar met dat zoals getoond in Fig. 2, concentreerde het elektrische veld zich voornamelijk in de buurt van het grensvlak. Dus wanneer licht vanuit verschillende richtingen invalt, is een gelijk aan C _SB /C _SF naar n ₂ /n ₁ kan worden verwacht en zoals aangetoond in Fig. 7c, d. Aan de andere kant, vergeleken met de verstrooiingsspectra zoals getoond in Fig. 4, zijn de verstrooiingspiekintensiteiten van het dimeer veel hoger dan die van de enkele NP. Dit wordt toegeschreven aan de geweldige verbetering van het elektrische veld door de hotspots bij de nanogaten [33].

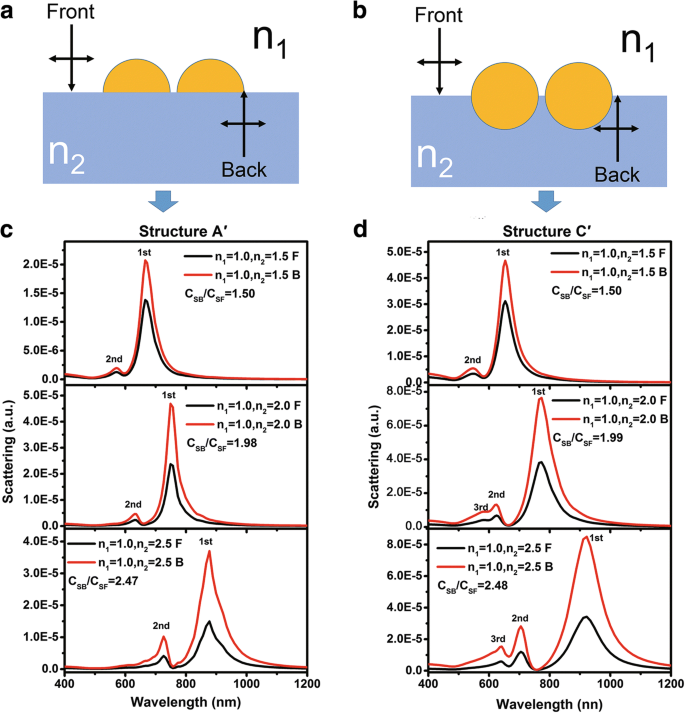
een , b Schematische diagrammen van structuur A′ en C′ respectievelijk gebruikt voor FDTD-simulaties. c , d Verstrooiingsspectra voor het variëren van n ₂ = 1,5, 2,0 en 2,5 van respectievelijk structuur A′ en structuur C′. Licht valt normaal gesproken in de lucht (aangeduid als zwarte lijnen) en substraten (aangegeven als rode lijnen)

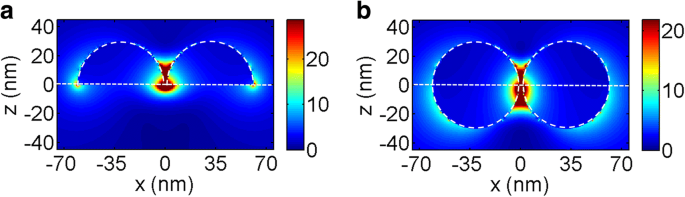
een , b Polarisatie elektrische veldverdelingen van structuur A′ en C′ met n ₂ = 1,5 bij respectievelijk de corresponderende golflengten van de eerste orde piek

Zoals getoond in Fig. 9 is de invloed van de brekingsindex van het substraat echter voor sferische Au dimeren die zich op een diëlektrisch substraat (structuur B′) bevinden iets sterker dan die voor structuur B. De eerste-orde piek roodverschuivingen van 580 tot 614 nm wanneer de brekingsindex van het substraat wordt verhoogd van 1,5 naar 2,5, waarvan groter is dan die voor enkele NP (van 532 tot 538 nm). Dit kan worden toegeschreven aan de amplitudeverdelingen van het elektrische veld bij de overeenkomstige piekgolflengte van de eerste-orde piek voor structuur B′ (Fig. 9d, de brekingsindex van het substraat is 1,5). De elektrische veldintensiteit in het substraat is sterker dan die getoond in figuur 2c. Ook, zoals weergegeven in Fig. 9, is de verhouding van C _SB /C _SF voor NP dimeren van structuur B′ is niet gelijk aan n ₂ /n ₁ , vergelijkbaar met die voor enkele NP. Echter, de P parameter is niet langer een constante als Vgl. (4) wordt nog steeds toegepast. De P parameters kunnen worden berekend tot 1,67, 1,82 en 2,05 wanneer de brekingsindex van het substraat respectievelijk 1,5, 2,0 en 2,5 is. Het verschil tussen de P parameter voor structuur B en B′ behoeft nader onderzoek.

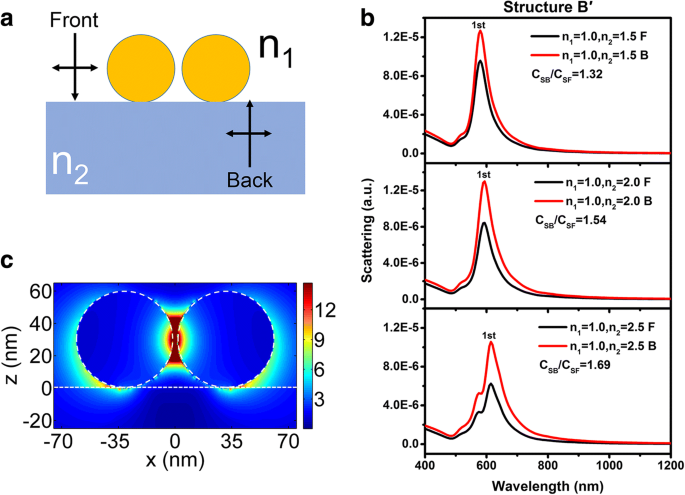
een Schematische diagrammen van structuur B′ gebruikt voor FDTD-simulaties. b Verstrooiingsspectra voor het variëren van n ₂ = 1,5, 2,0 en 2,5 van structuur B′. Licht valt normaal uit lucht (aangeduid als zwarte lijnen) en substraten (aangeduid als rode lijnen). c Polarisatie elektrische veldverdelingen van structuur B′ met n ₂ = 1,5 bij 532 nm