Schatting van supercapacitor-energieopslag op basis van fractionele differentiaalvergelijkingen

Methoden

Het gebruik van poreuze materialen in supercondensatoren en de specifieke manier van ladingsaccumulatie zorgen ervoor dat de traditionele benaderingen op basis van afgeleide modellen van gehele orde niet nauwkeurig genoeg zijn. Veel onderzoekers hebben verschillende oplossingen voorgesteld in de vorm van een combinatie van typische RC elementen met constante of variabele waarden [4, 7]. Maar het blijkt dat er absoluut betere precisie kan worden verkregen met behulp van differentiaalrekening zonder gehele getallen voor het definiëren van de relaties tussen de stroom en spanning van de supercondensator [17, 19]. Bovendien kan een dergelijke oplossing resulteren in een zeer eenvoudige modelstructuur, terwijl deze een zeer hoge nauwkeurigheid biedt [18].

Fractionele volgordeverschil-integrale calculus

Fractionele orde differentiaalrekening is al meer dan 300 jaar bekend. Pas de laatste jaren is het echter populair geworden bij het modelleren van fysische verschijnselen en processen. Er wordt aangenomen dat de beschrijving van dynamica met een afgeleide of integraal van niet-gehele volgorde een van de meest effectieve methoden kan zijn voor het modelleren van reële eigenschappen van veel complexe fenomenen en industriële processen, vooral gebaseerd op nieuwe materialen en technologieën [10, 12, 13 , 32–34].

Non-integer-order differentiaal- of integraalrekening is een generalisatie van klassieke calculus om α te bestellen dat hoort bij de verzameling reële getallen \(\mathcal {R}\). De differento–integrale operator van orde \(\alpha \in \mathcal {R}\) van functie f (t ) op het bereik [a ,t ] kan als volgt worden geschreven

ervan uitgaande dat de functie f (t ) is meerdere malen differentieerbaar en integreerbaar. Wat betreft de operator (1), er zijn veel definities van de realisatie ervan. Dergelijke definities verschillen in eigenschappen en toepassingsgebieden. De meest populaire zijn de Riemann-Liouville, Caputo en Grünwald-Letnikov (GL) definities [34]. De laatste zal in dit artikel worden gebruikt in de vorm

waarbij de binominale \(\alpha \choose j\) als volgt wordt gedefinieerd

Om op discrete momenten een fractioneel model te verkrijgen, wordt de GL-definitie in discrete vorm vereenvoudigd als

Er zijn verschillende discretisatieschema's voor de GL Eq. (4). De meest populaire zijn achterwaartse verschillen (Euler), trapeziumvormige (Tustin) en Al Alaoui-operators. Met behulp van de methode van Euler, de fractionele afgeleide op discrete tijdstippen k kan worden gepresenteerd als

De oneindige som van eerdere monsters moet in echte systemen beperkt zijn tot een eindige waarde vanwege het beperkte geheugen en de beperkte rekentijd. Nu, de afgeknotte of eindige lengte discrete tijd benadering van GL is

waar f (l )=0 voor l <0 en L is de lengte van het model (6) [23]. Het verminderen van het aantal monsters resulteert in een verminderde rekennauwkeurigheid. Dit is belangrijk voor systemen die in een continue tijd werken. Enkele andere soorten oplossingen zijn algoritmen die fractionele differento-integralen benaderen met modellen van gehele orde. Een voorbeeld hiervan zijn Oustaloup recursieve filters [35]. Een ander effectief eindige-lengtemodel is de FFLD, die een combinatie is van het afgeknotte model (6) en een op Laguarre gebaseerd verschil [24, 36, 37].

Alle resultaten van identificatie en energiemetingen worden verkregen op basis van alle monsters in het (lange) observatievenster L , d.w.z. met maximale nauwkeurigheid. Figuur 1 toont de stapreacties van integratie en differentiatie verkregen op basis van (6), voor k =0,1,…,L en voor verschillende waarden van integratie/differentiatievolgorde α . Verschillende waarden van orde aannemen α , kan men verschillende fysieke processen nauwkeuriger modelleren, vooral diffusieprocessen.

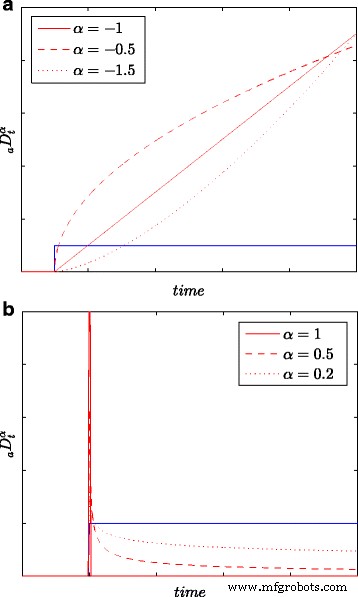
Stapreacties voor integratie (a ) en differentiëren (b ) modellen met verschillende bestellingen α

Parameterschatting voor fractioneel model

De resultaten van alle energiemetingen en identificatieprocedures die in dit document worden gepresenteerd, zijn verkregen voor een supercondensator die is opgeladen vanuit een gecontroleerde spanningsbron. In een dergelijk systeem is de supercondensatorstroom i _C (t ) moet worden begrensd door een weerstand R in serie geschakeld met de supercondensator C (Figuur 2). Schatting van alle supercondensatorparameters wordt uitgevoerd op basis van quadripoolrespons u _C (t ) naar spanningsstap u (t ) bij zijn ingang. De juiste waarde van de afgeleide volgorde kiezen α maakt het mogelijk om rekening te houden met een supercondensatormodel van de fysieke verschijnselen die verband houden met diffusieprocessen die verband houden met de herverdeling van de lading tijdens de laad- en ontlaadprocessen. De parallelle weerstand r _P maakt bovendien modellering van de lekstroom mogelijk. Met behulp van de fractionele differentiaalrekening voor het modelleren van supercondensatoren, kan de modelstructuur van lage complexiteit zijn. Voor supercondensatoren opgeladen door de spanningsbron, bestaat een model uit slechts twee elementen, namelijk een eenvoudige RC quadripool (Fig. 2a). Voor lage capaciteiten is de serieweerstand r _S is van belang (Fig. 2b), terwijl de lekstroom I _L kan bovendien worden weergegeven door de parallelle weerstand r _P (Fig. 2c). Met behulp van de fractionele-ordeberekening om de supercondensator te modelleren, kan de relatie tussen de spanning op de condensatorterminals en de stroom ervan als volgt worden uitgedrukt

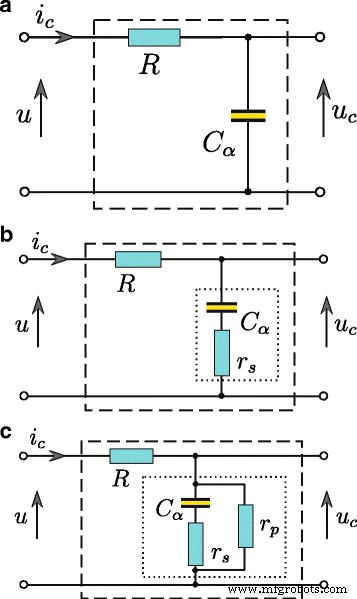
Supercondensator RC modellen, basismodel (a ), uitgebreid met een serieweerstand (b ), en met extra parallelle weerstand (c )

waarbij de operator d ^α /dt ^α betekent een differentiatie-operator van de orde α en de SI-eenheid van C _α is [F/sec ^1−α ]. De basisconfiguratie van supercondensatoren gepresenteerd in figuur 2a kan worden behandeld als een traagheidssysteem van de eerste orde en kan worden weergegeven door de fractionele overdrachtsfunctie

$$ G(s^{\alpha})=\frac{U_{C}(s)}{U(s)}=\frac{1}{Ts^{\alpha} +1}, $$ (8 )

waar T =R C _α . Rekening houdend met de serieweerstand r _S (Fig. 2b), het circuit wordt behandeld als een fasevertragingscorrectiesysteem met de overdrachtsfunctie (vergelijk [24])

$$ G(s^{\alpha})=\frac{1}{T_{1}s^{\alpha}+1}+\frac{T_{2}s^{\alpha}}{T_{1 }s^{\alpha}+1}, $$ (9)

waar T ₁ =C _α (R +r _S ) en T ₂ =r _S C _α . Bovendien, rekening houdend met de parallelle weerstand r _P vertegenwoordigt de lekstroom I _L (Fig. 2c), kan de systeemoverdrachtsfunctie worden uitgedrukt als

$$ G(s^{\alpha})=\frac{T_{2}s^{\alpha} +1}{T_{1}s^{\alpha} +K}, $$ (10)

waar K =R /r _P +1, T ₁ =C (R r _s /r _P +R +r _S ) en T ₂ =r _S C . In het tijdsdomein, Vgl. (10) kan worden weergegeven als

$$ \frac{\mathrm{d}^{\alpha} u_{C}(t)}{\mathrm{d}t^{\alpha}}=\frac{1}{T_{1}}(u (t)-Ku_{C}(t))+\frac{T_{2}}{T_{1}}\frac{\mathrm{d}^{\alpha} u(t)}{\mathrm{d }t^{\alpha}}. $$ (11)

De tijdrespons van het model gedefinieerd door (11) werd verkregen door het om te zetten in de vorm die grafisch wordt weergegeven in Fig. 3, waar integratie- en differentiatiebewerkingen van fractionele orde zijn α . Dit model werd gebruikt tijdens het schattingsproces van supercondensatorparameters. De geteste supercondensator werd geïdentificeerd met behulp van het systeem gepresenteerd in figuur 4a. De controleprocedure van het gehele systeem is ontwikkeld met behulp van de Matlab/Simulink-software met xPC Toolbox. Het systeem bestond uit een desktop-pc (xPC Target) met de geïnstalleerde meetkaart NI-DAQ en mastercomputer (xPC Host). De computers waren met elkaar verbonden via het Ethernet-netwerk. De supercondensator werd geladen en ontladen door een (spanningsgestuurde) spanningsbron (Fig. 4b) met een stroomrendement tot ± -3 A. Het meetsysteem werd bediend met de bemonsteringsfrequentie van 100 Hz, terwijl alle metingen en analoge stuursignalen werden verwerkt met een resolutie van 16 bits [25].

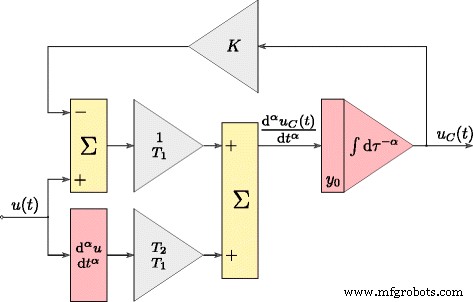
Matlab-structuur van supercondensatormodel in tijddomein

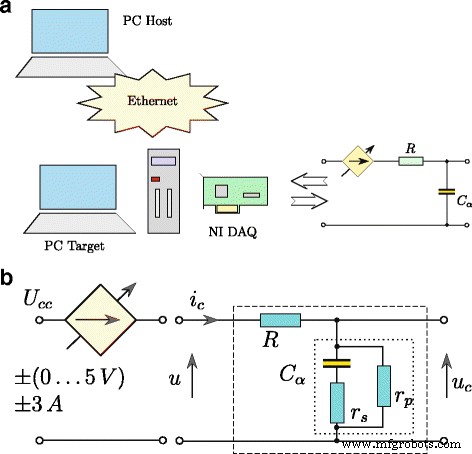
Opbouw meetsysteem (a ) en supercondensator laad-/ontlaadschema (b )

De belangrijkste methode voor het bepalen van de dynamische eigenschappen van een systeem is gebaseerd op de analyse van de staprespons [38]. Met betrekking tot het systeemmodel maakt deze methode het mogelijk om de parameters ervan te schatten. Voor deze studie is het stapsignaal met verschillende spanningen (0,5/1,0/1,5/2,0/2,7 V) en constante duur (500 s) gebruikt (zie Fig. 5 en Tabel 2). Aan de andere kant is een van de typische toepassingen van supercondensatoren de accumulatie of levering van energie aan de voedingssystemen. In dit geval is de spanningsveranderingssnelheid vrij klein. Om het te simuleren, werd het signaal van 400 mVpp en 0,03 rad/s met een offset van 2 V gebruikt (Fig. 6). Om de invloed van de spannings- en frequentieveranderingen op geschatte parameters te onderzoeken, werden bovendien verschillende waarden van deze laatste gebruikt (zie tabel 3).

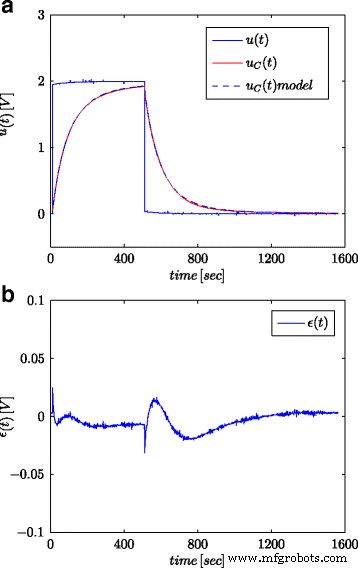
Stapreacties voor geteste supercondensator en zijn fractionele model (a ) en de modelreactiefout (b )

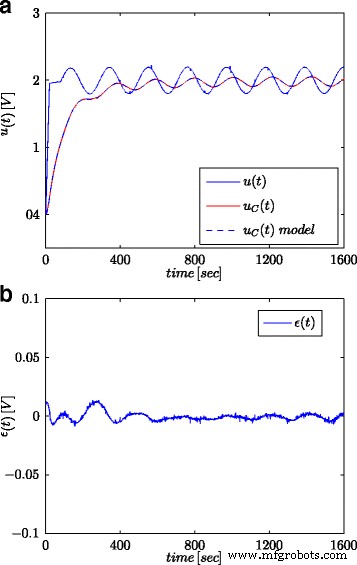
Sinusvormige golfreacties voor geteste supercondensator en zijn fractionele model (a ) en de modelreactiefout (b )

Er zijn verschillende methoden voor het schatten van modelparameters. Het belangrijkste doel van de identificatieprocedure in het tijdsdomein die in dit werk werd toegepast, was het schatten van de vector van onbekende parameters θ =[α ,C _α ,r _S ,r _P ] van fractioneel model gepresenteerd door (11). De kleinste-kwadratenmethode werd gebruikt om de initiële fout te minimaliseren. Een optimalisatiecriterium omvatte het minimaliseren van de standaardfout \(\|\epsilon (k)\|_{2}^{2}\), waarbij

$$ \epsilon(k)=u_{C}(k)-\hat{u}_{C}(k), $$ (12)

waar u _C (k ) is de uitgangsspanning gemeten van het geteste systeem op moment k , terwijl \(\hat {u}_{C}(k)\) de uitgangsspanning is van het beschouwde model voor het ingangssignaal u (k ). Het identificatieprobleem is nu teruggebracht tot het vinden van een parametervector θ ∈Θ _advertentie dat zou het kwadraatcriterium J . minimaliseren zodanig dat

$$ \min_{\theta\in\Theta_{ad}} \left\{ J=\sum_{0}^{N} {\epsilon(k)^{T}\epsilon(k)}\right\} , $$ (13)

waar Θ _advertentie geeft de reeks toegestane parameterwaarden aan en N betekent de simulatietijd. Er zijn veel optimalisatie-algoritmen die kunnen worden gebruikt om het probleem op te lossen (13). De resultaten die in dit artikel worden gepresenteerd, zijn verkregen door het genetische algoritme te implementeren in de Matlab-omgeving.

Energieberekening

Een verandering in de energie opgeslagen in de supercondensator hangt af van het vermogen dat per tijdseenheid aan de condensator wordt geleverd en kan als volgt worden beschreven

$$ \mathrm{d}E(t) =P(t)\mathrm{d}t. $$ (14)

Door het aan de condensator geleverde vermogen uit te drukken als een product van de stroom en spanning op de condensatoraansluitingen, wordt de verandering in energie op een gegeven moment t kan worden uitgedrukt als

$$ \mathrm{d}E(t) =u_{C}(t)i_{C}(t)\mathrm{d}t. $$ (15)

De totale energie gedurende het tijdsinterval [t ₁ ,t ₂ ] kan worden verkregen door de energieveranderingen over die tijd te integreren

$$ E_{tot}=\int_{t_{1}}^{t_{2}}\mathrm{d}E(t)=\int_{t_{1}}^{t_{2}}u_{C }(t)i_{C}(t)\wiskunde{d}t. $$ (16)

Rekening houdend met Eq. (7), de totale energieopslag kan worden bepaald als

$$ E_{tot}=C_{\alpha}\int_{t_{1}}^{t_{2}}u_{C}(t)\frac{\mathrm{d}^{\alpha} u_{C }(t)}{\mathrm{d}t^{\alpha}}\mathrm{d}t. $$ (17)

Ervan uitgaande dat t ₁ =0 en \(E_{t_{1}}=0\), de totale energie opgeslagen in de supercondensator gedurende het tijdsinterval [0,t ] is

$$ E(t)=C_{\alpha}\int_{0}^{t}u_{C}(\tau)\frac{\mathrm{d}^{\alpha} u_{C}(\tau) }{\mathrm{d}\tau^{\alpha}}\mathrm{d}\tau. $$ (18)

Merk op dat voor α =1 Vergelijking (18) kan worden teruggebracht tot de klassieke

$$ E(t)=\frac{1}{2}Cu_{C}(t)^{2}. $$ (19)

Resultaten en discussie

Aanvankelijk werd de procedure voor het schatten van de parametervector van het supercondensatormodel met behulp van de fractionele calculus uitgevoerd. De schatting werd uitgevoerd op basis van het systeem gepresenteerd in figuur 2c, waarbij een spanningsstap of sinusoïdale golf aan de ingang werd gegenereerd. De modelantwoorden werden berekend op basis van (11). De resultaten die door de twee identificatieprocedures worden verkregen, zijn zeer vergelijkbaar, vooral in het geval van fractionele capaciteit C _α en de fractionele volgorde α (zie tabel 1). Enkele verschillen in de schattingen van serieweerstand r _S kan een gevolg zijn van de afhankelijkheid van de frequentie. Het stapsignaal bestaat uit veel hoogfrequente harmonischen, terwijl de sinusvormige golf er slechts één is - de 0,03 rad/s. De gepresenteerde resultaten zijn verkregen voor de commerciële supercondensator Samwha Green–Cap EDLC(DB), beoordeeld als 2,7 V met 100 F nominale capaciteit en 8 mΩ maximale equivalente serieweerstand (r _S ) bij 1 kHz.

Figuren 5a en 6a tonen de gemeten supercondensatorspanning en de berekende modelresponsen, voor respectievelijk stap- en sinusvormige signalen, terwijl Fig. 5b en 6b tonen de modelreactiefout.

Alle verkregen resultaten laten een hoge consistentie zien tussen modelreacties en echte metingen, ondanks het feit dat relatief eenvoudige modellen werden voorgesteld. Sommige discrepanties kunnen het gevolg zijn van het feit dat modelparameters moeten worden geschat in het systeem van supercondensator geladen en ontladen met behulp van de huidige bron [25]. Ook zeer hoge schattingen van r _P kan suggereren dat deze weerstand zou kunnen worden uitgesloten van het supercondensatormodel dat wordt getoond in figuur 2c. Die zeer hoge schattingen en hun grote verschillen voor verschillende ingangen geven aan dat de testsignalen die worden gebruikt om deze parameter te schatten, niet juist zijn. Het model (10) is als meest algemene vorm gebruikt. Om al zijn parameters nauwkeurig te bepalen, was het echter noodzakelijk om andere procedures en testsignalen te gebruiken. De waarde van r _P kenmerkt de lekstroom I _L en moet worden bepaald met behulp van het constante spanningssignaal, maar voor een zeer lange tijd - in de orde van enkele tientallen uren.

Hoewel het belangrijkste doel van het onderzoek het meten van energie was, hadden verschillende excitatiecondities een grote invloed op alle parameterschattingen (zie tabel 2). De toename van de amplitude van de spanningsstap veranderde bijvoorbeeld de fractionele integratievolgorde aanzienlijk, als gevolg van een toenemend effect van de diffusieverschijnselen in de supercondensator. Uit tabel 2 blijkt ook dat de supercondensator vrij niet-lineair is. Als gevolg van de veranderingen in de integratievolgorde wordt ook de variatie van de fractionele capaciteit waargenomen. Dit geldt ook voor sinusoïdale excitatie. De waarden van geschatte parameters—vooral α en C _α —afhankelijk van de amplitude en frequentie (zie tabel 3). Voor lage frequenties is de amplitudewaarde belangrijk, terwijl voor hogere frequenties de supercondensator zich gedraagt ​​alsof hij wordt aangeslagen met een constante spanning.

Energieberekening

Figuren 7a en 8a tonen gemeten waarden van de spanning en stroom van de supercondensator voor de configuratie zoals weergegeven in figuur 4b. Deze waarden werden gebruikt voor de berekening van de totale energie opgeslagen in de condensator (aangeduid als E ₁ in Fig. 7b en 8b) volgens (16). Net als voor parameteridentificatieprocessen, werden de berekeningen uitgevoerd voor zowel de spanningsstap als de sinusoïdale golf aan de systeemingang. De energie berekend op een dergelijke manier voor elke keer dat t werd vergeleken met energie berekend op basis van de spanning en capaciteit in overeenstemming met (19) (gemarkeerd als E ₃ in Fig. 7b en 8b) en energie berekend met fractionele-orde calculus (gemarkeerd als E ₂ in Fig. 7b en 8b) volgens (18). Voor vgl. (19), werd een nominale waarde van supercondensator aangenomen (C _n ), terwijl in (18) de waarde verkregen uit het schattingsproces zoals weergegeven in Tabel 1 werd gebruikt. Figuur 7b toont resultaten van metingen en energieberekeningen voor spanningsstap, terwijl figuur 8b dezelfde hoeveelheden toont voor sinusoïdale golven. Vergelijkbare berekeningen werden gemaakt voor verschillende spanningsstappen en sinusoïdale excitaties. Figuur 9a, b toont een voorbeeld van gemeten en berekende energieën voor twee spanningsstappen van respectievelijk 0,5 V en 2,7 V. Figuur 10 toont de energieveranderingen voor een sinusvormig signaal met de frequentie van 0,03 rad/sec en verschillende amplitudes van 0,1/0,25/0,5 en 0,7 V. Het is te zien dat de verschillen in de bepaalde energiewaarden overeenkomen met verschillen in de geschatte waarden van de fractionele orde α . Hoe groter het verschil met de waarde − 1, hoe groter het verschil in de berekende energieën.

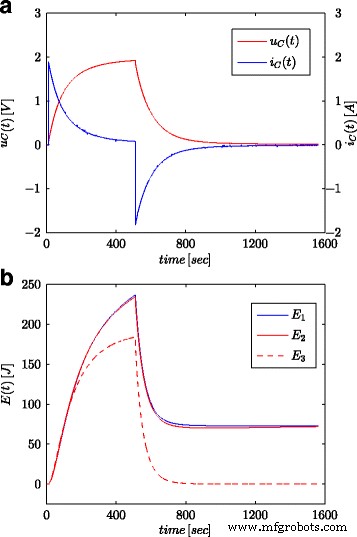
Stapreacties voor supercondensatorspanning en -stroom (a ) en berekende energiewaarden (b )

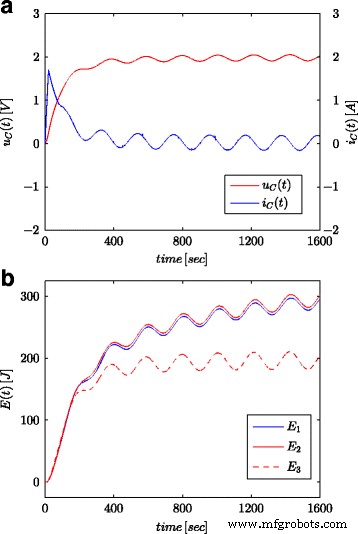
Sinusvormige reacties voor supercondensatorspanning en stroom (a ) en berekende energiewaarden (b )

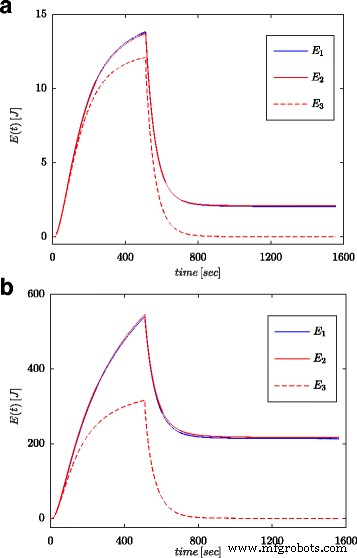
Energiehoeveelheden berekend voor stapexcitaties van 0,5 V (a ) en 2,7 V (b )

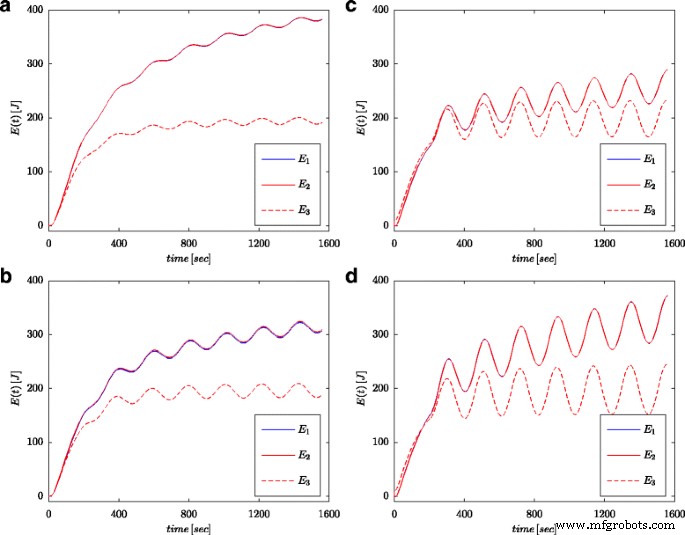
Energiehoeveelheden berekend voor sinusoïdale excitaties met frequentie 0,03 rad/s en amplitudes 0,1 V (a ), 0,25 V (b ), 0,5 V (c ), en 0,7 V (d )

Discussie

Het gebruik van elektroden van poreus materiaal in supercondensatoren in de vorm van actieve koolstof geïsoleerd door een zeer dunne separator en het gebruik van ladingsaccumulatiemechanismen als zogenaamde dubbellaags, geeft een enorme toename van hun capaciteit. De toepassing van nieuwe materialen en nieuwe ontwerpoplossingen leidt er echter toe dat traditionele wiskundige berekeningen in de vorm van afgeleiden van gehele getallen en integralen onnauwkeurig lijken. De uitgevoerde metingen en berekeningen bewijzen de fractionele aard van supercondensatoren. Door correcte schatting van niet-gehele volgorde α van afgeleide/integraal, kan men fenomenen en processen die plaatsvinden in de supercondensator nauwkeurig modelleren met behulp van eenvoudige wiskundige modellen.

Rekening houdend met de werkelijke waarde van de geaccumuleerde energie bepaald door (16), onderschat het integer-orde-model met nominale parameters (19) de hoeveelheid energie, terwijl het fractionele model (18) bijna dezelfde waarde aangeeft.

De uitgevoerde testen en metingen hadden betrekking op het laden en ontladen van de supercondensator door een spanningsbron. Onder industriële omstandigheden worden supercondensatoren meestal geladen en ontladen door stroombronnen. Dit kan de aard van het systeem veranderen, omdat de condensator niet langer een traagheidssysteem is, maar een typisch integrerend systeem wordt. De door auteur uitgevoerde metingen wijzen echter ook op het optreden van diffusieprocessen in dergelijke gevallen. Hoe dan ook, het nut van de Gründwald-Letnikov-derivaat/integraal wordt hier bevestigd. Een ander probleem houdt verband met de implementatie van de operator GL differento-integraal als bijvoorbeeld het eindige of afgeknotte GL-verschil (6), wat rekenkundig belastend kan zijn. In toekomstig onderzoek zullen we de Oustaloup [35] en FFLD [24, 36, 37] benaderingen vergelijken om het implementatieprobleem effectief op te lossen.

De hoeveelheid energieopslag in supercondensator die alleen wordt berekend op basis van de gemeten waarde van de klemspanning van de supercondensator en met behulp van model (19) is niet geschikt. Het model (19) is alleen geldig als de condensatorstroom wordt gekenmerkt door de afgeleide van gehele getallen van de condensatorspanning (i _C (t )=du _C (t )/dt ). Dit geldt niet voor supercondensator als gevolg van de constructie en het gebruik van speciale materialen. Hetzelfde probleem doet zich echter voor bij zeer grote supercondensatoren die worden opgeladen door de stroombron. Er zijn ook vrij nieuwe elementen als super-batterijen. In al deze toepassingen worden de huidige veranderingen niet gekenmerkt door de gehele-orde afgeleide van de klemspanning als gevolg van de specifieke eigenschappen van deze elementen.