Hoe bouw je een variabele auto-encoder met TensorFlow

Leer de belangrijkste onderdelen van een auto-encoder, hoe een variatie-auto-encoder deze verbetert en hoe je een variatie-auto-encoder bouwt en traint met TensorFlow.

In de loop der jaren hebben we gezien dat veel vakgebieden en industrieën de kracht van kunstmatige intelligentie (AI) gebruiken om de grenzen van onderzoek te verleggen. Datacompressie en -reconstructie is geen uitzondering, waarbij de toepassing van kunstmatige intelligentie kan worden gebruikt om robuustere systemen te bouwen.

In dit artikel gaan we kijken naar een zeer populaire use-case van AI om gegevens te comprimeren en de gecomprimeerde gegevens te reconstrueren met een autoencoder.

Autoencoder-applicaties

Autoencoders hebben de aandacht getrokken van veel mensen in machine learning, een feit dat duidelijk werd door de verbetering van autoencoders en de uitvinding van verschillende varianten. Ze hebben een aantal veelbelovende (zo niet state-of-the-art) resultaten opgeleverd op verschillende gebieden, zoals neurale machinevertaling, medicijnontdekking, beeldruisonderdrukking en verschillende andere.

Delen van de Autoencoder

Autoencoders leren, zoals de meeste neurale netwerken, door gradiënten achteruit te verspreiden om een ​​reeks gewichten te optimaliseren, maar het meest opvallende verschil tussen de architectuur van autoencoders en die van de meeste neurale netwerken is een knelpunt. Dit knelpunt is een manier om onze gegevens te comprimeren tot een weergave van lagere dimensies. Twee andere belangrijke onderdelen van een autoencoder zijn de encoder en decoder.

Het samensmelten van deze drie componenten vormt een "vanille" auto-encoder, hoewel meer geavanceerde componenten enkele extra componenten kunnen hebben.

Laten we deze componenten afzonderlijk bekijken.

Encoder

Dit is de eerste fase van datacompressie en -reconstructie en het zorgt in feite voor de datacompressiefase. De encoder is een feed-forward neuraal netwerk dat gegevenskenmerken opneemt (zoals pixels in het geval van beeldcompressie) en een latente vector uitvoert met een grootte die kleiner is dan de grootte van de gegevenskenmerken.

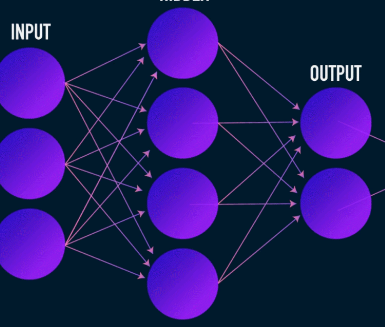
Afbeelding gebruikt met dank aan James Loy

Om de reconstructie van de gegevens robuust te maken, optimaliseert de encoder zijn gewichten tijdens de training om de belangrijkste kenmerken van de invoergegevensrepresentatie in de kleine latente vector te persen. Dit zorgt ervoor dat de decoder voldoende informatie heeft over de invoergegevens om de gegevens met minimaal verlies te reconstrueren.

Latente vector (knelpunt)

Het knelpunt of de latente vectorcomponent van de autoencoder is het meest cruciale onderdeel - en het wordt belangrijker wanneer we de grootte moeten selecteren.

De uitvoer van de encoder geeft ons de latente vector en wordt verondersteld de belangrijkste kenmerkrepresentaties van onze invoergegevens te bevatten. Het dient ook als invoer voor het decodergedeelte en verspreidt de bruikbare representatie naar de decoder voor reconstructie.

Door een kleiner formaat voor de latente vector te kiezen, krijgen we een weergave van de invoergegevensfuncties met minder informatie over de invoergegevens. Door een veel grotere latente vectorgrootte te kiezen, wordt het hele idee van compressie met auto-encoders gebagatelliseerd en worden ook de rekenkosten verhoogd.

Decoder

Deze fase voltooit ons datacompressie- en reconstructieproces. Net als de encoder is dit onderdeel ook een feed-forward neuraal netwerk, maar het ziet er structureel iets anders uit dan de encoder. Dit verschil komt voort uit het feit dat de decoder een latente vector als invoer neemt die kleiner is dan die van de uitvoer van de decoder.

De functie van de decoder is om een ​​uitvoer te genereren van de latente vector die zeer dicht bij de invoer ligt.

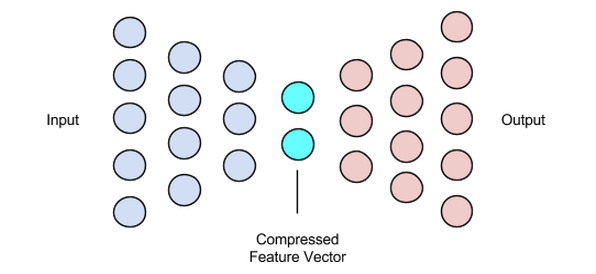
Afbeelding gebruikt met dank aan Chiman Kwan

Auto-encoders trainen

Meestal bouwen we bij het trainen van auto-encoders deze componenten samen in plaats van ze onafhankelijk te bouwen. We trainen ze end-to-end met een optimalisatie-algoritme zoals gradient descent of de ADAM-optimizer.

Verliesfuncties

Een deel van de autoencoder-trainingsprocedure dat het bespreken waard is, is de verliesfunctie. Gegevensreconstructie is een generatietaak en, in tegenstelling tot andere machine learning-taken waarbij het ons doel is om de kans op het voorspellen van de juiste klasse te maximaliseren, sturen we ons netwerk aan om een ​​uitvoer te produceren die dicht bij de invoer ligt.

We kunnen dit doel bereiken met verschillende verliesfuncties zoals l1, l2, mean squared error en een paar andere. Wat deze verliesfuncties gemeen hebben, is dat ze het verschil meten (d.w.z. hoe ver of identiek) tussen invoer en uitvoer, waardoor elk van hen een geschikte keuze is.

Autoencoder-netwerken

Al die tijd hebben we een meerlaags perceptron gebruikt om zowel onze encoder als decoder te ontwerpen, maar het blijkt dat we meer gespecialiseerde frameworks kunnen gebruiken, zoals convolutionele neurale netwerken (CNN's) om meer ruimtelijke informatie over onze invoergegevens in het geval van compressie van beeldgegevens.

Verrassend genoeg heeft onderzoek aangetoond dat terugkerende netwerken die worden gebruikt als auto-encoders voor tekstgegevens heel goed werken, maar daar gaan we in het kader van dit artikel niet op in. Het concept van een encoder-latente vector-decoder die in de meerlaagse perceptron wordt gebruikt, geldt nog steeds voor convolutionele autoencoders. Het enige verschil is dat we de decoder en encoder ontwerpen met convolutionele lagen.

Al deze autoencoder-netwerken zouden redelijk goed werken voor de compressietaak, maar er is één probleem.

De netwerken die we hebben besproken, hebben geen creativiteit. Wat ik bedoel met nul creativiteit is dat ze alleen resultaten kunnen genereren die ze hebben gezien of waarmee ze zijn getraind.

We kunnen een zekere mate van creativiteit opwekken door ons architectuurontwerp een beetje aan te passen. Het resultaat staat bekend als een variatie-autoencoder.

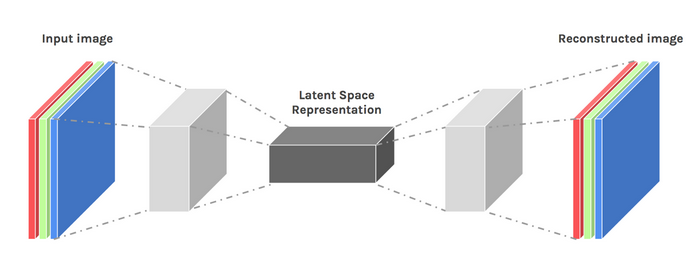
Afbeelding gebruikt met dank aan Dawid Kopczyk

Variationele auto-encoder

De variatie-autoencoder introduceert twee belangrijke ontwerpwijzigingen:

• In plaats van de invoer te vertalen naar een latente codering, voeren we twee parametervectoren uit:gemiddelde en variantie.
• Een extra verliesterm, het KL-divergentieverlies, wordt toegevoegd aan de initiële verliesfunctie.

Het idee achter de variabele autoencoder is dat we willen dat onze decoder onze gegevens reconstrueert met behulp van latente vectoren die zijn gesampled uit distributies die zijn geparametreerd door een gemiddelde vector en variantievector die door de encoder worden gegenereerd.

Sampling-functies van een distributie geven de decoder een gecontroleerde ruimte om van te genereren. Na het trainen van een variabele autoencoder, genereert de encoder telkens wanneer we een voorwaartse doorgang met invoergegevens uitvoeren een gemiddelde en variantievector die verantwoordelijk is voor het bepalen van de distributie waaruit de latente vector moet worden bemonsterd.

De gemiddelde vector bepaalt waar de codering van invoergegevens rond moet worden gecentreerd en de variantie bepaalt de radiale ruimte of cirkel waar we de codering uit willen kiezen om een ​​realistische uitvoer te genereren. Dit betekent dat onze variatie-autoencoder bij elke voorwaartse doorgang met dezelfde invoergegevens verschillende varianten van de uitvoer kan genereren, gecentreerd rond de gemiddelde vector en binnen de variantieruimte.

Ter vergelijking:als we kijken naar een standaard autoencoder, wanneer we proberen een uitvoer te genereren waarop het netwerk niet is getraind, genereert deze onrealistische uitvoer vanwege discontinuïteit in de latente vectorruimte die de encoder produceert.

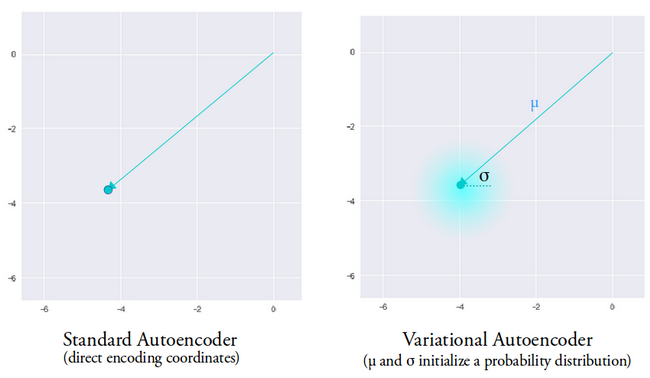
Afbeelding gebruikt met dank aan Irhum Shafkat

Nu we een intuïtief begrip hebben van een variabele autoencoder, laten we eens kijken hoe we er een kunnen bouwen in TensorFlow.

TensorFlow-code voor een variabele auto-encoder

We beginnen ons voorbeeld door onze dataset klaar te maken. Voor de eenvoud gebruiken we de MNIST-dataset.

(train_images, _), (test_images, _) =tf.keras.datasets.mnist.load_data()

train_images =train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')

test_images =test_images.reshape(test_images.shape[0], 28, 28, 1).astype('float32')

# Normaliseren van de afbeeldingen tot het bereik van [0., 1.]

train_images /=255.

test_images /=255.

# Binarisatie

train_images[train_images>=.5] =1.

train_images[train_images <.5] =0.

test_images[test_images>=.5] =1.

test_images[test_images <.5] =0.

TRAIN_BUF =60000

BATCH_SIZE =100

TEST_BUF =10000

train_dataset =tf.data.Dataset.from_tensor_slices(train_images).shuffle(TRAIN_BUF).batch(BATCH_SIZE)

test_dataset =tf.data.Dataset.from_tensor_slices(test_images).shuffle(TEST_BUF).batch(BATCH_SIZE)

Verkrijg dataset en bereid deze voor op de taak.

klasse CVAE(tf.keras.Model):

def __init__(zelf, latent_dim):

super(CVAE, zelf).__init__()

self.latent_dim =latent_dim

self.inference_net =tf.keras.Sequential(

[

tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),

tf.keras.layers.Conv2D(

filters=32, kernel_size=3, strides=(2, 2), activatie='relu'),

tf.keras.layers.Conv2D(

filters=64, kernel_size=3, strides=(2, 2), activatie='relu'),

tf.keras.layers.Flatten(),

# Geen activering

tf.keras.layers.Dense(latent_dim + latent_dim),

]

)

self.generative_net =tf.keras.Sequential(

[

tf.keras.layers.InputLayer(input_shape=(latent_dim,)),

tf.keras.layers.Dense(units=7*7*32, activatie=tf.nn.relu),

tf.keras.layers.Reshape(target_shape=(7, 7, 32)),

tf.keras.layers.Conv2DTranspose(

filters=64,

kernel_size=3,

strides=(2, 2),

padding="SAME",

activatie='relu'),

tf.keras.layers.Conv2DTranspose(

filters=32,

kernel_size=3,

strides=(2, 2),

padding="SAME",

activatie='relu'),

# Geen activering

tf.keras.layers.Conv2DTranspose(

filters=1, kernel_size=3, strides=(1, 1), padding="SAME"),

]

)

@tf.function

def sample(self, eps=None):

als eps Geen is:

eps =tf.random.normal(shape=(100, self.latent_dim))

return self.decode(eps, apply_sigmoid=True)

def encode(self, x):

mean, logvar =tf.split(self.inference_net(x), num_or_size_splits=2, axis=1)

return mean, logvar

def reparameterize(self, mean, logvar):

eps =tf.random.normal(shape=mean.shape)

return eps * tf.exp(logvar * .5) + mean

def decode(self, z, apply_sigmoid=False):

logits =self.generative_net(z)

if apply_sigmoid:

probs =tf.sigmoid(logits)

retourproblemen

logits retourneren

De twee codefragmenten bereiden onze dataset voor en bouwen ons variabele autoencoder-model. In het modelcodefragment zijn er een aantal hulpfuncties om codering, bemonstering en decodering uit te voeren.

Herparameterisatie voor computergradiënten

Er is een herparametreerfunctie die we niet hebben besproken, maar die een zeer cruciaal probleem oplost in ons gevarieerde autoencoder-netwerk. Bedenk dat we tijdens de decoderingsfase monsters nemen van de latente vectorcodering van een distributie die wordt gecontroleerd door de gemiddelde en variantievector die door de encoder wordt gegenereerd. Dit genereert geen probleem bij het voorwaarts verspreiden van gegevens via ons netwerk, maar veroorzaakt een groot probleem bij het terugverspreiden van gradiënten van de decoder naar de encoder, aangezien de bemonsteringsbewerking niet-differentieerbaar is.

In eenvoudige bewoordingen kunnen we geen gradiënten berekenen op basis van een steekproefbewerking.

Een goede oplossing voor dit probleem is het toepassen van de herparameterisatietruc. Dit werkt door eerst een standaard Gauss-verdeling van gemiddelde 0 en variantie 1 te genereren en vervolgens een differentieerbare optel- en vermenigvuldigingsbewerking op deze verdeling uit te voeren met het gemiddelde en de variantie gegenereerd door de encoder.

Merk op dat we de variantie in de code omzetten in logaritmeruimte. Dit om de numerieke stabiliteit te garanderen. De extra verliesterm, het Kullback-Leibler-divergentieverlies, is geïntroduceerd om ervoor te zorgen dat de verdelingen die we genereren zo dicht mogelijk bij een standaard Gauss-verdeling met gemiddelde 0 en variantie 1 liggen.

Door de gemiddelden van de distributies naar nul te brengen, zorgt u ervoor dat de distributies die we genereren zeer dicht bij elkaar liggen om discontinuïteiten tussen distributies te voorkomen. Een variantie in de buurt van 1 betekent dat we een meer gematigde (d.w.z. niet erg grote en niet erg kleine) ruimte hebben om coderingen van te genereren.

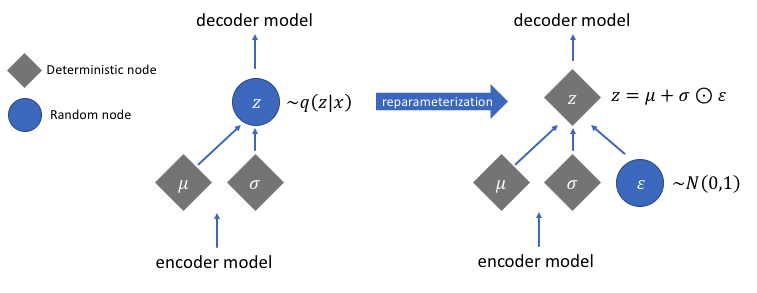
Afbeelding gebruikt met dank aan Jeremy Jordan

Na het uitvoeren van de herparameterisatietruc, lijkt de verdeling die wordt verkregen door de variantievector te vermenigvuldigen met een standaard Gauss-verdeling en het resultaat op te tellen bij de gemiddelde vector, sterk op de verdeling die onmiddellijk wordt gecontroleerd door de gemiddelde en variantievectoren.

Eenvoudige stappen om een ​​variabele auto-encoder te bouwen

Laten we deze tutorial afronden door de stappen samen te vatten voor het bouwen van een variabele autoencoder:

1. Bouw de encoder- en decodernetwerken.
2. Pas een herparametriseringstruc toe tussen encoder en decoder om back-propagatie mogelijk te maken.
3. Train beide netwerken end-to-end.

De volledige code die hierboven is gebruikt, is te vinden op de officiële TensorFlow-website.

Aanbevolen afbeelding gewijzigd van Chiman Kwan