19 Unit 2:Programmeerbare assen en positioneringssystemen voor CNC-bewerkingsmachines
DOELSTELLING
Na het voltooien van deze unit, zou je in staat moeten zijn om:
- Begrijp het cartesiaanse coördinatensysteem.
- Begrijp de cartesiaanse coördinaten van het vliegtuig.
- Begrijp de cartesiaanse coördinaten van de driedimensionale ruimte.
- Begrijp de vier kwadranten.
- Leg het verschil uit tussen polair en rechthoekig gecoördineerd.
- Identificeer de programmeerbare assen op een CNC-bewerking.
HET CARTESIAN CORDINATEN SYSTEEM
Cartesiaanse coördinaten maken het mogelijk om de locatie van een punt in het vlak of in een driedimensionale ruimte te specificeren. De cartesiaanse coördinaten of rechthoekig coördinatensysteem van een punt zijn een paar getallen (in twee dimensies) of een triplet van getallen (in drie dimensies) die getekende afstanden vanaf de coördinatenas specificeerden. Eerst moeten we een coördinatensysteem begrijpen om onze richtingen en relatieve positie te definiëren. Een systeem dat wordt gebruikt om punten in de ruimte te definiëren door richtingen (as) en een referentiepositie (oorsprong) vast te stellen. Een coördinatensysteem kan rechthoekig of polair zijn.
Net zoals punten op de lijn één-op-één kunnen worden geplaatst met de reële getallenlijn, zo kunnen punten in het vlak één-op-één worden geplaatst met paren reële getallenlijnen door twee coördinaatlijnen te gebruiken. Om dit te doen, construeren we twee loodrechte coördinatenlijnen die elkaar snijden bij hun oorsprong; voor het gemak. Wijs een reeks gelijkmatige schaalverdelingen toe aan de x- en y-assen, beginnend bij de oorsprong en in beide richtingen, links en rechts (x-as) en op en neer (y-as) punt langs elke as kan worden vastgesteld. We maken een van de getallenlijnen verticaal met de positieve richting naar boven en de negatieve richting naar beneden. De andere getallenlijnen horizontaal met de positieve richting naar rechts en de negatieve richting naar links. De twee getallenlijnen worden coördinaatassen genoemd; de horizontale lijn is de x-as, de verticale lijn is de y-as en de coördinaatassen vormen samen het cartesiaanse coördinatensysteem of een rechthoekig coördinatensysteem. Het snijpunt van de coördinaatassen wordt aangegeven met O en is de oorsprong van het assenstelsel. Zie figuur 1.
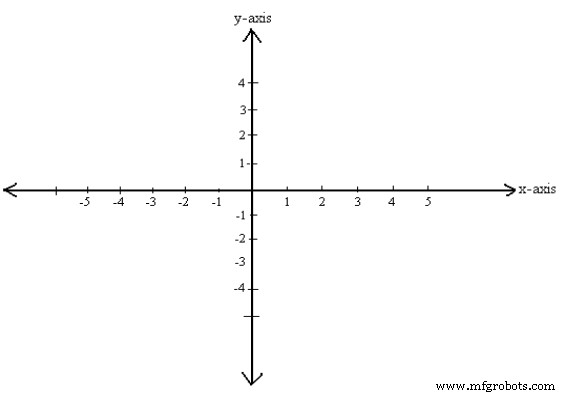
Figuur 1
Het is eigenlijk twee reële getallenlijnen bij elkaar, de ene gaat van links naar rechts en de andere gaat van boven naar beneden. De horizontale lijn wordt de x-as genoemd en de verticale lijn wordt de y-as genoemd.
De oorsprong
Het punt (0,0) krijgt de speciale naam “The Origin” en soms de letter “O”.
Reële getallenlijn
De basis van dit systeem is de reële getallenlijn die met gelijke intervallen is gemarkeerd. De as is gelabeld (X, Y of Z). Eén punt op de lijn wordt aangeduid als de oorsprong. Cijfers aan de ene kant van de lijn zijn gemarkeerd als positief en die aan de andere kant als negatief. Zie afbeelding 2.
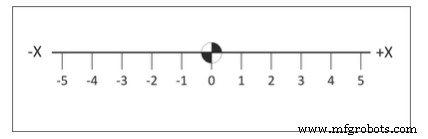
Afbeelding 2. X-as getallenlijn
Cartesiaanse coördinaten van het vliegtuig
Een vlak waarin een rechthoekig coördinatenstelsel is ingevoerd is een coördinatenvlak of een x-y-vlak. We zullen nu laten zien hoe u een één-op-één overeenkomst kunt vaststellen tussen punten in een coördinatenvlak en paren van reële getallen. Als A een punt in een coördinatenvlak is, dan trekken we twee lijnen door A, één loodrecht op de x-as en één loodrecht op de y-as. Als de eerste lijn de x-as snijdt op het punt met coördinaat x en de tweede lijn de y-as snijdt op het punt met coördinaat y, dan associëren we het paar (x,y) met de A (zie figuur 2). Het getal a is de x-coördinaat of abscis van P en het getal b is de y-coördinaat of ordinaat van p; we zeggen dat A het punt is met coördinaat (x,y) en duiden het punt aan met A(x,y). Het punt (0,0) krijgt de speciale naam “The Origin” en soms de letter “O”.
Abscis en ordinaat:
De woorden "Abscissa" en "Ordinaat" ... het zijn slechts dexandywaarden:
- Abscisse:de horizontale (“x”) waarde in een paar coördinaten:hoe ver is het punt.
- Ordinate:de verticale (“y”) waarde in een paar coördinaten:hoe ver het punt omhoog of omlaag is.
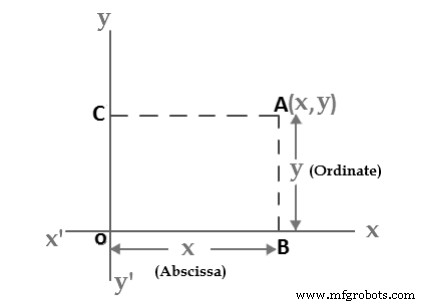
Figuur 3
Negatieve waarden van X en Y:
De reële getallenlijn, je kunt ook negatieve waarden hebben.
Negatief:begin bij nul en ga in de tegenovergestelde richting; Zie afbeelding 4
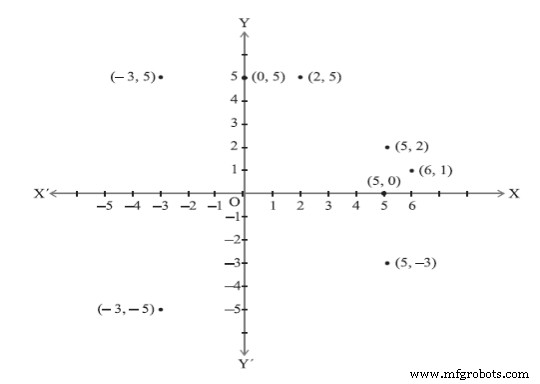
Figuur 4
Dus voor een negatief getal:
- goleftfor x
- goed voor jou
ga links langs de x-as 3 en ga dan 5 omhoog in de y-as. (Kwadrant II x is negatief, y is positief)En(-3,-5)betekent:
links langs de x-as 3 en dan naar beneden 5 in de y-as. (Kwadrant III x is negatief, y is negatief) Markeer met behulp van cartesiaanse coördinaten een punt in een grafiek hoe ver en hoe ver omhoog is; Zie figuur 5. Het punt (12,5) is 12 eenheden langs de x-as en 5 eenheden omhoog op de y-as.
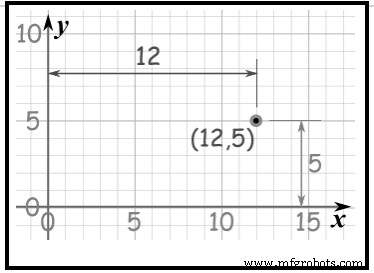 Afbeelding 5X- en Y-as:
Afbeelding 5X- en Y-as: 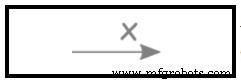 De horizontale lijn wordt de x-as genoemd en de verticale lijn wordt de y-as genoemd; beide lijnen lopen door nul (Origin, (0,0)).
De horizontale lijn wordt de x-as genoemd en de verticale lijn wordt de y-as genoemd; beide lijnen lopen door nul (Origin, (0,0)).  De horizontale lijn wordt de x-as genoemd en de verticale lijn wordt de y-as genoemd; beide lijnen lopen door nul (Origin, (0,0)). Zet ze samen in een grafiek … Zie figuur 6
De horizontale lijn wordt de x-as genoemd en de verticale lijn wordt de y-as genoemd; beide lijnen lopen door nul (Origin, (0,0)). Zet ze samen in een grafiek … Zie figuur 6 
Figuur 6
Het is eigenlijk een set van twee reële getallenlijnen.
As:De referentielijn van waaruit afstanden worden gemeten.
Voorbeeld:
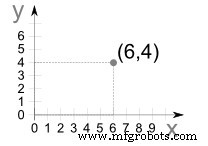 Point(6,4)is
Point(6,4)is Ga langs de x-richting 6 eenheden en ga vervolgens 4 eenheden omhoog in de richting en vervolgens "plot the dot".
En u kunt onthouden welke as welke is door:
De coördinaten worden altijd in een bepaalde volgorde geschreven:
- eerst de horizontale afstand,
- dan de verticale afstand.
Besteld paar:
De cijfers worden gescheiden door een komma en er worden haakjes als volgt om het geheel gezet: (7,4)
Voorbeeld:(7,4) betekent 7 eenheden naar rechts (x-as) en 4 eenheden omhoog (y-as)
Cartesiaanse coördinaten van driedimensionale ruimte
In driedimensionale ruimte (xyz-ruimte), loodrecht georiënteerd op het xy-vlak. De z-as gaat door de oorsprong van het xy-vlak. Coördinaten worden bepaald volgens de oost-west voor x-as noord-zuid voor y-as, en omhoog-omlaag voor de z-as verplaatsingen vanaf de oorsprong. Het cartesiaanse coördinatensysteem is gebaseerd op drie onderling loodrechte coördinaatassen:de x-as, zij-as en dez-as, zie figuur 6 hieronder. De drie assen snijden elkaar in het punt dat de oorsprong wordt genoemd. Je kunt je voorstellen dat de oorsprong het punt is waar de muren in de hoek van een kamer de vloer raken. De x-as is de horizontale lijn waarlangs de muur links van je en de vloer elkaar kruisen. Zij-as is de horizontale lijn waarlangs de muur rechts van je en de vloer elkaar kruisen. De z-as is de verticale lijn waarlangs de muren elkaar snijden. De delen van de lijnen die je ziet terwijl je in de kamer staat, zijn het positieve deel van elk van de assen. Het negatieve deel van deze assen zou de voortzetting zijn van de lijnen buiten de kamer.
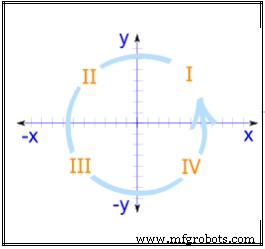
Afbeelding 7. 3D Cartesiaans coördinatensysteem
Driedimensionale Cartesiaanse coördinaatassen. Een weergave van de drie assen van het driedimensionale cartesiaanse coördinatenstelsel. De positievex-as, positievey-as en positievez-as zijn de zijden met het label byx,yandz. De oorsprong is het snijpunt van alle assen. De tak van elke as aan de andere kant van de oorsprong (de niet-gelabelde kant) is het negatieve deel.
Als het gaat om 3-dimensionale beweging, is het opzetten van een geschikt coördinatensysteem. Het meest ongecompliceerde type coördinatensysteem wordt een cartesiaans systeem genoemd. Een cartesiaans coördinatenstelsel bestaat uit drie onderling loodrechte assen, de X-, Y- en Z-assen. Volgens afspraak is de oriëntatie van deze assen zodanig dat wanneer de wijsvinger, de middelvinger en de duim van de rechterhand zodanig zijn geconfigureerd dat ze onderling loodrecht staan, de wijsvinger, de middelvinger en de duim kunnen worden uitgelijnd langs respectievelijk de X-, Y- en Z-assen. Zo'n coördinatenstelsel wordt rechtshandig genoemd. Zie figuur 7. Het snijpunt van de drie coördinaatassen wordt de oorsprong van het coördinatenstelsel genoemd.
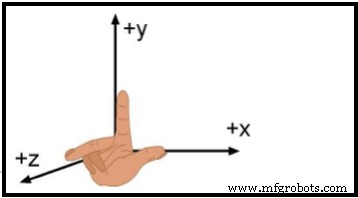
Figuur 8. Het rechtshandige cartesiaanse systeem
De cartesiaanse coördinaten van een punt in drie dimensies zijn een triplet van getallen (x,y,z). De drie getallen, of coördinaten, specificeren de ondertekende afstand vanaf de oorsprong langs respectievelijk de x-, y- en z-assen. Ze kunnen worden gevisualiseerd door de doos te vormen met randen evenwijdig aan de coördinatenas en tegenoverliggende hoeken bij de oorsprong en het gegeven punt.
De punten kunnen nu worden gedefinieerd in een driedimensionaal ruimtevolume. Dit maakt het mogelijk om punten in drie dimensies vanaf de oorsprong te definiëren. De cartesiaanse coördinaten (x,y,z) van een punt in drie dimensies specificeren de getekende afstand vanaf de oorsprong langs respectievelijk de x,y, enz-assen. Punten op de Z-as worden de derde invoer bij het definiëren van coördinaatlocaties.
Gezien de bovenstaande analogie in de hoek van de kamer, zouden we de Cartesiaanse coördinaten van het punt bovenaan je hoofd als volgt kunnen vormen. Stel je voor dat je vijf meter lang bent op de z-as, en dat je twee meter vanaf de oorsprong langs de x-as loopt, dan naar links gaat en evenwijdig aan de z-as vier meter de kamer in loopt. De cartesiaanse coördinaten van het punt bovenaan je hoofd zouden (2,4,5) zijn.
Een notatie van (2,4,5) komt bijvoorbeeld overeen met de waarde van X2, Y4 en Z5. Zie figuur 8.
3 afmetingen
Cartesiaanse coördinaten kunnen worden gebruikt voor het lokaliseren van punten in 3 dimensies, zoals in dit voorbeeld:

Figuur 9. Het punt (2, 4, 5 ) wordt weergegeven in driedimensionale cartesiaanse coördinaten.
Kwadranten
De coördinaatassen verdelen het vlak in vier delen, kwadranten genoemd (zie figuur 9). De kwadranten zijn tegen de klok in genummerd, beginnend vanaf rechtsboven, gelabeld I, II, III en IV met asaanduidingen zoals weergegeven in de onderstaande afbeelding.
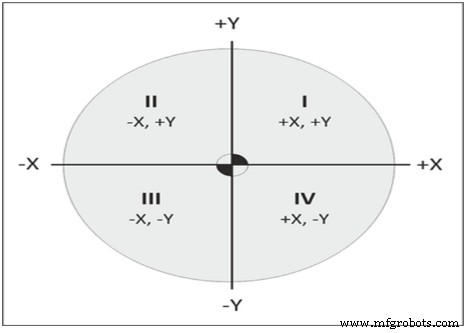
Figuur 10
Vier kwadranten:
Als we negatieve waarden opnemen, verdelen de x- en y-assen de ruimte in 4 stukken:
Kwadranten I, II, III en IV
(Ze zijn tegen de klok in genummerd)

InQuadrant I:zowel x als y zijn positief
InQuadrant II :x is negatief (y is nog steeds positief)
InQuadrant III:zowel x als y zijn negatief
InQuadrant IV :x is weer positief, terwijl y negatief is
| Kwadrant | X (horizontaal) | Y (verticaal) | Voorbeeld |
| Ik | Positief | Positief | (3,2) |
| II | Negatief | Positief | (-5, 2) |
| III | Negatief | Negatief | (-2, -1) |
| IV | Positief | Negatief | (2, -5) |
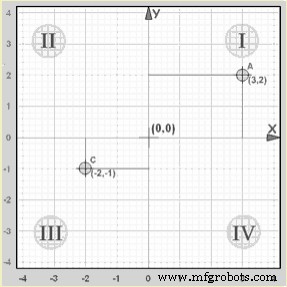
Voorbeeld:het punt "A" (3,2) is 3 eenheden langs de x-as en 2 eenheden omhoog langs de y-as.
Zowel x als y zijn positief, dus dat punt ligt in "Kwadrant I"
Voorbeeld:het punt "C" (-2,-1) is 2 eenheden langs de x-as in de negatieve richting en 1 eenheid langs de y-as in de negatieve richting.
Zowel x als y zijn negatief, dus dat punt ligt in “Kwadrant III”
Afmetingen:1, 2, 3 en meer ...
1. TheReal Number Linekan alleen gaan:
- links-rechts
- dus elke positie heeft maar één nummer nodig
2. Cartesiaanse coördinaten kunnen gaan:
- links-rechts, en
- omhoog-omlaag
- dus elke positie heeft twee cijfers nodig
3. 3 dimensies
- links-rechts,
- omhoog, en
- vooruit-achteruit
EENHEIDSTEST
1. Wat is CNC?
2. Beschrijf het cartesiaanse coördinatensysteem.
3. Wat is de oorsprong?
4. Hoe heet de horizontale lijn?
5. Hoe heet de verticale lijn?
6. Beschrijf de echte getallenlijn.
7. Leg Abscissa uit en Ordinaat.
8. Wat zijn de representaties van de drie assen van het driedimensionale cartesiaanse coördinatensysteem.
9. De coördinaatassen verdelen het vlak in vier delen, hoe heet dat?
10. In kwadrant IV zijn de X-assen en de Y-assen wat?
Industriële technologie
- CNC-machinegereedschap
- Hoe gebruik je een CNC-freesmachine?
- Hoe de nauwkeurigheid van CNC-bewerkingsmachines te verbeteren
- Draaibankmachinebewerkingen en draaibanksnijgereedschappen
- Wat is een schaafmachine? - Definitie, onderdelen en typen
- Hoe AI en machine learning van invloed zijn op CNC-bewerkingen
- EDM- en CNC-machinebrandbeveiliging:uw opties vergelijken
- 22 Unit 5:CNC-bewerking
- Nauwkeurigheid en positionering van CNC-bewerkingsmachines maximaliseren
- Onderdelen en elementen van CNC-machinesystemen
- G-codes en M-codes voor CNC-machines – CNC-frezen en -draaibank



