Analytisch model voor de maximale kanaaltemperatuur in Ga2O3-MOSFET's

Methoden en modelontwikkeling

Het analytische model voor T _max in Ga₂ O₃ MOSFET's worden voorgesteld op basis van de structuur die wordt getoond in Fig. 1. De belangrijkste parameters van de structuur worden vermeld in tabel 1. Er is zelfs aangetoond dat de Joule-verwarming geconcentreerd is aan de afvoerrand van de poort in Ga₂ O₃ MOSFET's [13]. Om het model eenvoudig te maken, wordt aangenomen dat het verwarmingseffect van de poort uniform is [12] en volledig door het poortoxide kan dringen vanwege de verwaarloosbare dikte. Verschillende substraatmaterialen onder Ga₂ O₃ kanalen worden in dit model overwogen, zoals bulk Ga₂ O₃ en hoge κ materialen, gericht op de haalbaarheid en compatibiliteit van het bord. Het apparaat wordt dus gezien als een probleem met twee lagen. Het substraat komt in contact met een ideaal koellichaam, zodat het bodemoppervlak isotherm is en de temperatuur gelijk is aan die van de omgevingstemperatuur (T _amb , 300 K standaard). Adiabatische randvoorwaarden werden opgelegd aan een ander oppervlak van de constructie. Deze randvoorwaarden kunnen worden samengevat als [14, 16]

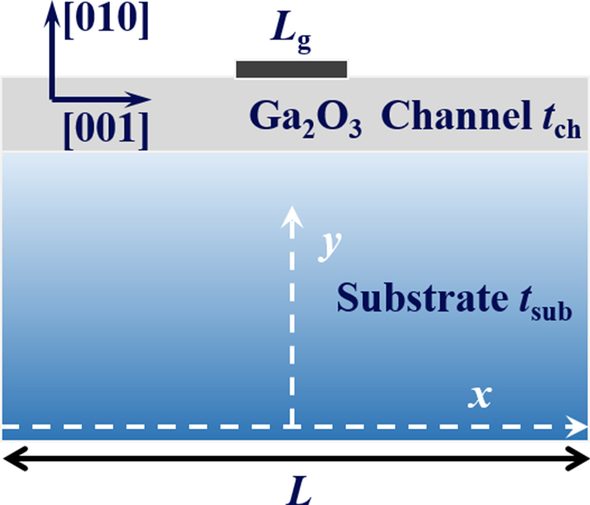
Het schematische diagram van Ga₂ O₃ MOSFET

waar P , T en κ _j duiden de vermogensdissipatiedichtheid, temperatuur en thermische geleidbaarheid van [010] richting voor Ga₂ O₃ , respectievelijk. Benadrukt moet worden dat de eenheid van P is W/mm in dit papier.

De κ waarde van Ga₂ O₃ , een van de belangrijkste parameters voor de thermische eigenschappen van materiaal, speelt een belangrijke rol bij de diffusie van het verwarmingseffect en de nauwkeurigheid van het model. Dat wil zeggen, een zorgvuldige beschrijving van κ waarde is vereist vanwege de ernstige anisotropie en temperatuurafhankelijkheid [17]. In het algemeen is de afhankelijkheid van κ van Ga₂ O₃ op temperatuur (T ) langs twee verschillende kristaloriëntaties ([001] en [010]) wordt gegeven door

De vergelijkende studie van T _max op verschillende P werd uitgevoerd door COMSOL Multiphysics, rekening houdend met constante en realistische κ , respectievelijk. Dat vonden we bij een P van 1 W/mm, T _max waarden van respectievelijk 533 K en 622 K worden verkregen (niet getoond). Daarom is het heel noodzakelijk om rekening te houden met de effecten van T en kristallografische richting op de κ van Ga₂ O₃ in het model.

Het temperatuurgedrag wordt bepaald door de warmtegeleidingsvergelijking. De warmtegeleidingsvergelijking bij stationaire toestand in Ga₂ O₃ domein is

waar κ _x geeft de thermische geleidbaarheid van [001] richting voor Ga₂ O₃ . De niet-lineaire warmtegeleidingsvergelijking kan worden opgelost door de transformatie van Kirchhoff toe te passen. De toepassing van de transformatie van Kirchhoff kan echter beperkt zijn vanwege de zeer anisotrope κ in Ga₂ O₃ , die strikt genomen alleen geldig is voor materialen met isotrope κ [14]. Gezien de bovenstaande beperking, moet men κ . niet overwegen _x en κ _j twee onafhankelijke variabelen zijn. Afbeelding 2 toont de relatie tussen de thermische weerstand, d.w.z. 1/κ , en T voor richtingen van [001] en [010] over een grote T bereik, respectievelijk. Het is te zien dat 1/κ _j kan worden vervangen door 1/(cκ _x ) en c wordt gekozen om gelijk te zijn aan 1,64. Bijgevolg, vgl. (6) kan worden omgezet in de volgende vergelijking:

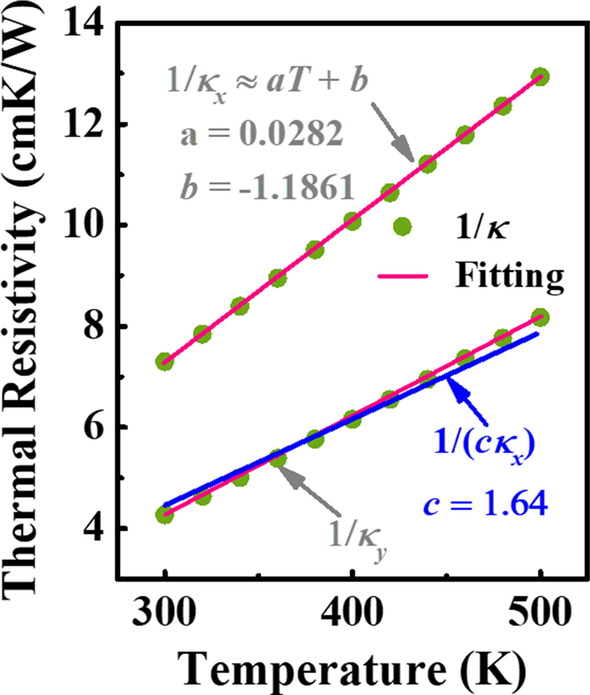
De relatie tussen de thermische weerstand en T voor aanwijzingen van [001] en [010]. Groene symbolen en rode lijnen geven respectievelijk werkelijke en aangepaste waarden aan. Blauwe lijn vertegenwoordigt de hypothese van 1/κ _j ≈ 1/(cκ _x ), waarbij c = 1,64

Gebaseerd op de voorgaande benaderingen van κ _x en κ _j , kan de transformatie van Kirchhoff zonder enige beperking worden toegepast. Bovendien kan ook worden gezien dat het omgekeerde van κ zal naar verwachting evenredig zijn met T. Dus, om de computationele complexiteit te verminderen, de uitdrukking van 1/κ _x kan worden vereenvoudigd als 1/κ _x = aT + b , zoals weergegeven in Afb. 2. De reden voor het gebruik van a , b en c is gewoon gemak bij het schrijven van de volgende vergelijkingen.

Door toepassing van de transformatie van Kirchhoff en de methode van scheiding van variabelen, wordt de uitdrukking van T _max kan worden afgeleid als

waar

Er moet op worden gewezen dat S is een convergente oneindige reeks en de geschatte waarde die gemakkelijk kan worden verkregen, wordt bij de berekening gebruikt in plaats van de werkelijke waarde.

In het geval van Ga₂ O₃ MOSFET's met hoge κ substraten, kan de transformatie van Kirchhoff niet direct theoretisch worden toegepast. Om de transformatie geldig te laten zijn, moeten de randvoorwaarden isotherm zijn (constante T oppervlak), of een vaste warmtestroomdichtheid hebben. Vanwege de verschillende κ van Ga₂ O₃ en substraatmateriaal, aan beide randvoorwaarden wordt niet volledig voldaan bij de Ga₂ O₃ /substraat-interface. Aangezien de κ van Ga₂ O₃ is veel lager dan hoog κ substraat, een hypothese, de isotherme interface tussen de Ga₂ O₃ en het substraat, wordt ingebracht. Deze hypothese is behulpzaam bij het afleiden van de uitdrukking T _max en de geldigheid ervan zal later worden gecontroleerd. In dit geval is de thermische weerstand (R _TH ) van hoge κ substraat, een verhouding van het verschil tussen de T _int en T _amb en de PW , d.w.z. R _TH = (T _int —T _amb ) / (PW ), kan worden berekend als R _TH = LW /(κt _sub ), waarbij W is de breedte van het substraat [19]. Dus de uitdrukking van de temperatuur van Ga₂ O₃ /substraat-interface (T _int ) is

waar κ _sub is de thermische geleidbaarheid van heterogeen substraat, waarvan wordt aangenomen dat deze constant is. Bovendien moet erop worden gewezen dat de thermische grensweerstand tussen Ga₂ O₃ en heterogene substraten zijn niet in het model opgenomen. Daarom, met de hulp van Vgl. (8), de uitdrukking van T _max voor Ga₂ O₃ MOSFET's met heterogeen substraat kunnen worden afgeleid als

waar

Resultaten en discussie

De validiteit van het analytische model voor de T _max in Ga₂ O₃ MOSFET's werden in deze sectie systematisch geverifieerd, rekening houdend met zowel het natuurlijke substraat als de tegenhanger met een hogere thermische geleidbaarheid. De beste manier om de validiteit van een model te testen is aan de hand van experimentele gegevens. Sommige belangrijke geometrische parameters konden echter niet worden gevonden in experimentele literatuur, zoals t _sub en L in ref. [12]. Daarom wordt eindige-elementensimulatie, een van de meest nauwkeurige middelen, gebruikt om ons model te verifiëren. Afbeelding 3 toont de afhankelijkheid van T _max over vermogensdichtheid P verkregen uit zowel COMSOL Multiphysics als analytisch model, voor Ga₂ O₃ MOSFET met natuurlijk substraat. Er wordt rekening gehouden met verschillende belangrijke parameters, waaronder apparaatlengte L , substraatdikte t _sub , en omgevingstemperatuur T _amb . Zoals weergegeven in Afb. 3a, is de T _max wordt natuurlijk verhoogd met de verhoogde vermogensdichtheid en de toenamesnelheid wordt verhoogd met de kleinere L . Dit wordt toegeschreven aan het apparaat met een grotere L zorgt voor warmteafvoer van het actieve gebied en daarom is de algehele temperatuur lager dan die met kleinere L op dezelfde P [11]. Dat wil zeggen, het is R _TH , de helling van krommen, is kleiner dan die van laatstgenoemde. Bovendien, aangezien de κ van Ga₂ O₃ zal afnemen met de toename van de algehele temperatuur, de R _TH zal ook langzamer toenemen dan dat met kleinere L bijgevolg, wat duidelijk is in figuur 3a [19]. Evenzo is het onderzoek naar de afhankelijkheid van T _max op t _sub werd uitgevoerd, zoals geïllustreerd in figuur 3b. Opgemerkt wordt dat de trend van T _max met betrekking tot P is hetzelfde als die in figuur 3a. Het dunnere substraat produceert altijd de verminderde stijging van T _max over de grotere vermogensdichtheid, wat begrijpelijk is dat hoe dunner het substraat, hoe lager de algehele temperatuur, hoe kleiner R _TH en de toenamesnelheid, net als de analyse in figuur 3a. Figuur 3c vergelijkt de invloed van T _amb op T _max als P neemt toe. Het is duidelijk dat het verschil tussen twee curven langzaam toeneemt, wat anders is dan die in figuur 3a, b. Gewoonlijk R _TH wordt gedomineerd door de geometrische parameters van het apparaat en de κ waarde van materiaal. Aangezien de structuur in dit geval echter vast is, is de toename van R _TH wordt alleen veroorzaakt door de afname van κ van Ga₂ O₃ . Aan de andere kant wordt een hoge mate van overeenstemming waargenomen voor het voorgestelde model, dat rekening houdt met de T - en richtingsafhankelijke relatie voor de κ van Ga₂ O₃ , wat het schaalbare karakter van het model bevestigt. Gemiddeld is het verschil tussen het voorgestelde model en de simulatie  < 1 K. De algehele uitstekende overeenstemming die wordt waargenomen, suggereert dat het voorgestelde model zeer effectief en nauwkeurig is.

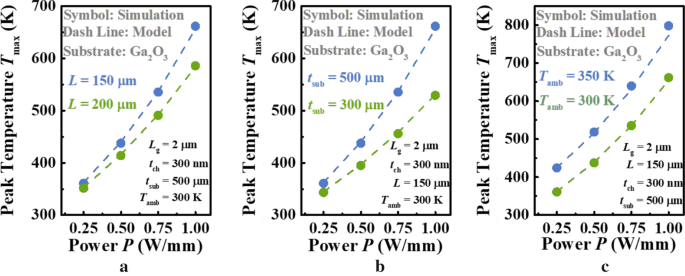
Afhankelijkheid van T _max op een de lengte van apparaat L , b de dikte van de substraatlaag t _sub , en c omgevingstemperatuur T _amb op ander vermogen P . Symbolen en lijnen geven respectievelijk de resultaten van het voorgestelde model en de simulatie aan

Evenzo, zoals weergegeven in Fig. 4, worden de vergelijkbare vergelijkingen herhaald voor Ga₂ O₃ MOSFET's op hoge κ substraat, SiC. Hier de stappen voor L en T _amb die we kiezen zijn groter dan die in Fig. 3, en de gevarieerde kanaaldikte t _ch wordt overwogen in plaats van t _sub in dit geval. Anders is het verschil tussen twee krommen van T _max met betrekking tot P in elke figuur zal niet te onderscheiden zijn, vanwege de efficiënte warmteafvoercapaciteit van SiC-substraat. De κ van SiC (3,7 Wcm ⁻¹ K ⁻¹ ) toegepast is een standaardparameter in COMSOL Multiphysics-software. Dankzij hoge κ van SiC, blijkt uit alle cijfers duidelijk dat de toename van T _max is ongeveer lineair als P neemt toe, wat betekent dat de invloed van de temperatuur op de R _TH van het apparaat is te verwaarlozen. Opgemerkt moet worden dat ons model deze lineaire relatie met succes kan beschrijven. Het is echter duidelijk dat de T _max berekend door het huidige model lager is dan die voorspeld door simulatie, en dit verschil is duidelijker naarmate het stroomverbruik toeneemt. Om dit mechanisme te tonen, gesimuleerde T _int worden geëxtraheerd met toenemend vermogen en vergeleken met berekende T _int door vgl. (10) zoals weergegeven in Fig. 5. Het blijkt dat de Joule-verwarming meer geconcentreerd wordt in het midden van het apparaat als P neemt toe. Er zijn 0,5 K en 4 K ΔT tussen het model en de simulatie op deze locatie wanneer P =0,25 en 1 W/mm, respectievelijk. Dit is de reden dat ons model T . niet nauwkeurig kan voorspellen _max . Daarom is een meer redelijke hypothese van T _int is nodig om in de toekomst een hogere nauwkeurigheid te verkrijgen. Niettemin, de T _max wordt door het model voorspeld dat het slechts  < 4 K lager is dan dat door simulatie, zelfs bij een vermogensdissipatiedichtheid van 1 W/mm. Dat wil zeggen, hoewel de hypothese van uniforme T _int inconsistent is met de feiten, kan ons model een schatting geven van T _max met voldoende nauwkeurigheid.

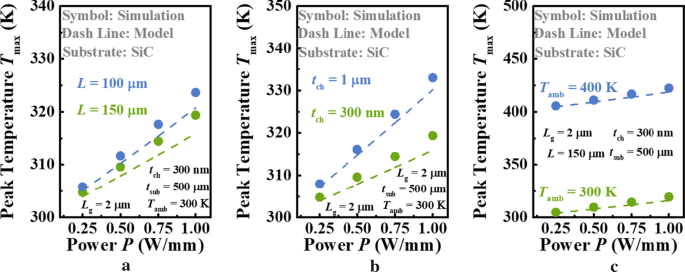
Afhankelijkheid van T _max van Ga₂ O₃ MOSFET's met SiC-substraat op a de lengte van apparaat L , b de dikte van Ga₂ O₃ laag t _ch , en c omgevingstemperatuur T _amb op ander vermogen P . Symbolen en lijnen geven respectievelijk de resultaten van het voorgestelde model en de simulatie aan

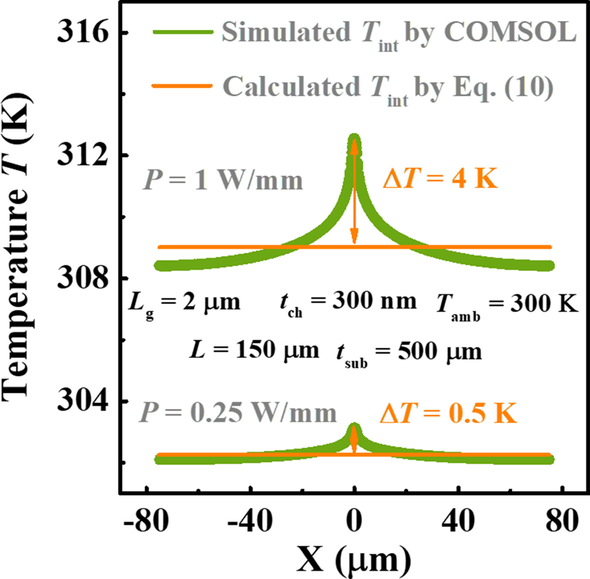
Vergelijking van T _int tussen gesimuleerd en berekend door Vgl. (10) op verschillende P