Waarneming van extrinsiek foto-geïnduceerd inverse spin-hall-effect in een GaAs/AlGaAs tweedimensionaal elektronengas
Abstract
Het inverse spin Hall-effect dat wordt veroorzaakt door circulair gepolariseerd licht is waargenomen in een tweedimensionaal elektronengas van GaAs/AlGaAs. De spin-dwarskracht is bepaald door de foto-geïnduceerde inverse spin Hall-effect (PISHE) stroom aan een theoretisch model te passen. De PISHE-stroom wordt ook gemeten bij verschillende lichtsterktes en verschillende lichtvlekprofielen, en alle meetresultaten komen goed overeen met de theoretische berekeningen. We meten ook de PISHE-stroom bij verschillende temperaturen (d.w.z. van 77 tot 300 K). De temperatuurafhankelijkheid van de PISHE-stroom geeft aan dat het extrinsieke mechanisme een dominante rol speelt, wat verder wordt bevestigd door de zwakke afhankelijkheid van de PISHE-stroom van de kristaloriëntatie van het monster.
Achtergrond
Spintronica heeft veel aandacht getrokken vanwege zijn potentiële toepassingen in de informatietechnologie en vanwege het onthullen van fundamentele vragen over de fysica van elektronenspin in gecondenseerde materie [1-4]. Het spin Hall-effect (SHE) en het omgekeerde Onsager-effect, het inverse spin Hall-effect (ISHE), spelen een belangrijke rol in spintronica omdat ze een elektrische methode bieden om laadstroom om te zetten in spinstroom en vice versa, via spin-baankoppeling ( SOC) [2, 5-8]. De SHE en ISHE zijn uitgebreid bestudeerd in metaalfilms met zware elementen, zoals Pt, Ta, Py en IrMn, en de opkomende topologische isolatoren, zoals Bi2 Se3 en SnTe, vanwege hun sterke SOC [9-14]. Deze twee effecten worden ook waargenomen in halfgeleiders, zoals GaAs, ZnO, Si, Ge, GaN/AlGaN en GaAs/AlGaAs tweedimensionaal elektronengas [15-20].
De omzetting van spin-naar-laadstroom in halfgeleiders is een belangrijk punt, omdat het een weg opent om spintronica met elektronica te integreren [5]. Foto-geïnduceerde ISHE (PISHE) is onlangs in opkomst als een effectief experimenteel hulpmiddel om de ISHE in halfgeleiders te onderzoeken, waarbij gebruik wordt gemaakt van circulair gepolariseerd licht met een Gauss-verdeling om een spinstroom in halfgeleiders te introduceren en vervolgens de ISHE gebruikt om een laadstroom te genereren [ 2, 19–22]. De PISHE-stroom kan bij kamertemperatuur worden waargenomen en biedt een handige manier om de ISHE van halfgeleiders te onderzoeken zonder een magnetisch veld en ferromagnetische elementen te introduceren [20]. Bovendien effent de PISHE ook een manier om nieuwe soorten spin-fotonica-apparaten te ontwerpen [22]. De PISHE-stroom is waargenomen in GaN/AlGaN-, GaAs/AlGaAs- en MgZnO/ZnO-heterostructuren [2, 19, 20]. De afhankelijkheid van de PISHE-stroom van het lichtvermogen en het lichtprofiel is echter nog onbekend.
Er zijn twee mechanismen voor ISHE, namelijk intrinsiek en extrinsiek. Het intrinsieke mechanisme is alleen afhankelijk van de bandstructuur van het perfect geordende materiaal [7, 23, 24], afkomstig van Rashba [25-27] of Dresselhaus SOC [26], terwijl het extrinsieke mechanisme verwijst naar asymmetrische Mott-skew of side -sprong verstrooiing van onzuiverheden in een spin-baan gekoppeld systeem [16, 24, 28, 29]. Hoewel er veel onderzoeken zijn die het intrinsieke of extrinsieke mechanisme van ISHE onderzoeken, zijn de meeste theoretische werken, en zeer weinig ervaringsgerichte werken die zich op dit probleem richten [16, 27, 30-32], omdat het erg moeilijk is om deze twee te onderscheiden. mechanismen experimenteel.
In dit artikel onderzoeken we de PISHE-stroom in een GaAs/AlGaAs tweedimensionaal elektronengas (2DEG). Het blijkt dat de PISHE-stroom toeneemt met toenemende temperatuur, wat aangeeft dat de PISHE-stroom voornamelijk wordt gedomineerd door het extrinsieke mechanisme. Deze gevolgtrekking wordt verder bevestigd door de zwakke afhankelijkheid van de PISHE-stroom van de kristaloriëntatie van het monster. Daarnaast onderzoeken we ook de afhankelijkheid van de PISHE-stroom van het lichtvermogen en het lichtprofiel, wat heel goed overeenkomt met het theoretische model.
Methoden
Het experiment wordt uitgevoerd op een (001)-georiënteerd modulatie-gedoteerde GaAs/AlGaAs 2DEG-monster dat is gegroeid door middel van moleculaire bundelepitaxie (MBE) op een semi-isolerend GaAs-substraat. De elektronendichtheid en de Hall-mobiliteit van het monster worden gemeten als 5,18 × 10 11 cm −2 en 3,97 × 10 3 cm 2 V −1 s −1 bij kamertemperatuur resp. De mobiliteit van de 2DEG is een beetje laag vanwege de doping op de achtergrond, die in de orde van 10 15 ligt of 10 16 cm −3 , in het monster geïntroduceerd tijdens de monstergroei. Het monster wordt in de richting [110] en \([1\bar {1}0]\) gesplitst in een vierkant van 10 × 10 mm 2 . Twee paar ohmse contacten met een afstand van 8 mm in respectievelijk [110] en [100] richtingen, worden gemaakt door indiumafzetting en uitgegloeid bij ongeveer 420 °C in een stikstofatmosfeer.
Als stralingsbron wordt een diode-gepompte vastestoflaser met een golflengte van 1064 nm gebruikt. De laserstraal gaat door een chopper, een polarisator en een kwartgolfplaat en verlicht het monster uiteindelijk verticaal. Hier worden de polarisator en de roterende kwartgolfplaat gebruikt om de lichtheliciteit P te veranderen c =sin2φ van linkshandig (σ − , P c =− 1) naar rechtshandig (σ + , P c =+ 1) continu, waarbij φ is de hoek tussen de polarisatierichting van het invallende licht en de optische as van de kwartgolfplaat. De lichtvlek op het monster heeft een Gaussiaans profiel. De stroom wordt verzameld tussen de twee contacten in de richting [100] (of [110]) van het monster door een voorversterker en een lock-in-versterker met een referentiefrequentie van 229 Hz van de chopper. Afbeelding 1a illustreert de opstelling die wordt gebruikt om de PISHE-stroom te meten.
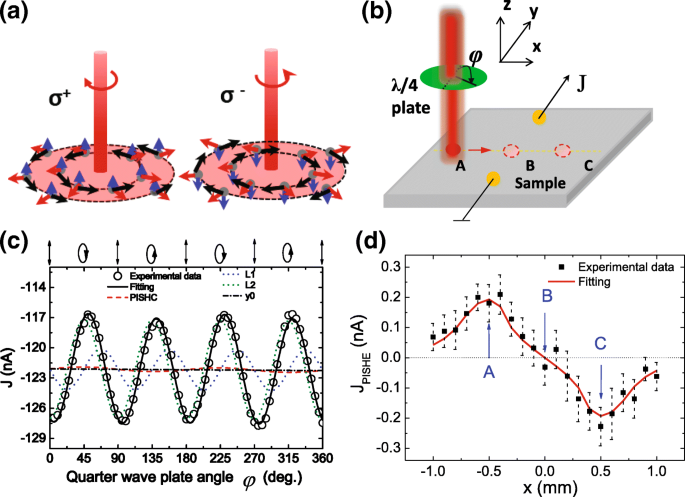
Methode om de PISHE-stroom te verkrijgen en de PISHE gemeten bij 300 K. a Illustratie van de beweging van spin-gepolariseerde elektronen onder de normale verlichting van linker circulaire polarisatie (σ + ) of rechtse circulaire polarisatie (σ − ) licht. De rode pijlen geven het stromen van elektronen aan, de blauwe pijlen geven de spinrichting van elektronen aan en de zwarte pijlen geven de spin-dwarskracht weer die op elektronen inwerkt. b De geometrie die wordt gebruikt om de PISHE-stroom te meten. c De fotostroom gemeten bij 300 K als functie van de fasehoek φ onder normale inval wanneer de lichtvlek wordt geïllustreerd in punt A. De ononderbroken lijn (zwart) is de fittingcurve met gebruik van Vgl. (1), de stippellijn (rood) vertegenwoordigt de PISHE-stroom en de blauwe en groene stippellijnen vertegenwoordigen de L 1 en L 2 onderdeel. De stippellijn geeft de achtergrondstroom aan J 1 . d De PISHE-stroom als functie van lichtvleklocaties gemeten bij 300 K
Voor vermogensafhankelijke metingen wordt het vermogen van het op het monster uitgestraalde licht gewijzigd van 250 naar 40 mW met behulp van verzwakkers. Om het profiel van de lichtvlek op het monster te veranderen, wordt een optische lens met verschillende brandpuntsafstanden gebruikt. Bij de temperatuurafhankelijke metingen wordt het monster op een optische cryostaat gemonteerd, waardoor de temperatuur kan variëren van 77 tot 300 K.
Om de relatieve verhouding van Rashba tot Dresselhaus SOC te verkrijgen, meten we de fotostroom die wordt geïnduceerd door circulair fotogalvanisch effect (CPGE) voor verschillende kristallografische richtingen, dwz dat de CPGE-stroom wordt verzameld in de richting [110] en [100] door respectievelijk de contacten, met het invallende vlak van licht loodrecht op de verbinding van de twee contacten. Voor de CPGE-meting wordt een vergelijkbare experimentele opstelling gebruikt als die gebruikt in de PISHE-meting, behalve dat het licht schuin uitstraalt op het middelpunt van de verbinding van de twee contacten langs [110] of [100] richtingen, en de invalshoeken variëren van − 40 tot 40°. De CPGE-stroom bij een bepaalde invalshoek wordt geëxtraheerd door de licht-polarisatie-toestandafhankelijke fotostroom J aan te passen verzameld langs de twee contacten tot de volgende vergelijking [33]:J =J CPGE sin2φ +L 11 sin4φ +L 22 cos4φ +J 11 . Hier, J CPGE is de CPGE-stroom, L 11 en L 22 zijn de fotostroom geïnduceerd door lineair gepolariseerd licht, en J 11 is de achtergrondstroom afkomstig van het fotovoltaïsche effect of Dember-effect [33].
Resultaten en discussie
Onder een belichting van circulair gepolariseerd licht met een Gauss-profiel, zullen spin-gepolariseerde dragers met een Gauss-verdeling in de ruimte worden gegenereerd in het onverzadigde absorptiegebied. Hierdoor ontstaat een diffuse spinstroom die in radiale richting vloeit. Als gevolg van het ISHE-effect ervaren de spin-gepolariseerde dragers vervolgens een "spin-dwarskracht" langs de tangentiële richting, wat leidt tot een transversale laadstroom, dwz een vortexstroom (genaamd PISHE-stroom), in de axiale richting [8, 20], zoals getoond in Fig. la. Omdat de polarisatiestatus van het licht verandert van linkse circulaire polarisatie (σ + ) naar de rechter circulaire polarisatie (σ − ), wordt de spinpolarisatie van elektronen veranderd van spin omhoog naar spin omlaag, wat leidt tot de omkering van de spindwarskracht en de PISHE-stroom. Aangezien de kwartgolfplaat roteert van 0 tot 180°, d.w.z. als de hoek φ wordt veranderd van 0 naar 180°, de polarisatietoestand van het licht wordt veranderd van verticaal lineaire polarisatie (bij 0°), naar linkse circulaire polarisatie (bij 45°), verticaal lineaire polarisatie (bij 90°), rechts circulaire polarisatie (bij 135°), en opnieuw verticaal lineaire polarisatie (bij 180°) achtereenvolgens, zoals getoond in het bovenste deel van Fig. 1c. Daarom, als de hoek φ wordt gewijzigd van 45 in 135°, wordt de PISHE omgekeerd, wat aangeeft dat de PISHE evenredig is met sin2φ . Het is vermeldenswaard dat, op een φ hoek van 0, 90 en 180° is het licht lineair gepolariseerd. Het lineair gepolariseerde licht zal ook fotostroom induceren vanwege het optische momentumuitlijningseffect [34], genaamd L 1 , of vanwege de anisotropie optische absorptie [35, 36], genoemd als L 2 . De stromingen L 1 en L 2 geïnduceerd door lineair gepolariseerd licht zijn evenredig met sin4φ en cos4φ , respectievelijk. Trouwens, een achtergrond fotostroom J 1 afkomstig van het fotovoltaïsche effect of het Dember-effect, dat onafhankelijk is van de polarisatietoestand van het licht. Dus, volgens hun verschillende afhankelijkheid van de hoek φ , kunnen we de PISHE-stroom extraheren door de experimenteel gemeten lichtpolarisatie-toestandsafhankelijke fotostroom J naar de volgende formule [8, 33]:
$$ J=J_{\text{PISHE}}\sin 2\varphi+L_{1}\sin 4\varphi+L_{2} \cos 4\varphi+J_{1}, $$ (1)waar J PICHE is de PISHE-stroom opgewekt door links circulair polarisatielicht, L 1 en L 2 zijn de fotostroom geïnduceerd door lineair gepolariseerd licht, en J 1 is de achtergrondstroom [19]. Opgemerkt moet worden dat de L 2 term is opgenomen in de passende vergelijking, d.w.z. Vgl. (1), vanwege de grote optische anisotropie die in het monster aanwezig is. De optische anisotropie kan worden veroorzaakt door anisotrope interfacestructuren [37], segregatie van atomen [38] of restspanning [39].
Om de ruimtelijke verdeling van de PISHE te verkrijgen, vegen we de laservlek van links naar rechts van de twee contacten langs hun middelloodlijn [zie Fig.1a]. Op elke plekpositie roteren we de kwartgolfplaat van 0 tot 360 ° en verkrijgen we de PISHE-stroom door Vgl. (1) naar de experimenteel gemeten lichtpolarisatie toestandsafhankelijke fotostroom J . Figuur 1b toont een typisch resultaat van fotostroom gemeten als functie van de fasehoek φ , wanneer de laserspot is vastgezet op x =− 0,5 mm, d.w.z. op punt A [zie figuur 1a]. De fotostroom wordt gemeten bij 300 K en verzameld langs de twee contacten in de richting [110]. De laservlek op het monster heeft een diameter van ongeveer 1,4 mm met een Gaussiaans profiel en een vermogen van 250 mW. De cirkels in Fig. 1b zijn de experimentele gegevens en de ononderbroken lijn is het passende resultaat volgens Vgl. (1). Het is te zien dat de experimenteel gemeten fotostroom periodiek fluctueert met het draaien van de kwartgolfplaat. Dit komt omdat de fotostroom een sommatie is van de PISHE-stroom, de fotostroom geïnduceerd door lineair gepolariseerd licht en de achtergrondstroom, en ze vertonen een verschillende afhankelijkheid van hoek φ . De stippellijn geeft de PISHE-stroom aan en de stippellijn geeft de achtergrondstroom aan. De blauwe en groene stippellijnen vertegenwoordigen de L 1 en L 2 component geïnduceerd door respectievelijk lineair gepolariseerd licht. Men kan zien dat de PISHE-stroom veel kleiner is dan die van de fotostroom die wordt opgewekt door lineair gepolariseerd licht.
De verkregen PISHE-stroom als functie van de plek wordt getoond in figuur 1c. Het is te zien dat, wanneer de laservlek van links naar rechts van de twee contacten wordt verplaatst, de PISHE-stroom van richting verandert. Wanneer de laserspot is gericht op het middelpunt van de twee contacten, is de PISHE-stroom bijna gelijk aan nul. Dit fenomeen kan kwantitatief worden verklaard door een vortexstroommodel geïnduceerd door foto-geïnduceerd inverse spin Hall-effect [20]. Specifiek, onder de straling van een laser met een Gaussiaans profiel G (r )=\(\frac {1}{\sqrt {2\pi }\sigma }\exp \left (-\frac {r^{2}}{2\sigma ^{2}}\right)\), er zal een spinstroom worden geïnduceerd die langs de radiale richting vloeit, wat kan worden uitgedrukt als j r =τ s D ∇r G (r ). Hier, D is de spindiffusiecoëfficiënt, τ s is de spin-relaxatietijd, r geeft de radiale richting aan, en σ geeft de verdelingsvariantie aan gerelateerd aan de volledige breedte op half maximum (FWHM) van de lichtintensiteit. Door het ISHE-effect zullen de spin-gepolariseerde dragers een spin-dwarskracht \(f(r)\propto j_{r}\times \hat {z}\) [20, 40] ervaren, die kan worden uitgedrukt als \( f(r)=-f_{0}r/\sigma ^{3}\exp \left (-\frac {r^{2}}{2\sigma ^{2}}\right)\). Hier, f 0 is de spin-dwarskrachtconstante geassocieerd met SOC van het materiaalsysteem. Het elektrische veld van de vortex \(\vec {E}\) kan worden bepaald door de circulaire elektromotorische kracht (EMF), die kan worden geschreven als \(\varepsilon (r_{0})=\frac {2\pi }{q }\int _{0}^{r_{0}} f(r)rdr\), via \(\oint \vec {E}(r_{0})\cdot d\vec {l}=\varepsilon ( r_{0})\). Hier, r 0 is de straal van de lichtvlek, en de integrale lus is langs de omtrek van de lichtvlek. Daarom hebben we
$$ \nabla\times \vec{E}(r_{0})=-\frac{f_{0}r}{q\sigma^{3}}\exp \left(-\frac{r^{2 }}{2\sigma^{2}}\rechts). $$ (2)Het is vermeldenswaard dat het kleine verschil tussen Vgl. (2) en dat gerapporteerd in [20] is omdat de genormaliseerde Gauss-functie in dit artikel is overgenomen, terwijl de niet-genormaliseerde Gauss-functie werd gebruikt in [20]. De f 0 in dit artikel is gelijk aan f 0 /σ gerapporteerd in [20]. De elektrische stroom tussen de twee contacten (genoemd als a en b , respectievelijk) kan worden uitgedrukt als
$$ {}I_{ab}\,=\,\frac{V_{ab}}{R_{ab}}\,=\,\frac{1}{R_{ab}}\!\int_{a} ^{b}\! \vec{E}\cdot d\vec{l}\,=\,\frac{1}{R_{ab}}\!\oint_{abo}\!\vec{E}\cdot d\vec{l }\,=\,\frac{1}{R_{ab}}\iint_{S}\nabla\times\vec{E} ds, $$ (3)waar V ab (R ab ) is de spanning (weerstand) tussen de contacten a en b , o is de oorsprong van de lichtvlek, en S geeft het driehoekige gebied van abo . aan . Er moet worden vermeld dat het verzadigde absorptiegebied, waarin de door het monster geabsorbeerde lichtintensiteit een constante is en de maximale absorptie van het monster bereikt, moet worden afgetrokken van de integraal van Vgl. (3). Dit komt door het feit dat de gradiënt van de foto-gegenereerde dragers nul is in dat gebied, en als resultaat zijn de spinstroom en de PISHE-stroom allemaal nul in het gebied.
Het is vermeldenswaard dat Vgl. (3) geldt alleen als de contacten a en b vallen onder de lichtvlek, omdat buiten de lichtvlek Vgl. (2) is niet meer geldig. Dus, rekening houdend met de relatie tussen de elektrische stroom buiten (J f ) en binnen (J e ) de plek, d.w.z. J f =\(J_{e}\exp \left (-\frac {l}{A\cdot L_{s}}\right)\) [41], we kunnen Vgl. (3) als:
$$ I_{ab}=\frac{1}{R_{ab}}\iint_{D}\nabla\times\vec{E}\cdot\exp \left(-\frac{l}{A\cdot L_ {s}}\rechts)ds. $$ (4)Hier, l is de afstand tussen de rand van de lichtvlek en de verbinding van de twee contacten, L s is de diffusielengte van elektronen, en A is een constante. Vergelijkingen gebruiken. (2) en (4) om de experimenteel gemeten PISHE-stroom te passen, kunnen we de spin-dwarskracht f verkrijgen 0 en de diffusielengte A ·L s . Het montageresultaat wordt in Fig. 1c weergegeven door een ononderbroken lijn. Men kan zien dat de experimentele gegevens goed passen bij het model. Bij de aanpassing worden de volgende experimenteel gemeten parameters gebruikt, σ =0,2 mm, L =4 mm, r 0 =0,7 mm, en R ab =15,5 k Ω . De spin dwarskracht f 0 /q van elektronen is aangepast om 6,8 × 10 −6 . te zijn N ·m/C bij 300 K, A ·L s is uitgerust om 2,8 × 10 −4 . te zijn m, en de straal van het verzadigde absorptiegebied is aangepast op 0,34 mm, wat aangeeft dat de verzadigde absorptieintensiteit van het licht I c komt overeen met ongeveer een vijfde van de maximale intensiteit I m , d.w.z. ik c =1/5 Ik m .
Om de afhankelijkheid van de PISHE-stroom van het lichtvermogen en van het lichtprofiel te onderzoeken, voeren we de PISHE-meting uit onder verschillende lichtsterkten en verschillende lichtprofielen. Figuur 2a, b toont de PISHE-stroom als functie van lichtvleklocaties onder verschillende lichtsterkten met een lichtvlekstraal van r 0 =1,5 mm en σ =0,5 mm en r 0 =1 mm en σ =0,3 mm, respectievelijk. De symbolen zijn de experimentele gegevens en de ononderbroken lijnen zijn de theoretische berekeningen volgens Vgl. (2) en (4). In de berekeningen worden dezelfde parameters gebruikt, behalve de lichtvlekparameters, aangenomen in Fig. 1c, d.w.z. f 0 /q =6,8 × 10 −6 N ·m/C, A ·L s =2,8 × 10 −4 m, R ab =15,5 k Ω , en ik c =1/5 Ik m . Hier, ik m is de maximale lichtintensiteit van licht bij een vermogen van 250 mW. Het is te zien dat de intensiteit van de PISHE-stroom toeneemt met het lichtvermogen, en onder het vermogen van 250 mW, de lichtvlek met grotere FWHM (d.w.z. grotere σ ) leidt tot een grotere PISHE-stroom. We kunnen ook zien dat, voor een lichtvlek met grotere FWHM, de piek van de PISHE-curve een grotere waarde van x zal hebben . Hier, x is de afstand tussen het middelpunt van de lichtvlek en het middelpunt van de verbinding van de twee contacten. Dit komt omdat de spinstroom en de resulterende PISHE-stroom evenredig zijn met de gradiënt van het lichtprofiel. Voor een betere vergelijking van de PISHE-stroom geïnduceerd door verschillende lichtvlekprofielen, vatten we de resultaten van Fig. 2a, b in Fig. 2c samen, dwz we vatten de afhankelijkheid van de piekwaarde van de PISHE-stroom van het excitatievermogen voor verschillende lichtvlekprofielen in Fig. 2c, waar de symbolen de experimentele gegevens aangeven, en de ononderbroken lijnen de theoretische berekeningsresultaten zijn. Men kan zien dat de experimentele resultaten zeer goed overeenkomen met de theoretische simulaties, wat het model bevestigt.
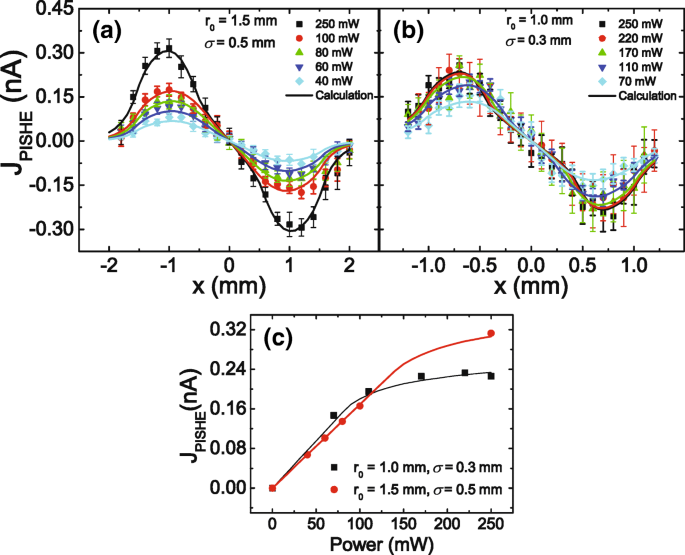
PISHE-stroom als functie van lichtvleklocaties onder verschillende lichtkracht. een , b PISHE-stroom opgewekt door een lichtvlek met Gauss-profiel met r 0 =1,5 mm en σ =0,5 mm en r 0 =1 mm en σ =0,3 mm, respectievelijk. c De variatie van de piekwaarde van de PISHE-stroom met het excitatievermogen, waarbij de symbolen en de ononderbroken lijnen respectievelijk de experimentele gegevens en de theoretische berekeningsresultaten zijn
Figuur 2c geeft aan dat, naarmate het vermogen toeneemt, de PISHE-stroom eerst monotoon toeneemt en dan geleidelijk verzadiging wordt. Het ontstaan van de verzadiging van de PISHE-stroom met lichtvermogen is te wijten aan de aanwezigheid van absorptieverzadiging bij hoog vermogen. Wanneer de maximale lichtintensiteit kleiner is dan de absorptieverzadigingsintensiteit, neemt de PISHE-stroom lineair toe met het lichtvermogen. Wanneer de maximale lichtintensiteit groter is dan de absorptieverzadigingsintensiteit, neigt de PISHE-stroom naar verzadiging met toenemend lichtvermogen. De invloed van de lichtvlekgrootte op de PISHE-stroom kan worden begrepen in het aspect van het effect van FWHM van de lichtvlek op de PISHE-stroom, omdat de lichtvlekgrootte en de FWHM met elkaar gecorreleerd zijn door lichtkracht. Specifiek geldt voor een bepaalde lichtkracht dat een grotere maat lichtvlek een grotere waarde van FWHM heeft. Bij een bepaald lichtvermogen, als de maximale lichtintensiteit kleiner is dan de absorptieverzadigingsintensiteit, kan een lichtprofiel met een kleinere FWHM (dwz een kleinere lichtvlek) een grotere PISHE-stroom genereren, omdat een kleinere FWHM zal resulteren in een grotere spin stroom; terwijl als de maximale lichtintensiteit groter is dan de absorptieverzadigingsintensiteit, een lichtprofiel met een kleinere waarde van FWHM zal leiden tot een kleinere PISHE-stroom. Dit is ook duidelijk te zien in Fig. 3, die de PISHE-stroom samenvat als een functie van lichtvleklocaties onder verschillende lichtprofielen. Het vermogen van de lamp is 250 mW. Het kan worden gezien dat, als de waarde van σ neemt toe van 0,2 tot 0,5 mm, de piekwaarde van de PISHE-stroom neemt monotoon af. Dit komt omdat er in het absorptie-verzadigde gebied geen spinstroom is en als gevolg daarvan geen PISHE-stroom wordt gegenereerd. Daarom levert het licht in het verzadigde absorptiegebied geen enkele bijdrage aan de PISHE-stroom. De inzet van Fig. 3 toont de verdeling van de lichtintensiteit voor verschillende Gauss-lichtprofielen. De stippellijn geeft de intensiteit van de absorptieverzadiging van het monster weer. De snijpunten tussen de stippellijn en de lichtintensiteitscurven geven de straal aan van de verzadigde absorptiegebieden, aangeduid als r s . Het licht binnen het cirkelvormige gebied met straal r s , wat wordt aangegeven door het schaduwgebied wanneer r 0 =1.5 en σ =0,5 mm, draagt niet bij aan de PISHE-stroom. Het kan worden gezien dat, voor een lichtvermogen van 250 mW, hoewel een lichtprofiel met een kleinere FWHM zal leiden tot een grotere spinstroom in het absorptie-onverzadigingsgebied, dit effect wordt overweldigd door de meer energie die wordt verspild in het absorptieverzadigingsgebied. Hierdoor is het lichtprofiel met een kleinere waarde van σ (d.w.z. σ =0,2 mm) genereert een kleinere waarde van PISHE dan die met grotere σ (d.w.z. σ =0,3 of 0,5 mm).
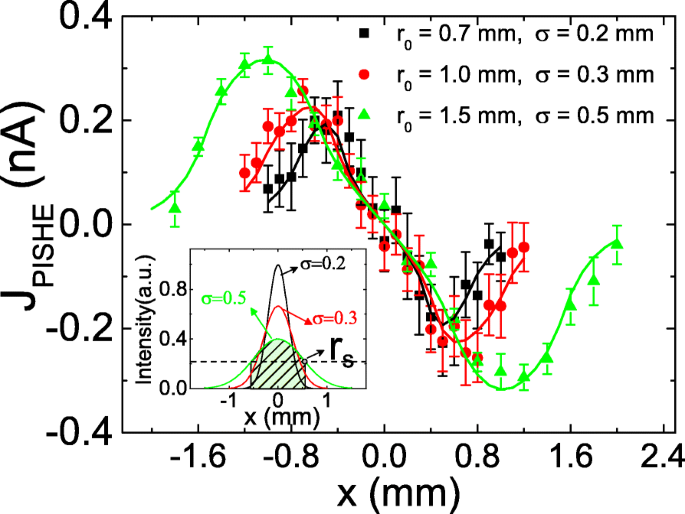
PISHE-stroom als functie van de locatie van de lichtvlek onder verschillende Gauss-lichtprofielen wanneer het lichtvermogen 250 mW is. De inzet toont de verdeling van de lichtintensiteit voor verschillende Gauss-lichtprofielen. De stippellijn geeft de absorptieverzadigingsintensiteit van het monster aan
Om het dominante mechanisme van de PISHE te onderzoeken, voeren we de PISHE-metingen uit bij verschillende temperaturen. Figuur 4a toont de PISHE-stroom als functie van de locatie van de lichtvlek gemeten bij 77, 130, 180 en 230 K. De laservlek heeft een Gaussiaans profiel met r 0 =0,7 mm en σ =0,2 mm, en het vermogen is 250 mW. De vierkanten geven de experimentele gegevens aan en de ononderbroken lijnen zijn de passende resultaten met behulp van vergelijkingen. (2) en (4). Het kan worden gezien dat de experimentele gegevens bij alle temperaturen allemaal goed door het model worden aangepast. Door de aanpassing kunnen we de spin-dwarskracht f . verkrijgen 0 /q , die wordt getoond in Fig. 4b, en de diffusielengte van elektronen A ·L s bij verschillende temperaturen. De stippellijn in figuur 4b is de richtlijn voor de ogen. Om de waarde van de parameter A te bepalen , moeten we de temperatuurafhankelijkheid van A . vergelijken ·L s naar de vorige resultaten van temperatuurafhankelijkheid van elektronendiffusielengte L s . Door onze waarde van A . aan te passen ·L s tot de waarde van L s verkregen in [42], kunnen we de constante A . bepalen 1,65 × 10 2 . zijn . De zeer goede overeenstemming van onze resultaten met eerdere resultaten getoond in Fig. 4c verifieert onze methode. Het is te zien dat de elektronendiffusielengte afneemt met toenemende temperaturen, wat voornamelijk kan worden toegeschreven aan de verbetering van de dragerverstrooiing door fononen [43].
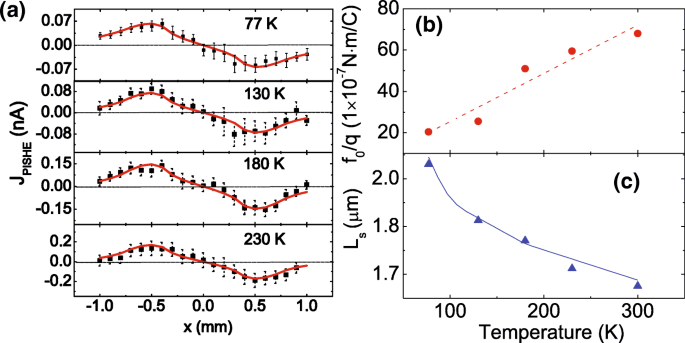
Temperatuurafhankelijkheid van de PISHE-stroom, spin-dwarskracht en elektronendiffusielengte van de GaAs/AlGaAs 2DEG. een Experimentele en modelleringsresultaten van de PISHE-stroom als functie van de lichtvleklocaties gemeten bij verschillende temperaturen. De ononderbroken vierkanten zijn de experimentele gegevens en de ononderbroken lijnen zijn de passende resultaten. b , c Spindwarskracht en elektronendiffusielengte als functie van de temperatuur, respectievelijk. De stippellijn in b is de gids voor de ogen, en de ononderbroken lijn in c is verkregen uit [42]
Verrassend genoeg is de spin dwarskracht f 0 /q van de 2DEG neemt monotoon toe met de toenemende temperatuur, wat een tegengestelde variatietrend op temperatuur laat zien voor de PISHE waargenomen in Au/InP hybride structuren [44]. Dit onverwachte fenomeen kan verband houden met het mechanisme van PISHE. Er zijn twee mechanismen voor de PISHE in halfgeleider 2DEG, namelijk intrinsieke en extrinsieke mechanismen. De eerste komt voornamelijk voort uit de bandstructuur en de laatste komt voort uit de asymmetrieën in verstrooiing voor op- en neerwaartse spins als gevolg van het SOC-effect in onzuiverheden [7, 16]. Voor een halfgeleider 2DEG van C 2v puntgroepsymmetrie, de spin-dwarskracht geïnduceerd door het intrinsieke mechanisme kan worden uitgedrukt als \(f_{0}=\frac {4m^{*2}\tau _{s}D}{\hbar ^{2}}\left (\alpha ^{2}+\beta ^{2}\right)\) [20, 40], waarbij \(\hbar \) de gereduceerde constante van Planck is, τ s is de spin-relaxatietijd, D is de spindiffusiecoëfficiënt, en α (of β ) is de Rashba (of Dresselhaus) constante die evenredig is met de sterkte van Rashba (of Dresselhaus) SOC. Voor een GaAs/AlGaAs 2DEG is de spin-relaxatietijd τ s is evenredig met T −1 [45]. Hier, T staat voor temperatuur. Voor de modulatie gedoteerde 2DEG is de sterkte van Rashba SOC veel groter dan die van Dresselhaus (zie de volgende discussie); als resultaat, de Rashba-constante α is veel groter dan de constante van Dresselhaus β . De spindiffusiecoëfficiënt D is evenredig met T −2 [46, 47]. De temperatuurafhankelijkheid van α kan worden uitgedrukt als a +b T , waar a en b zijn constanten, en a is ongeveer twee bestellingen groter dan b [48]. Dus, rekening houdend met de temperatuurafhankelijkheid van τ s , D , en α , we hebben f 0 ∝T −3 , wat suggereert dat de door het intrinsieke mechanisme geïnduceerde spin-dwarskracht zou moeten afnemen met toenemende temperaturen. Voor het extrinsieke mechanisme is de dwarskracht van de spin afhankelijk van de concentratie van geïoniseerde onzuiverheden, vooral voor extrinsieke zijsprongverstrooiing [49, 50]. Omdat er achtergronddotering in ons monster is en de ionisatie van onzuiverheden toeneemt met toenemende temperatuur, vindt sterkere asymmetrische verstrooiing voor spin-up en spin-down elektronen plaats naarmate de temperatuur stijgt, wat leidt tot grotere spin-dwarskracht bij toenemende temperatuur. Gegeven dat de spin dwarskracht f 0 waargenomen in ons experiment toeneemt met toenemende temperatuur, kan worden afgeleid dat de PISHE wordt gedomineerd door het extrinsieke mechanisme, waarbij de onzuiverheden voornamelijk worden geïntroduceerd door de achtergronddoping tijdens het groeiproces.
Om verder te bevestigen dat de PISHE inderdaad wordt gedomineerd door het extrinsieke mechanisme, meten we de ruimtelijke verdeling van de PISHE-stroom verzameld langs verschillende kristalrichtingen. Figuur 5a, b toont de ruimtelijke verdeling van de PISHE-stroom verzameld langs respectievelijk [110] en [100] kristalrichtingen. Om de invloed van de draaggolfmobiliteit en de draaggolfdichtheid in verschillende kristalrichtingen te elimineren, normaliseren we de PISHE-stroom met de overeenkomstige fotostroom J 0 onder een voorspanning van 0,3 V wanneer de contacten zich respectievelijk in de richtingen [110] en [100] bevinden. De metingen worden uitgevoerd bij kamertemperatuur onder een straling van 60 mW. De lichtvlekstraal r 0 is 1,0 mm, en σ bedraagt 0,3 mm. De symbolen geven de experimentele gegevens aan en de ononderbroken lijnen zijn de passende resultaten volgens vergelijkingen. (2) en (4). Het is te zien dat er geen duidelijk verschil is tussen de genormaliseerde PISHE-stroom die wordt verzameld langs [110] en [100] kristalrichtingen.
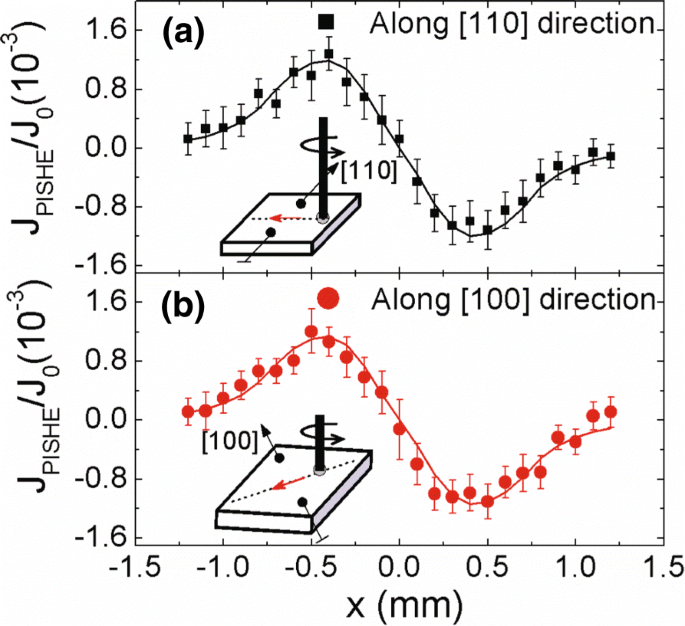
De genormaliseerde PISHE-stroom verzameld langs verschillende kristaloriëntaties. De PISHE-stroom wordt genormaliseerd door de fotostroom onder een voorspanning van 0,3 V. De ononderbroken symbolen zijn de experimentele gegevens en de ononderbroken lijnen zijn de theoretische passende resultaten. De inzetstukken tonen de schematische diagrammen voor de bijbehorende meetgeometrieën
Voor het intrinsieke mechanisme is de PISHE-stroom langs een bepaalde kristalrichting gerelateerd aan de spinsplitsing in die richting. Om kennis te krijgen van de anisotropie spinsplitsing in de GaAs/AlGaAs 2DEG, meten we de kristaloriëntatie-afhankelijkheid van de CPGE-stroom bij kamertemperatuur, dwz we hebben de CPGE-stroom gemeten wanneer de twee contacten langs [110] (of [100] ]) richting en het invallende vlak van licht ligt in [1\(\bar {1}\)0] (of [010]) richting, waarvan de meetresultaten worden weergegeven door vierkanten (of door cirkels) in Fig. 6 Het is vermeldenswaard dat bij het meten van de CPGE-stroom de lichtvlek zich in het midden van de verbinding van de twee contacten bevindt, waar de PISHE nul is volgens [20]. The CPGE current is also normalized by the corresponding photocurrent under a bias of 0.3 V to eliminate the influence of the carrier mobility and the carrier density in different crystal directions [51]. Then, we use the following equation to fit the normalized angle-dependent CPGE current to obtain the relative SOC strength along different crystal directions [21, 27]:
$$ \begin{aligned} J^{\lambda}/J_{0}=\frac{A_{\lambda}\sin \theta \cos^{2} \theta}{n\left[\cos\theta+\left(n^{2}-\sin^{2} \theta\right)^{1/2}\right]\left[n^{2}\cos \theta +\left(n^{2}-\sin^{2}\theta\right)^{1/2}\right]}. \end{aligned} $$ (5)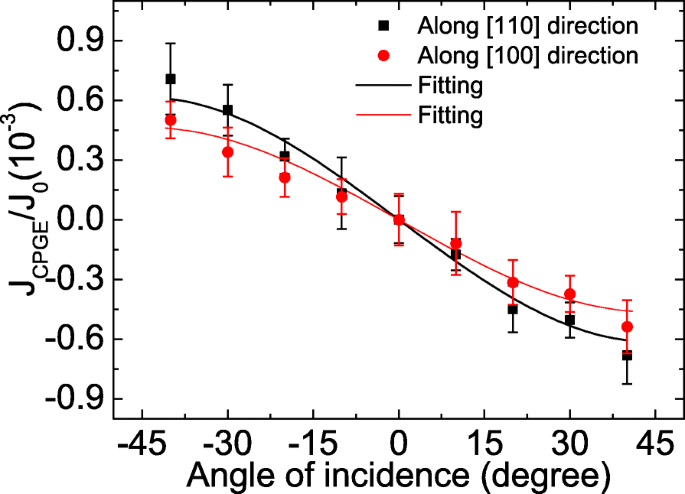
Incident angle dependence of the normalized CPGE current collected along different crystal orientations. The CPGE current is normalized by the photocurrent under a bias of 0.3 V. The solid symbols are the experimental data, and the lines are the fitting results according to Eq. (5)
Hier, θ is the angle of incidence, n is the refractive index of GaAs, and A λ is a constant proportional to the SOC constant. The fitting results are shown by the solid lines in Fig. 6. When the incident plane of light lies in [1\(\bar {1}\)0] direction and the CPGE current is collected along [110] direction, the corresponding A parameter, denoted as A [110] , is proportional to the sum of Rashba and Dresselhaus SOC, i.e., A [110] ∝α +β [51–53]. When the incident plane of light lies in [010] direction and the CPGE current is collected along [100] direction, the corresponding A parameter, denoted as A [100] , is proportional to the Rashba SOC, i.e., A [100] ∝α [51–53]. Thus, by the ratio of A [110] /A [100] , we can get the relative ratio of Rashba to Dresselhaus SOC, i.e., \(\beta /\alpha =\frac {A_{[110]}}{A_{[100]}}-1\) =0.32, which indicates that the spin splitting in the GaAs/AlGaAs 2DEG has crystal anisotropy [21]. Therefore, the intrinsic contribution to the PISHE should be sensitive to the crystal axis [16]. Specifically speaking, according to Eqs. (2) and (4), when the contacts are along [110] (or [100]) direction, the measured PISHE current is dominated by the inverse spin Hall current flowing nearly parallel to [110] (or [100]) direction since the PISHE current is a vortex current. If the intrinsic mechanism plays a dominant role in the 2DEG, the PISHE current collected along these two directions should be different. However, no marked difference is observed, which suggests that the extrinsic mechanism is dominant in the GaAs/AlGaAs 2DEG.
Conclusies
In conclusion, the PISHE current in a GaAs/AlGaAs 2DEG has been investigated in a temperature range of 77 to 300 K. The spin transverse force has been determined by fitting the PISHE current to a theoretical model. The dependence of the PISHE on the light power and on the light spot profiles has been investigated, which shows a good agreement with the theoretical model. The evolution of the PISHE current with temperature suggests that the PISHE is dominated by the extrinsic mechanism, which is further confirmed by the weak dependence of the PISHE current on the crystal orientation of the sample.
Afkortingen
- 2DEG:
-
Two-dimensional electron gas
- CPGE:
-
Circular photogalvanic effect
- EMF:
-
Circular electromotive force
- FWHM:
-
Volledige breedte op halve maximum
- ISHE:
-
Inverse spin Hall effect
- MBE:
-
Moleculaire bundelepitaxie
- PISHE:
-
Photo-induced inverse spin Hall effect
- ZIJ:
-
Spin Hall effect
- SOC:
-
Spin-baan koppeling
Nanomaterialen
- Werking en toepassingen van de Hall-effectsensor.
- Hall-effect stroomdetectie:open-lus- en gesloten-lusconfiguraties
- Digitale (AAN/UIT) Hall Effect-apparaten:schakelaars en vergrendelingen
- Hall-effect magnetisch ontwerp:frontale en slide-by-configuraties
- Nanogestructureerde elektronenmantel
- Niet-geleiders geleiden stroom op nanoschaal
- Het ontwerp van de emissielaag voor elektronenvermenigvuldigers
- Effect van polyethyleenglycol op de NiO-fotokathode
- Groot lateraal fotovoltaïsch effect in MoS2/GaAs heterojunctie
- Temperatuurafhankelijkheid van Spin-Split Peaks in Transverse Electron Focusing
- Hall-effectsensor begrijpen



