High-Q Fano-resonantie in Terahertz-frequentie gebaseerd op een asymmetrische metamateriaalresonator
Abstract
We stellen een vlak metamateriaal voor dat wordt gevormd door metalen resonatoren met vier stroken, die een hoge Q kunnen bereiken Fano-resonantie in terahertz-regime. Dit terahertz vlakke metamateriaal ondersteunt een scherpe Fano-resonantie bij 0,81 THz met 25% transmissie. De resonantiebandbreedte van de dip is 0,014 THz met de Q -factor 58. De interferentie tussen de lichte modus en de donkere modus leidt tot de Fano-lijnvorm. Dit scherpe Fano-profiel wordt verklaard door de elektromagnetische theorie van Fano-resonantie. Bovendien kunnen meerdere Fano-resonanties worden gerealiseerd door meer strips aan de oorspronkelijke structuur toe te voegen. Als voorbeeld twee Fano-dips met Q -factoren 61 en 65 kunnen worden bereikt via een structuur met vijf stroken.
Achtergrond
Metamateriaal is een soort kunstmatig materiaal met exotische eigenschappen, zoals een negatieve brekingsindex [1] en ultrahoge brekingsindex [2], die in de meeste situaties niet door natuurlijke materialen kunnen worden gerealiseerd. Dergelijk kunstmatig materiaal is samengesteld uit een groot aantal periodieke metalen eenheden en de kenmerken ervan (bijv. permittiviteit en permeabiliteit) kunnen gemakkelijk worden geregeld door de geometrische parameters van de eenheden te veranderen [3]. Als gevolg hiervan heeft de studie van metamaterialen de afgelopen jaren veel aandacht gekregen. Een groot aantal nieuwe toepassingen zijn ontstaan in dit domein, waaronder perfecte absorptie [4, 5], metamateriaalsensoren [6,7,8,9], verhulling [10], Fano-effecten [11], enz.
De lijnvorm van Fano-resonantie is heel anders dan het symmetrische Lorentz-profiel. Het is asymmetrisch en scherp met een relatief hoge Q -factor. Sinds Fano theoretisch het kwantummechanisme van Fano-resonantie [12] onthulde, is het een hot topic geworden. Om de oorsprong van Fano-resonantie te illustreren, zijn er verschillende theorieën opgesteld, waaronder Fano's kwantummechanische analyse [12], klassiek oscillatormodel [13], gekoppelde modustheorie [14] en elektromagnetische theorie van Fano-resonantie [15, 16] . Volgens de elektromagnetische theorie van Fano-resonantie voorgesteld door Gallinet en Martin [16], wordt het kenmerkende Fano-profiel toegeschreven aan de koppeling tussen een niet-stralingsmodus en een stralingsmodus die ook als een continuüm kan worden gezien.
In het terahertz-regime kan de scherpe Fano-resonantie worden bereikt door een zwakke asymmetrie in metamaterialen [17,18,19,20] te introduceren, wat kan leiden tot het verschijnen van een onderliggende donkere modus [21]. Bovendien kunnen grafeenmaterialen ook worden gebruikt om de Fano-resonantie te genereren en zelfs te moduleren [22, 23]. Vergeleken met de meeste EIT (elektromagnetisch geïnduceerde transparantie) [24, 25] en PIT (plasmon-geïnduceerde transparantie) [26, 27], is de Fano-lijnvorm veel scherper en smaller. De Q -factor van Fano [17, 28]-profiel is in veel situaties ongeveer tien keer groter dan die van Lorentz-lijnvorm [29,30,31]. Deze eigenschap maakt Fano-resonantie een veelbelovende keuze om gevoelige detectie te realiseren [8]. Echter, de Q -factor van veel metamaterialen is niet hoog genoeg [17, 32, 33], wat hun toepassingen in termen van detectie beperkt. Om Fano-resonantie breed en efficiënt in detectie toe te passen, is het een noodzakelijke taak om de Q aanzienlijk te verbeteren. -factor van een meta-oppervlak.
Onlangs zijn enkele metamateriaalstructuren ontworpen om hoge Q . te realiseren Fano resonantie. Ding et al. stelde een dubbellaags metamateriaal voor dat bestaat uit twee sets asymmetrische splitringen met verschillende geometrische parameters. Het kan drie Fano-resonanties ondersteunen waarvan Q -factoren zijn respectievelijk 33, 42 en 25 [19]. Een symmetrische dimeerstructuur bestaande uit identieke spit-ringresonatoren op elke laag werd ook gepresenteerd om de Q te verbeteren -factor [34]. Deze gestapelde structuren hebben echter te kampen met technische uitdagingen in de productie. Hoge-Q resonantie met een eenvoudig structuurontwerp blijft nog steeds een hot issue.
In dit artikel demonstreren we een coplanaire metamateriaalstructuur bestaande uit vier metalen strips. In elke eenheidscel zijn drie parallelle stroken loodrecht op de vierde geplaatst. Deze structuur kan een hoge Q . ondersteunen Fano-resonantie (Q -waarde is ongeveer 58) bij 0,81 THz met 25% transmissie. Deze scherpe lijnvorm komt voort uit de interactie tussen de heldere (stralende) modus en de donkere (niet-stralende) modus. Voor verdere discussie wordt de elektromagnetische theorie van Fano-resonantie gebruikt [15, 16]. De eigenschappen van Fano-resonantie kunnen worden gewijzigd door geometrische parameters aan te sturen. De detectieprestaties van het apparaat worden besproken. Door meer strips toe te voegen aan de oorspronkelijk ontworpen structuur, kunnen bovendien meerdere Fano-resonanties worden gerealiseerd.
Methoden/experimenteel
Een groot aantal onderzoeken geeft aan dat het doorbreken van de symmetrie van een structuur een asymmetrische Fano-lijnvorm kan veroorzaken [17, 18, 35,36,37]. Op basis van dit concept ontwerpen we dit metamateriaal met vier stroken dat wordt weergegeven in Fig. 1, waarbij strook 2 is ingesteld om een symmetriebreking te realiseren. Figuur 1a toont het driedimensionale diagram van het voorgestelde metamateriaal. Figuur 1b, c toont respectievelijk het zijaanzicht en bovenaanzicht van de constructie-eenheid. De metalen resonatoren met vier stroken worden bovenop een ideaal diëlektrisch substraat geplaatst waarvan het reële deel van de brekingsindex 1,5 is en het denkbeeldige deel 0. In werkelijkheid komt dit diëlektrische materiaal overeen met silica. Dat wil zeggen, het substraat is verliesloos in het terahertz-gebied. We kiezen voor Au met geleidbaarheid σ = 4.09 × 10 7 S/m om de metalen vlakke resonator te vormen waarvan de dikte 0,2 m is. De herhalingsperiode is P x = P j = 180 m. Drie parallelle stroken (1, 2 en 3) hebben dezelfde grootte. Hun lengte is l x = 120 μm en breedte is w = 20 m. Strook 4 staat loodrecht op de andere stroken (1, 2 en 3). De lengte is l j = 150 μm en breedte is w = 20 m. De afstand tussen de as van strook 2 en het middelpunt van de constructie is d = 30 m. Om dit vlakke metamateriaal te simuleren, wordt de tijdsdomeinmethode met eindig verschil gebruikt. Om simulatietijd en rekengeheugen te besparen, kiezen we de maaswijdten van Δx = Δy = 1 μm en Δz =0,02 m. We vinden dat de simulatieresultaten in dit geval vrij nauwkeurig zijn. Zelfs als kleinere maaswijdten worden toegepast, zijn de simulatieresultaten vrijwel onveranderd. De simulerende randvoorwaarden langs x -as en y -as zijn ingesteld als periodiek, en de voorwaarde langs z -as is ingesteld als perfect op elkaar afgestemde lagen. Figuur la laat zien dat de hele structuur wordt verlicht door een straal van normaal invallende THz-golven. Zoals te zien is in Fig. 1b, c, de elektrische vector E en magnetische vector H van de invallende THz-straal zijn y -as gepolariseerd en x -as gepolariseerd, respectievelijk.
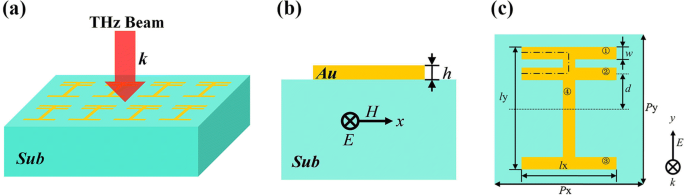
Driedimensionaal diagram van het voorgestelde metamateriaal (a ). Zijaanzicht (b ) en bovenaanzicht (c ) van de asymmetrische metamateriaalresonator; de equivalente lengte l wordt gemarkeerd door een stippellijn
Resultaten en discussie
Het transmissiespectrum van het voorgestelde meta-oppervlak wordt getoond in figuur 2a. Er zijn twee transmissiedips bij de frequenties van 0,430 THz en 0,809 THz met transmissiesnelheden van respectievelijk 0,10% en 26,45%. Om de volgende uitleg beknopter te maken, gebruiken we R s Rs en R d om deze twee resonantiemodi te markeren, R s voor de modus resonant op 0,430 THz en R d voor de resonantiemodus op een hogere frequentie. De optische transmissiesnelheid van R s toont een symmetrisch Lorentz-profiel met een relatief brede bandbreedte van 0,256 THz. Ter vergelijking:R d vertoont een asymmetrische Fano-lijnvorm die veel scherper is met een bandbreedte van 0,014 THz. V -factor is een belangrijk criterium om de lijnvorm te beoordelen. Het kan worden verkregen door de centrale frequentie te delen door bandbreedte. In feite is de Q -factor van R d kan 58, 30 keer meer bereiken dan de Q -waarde van R s , die op veel terreinen bijdraagt aan onderliggende toepassingen. Het bestaan van het asymmetrische Fano-profiel wortelt in de interactie tussen een donkere modus en een heldere modus, d.w.z. de interactie tussen een niet-stralingstoestand en een continuüm, gegenereerd vanuit een stralingstoestand [16, 38, 39]. In de rest van het artikel zal het gedetailleerde mechanisme van de Fano-lijnvorm worden besproken en zullen theoretische transmissiespectra worden geanalyseerd. Hoewel de transmissie bij 0,809 THz 26,45% is in het voorgestelde meta-oppervlak, kan deze verder worden verminderd. Volgens [40, 41] kan het gebruik van diëlektrische materialen met verlies de transmissie verminderen. In onze simulaties is het substraatmateriaal dat we kiezen een ideaal materiaal met een echte brekingsindex van 1,5 dat geen verlies heeft in het terahertz-gebied. Een haalbare methode om transmissie te verminderen, is het gebruik van een lossy materiaal met een complexe brekingsindex om het substraat te vormen in plaats van dit ideale lossless materiaal.
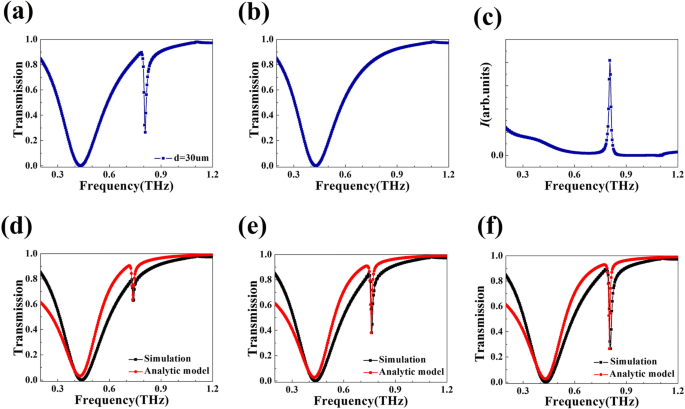
een Transmissiecurve van het ontworpen meta-oppervlak gegeven door numerieke simulatie. b Transmissiespectrum van de heldere modus. c Veldintensiteit van de voorgestelde nanostructuur met vier stroken verlicht door een dipoolbron. d , e , v Gesimuleerd (rode curve) en theoretisch (zwarte curve) transmissiespectrum van de ontworpen structuur met d = 10 μm, d = 20 m, en d = 30 m, respectievelijk
Om de oorsprong van de transmissiecurve te achterhalen, is de verdeling van het elektrische veld ∣E ∣ en de z component van magnetisch veld (H Z ) bij de centrale frequentie van twee resonantiedalingen worden gegeven in Fig. 3. We kunnen grote verschillen vinden tussen de veldverdelingen van R s en R d . Figuur 3a geeft aan dat het elektrische veld van de resonantiemodus R s is voornamelijk geconcentreerd op strook 1 en strook 3, vooral de uiteinden van deze twee stroken. Er is echter zeer weinig elektrische veldverdeling op andere delen van de structuur, inclusief strip 2 en strip 4. Een dergelijke elektrische veldverdeling is te danken aan het elektromagnetische veld van het normaal invallende licht waarvan de elektrische vector E is langs y -as. Daarom, R s kan worden beschouwd als fundamentele resonantie (d.w.z. gelokaliseerde elektromagnetische EM (elektromagnetische) respons) [42]. Trouwens, de verdeling van de z component van magnetisch veld (H Z ) voor modus R s wordt getoond in Fig. 3b waaruit we oppervlaktestroomverdeling kunnen krijgen. Er is aangetoond dat analyse van oppervlaktestroom kan dienen als een essentiële methode om te onthullen hoe de koppeling van modi Fano-resonantie genereert [28]. Zoals getoond in Fig. 3b, vloeit oppervlaktestroom van de bodem naar het bovenste deel van de structuur, wat bijdraagt aan het verzamelen van tegengestelde ladingen aan beide zijden van strip 1 en strip 3. Daarentegen is de veldverdeling bij de centrale frequentie van R d is nogal anders. Intens elektrisch veld wordt gevonden rond strip 1 en strip 2 (Fig. 3c), dat ongeveer vier keer groter is dan dat van de modus R s . Volgens de verdeling van H Z veld getoond in Fig. 3d, is het duidelijk dat de oppervlaktestroom tussen strook 1 en strook 2 omhoog vloeit terwijl de stroom tussen strook 2 en strook 3 tegengesteld vloeit. Op macroniveau kan een dergelijke veldverdeling worden gezien als een soort ladingsinductie tussen de horizontale stroken. Vanuit het perspectief van moduskoppeling is dit fenomeen te wijten aan de interactie tussen de heldere modus en de donkere modus.
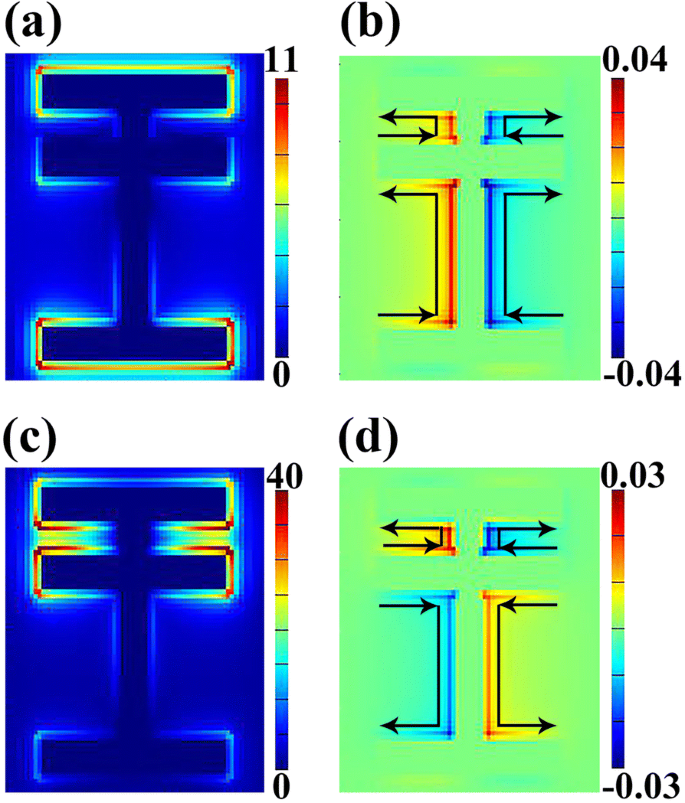
Verdelingen van elektrisch veld ∣E∣ (a ) en z component van magnetisch veld (HZ ) (b ) bij 0,430 THz (R s ); verdelingen van ∣E∣ (c ) en HZ (d ) bij 0,809 THz (R d ); zwarte pijlen in b en d vertegenwoordigen de richting van de oppervlaktestroom
Met het doel onze verklaring te verdiepen en te kwantificeren, worden de spectra van de heldere modus en de donkere modus gesimuleerd en wordt de elektromagnetische theorie van Fano-resonantie [15, 16] gebruikt in de voorgestelde structuur. Figuur 2b toont het transmissiespectrum van een structuur waarvan de periodieke eenheid bestaat uit de stroken 1, 3 en 4. De resonantiemodus ondersteund door een dergelijke structuur kan direct worden geëxciteerd door een vlakke golf; daarom is het de "heldere modus". Daarentegen kan een donkere modus niet worden opgewekt door een straal van vlakke golven; het kan worden geëxciteerd door een snel variërend veld, bijvoorbeeld het nabije veld van een dipool [15, 43]. Figuur 2c toont de veldintensiteit van het vier-strip metamateriaal verlicht door een dipoolbron [44]. De vergelijkingen van Maxwell vormen een solide basis voor de elektromagnetische theorie van Fano-resonantie in nanostructuren. Volgens de vergelijkingen van Maxwell, elektrische vector E voldoet aan de onderstaande golfvergelijking:
$$ {\in}^{-1}\left(\mathbf{r},\upomega \right)\nabla \times \nabla \times \mathbf{E}\left(\mathbf{r},\upomega \ rechts)-\frac{\upomega^2}{{\mathrm{c}}^2}\mathbf{E}\left(\mathbf{r},\upomega \right)=0 $$ (1)waarbij ω de frequentie van de invallende bundel is en ∈(r , ω) is de complexe diëlektrische constante van het verliesgevende materiaal. Het elektrische veld E en de permittiviteit ∈ zijn beide gerelateerd aan de frequentie ω en de positievector r . Twee orthogonale projectie-operators P en Q kunnen worden gebruikt om de golffunctie te scheiden ∣E> in een heldere modus P ∣ E> en een donkere modus Q ∣ E>, d.w.z. een stralingsmodus en een niet-stralingsmodus [15, 38]. Door gecompliceerde afleiding kan de verhouding tussen de sterkte van het totale veld en de intensiteit van de heldere modus worden gegeven als
$$ {I}_{\mathrm{a}}\left(\upomega \right)=\frac{{\left(\frac{\upomega^2-{\upomega_{\mathrm{a}}}^2 }{2{W}_{\mathrm{a}}{\upomega}_{\mathrm{a}}}+q\right)}^2+b}{{\left(\frac{\upomega^2 -{\upomega_{\mathrm{a}}}^2}{2{W}_{\mathrm{a}}{\upomega}_{\mathrm{a}}}\right)}^2+1} $$ (2)waar W een en ωa zijn respectievelijk de bandbreedte en de centrale frequentie van de asymmetrische resonantie. De asymmetrische parameter q en de modulatie demping parameter b zijn beide onmisbaar om I . te beschrijven een (ω) [15, 16]. De vergelijking (2) suggereert dat ik een (ω) vertoont een asymmetrisch profiel, wat uiteindelijk resulteert in de asymmetrische Fano-lijnvorm in de transmissiecurve.
De intensiteit van de heldere modus R s volgt een soepel Lorentziaans profiel. Het hangt af van de frequentie ω en voldoet aan de volgende vergelijking:
$$ {I}_{\mathrm{s}}\left(\upomega \right)=\frac{a^2}{{\left(\frac{\omega^2-{\omega_{\mathrm{s }}}^2}{2{W}_{\mathrm{s}}{\omega}_{\mathrm{s}}}\right)}^2+1} $$ (3)waarvan W s en ω s zijn respectievelijk de bandbreedte en centrale frequentie van het spectrum weergegeven in Fig. 2b, en a is de maximale waarde van de amplitude van de resonantie. De totale kracht I (ω ) van de resonantie kan worden berekend door het product van I een en ik s , waaruit we eindelijk de transmissie T . kunnen krijgen (ω).
$$ I\left(\omega \right)={I}_{\mathrm{a}}\left(\omega \right)\times {I}_{\mathrm{s}}\left(\omega \ rechts) $$ (4) $$ T\left(\omega \right)=1-I\left(\omega \right) $$ (5)Om te voldoen aan de eis van energiebesparing, a mag niet groter zijn dan 1. W een en ω een kan worden berekend uit de centrale frequentie en bandbreedte [15, 16]. De asymmetrische parameter q evenals de modulatie demping parameter b kan worden verkregen via de methode die wordt gegeven door [16]. Op deze manier kunnen we het theoretische transmissiespectrum van deze asymmetrische structuur krijgen. In Fig. 2f vertegenwoordigt de zwarte curve het transmissiespectrum gegeven door de FDTD-methode en de rode curve geeft de resultaten van onze berekening op basis van de elektromagnetische theorie van Fano-resonantie. De consistente trend van zwarte en rode curve geeft aan dat het redelijk is om de transmissiekarakteristieken van de resonator toe te schrijven aan de koppeling van de heldere modus en de donkere modus. Deze conclusie valt ook samen met de veldverdeling in Fig. 3.
De geometrische parameter d beschrijft de afstand tussen de as van strip 2 en het middelpunt van de hele constructie (Fig. 1c). Het kan grote invloed hebben op de centrale frequentie van transmissiedips en hun transmissiecoëfficiënten. Overeenkomstige transmissiespectra met verschillende d worden getoond in Fig. 2d, e. De zwarte curve en de rode curve vertegenwoordigen het transmissiespectrum op basis van respectievelijk simulatie en theoretische berekening. Met d veranderend van 10 naar 30 m, is het duidelijk dat een scherpe Fano-dip dieper wordt, als gevolg van de toenemende koppelingssterkte tussen de lichte modus en de donkere modus. Verder is de centrale frequentie van de modus R d bestaat een duidelijke blauwe verschuiving wanneer strip 2 dichter bij strip 1 wordt geplaatst. Gebaseerd op het LC-circuitmodel, is de resonantiefrequentie van R d wordt gegeven door [45].
$$ {\omega}_{\mathrm{d}}=\frac{1}{2\uppi \sqrt{\mathrm{LC}/2}}\propto \frac{1}{\mathrm{l}} $$ (6)waar l is de equivalente lengte van de corresponderende resonator. Vergelijking (6) geeft aan dat de centrale frequentie ω d is omgekeerd evenredig met l . In onze structuur, equivalente lengte l wordt aangegeven door de lengte van de stippellijn in figuur 1c. Dit komt omdat de veldverdelingen van R d zijn voornamelijk beperkt tot de strook 1 en 2. De lengte van strook 1 (en 2) en de afstand tussen de twee stroken samen bepalen l. Wanneer d toeneemt, neemt de afstand tussen de twee stroken af. Vandaar dat, zoals getoond in Fig. 1c, de equivalente lengte afneemt wanneer d verandert van 10 tot 30 m. Dit leidt tot de toename van R d ’s resonantiefrequentie.
Volgens de theorie van Fano-resonantie, voorgesteld door Fano in 1961 [12], wordt het proces van auto-ionisatie bestudeerd en wordt de asymmetrische lijnvorm van de resonantie toegeschreven aan de interferentie tussen een continuüm en een discrete toestand. Dit is ook de oorsprong van die asymmetrische kenmerken van de metamateriaalresonator die in dit artikel wordt gepresenteerd. Zoals getoond in figuur 4, kan een systeem met drie niveaus worden gebruikt om het overgangsmechanisme van de constructie te verduidelijken. R 0 dient als de grondtoestand van het hele systeem. Heldere modus R 1 is een stralingsmodus die direct kan worden geëxciteerd door de normaal invallende bundel. In dit systeem is de niet-stralingstoestand R 2 kan worden beschouwd als een "donkere modus" [21] zoals eerder besproken. R 2 kan worden opgewonden door het breken van de symmetrie. Het introduceren van een asymmetrie biedt een kanaal om de heldere modus te koppelen aan de donkere modus, en leidt daarom tot de Fano-resonantie [46].
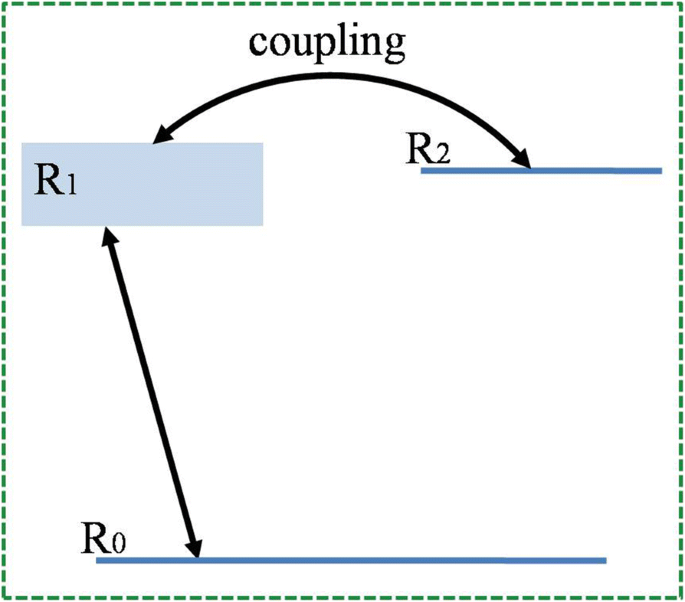
Schematisch diagram van het systeem met drie niveaus
De sterke interactie tussen invallende elektromagnetische golven en de analytlaag zorgt voor een hoge Q Fano-resonantie, een veelbelovende methode om ultragevoelige detectie van brekingsindex n . te realiseren [8]. Het in Fig. 5a voorgestelde apparaat kan functioneren als een effectieve sensor om de brekingsindex n . te detecteren van de analytlaag aan de bovenkant waarvan de dikte 4 m is. De centrale frequentie van de Fano-dip verandert met de verandering van n . Daarom kunnen we de brekingsindex verkrijgen door de resonantiefrequentie van R . te analyseren d . Figuur 5b toont de verschuiving van de resonantiefrequentie van Fano dip in het apparaat. Er verschijnt een duidelijke rode verschuiving wanneer n wordt verhoogd van 1 naar 1,6. De detectiegevoeligheid S is gelijk aan \( \frac{\varDelta f}{\varDelta n} \). Hier, S van de sensor wordt berekend als 0,105 THz/RIU (brekingsindexeenheid). Het is algemeen bekend dat FOM (Figuur van verdienste) een essentieel criterium is voor de prestatie van een sensor [47]. Het kan worden berekend met FOM = \( \frac{S}{\mathrm{linewidth}} \). In deze gepresenteerde structuur kan de FOM-waarde 7.501 bereiken, wat op een ideaal niveau is [47, 48]. Het detectievermogen wordt meestal ook besproken door FOM* = \( \frac{S^{\ast }}{I} \) en S* = \( \frac{\varDelta I}{\varDelta n} \), die is gerelateerd aan de gedetecteerde intensiteit. Het rekenresultaat van S* in deze structuur is 2,6/RIU. En de FOM* in onze structuur is berekend op 10. We hebben ook wat werk verzet om de variatie van de respons met de dikte van de analytlaag te achterhalen. Raadpleeg het aanvullende bestand 1.
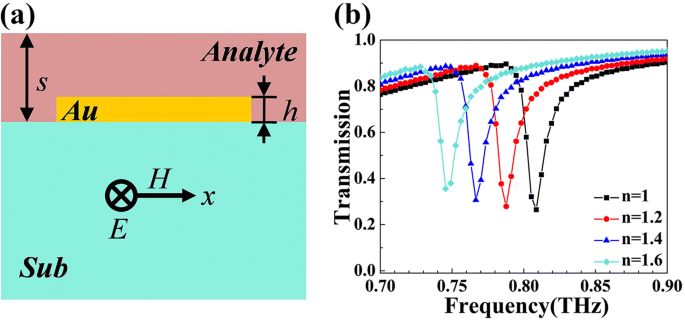
een Dwarsdoorsnede van het sensorapparaat. b Afhankelijkheid van transmissiespectra van de veranderingen van de brekingsindex n
Meerdere Fano-resonanties kunnen in veel situaties worden toegepast. De meeste plasmonische Fano-metamaterialen zijn echter ontworpen om enkele Fano-resonantie te ondersteunen [11, 17]. Daarom is het voor hen niet eenvoudig om meerdere Fano-resonanties te realiseren door de structuur aan te passen. In dit artikel realiseren we meerdere Fano-resonanties door meer horizontale stroken toe te voegen aan het oorspronkelijke ontwerp van het metamateriaal. We presenteren een vijf-strip structuur als een representatief voorbeeld. Het schematische diagram van de vijf-strip resonator wordt getoond in Fig. 6a. De stroken 1, 2, 3 en 4 zijn even groot en evenwijdig aan elkaar. Hun lengte is l x = 120 μm en breedte is w = 20 m. Strip 3 bevindt zich in het midden, en de afstand d tussen de assen van strook 2 en strook 3 is 32 m. Strook 5 staat loodrecht op de andere vier stroken. De lengte is l j = 150 μm en breedte is w = 20 m. De randvoorwaarden en maaswijdte zijn hetzelfde gehouden als bij de simulatie van een vierstrooks resonator. Het simulatieresultaat wordt getoond in Fig. 6b, waarin we duidelijk twee scherpe Fano-dips kunnen vinden bij 0,75 THz en 0,91 THz. De Q waarden van deze twee dips zijn respectievelijk 61 en 65. Er moeten meer Fano-dips worden gegenereerd als er meer horizontale stroken in de structuur worden toegevoegd.
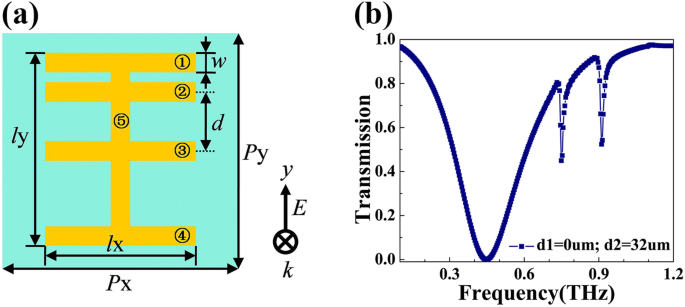
een Bovenaanzicht van de voorgestelde vijfstrokenstructuur. b Gesimuleerde transmissiecurve van de vijf-strip resonator
Conclusie
Concluderend ontwerpen we een vier-strip planaire resonator die scherpe Fano-resonantie kan ondersteunen met een hoge Q -waarde. De bandbreedte van de Fano-dip is 0,014 THz en de Q -factor is 58. De interactie tussen de lichte modus en de donkere modus resulteert in het verschijnen van het asymmetrische Fano-profiel. In dit artikel wordt het theoretische transmissiespectrum berekend. Bovendien, meerdere hoge Q Fano-resonanties kunnen worden gerealiseerd door meer horizontale stroken aan de structuur toe te voegen. Deze structuur kan worden toegepast in detectie- en andere velden.
Afkortingen
- EIT:
-
Elektromagnetisch geïnduceerde transparantie
- EM:
-
Elektromagnetisch
- FOM:
-
Cijfer van verdienste
- PIT:
-
Door plasma veroorzaakte transparantie
- Q :
-
Kwaliteitsfactor
- RIU:
-
Brekingsindexeenheid
Nanomaterialen
- Toepassingen van resonantie
- Nano grafeem, op silicium gebaseerd flexibel transparant geheugen
- Gouden nanobiosensor gebaseerd op de gelokaliseerde oppervlakteplasmonresonantie kan menselijke brucellose diagnosticeren, wat een snelle en betaalbare methode introduceert
- Plasmonische sensor op basis van diëlektrische nanoprisma's
- Het genereren en manipuleren van hoogwaardige factoren van Fano-resonantie in Nanoring-resonator door een halve nanoring te stapelen
- Schatting van supercapacitor-energieopslag op basis van fractionele differentiaalvergelijkingen
- Golflengte-gecontroleerde fotodetector op basis van enkele CdSSe Nanobelt
- Optisch actieve plasmonische metasurfaces gebaseerd op de hybridisatie van in-plane koppeling en out-of-plane koppeling
- Ontwerp van een afstembare ultrabreedband Terahertz-absorber op basis van meerdere lagen grafeenlinten
- Ontwerp van Quad-Band Terahertz Metamateriaal Absorber met behulp van een geperforeerde rechthoekige resonator voor detectietoepassingen
- Ontwerp van bionische cochleaire basilair membraan akoestische sensor voor frequentieselectiviteit op basis van tribo-elektrische film nanogenerator



