Ontwerp van een afstembare ultrabreedband Terahertz-absorber op basis van meerdere lagen grafeenlinten

Abstract

We stellen voor en demonstreren numeriek een ultrabreedband op grafeen gebaseerde metamateriaalabsorbeerder, die bestaat uit meerlaags grafeen / diëlektricum op de SiO₂ laag ondersteund door een metalen ondergrond. Het gesimuleerde resultaat laat zien dat de voorgestelde absorber een bijna perfecte absorptie van meer dan 90% kan bereiken met een bandbreedte van 4,8 Thz. Dankzij de flexibele afstembaarheid van grafeenplaat, kan de toestand van de absorber worden geschakeld van aan (absorptie> 90%) naar uit (reflectie> 90%) in het frequentiebereik van 3-7,8 Thz door de Fermi-energie van grafeen te regelen. Bovendien is de absorber ongevoelig voor de invalshoeken. De breedbandabsorptie kan worden gehandhaafd op meer dan 90% tot 50°. Belangrijk is dat het ontwerp schaalbaar is om bredere afstembare terahertz-absorbers te ontwikkelen door meer grafeenlagen toe te voegen die brede toepassingen kunnen hebben in beeldvorming, sensoren, fotodetectoren en modulatoren.

Achtergrond

In de afgelopen jaren is de terahertz-band een van de meest interessante platforms geworden vanwege de enorme toepassing in spectroscopie, medische beeldvorming, modulatoren, beveiliging en communicatie [1,2,3]. De terahertz-absorber is een belangrijke tak die praktische toepassingen kan vinden in de bovenstaande velden [4,5,6]. De smalle bandbreedte, lage absorptie-efficiëntie en niet-instelbare absorptieprestaties van de absorbers beperken hun toepassingen in de praktijk echter sterk. Om de toepassing van terahertz absorber beter uit te breiden, zijn er dringend meer nieuwe apparaten en materialen nodig. Grafeen, als een tweedimensionaal materiaal met de honingraatstructuur, is een van de meest veelbelovende materialen geworden vanwege de afstembaarheid van geleidbaarheid die wordt gecontroleerd door elektrisch veld, magnetisch veld, poortspanning en chemische doping [7,8,9,10 ,11,12,13,14]. Vooral grafeen kan oppervlakteplasmonen in het terahertz-bereik ondersteunen. Vergeleken met het traditionele oppervlakteplasmonmateriaal hebben grafeenoppervlakplasmonen het voordeel van lage verliezen, flexibele afstembaarheid enzovoort [15,16,17,18,19].

Vanwege de superioriteit van grafeenmaterialen in terahertz-absorptiemiddelen, zijn er enkele grafeenabsorptiemiddelen die zijn voorgesteld en aangetoond [20,21,22,23,24,25,26,27,28,29,30,31,32,33 ,34]. Theoretische analyse bevestigt dat een enkele laag grafeen optisch transparant is en een absorptie van 2,3% heeft [35,36,37]. Om de opsluiting van de elektromagnetische energie te verbeteren, zijn grafeenstructuren met periodieke patronen ontworpen, zoals netvormig [20,21,22], anti-dots [23] en kruisvormig [32]. Deze absorbers zijn echter sterk afhankelijk van complex gestructureerd grafeen, wat resulteert in fabricageproblemen. Bovendien is de beschikbare bandbreedte erg smal en hebben de meeste van de gerapporteerde werken geen bandbreedte van meer dan 1,5 Thz [20,21,22,23,24,25,26,27,28]. Om de bandbreedte te vergroten, zijn verschillende meerlaagse grafeenstructuren voorgesteld. De gerapporteerde meerlaagse structuren zijn echter ook afhankelijk van de zeer complexe structuur van het grafeen en de werkingsbandbreedtes zijn niet lang genoeg [32,33,34]. Bovendien, Zhao et al. ontwierp een schakelbare terahertz-absorber voor de toepassing van amplitudemodulator [25]. Door de chemische potentiaal van grafeen te regelen van 0 tot 0,3 eV, kan de toestand van de ontworpen structuur worden omgeschakeld van absorptie (> 90%) naar reflectie (> 82%) in het frequentiebereik van 0,53-1,05 Thz. Maar de schakelintensiteit is niet hoog genoeg en de modulatiebandbreedte is erg smal, wat de verdere toepassing ervan in de praktijk beperkt.

In dit artikel presenteren we een afstembare, op grafeen gebaseerde terahertz-absorber die is samengesteld uit meerlagig grafeen dat een ultrabreedbandabsorptie van meer dan 90% kan bereiken in het frequentiebereik van 3-7,8 Thz. Het gemiddelde absorptievermogen van de absorber is hoger dan 96,7%. Bovendien heeft de voorgestelde absorber een hogere schakelintensiteit, de absorptieamplitude kan worden afgestemd van bijna perfecte absorptie (> 90%) tot hoge reflectie (> 90%) door de Fermi-energie van de grafeenlaag in de hele bandbreedte van 4,8 Thz te veranderen. Wanneer de Fermi-energie van grafeen 0 eV is, zal de voorgestelde structuur een bijna perfecte reflector zijn met een reflectie van meer dan 97% in de hoge frequentieband (ongeveer 5,5 Thz later). Bovendien is de absorber onafhankelijk van de invalshoeken met een absorptie van meer dan 90% tot 50°. Voor zover wij weten, stellen we eerst de tweedimensionale meerlaagse grafeen/diëlektrische structuur voor om een ultrabreedbandabsorptie te realiseren. De voorgestelde absorber is eenvoudig en is niet afhankelijk van grafeen met complexe patronen, en het ontwerp biedt veel gemak voor de fabricage van meerlaagse grafeenstructuren [38, 39]. Belangrijk is dat het ontwerp schaalbaar is om bredere afstembare terahertz-absorbers te ontwikkelen door meer grafeenlagen toe te voegen, die een brede toepassing kunnen hebben in terahertz opto-elektronische apparaten.

Methoden

Het diagram van de voorgestelde structuur wordt getoond in Fig. 1, die bestaat uit meerlaags grafeen ingebed in het diëlektricum op de SiO₂ laag en een dikke metalen reflecterende plaat aan de onderkant. Zoals weergegeven in Fig. 1, aan de bovenkant, grafeen met verschillende breedte (W ) is ingebed in het diëlektricum op een bepaalde afstand t ₂ (t ₂ =2 m). De breedte W van elk grafeen is respectievelijk 5, 5, 27, 4, 4, 2, 21, 21 en 26 m (van boven naar beneden). Elke laag is symmetrisch rond de z -as. De afstand t ₁ tussen de onderkant van de grafeenlaag en de SiO₂ laag is 2 m. De dikte van het diëlektricum is H ₁ . De middelste laag is SiO₂ met een dikte van H ₂ . De onderkant is een metalen film met een dikte van D . De periode van de eenheid is P. Deze beginwaarden van de structuurparameters zijn ingesteld op H ₁ = 21 μm, H ₂ = 7 μm, D = 0,5 m, P = 32 m. Het onderste metalen materiaal is goud en de permittiviteit ervan kan als volgt goed worden weergegeven door het Drude-model in het terahertz-bereik:

$$ \varepsilon ={\varepsilon}_{\infty }-\frac{\omega_p^2}{\omega^2+ i\omega \gamma} $$ (1)

waarbij de waarde van constante permittiviteit ε _∞ , plasmafrequentie ω _p , en botsingsfrequentie γ zijn ingesteld op 1, 1,38 × 10¹⁶ rad/s, en 1,23 × 10¹³ s^− 1 , respectievelijk. De permittiviteit van het diëlektrische materiaal en SiO₂ materiaal zijn respectievelijk ingesteld op 3 en 4.

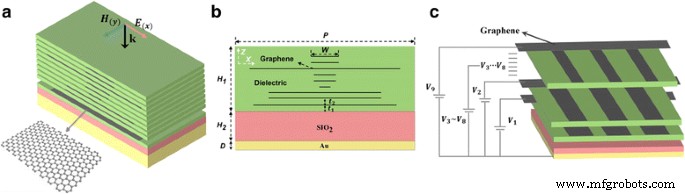
een Schematisch diagram van de op grafeen gebaseerde breedbandabsorber. b Dwarsdoorsnede van de absorber met de parameters die voor de berekening worden gebruikt. c Het schema van het externe biascircuit. De takken van de spanning (V ₁ ~V ₉ ) zijn respectievelijk verbonden met verschillende grafeenlagen

In de simulatie wordt grafeen behandeld als een ultradunne film ingebed in het diëlektricum. De complexe geleidbaarheid van het grafeenoppervlak, gedomineerd door interband- en intrabandbijdragen, kan worden berekend met behulp van de Kubo-formule [40]:

$$ {\displaystyle \begin{array}{l}\sigma \left(w,{E}_f,\tau, T\right)={\sigma}_{\mathrm{inter}}+{\sigma} _{\mathrm{intra}}=\frac{je^2\left(wj{\tau}^{-1}\right)}{\pi {\mathrm{\hslash}}^2}\times \\ {}\left[\frac{1}{{\left(wj{\tau}^{-1}\right)}^2}\underset{0}{\overset{\infty }{\int }}\ frac{\partial {f}_d\left(\varepsilon \right)}{\partial \varepsilon }-\frac{\partial {f}_d\left(-\varepsilon \right)}{\partial \varepsilon } d \varepsilon -\underset{0}{\overset{\infty }{\int }}\frac{f_d\left(-\varepsilon \right)-{f}_d\left(\varepsilon \right)}{{\ left(wj{\tau}^{-1}\right)}^2-4{\left(\varepsilon /\mathrm{\hslash}\right)}^2} d\varepsilon \right]\\ {} \kern0em \end{array}} $$ (2)

waarbij $ {f}_d\left(\varepsilon \right)={\left({e}^{\left(\varepsilon -{E}_f\right)/{k}_BT}+1\right)} ^{-1} $ is de Fermi-Dirac-verdeling, w is de radiale frequentie, ε is de energie, k _B is de constante van Boltzmann, τ is de carrier relaxatietijd, T is de temperatuur (T = 300 K in ons artikel), ℏ is de gereduceerde constante van Plank, en E _f is Fermi-energie. De Kubo-formule (2) geeft aan dat de complexe geleidbaarheid van het grafeenoppervlak kan worden aangepast door Fermi-energie E _f . De grafeen Fermi-energie van elke laag kan afzonderlijk worden geregeld door de voorgespannen spanning, de relatie tussen E _f en vooringenomen spanning kan worden geschreven als [41, 42]:

$$ \left|{E}_f\left({V}_n\right)\right|=\mathrm{\hslash}{v}_F\sqrt{\pi \left|{a}_0\left({V }_n-{V}_0\right)\right|}\kern1.5em \left(n=1,2,3..,9\right) $$ (3)

waar v _F = 0.9 × 10⁶ m/s is de Femi-snelheid, V ₀ is de spanningsoffset [41], $ {a}_0=\frac{\varepsilon_0{\varepsilon}_d}{ed} $, a ₀ is het capacitieve model van de structuur, waarbij ε ₀ is de permittiviteit in vacuüm. ε _d is de permittiviteit van diëlektricum, d is de hoogte van het diëlektricum, en e is de lading van een elektron. V _n (V ₁ ~V ₉ ), dat wil zeggen, de spanning die op het grafeen wordt aangelegd, kan worden verkregen uit het extra circuit van figuur 1c. Volgens formule (2) en (3) kan de geleidbaarheid van het oppervlak van grafeen worden geregeld door de aangelegde spanning. Vervolgens, gebaseerd op de wet van Ampere in stationair regime en de wet van Ohm, kan de permittiviteit van grafeen worden verkregen als [43]:

$$ {\varepsilon}_g=1+i\frac{\sigma_g}{t_g{\varepsilon}_0\omega } $$ (4)

Waarin t _g is de dikte van het grafeen, ε ₀ is de permittiviteit van vacuüm, en σ _g is de oppervlaktegeleidbaarheid van het grafeen. Volgens formule (4) kan de permittiviteit van grafeen worden verkregen door de geleidbaarheid van het oppervlak, die ook kan worden verkregen door de aangelegde spanning. Daarom geeft formule (2-4) aan dat de elektromagnetische eigenschappen van grafeen dynamisch kunnen worden geregeld door de aangelegde spanning, wat ertoe leidt dat de absorptiekenmerken van de structuur ook dynamisch kunnen worden geregeld.

Om de absorptieprestaties van de ontworpen structuur te onderzoeken, implementeren we de numerieke simulaties met behulp van tweedimensionale FDTD. In onze simulatie hebben we de structuur ingesteld op een periodieke randvoorwaarde in de x-richting. Een straal van terahertz vlakke golf valt normaal op het model langs de z richting met zijn elektrisch veld E langs x richting. De Bloch-randvoorwaarde wordt toegepast op de schuine inval in de periodieke structuur. We gebruiken 1-R-T om de absorptie van het model te berekenen, waarbij R en T respectievelijk reflectiviteit en transmissiviteit vertegenwoordigen. Aangezien de dikte van het metaal veel groter is dan de huiddiepte van invallend licht in het metaal, is de doorlaatbaarheid T nul. We vereenvoudigen dus de berekeningsformule voor 1-R.

Resultaten en discussie

Ten eerste stemmen we de spanning van elke grafeenlaag af om een perfecte absorptie te bereiken (van boven naar beneden passen we de Fermi-energie fijn aan E _f van elke grafeenlaag tot 0,9, 0,9, 1,1, 0,8, 0,8, 1,1, 1,1, 0,9 en 0,8 eV). Zoals weergegeven in Fig. 2, van 3 tot 7,8 Thz, heeft de voorgestelde structuur een breedbandabsorptie van meer dan 90% binnen een bandbreedte van 4,8 Thz. De FWHM van de absorber is 5,4 Thz. De bandbreedte is ongeveer $ \frac{BW}{f_0}\times 100\% $ = 88,8% van de centrale frequentie (hier BW is de bandbreedte en f ₀ centrale frequentie is). We berekenen ook het gemiddelde absorptievermogen van de absorber, dat kan oplopen tot 96,7%. Aan de andere kant, met de E _f = 0 eV, de voorgestelde structuur zal een bijna ideale reflector zijn met een reflectie van meer dan 90% over de gehele bandbreedte van de operatie, en in de hoge frequentieband (ongeveer 5,5 THz later), de reflectie zelfs meer dan 97%. Natuurlijk kunnen we ook de spanning van elke grafeenlaag afstemmen om de gewenste amplitude te krijgen die in sommige gebieden potentiële toepassingen kan hebben.

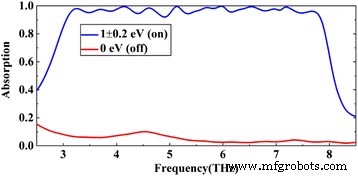
De berekende absorptiespectra van de voorgestelde absorber, waarbij de blauwe lijn de absorptie met hoogspanning weergeeft en de rode lijn de absorptie aangeeft zonder toegepaste spanning

Om de bijna perfecte absorptie in een ultrabrede bandbreedte te verklaren, bespreken we eerst de situatie van een enkele grafeenlaag. Zoals weergegeven in figuur 3a, ontwerpen we de structuur met slechts één enkele grafeenlaag ingebed in het diëlektricum. Op basis van grafeenoppervlakplasmonen onderzoeken we het effect van grafeengerelateerde parameters op de absorptieprestaties van absorbers, inclusief de Fermi-energie E _f , de breedte W , en de positie t van grafeen.

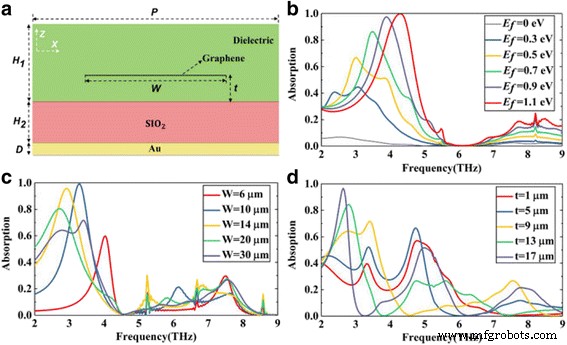
een Schematisch diagram van een enkellaagse grafeenstructuur. b –d De absorptie van de structuurbreedte verschillende Fermi-energie E _f , breedte B , en positie t van het grafeenblad, respectievelijk

Figuur 3b toont de invloed van grafeen Fermi-energie E _f op het absorptiespectrum met vast W en t . Als de toename van E _f , de grafeenoppervlak-plasmonresonantie wordt sterker, de absorptie van de structuur is dienovereenkomstig hoger. De absorptiepiek zelfs meer dan 99% bij 4,3 Thz met de E _f = 1.1 eV. En de resonantie-absorptiepiek beweegt naar een hogere frequentie, blauwverschuiving. Evenzo toont Fig. 3c, d het absorptiespectrum van de structuur met verschillende W of t met ongewijzigde E _f . Door de W . te variëren of t van de grafeenlaag worden respectievelijk de amplitude en frequentie van de resonantiepiek gewijzigd. Dit fenomeen kan worden verklaard door de circuittheorie [28]. In deze theorie wordt grafeen beschreven als een shunt-toegang, waarna het equivalente circuit van de structuur kan worden gemodelleerd met transmissielijnen en grafeen-toegang. Volgens eerder werk [28] kan de grafeentoelating worden gewijzigd met de breedte W en de Fermi-energie E _f van het grafeen. Bovendien is de toelating van de transmissielijnen die overeenkomen met het diëlektricum gerelateerd aan de dikte van het diëlektricum. In onze structuur wordt het diëlektricum gescheiden door een grafeenlaag. Dus de positie t van de grafeenlaag heeft ook invloed op de invoertoegang van de structuur.

Zoals we hierboven hebben besproken, worden door de invloed van grafeengerelateerde parameters op de ingangstoegang van de structuur ook de resonantie-absorptiepieken van het model beïnvloed. Als de invoertoegang van de structuur overeenkomt met de toegang tot de vrije ruimte, wordt de bijna perfecte absorptie bij een bepaalde frequentie bereikt.

Om breedbandabsorptie te bereiken, moeten we vervolgens de resonantie-absorptiepieken toestaan die de toelatingsovereenkomst dicht bij elkaar bereiken. Omdat de absorptiepieken dicht genoeg bij elkaar liggen om samen te smelten, wordt een breedbandabsorptie verkregen. Daarom voegen we grafeenlagen toe om meer resonantie-absorptiepieken te krijgen. En tegelijkertijd passen we de parameters aan die de resonantiepiek beïnvloeden, inclusief E _f , W , en t om toelatingsmatching te implementeren. We voegen eerst twee lagen grafeen toe. Zoals getoond in Fig. 4a, drie lagen grafeen met verschillende breedte W zijn ingebed in het diëlektricum. Er is een bepaald interval t tussen verschillende lagen grafeen of het onderste grafeen van het diëlektricum. We passen de aan grafeen gerelateerde parameters aan de juiste waarden aan, waar we t . instellen = 2 μm, E _f = 0,9 eV, en W =26, 21 en 20 m, respectievelijk (van onder naar boven).

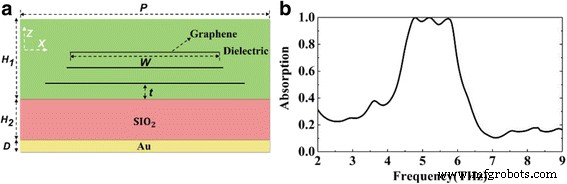
een Schematisch diagram van een drielaagse grafeenstructuur. b De berekende absorptiespectra van een drielaagse grafeenstructuur

Zoals getoond in Fig. 4b, heeft de structuur een bijna perfecte absorptiebandbreedte van 1,3 Thz met een middenfrequentie van 5,25 Thz. Er worden drie resonantiepieken bij 4,7, 5,2 en 5,7 Thz verkregen die overeenkomen met de absorptieamplitude van respectievelijk 99,9, 99,9 en 99,1%. Om een ultrabreedbandabsorptie te bereiken, vergelijkbaar met de drielaagse grafeenstructuur, voegen we meer grafeenlagen toe en passen we de grafeenparameters van elke grafeenlaag aan de juiste waarden aan. We gaan ervan uit dat de structurele parameters vast zijn en de productie is voltooid; we kunnen de Fermi-energie van grafeen dynamisch aanpassen om breedbandabsorptie te bereiken. Op basis van het principe van impedantie-aanpassing en de onderzoekservaring van een drielaagse grafeenstructuur, nemen we eerst aan dat het Fermi-niveau van elke laag grafeen 1 eV is. Zoals getoond in Fig. 5 (a), is de absorptie van de meeste banden meer dan 90%, behalve de band "1" en "2". Afbeelding 5 (a-e) toont het geleidelijke aanpassingsproces voor perfecte absorptie van de "1" en "2" banden. Volgens Fig. 6e, f, wordt de absorptie van de laatste band "1" gedomineerd door de vierde laag (van onder naar boven), dus we passen de Fermi-energie van deze laag individueel aan. Zoals getoond in Fig. 7, wanneer de Fermi-energie 0,8 eV is, is de absorptieprestatie het beste. Dit komt omdat de Fermi-energie de impedantie van grafeen beïnvloedt en vervolgens de ingangsimpedantie van de hele structuur beïnvloedt. De grotere of kleinere Fermi-energie van grafeen zal leiden tot een mismatch in de impedantie. Van a naar b hebben we de absorptieprestaties van de "1"-band verbeterd (in de band voor "1" overlappen de curven a en b elkaar ongeveer). Evenzo vinden we dat de energieverdeling in de "2" -band voornamelijk geconcentreerd is op de 5e, 8e en 9e laag. We hebben eerst de Fermi-energie van de 8e en 9e laag grafeen ingesteld op respectievelijk 0,9 en 0,8 eV. Zoals getoond in Fig. 5, van b tot c, is naast dip "3" en "4", de absorptie van de resterende band in "2" meer dan 90%. Dan, volgens Fig. 6c, wordt dip "3" voornamelijk beïnvloed door de 5e laag grafeen, we stellen de Fermi-energie in op 0,8 eV. Van c naar d is ook het absorptievermogen bij dip “3” verbeterd. Volgens figuur 6d wordt dip "4" echter beïnvloed door alle lagen grafeen. Daarom passen we de Fermi-energie van de resterende grafeenlaag aan naar de juiste waarde. Van d tot e wordt de bijna perfecte breedbandabsorptie bereikt. Vergeleken met de drielaagse grafeenstructuur getoond in Fig. 4, worden meer resonantie-absorptiepieken verkregen, absorptiepieken van verschillende frequenties liggen dicht bij elkaar en gesuperponeerd om een ultrabreedbandabsorptie van meer dan 90% te vormen met een bandbreedte van 4,8 Thz.

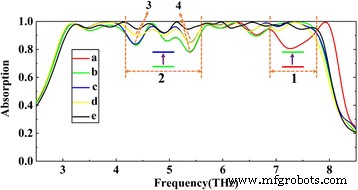
(a)–(e) tonen het geleidelijke aanpassingsproces voor perfecte absorptie. Fermi-energie van elke laag grafeen (van onder naar boven) wordt ingesteld als (a) [1] eV, (b) [1, 1, 1, 0.8, 1, 1, 1, 1, 1] eV, (c ) [1, 1, 1, 0,8, 1, 1, 1, 0,9, 0,8] eV, (d) [1, 1, 1, 0,8, 0,8, 1, 1, 0,9, 0,8] eV, en (e) [0.9, 0.9, 1.1, 0.8, 0.8, 1.1, 1.1, 0.9, 0.8] eV

een –f De verdelingen van de elektrische veldamplitude (|E |) van de voorgestelde absorber bij verschillende frequenties

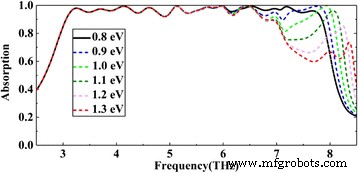
Absorptiespectra met verschillende E _f van de vierde laag grafeen en met ongewijzigde E _f van andere lagen grafeen

Om het fysieke mechanisme achter de ultrabreedband bijna perfecte absorptie te begrijpen, geven we ook een gedetailleerde berekening en analyse van de verdelingen van de elektrische veldamplitude (|E|) van de voorgestelde structuur bij verschillende werkfrequenties. Zoals getoond in Fig. 6, is de energie van het lichtveld beperkt tussen de verschillende lagen grafeen en diëlektricum, wat leidt tot een sterke absorptie. De kenmerken van de elektrische veldverdelingen komen overeen met het absorptiespectrum getoond in Fig. 2. Bij een bepaalde frequentie, bijvoorbeeld, toont Fig. 6b dat de elektrische veldopsluiting voornamelijk te wijten is aan de sterke koppeling van grafeen en diëlektricum als gevolg van de excitatie van gelokaliseerd oppervlakteplasmon (LSP), toont Fig. 6d dat de grafeenoppervlakplasma's een belangrijke rol spelen in de opsluiting van het elektrische veld. De excitatie van gelokaliseerd oppervlakplasmon (LSP) en grafeenoppervlakplasma's dragen samen bij aan de sterke absorptie. Figuur 6a, b, d en figuur 6c, e, f laten zien dat de sterke koppeling tussen grafeen en diëlektricum bij een bepaalde frequentie kan worden veroorzaakt door respectievelijk meerlaags grafeen of monolaags grafeen. Het stapelen van hoge absorptie bij verschillende frequenties zorgt voor een breedbandabsorptie onder invloed van alle lagen grafeen.

Om het stapeleffect beter te illustreren, bijvoorbeeld volgens Fig. 6e, f, wordt de absorptie van de laatste band (ongeveer 6.5 Thz later) voornamelijk gedomineerd door de vierde laag grafeen (van onder naar boven). Dus stemmen we de spanning van deze laag grafeen af. Zoals weergegeven in figuur 7, neemt met de toename van de Fermi-energie van de vierde laag grafeen de absorptie-amplitude van de band na ongeveer 6.5 Thz geleidelijk toe, maar er is bijna geen verandering in de band vóór 6.5 Thz. Op dezelfde manier kunnen we ook onafhankelijk een bepaalde band aanpassen die voornamelijk wordt beïnvloed door andere lagen grafeen. Alle banden die onafhankelijk kunnen worden aangepast voor een hoge absorptie, worden over elkaar heen gelegd om uiteindelijk een breedbandabsorptie te vormen. Net als bij de analyse van figuur 7, illustreert het fenomeen van onafhankelijke aanpassing verder dat het stapeleffect van alle lagen grafeen een bijna perfecte breedbandabsorptie bereikt.

Zoals hierboven besproken, speelt de sterke koppeling tussen grafeen en het diëlektricum een belangrijke rol bij breedbandabsorptie. In de praktische toepassingen hopen we dat de breedbandabsorptie ongevoelig is voor de invalshoeken. Zoals weergegeven in Fig. 8, onderzoeken we het effect van de invalshoeken op de absorber. Uit Fig. 8 kunnen we zien dat de voorgestelde absorber ongevoelig is voor invalshoeken. Hoewel de invalshoek is veranderd in 30°, is het absorptievermogen van de constructie vrijwel onaangetast. Naarmate de invalshoek toeneemt tot 50°, hoewel de absorptie-efficiëntie wordt verminderd, handhaaft de absorber nog steeds een hoge absorptie van meer dan 90% in de gehele werkbandbreedte. Daarom kan de absorber goed werken met een hoge absorptie-efficiëntie over een groot bereik van invalshoeken.

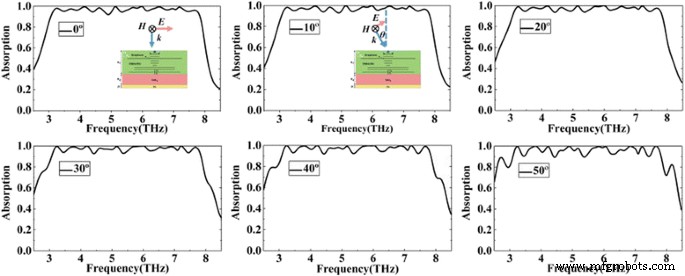
De berekende absorptiespectra van de absorber met verschillende invalshoeken

Ten slotte bespreken we, gezien de moeilijkheden van meerlaagse structuur bij fabricage, het effect van de relevante structuurparameters op de prestaties van de absorber. Figuur 9a, b tonen de absorptiespectra van de voorgestelde absorber met verschillende diktes van de diëlektrische laag H ₁ en met verschillende diktes van de SiO₂ laag H ₂ , respectievelijk. Zoals getoond in Fig. 9a, de meest geschikte hoogte van het diëlektricum H ₁ is 21 urn. Op basis hiervan, H ₁ toename of afname van 0,5 m, de prestaties van de absorber hebben bijna geen verandering. Zelfs als H ₁ verandert met 1 μm, handhaaft de absorber nog steeds een absorptie van meer dan 90% in de meeste banden behalve de band rond 7 THz. Zoals getoond in Fig. 9b, vergeleken met H ₁ , de absorber is gevoeliger voor de hoogte van de SiO₂ H ₂ . Zelfs in dit geval behoudt de absorber, naast de band rond 6 en 7,1 Thz, ook een goede prestatie in de meeste banden. Zoals hierboven besproken, kunnen we vinden dat hoewel de dikte van de diëlektrische laag en de SiO₂ laag zijn zelfs op micronschaal veranderd, behoudt de absorber nog steeds een goede absorptieprestatie in de meeste golflengten, wat de robuustheid van de absorber in de fabricage aanzienlijk zal verbeteren.

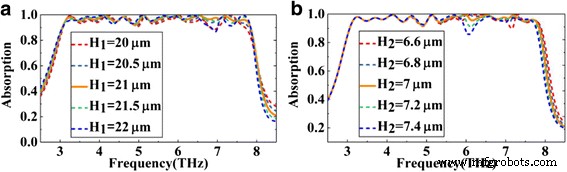
De gesimuleerde absorptiespectra van de voorgestelde absorber met verschillende diktes van de diëlektrische laag en met verschillende diktes van de SiO₂ laag die overeenkomt met a en b

Conclusies

In dit artikel stellen we een ultrabreedband, afstembare, op grafeen gebaseerde terahertz-absorbeerder voor, bestaande uit meerdere lagen grafeen/diëlektricum. De voorgestelde absorber kan een breedbandabsorptie van meer dan 90% bereiken met een bandbreedte van 4,8 Thz door de Fermi-energie E te veranderen _f van verschillende grafeenlagen. Met de E _f = 0 eV, zal het voorgestelde ontwerp een bijna ideale reflector zijn met een reflectie van meer dan 90% binnen de totale bedrijfsbandbreedte van 3-7,8 THz. De ultrabreedbandabsorptie wordt toegeschreven aan het stapeleffect van sterke resonantieabsorptie bij verschillende frequenties die worden geëxciteerd door gelokaliseerd oppervlakplasmon (LSP) en grafeenoppervlakplasmonen. Bovendien is de voorgestelde absorber ongevoelig voor de invalshoeken en vinden we ook dat de dikte van de diëlektrische laag en de SiO₂ laag heeft weinig effect op de absorptieprestaties, wat gunstiger is voor praktische toepassingen. Bovendien is de voorgestelde absorber eenvoudig die niet afhankelijk is van complex gestructureerd grafeen en kan de bandbreedte worden vergroot door meer grafeenlagen toe te voegen. Deze afstembare breedbandabsorber kan grote potentiële toepassingen hebben in fotodetectoren, beeldvorming en modulatoren.

Afkortingen

FDTD:: Tijdsdomein met eindig verschil
LSP:: Gelokaliseerd oppervlakteplasmon

Optisch actieve plasmonische metasurfaces gebaseerd op de hybridisatie van in-plane koppeling en out-of-plane koppeling Tweedimensionale VO2 mesoporeuze microarrays voor krachtige supercondensator

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal