Kleine hoekverstrooiing van vetfractalen op nanoschaal

Abstract

Verstrooiing onder een kleine hoek (van neutronen, röntgenstraling of licht; SAS) wordt beschouwd als de structurele kenmerken van deterministische vetfractalen op nanoschaal. We laten zien dat in het geval van een polydispers fractaal systeem, met gelijke waarschijnlijkheid voor elke oriëntatie, men de fractale dimensies en schaalfactoren op elk structureel niveau verkrijgt. Dit is in overeenstemming met algemene resultaten afgeleid in de context van kleine-hoekverstrooiingsanalyse van een systeem van willekeurig georiënteerde, niet-interagerende nano-/microfractalen. We passen onze resultaten toe op een tweedimensionale dikke Cantor-achtige fractal, waarbij we analytische uitdrukkingen berekenen voor de verstrooiingsintensiteiten en structuurfactoren. We leggen uit hoe de structurele eigenschappen kunnen worden berekend uit experimentele gegevens en laten hun correlatie zien met de variatie van de schaalfactor met het iteratiegetal. Het model kan worden gebruikt om geregistreerde experimentele SAS-gegevens te interpreteren in het kader van vetfractalen en kan structurele eigenschappen van materialen onthullen die worden gekenmerkt door een reguliere wet van verandering van de fractale afmetingen. Het kan opeenvolgingen van verval van de machtswet beschrijven, met willekeurige afnemende waarden van de verstrooiende exponenten, en afgewisseld met regio's met een constante intensiteit.

Inleiding

Veel hiërarchische structuren die op nano- en microschaal zijn gegenereerd, hebben geometrische kenmerken die onveranderlijk zijn onder schaaldilataties, die zelfgelijkenis vertonen en dus fractale eigenschappen dragen [1, 2]. Hoewel recente vorderingen in materiaalwetenschap en nanotechnologie de voorbereiding van verschillende kunstmatige deterministische fractals op nano-/microschaal mogelijk maken, met een exacte zelfgelijkenis [3-7], genereert de overgrote meerderheid van natuurlijke processen willekeurige, statistisch zelfgelijkende fractals. Een goede benadering in de structurele studies van natuurlijke fractale formaties kan worden gedaan door gebruik te maken van deterministische fractale modellen, met dezelfde fractale dimensie als de willekeurige. Deze benadering werd met succes gebruikt om aan te tonen dat de overdracht over willekeurige fractale oppervlakken zeer dicht bij de respons van deterministische modelgeometrieën ligt [8]. Door polydispersiteit te introduceren in het constructiealgoritme van een deterministische fractal, kunnen vergelijkbare small-angle scattering (SAS) intensiteiten worden verkregen als die overeenkomen met willekeurige fractals [9]. Bovendien is een "deterministische" benadering rekenkundig efficiënter, waardoor een analytische beschrijving van verschillende eigenschappen mogelijk is, zoals fractale vorm, structuurfactoren en de gyratiestraal.

Een van de meest betrouwbare methoden om de structurele eigenschappen van zowel deterministische als willekeurige fractals [10, 11] te bepalen, is het gebruik van golfdiffractie in de context van kleine-hoekverstrooiing op nano- of microgestructureerde materialen, met behulp van neutronen of elektromagnetische golven (x -straal, licht, enz.) [12]. Daarom is een van de fundamentele taken in theoretische beschrijvingen die verband houden met experimentele bepalingen in dit onderzoeksgebied, het onthullen van de relatie tussen de structuur van fractals en hun overeenkomstige diffractiespectrum of verstrooiingsintensiteitsverdeling versus verstrooiingsgolfvector. In deze richting zijn veel experimentele en theoretische studies uitgevoerd [13–21].

Met behulp van standaard theoretische berekeningen en interpolatie is de parameter die wordt bepaald uit dit soort experimentele metingen de massafractale dimensie D _m (zie Bijlage 1), met D _m D _s , met d −1<D _s <d . We hebben aangegeven met d de Euclidische dimensie waarin de fractal is ingebed. De massafractale dimensie beschrijft de manier waarop de massa M (r ) varieert wanneer het is ingebed in een schijf met straal r . De verkregen massastraal relatie $M(r) \propto r^{D_{\mathrm {m}}}$ leidt tot het gedrag van de verstrooiingsintensiteit $I(q) \propto q^{-D_{\mathrm {m} }}$. Blijkbaar, D _m kan worden geïdentificeerd met de exponent van de machtswet-afhankelijkheid van de verstrooiingsintensiteit als functie van de verstrooiingsgolfvector q [18, 22]. Hoe hoger de waarde van D _m , hoe compacter de structuur is. Evenzo, in het geval van een oppervlaktefractal, gehoorzaamt zijn oppervlakteverdeling $S(r) \propto r^{2-D_{\mathrm {s}}}$, en dus $\phantom {\dot { i}\!}I(q) \propto q^{-(2\mathrm {d}-D_{\mathrm {s}})}$ [19, 23]. Werkend in de driedimensionale Euclidische ruimte, D _s benadert het minimum van twee, wanneer het oppervlak bijna perfect glad is. Het neigt naar het maximum van drie, als het zo opgevouwen is dat het de ruimte bijna volledig vult.

Veel experimentele diffractie-intensiteiten van verschillende chemisch gesynthetiseerde en biologische systemen worden op een dubbele logaritmische schaal gekenmerkt door een opeenvolging van verval van de machtswet, afgewisseld door gebieden met een constante intensiteit. Dit gedrag kan worden geïdentificeerd voor sommige polymeergels [24], glycosidehydrolase voor cellobiosesubstraat [25], polyelektrolytcomplex-coacervaten [26] of nanoporeuze koolstof [27]. Hoewel het klassieke Beaucage-model [28] elementaire structurele informatie over deze systemen kan verschaffen (dwz massa- of oppervlaktefractale dimensie en de totale grootte van elk structureel niveau), is een meer volledige karakterisering nodig vanwege het grote aantal configuraties dat overeenkomt met een vaste waarde van de fractale dimensie. Dit probleem is onlangs gedeeltelijk aangepakt door Cherny et al. [29] in de context van de small-angle scattering (SAS)-modellen. Er werd aangetoond dat voor deterministische massafractalen met een enkele schaal aanvullende informatie kan worden verkregen, zoals het fractal iteratiegetal, het aantal basiseenheden en de schaalfactor. Deze benadering werd bovendien met succes gebruikt om nieuwe modellen voor vette fractals te ontwikkelen, als opeenvolgingen van machtswetverval aanwezig zijn in de verstrooiingsverdelingen. Het kan worden toegepast op constructies waarvan de totale grootte van de basiscomponenten in dezelfde orde van grootte is als de onderlinge afstanden [30, 31].

Het theoretische model dat in dit artikel wordt gepresenteerd, combineert eerdere modellen om hun toepasbaarheid uit te breiden. Het beschrijft opeenvolgingen van verval van de machtswet, met willekeurig afnemende waarden van de verstrooiende exponenten, en afgewisseld met regio's van constante intensiteit. Ons model is ook in staat om meer gedetailleerde informatie te geven over elk structureel niveau in de nano-/microfractal. Voor dit doel beschouwen we een dikke fractal, weergegeven door een tweedimensionale deterministische massafractal met een schaalfactor die iteratiegetalafhankelijk is, maar met een niet-verdwijnend oppervlak in de limiet van een groot aantal iteraties, dus met een positieve Lebesgue maatregel. We leiden analytische uitdrukkingen af van de fractale vorm- en structuurfactoren, en we laten zien hoe de fractale dimensies en schaalfactoren op elk structureel niveau kunnen worden bepaald.

Theoretische achtergrond

Gezien een reeks op dezelfde manier georiënteerde, identieke diffractieopeningen, hier aangeduid met Σ , met N transparante regio's, gelabeld met j , moet rekening worden gehouden met een sommatie over de amplitudes die zijn verkregen uit elke opening. Dus de bekende frequentieverdeling van de diffractie-amplitude van een enkele opening (Vgl. (37) in Bijlage 2) kan worden herschreven als [32]:

$$ A(p,s) =\sum\limits_{j=1}^{N} \iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{- 2 i \pi \left(p(x+x_{j}) + s(y+y_{j})\right)}\mathrm{d}x\,\mathrm{d}y. $$ (1)

De coördinaten van een punt in het lokale frame van de j het diafragma is (x _j ,j _j ), en T (x,y ) vertegenwoordigt de individuele transmissiefunctie die overeenkomt met elk transparant gebied. Men kan sommatie uitwisselen met integratie omdat in ons geval de openingen worden beschreven door dezelfde individuele verdelingsfunctie, zodat Vgl. (1) kan worden herschreven als:

$$ A(p,s) =\iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{-2 i \pi (px + sy)}\mathrm{ d}x\,\mathrm{d}y \times \sum\limits_{j=1}^{N}e^{ipx_{j}}e^{isy_{j}}. $$ (2)

De integraalfactor van de vorige gelijkheid vertegenwoordigt de Fourier-transformatie van de verdelingsfunctie van elk van de identieke openingen, zoals hierboven vermeld. Deze amplitude wordt gemoduleerd door de factor die de sommatie bevat, die de Fourier-transformatie vertegenwoordigt van Dirac-delta-verdelingen van de vorm $A_{\delta }~=~\sum _{j~=~1}^{N}(x~ -~x_{j})(y~-~y_{j})$. Daarom wordt ook rekening gehouden met de ruimtelijke verdeling van de openingen in de array. Dus, vgl. (2) kan worden herschreven in de vorm die bekend staat als de matrixstelling [32]:

$$ A(p,s)~=~\mathcal{F}\left\{T(x,y)\right\} \mathcal{F}\left\{A_{\delta}\right\}. $$ (3)

De intensiteitsverdeling van het afgebogen beeld in het Fourier-vlak wordt:

$$ I(p,s) \equiv \left| A(p,s) \right|^{2} =\left|\mathcal{F}\left\{T(x,y)\right\}\right|^{2} \big|\mathcal{F }\left\{A_{\delta}\right\}\big|^{2}. $$ (4)

Zoals te verwachten is, komt de eerste factor in het product overeen met de verstrooiingsintensiteit van een enkel gat, terwijl de tweede de manier onthult waarop deze gaten zijn verdeeld binnen de diffractie-opening Σ . Deze hoeveelheden staan ook bekend als de vormfactor F (p,q ) en respectievelijk de structuurfactor S (p,q ). Dit is de reden waarom de resultaten die in het hele document zijn verkregen, worden uitgedrukt met behulp van de volgende vorm van verstrooiingsintensiteit:

$$ I(p,q) \equiv F(p,s) S(p,s). $$ (5)

Vet fractaal model en methode

De gedetailleerde procedure voor het construeren van een dunne (gewone) Cantor-fractal is bekend [33]. Alleen de belangrijkste bouwprocedure wordt hier samengevat. Er wordt gekozen voor een benadering van boven naar beneden. Beginnend met een initieel vierkant (of een andere Euclidische vorm) van rand l ₀ (om m =0), waarvan het middelpunt samenvalt met de oorsprong van het cartesiaanse coördinatensysteem en de randen evenwijdig aan de assen van het coördinatensysteem, elk punt in het vierkant voldoet aan de voorwaarden −l ₀ /2≤x ≤l ₀ /2 en −l ₀ /2≤y ≤l ₀ /2. Bij de eerste iteratie (m =1), is het vierkant verdeeld in vier andere vierkanten, met randlengte $\beta _{\mathrm {s}}^{(1)}l_{0}$. We hebben aangegeven met $\beta _{\mathrm {s}}^{(1)} \equiv (1-\gamma _{1})/2$, met $0 <\beta _{\mathrm { s}}^{(1)} <1/2$, de eerste iteratie-schaalfactor, en met γ ₁ de fractie van de verwijderde lengte op dit punt, zoals te zien is in Fig. 1 a, b) voor m =1. Het getal tussen (⋯), dat als bovenste index verschijnt, kwantificeert het iteratienummer. Het moet niet worden geïnterpreteerd als een exponent van een machtsfunctie. In termen van de schaalfactor worden de posities van de vier vierkanten gegeven door de vectoren $\boldsymbol {a}_{j}~=~\left \{ \pm \beta _{\mathrm {t}}^{ (1)}l_{0}, \pm \beta _{\mathrm {t}}^{(1)}l_{0}\right \}$ met alle mogelijke tekencombinaties, waarbij $\beta _{ \mathrm {t}}^{(1)}~=~\left (1-\beta _{\mathrm {s}}^{(1)}\right)/2$ wordt gebruikt om formuleringen verder te vereenvoudigen. Vanwege de eenvoud van numerieke berekeningen werd als initiële vorm gekozen voor het vierkant. Elke andere geometrische vorm, bijvoorbeeld een cirkel, kan worden overwogen. Het effect van het kiezen van een andere vorm wordt alleen waargenomen in het Porod-gebied van de vormfactor, wat buiten het bestek van dit artikel valt.

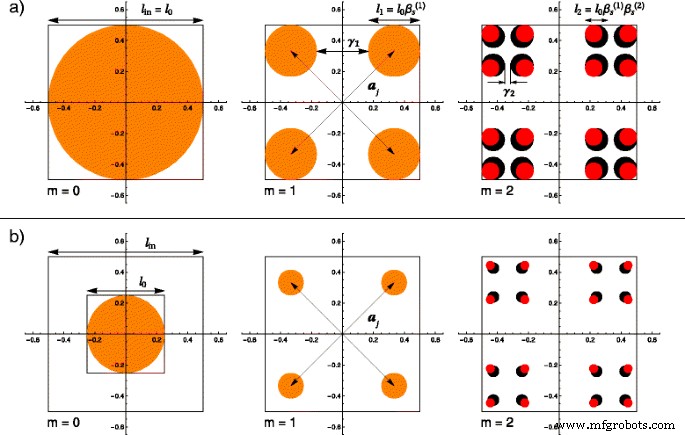
(Online kleur) Een vergelijking tussen gewone en dikke fractals voor de eerste twee iteraties, waarbij de basisvorm op m =0 is een schijf met een diameter l ₀ en de fractale grootte is l _in :een ik ₀ =l _in; b ik ₀ =l _in /f , met f =2. In beide gevallen, op m =1 de structuren vallen samen door gelijke schaalfactoren $\beta _{\mathrm {s}}^{(1)}$. Beginnend met m =2, de dikke fractal heeft een grotere schaalfactor $\left (\beta _{\mathrm {s}}^{(2)}> \beta _{\mathrm {s}}^{(1)}\ rechts)$, en dus hebben schijven een grotere diameter (zwarte schijven ) dan in het geval van gewone fractal (rode schijven ); een _j zijn de positievectoren en γ _ik zijn de fracties van de verwijderde lengte bij i de iteratie

De eerste twee hierboven beschreven stappen worden ook toegepast bij de constructie van de klassieke versie van een dikke fractal, voor iteraties m =0 en m =1. Dit is de reden waarom, tot nu toe, deze twee structuren samenvallen. Om de vetfractal te verkrijgen, is een wijziging van het algoritme gebruikt bij iteratie m =1 moet worden gedaan door een andere schaalfactor te kiezen op m =2, $\beta _{\mathrm {s}}^{(2)} \equiv (1 - \gamma _{2})/2$. Door het hele algoritme toe te passen binnen de limiet van een groot aantal iteraties [34, 35], verkrijgt men opnieuw de klassieke versie van een dikke fractal. Uit de constructie blijkt duidelijk dat de reguliere versie van de fractal wordt hersteld wanneer de schaalfactoren bij elke iteratie gelijk worden gekozen $\beta _{\mathrm {s}}^{(1)}~=~ \beta _{\mathrm {s}}^{(2)}~=~\cdots =\beta _{\mathrm {s}}^{(m)}$.

Om het constante plateau tussen twee machtswet-verval in het gedrag van SAS-intensiteit te verkrijgen, moeten we er rekening mee houden dat de afstanden tussen de verstrooiingseenheden veel groter zijn dan hun totale grootte. Een dergelijke benadering werd eerst gebruikt in de context van oppervlaktefractale modellen [36, 37]. Gezien de verhouding f van de totale afstand tussen de verstrooiingseenheden l _in en hun totale grootte l ₀ , men heeft:

$$ f~\equiv~ l_{\text{in}}/l_{0}. $$ (6)

Voor verstrooiingsexperimenten die plateaus van constante intensiteit tussen twee fractale gebieden weergeven, worden waarden van f ≫1 moet worden gekozen. In het geval van oppervlaktefractalen, het verhogen van de waarde van f leidt tot een betere overeenkomst tussen de totale SAS-intensiteit enerzijds en de benadering van onafhankelijke verstrooiingseenheden anderzijds [36, 37].

Met behulp van bovenstaande overwegingen kan men de verschillen tussen gewone en dikke fractals beschrijven. De invloed van de factor f , hierboven geïntroduceerd, kan ook worden gevisualiseerd. Dit is de reden waarom we in Fig. 1 de vergelijking grafisch illustreren met behulp van een schijf met straal r ₀ ≡l ₀ /2=l _in /(2f ) als onze basisvorm. De resultaten van de eerste twee iteraties, weergegeven in elke rij van Fig. 1, vertegenwoordigen de structuren die zijn verkregen voor een reguliere fractal (gemarkeerd door rode schijven) en een dikke fractal (weergegeven als een zwarte schijf), die ook volledig over elkaar kan worden gelegd ( gemarkeerd als oranje schijven). In de rij met het label Fig. 1a, de factor f wordt beschouwd als gelijk aan de eenheid zodat de klassieke constructies en fractale vormen worden verkregen. De tweede rij van de figuur, aangeduid in Fig. 1b, vertoont de invloed van de hierboven gepresenteerde factor. In deze berekeningen kozen we de willekeurige waarde van f =2. Men merkt op dat bij iteraties m =0 en m =1, in zowel a- als b-gevallen zijn de verkregen structuren van de reguliere en dikke Cantor-sets identiek en volledig overlappend. Dit is te verwachten vanwege de gemeenschappelijke schaalfactor. Zoals echter te zien is in het laatste paar afbeeldingen van Fig. 1, beginnend met m =2, zijn de stralen van de schijven van de dikke fractal groter omdat de schaalfactor $\beta _{\mathrm {s}}^{(2)}$ per definitie groter is dan die van de gewone. In de laatste afbeelding van Fig. 2b is de grootte van de schijven veel kleiner dan in zijn tegenhanger van Fig. 2a vanwege de niet-eenheidswaarde van de factor f .

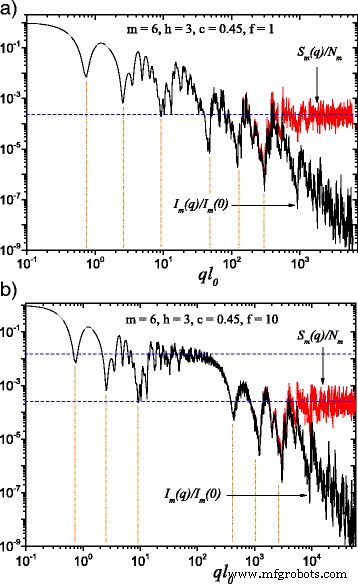
(Kleur online) Een vergelijking tussen de verstrooiingsintensiteit gegeven door Vgl. (22) (zwarte rondingen ) en structuurfactor gegeven door Vgl. (24) (rode curven ) om m =6 en gemiddeld over oriëntaties volgens Vgl. (25). Hier, h =3 (d.w.z. de schaalfactor wordt gedurende drie opeenvolgende iteraties constant gehouden), terwijl de basisvorm bij het berekenen van de verstrooiingsintensiteit een vierkant is met de randgrootte l ₀ :een ik ₀ =l _in; b ik ₀ =l _in /f (met f =10). Wanneer f ≠1, een plateau van constante intensiteit verschijnt tussen de twee gegeneraliseerde machtswetverval (Fig. 2b). Horizontale lijnen noem de asymptoot van de structuurfactor ≃1/N _m , terwijl de minima-posities worden geschat volgens Vgl. (26)

Om de machtswetten zelf te verkrijgen, moet men het klassieke vetfractalmodel verder veralgemenen. Dit wordt gedaan door te bedenken dat de schaalfactorveranderingen niet bij elke iteratie worden gedaan, maar bij elke seconde, derde, ⋯, of, in het algemeen, elke h de iteratie. De fractie van verwijderde lengtes bij de m de iteratie is:

$$ \gamma_{m}~=~c^{p_{m}}, $$ (7)

met 0<c <1. De functie p _m is gedefinieerd als:

$$ p_{m} \equiv \left\lfloor 1+\frac{m-1}{h} \right\rfloor, $$ (8)

voor elke positieve gehele waarde van m , met h =1,⋯,m , waarbij de verdiepingsfunctie ⌊⋯ ⌋ werd gebruikt. Dus de schaalfactor die overeenkomt met de m de iteratie wordt gegeven door:

$$ \beta_{\mathrm{s}}^{(m)}~=~\frac{1-\gamma_{m}}{2}. $$ (9)

Het is nu duidelijk dat het doel van de functie p _m is om de schaalfactor constant te houden voor h iteraties (h <m ).

De componenten van positievectoren van elk vierkant kunnen worden geschreven als:

$$ \beta_{\mathrm{t}}^{(m)} =\frac{\beta_{\mathrm{s}}^{(m)}}{2} + \frac{\gamma_{m}} {2}, $$ (10)

terwijl de lengte van de rand van elk vierkant wordt gegeven door:

$$ l_{m}=\frac{l_{0}}{2^{m}}\prod_{i=1}^{m}(1-\gamma_{i}). $$ (11)

De factor f moet worden gebruikt in de formule van de lengte l ₀ om er rekening mee te houden dat voor iteraties tussen de (h +1)de en m e, de grootte van vierkanten neemt af met betrekking tot de afstanden ertussen:

$$ l_{0} =\left\{\begin{array}{ll} l_{\text{in}}, &\mathrm{for~~iteraties~~} \leq h \\ l_{\text{in }}/f, &\mathrm{voor~~iteraties~~}> h, \end{array}\right. $$ (12)

waar h <m . Het aantal vierkanten bij elke iteratie is:

$$ N_{m}~=~4^{m}. $$ (13)

Dus op elke schaal, beschouwd als iteratie met constante schaalfactor, heeft men een andere fractale dimensie gegeven door [29, 38, 39]:

$$ D_{\mathrm{m}}~=~-\frac{2 \ln 2}{\ln \beta_{\mathrm{s}}^{(m)}}. $$ (14)

Binnen de limiet van een groot aantal iteraties zal de fractale dimensie van de geconstrueerde fractal set [34] zijn:

$$ D \equiv \lim\limits_{m \rightarrow \infty}{\frac{\ln N_{m}}{\ln (l_{0}/l_{m})}} =2, $$ (15 )

wat de verwachte waarde is voor een tweedimensionale vetfractal. Tot slot, als een _ik is het relatieve gebied verwijderd bij i de iteratie, dan $\prod _{i=1}^{m}(1-a_{i})> 0$ if $\sum _{i=1}^{\infty } a_{i} <\infty $, en daarmee voldoet het model aan de definitie en kenmerken van dikke fractals [35].

Resultaten en discussie

Volgens het Babinet-principe kunnen we concluderen dat op m Bij deze iteratie zijn de openingen in het rooster de resterende vierkanten in de fractal, terwijl de verwijderde delen ondoorzichtig worden voor de straling.

Intensiteit van monodisperse verstrooiing en structuurfactor

Om de analytische uitdrukking van de verstrooiingsintensiteit voor de dikke Cantor-fractal af te leiden, beginnen we met het schrijven van de recursierelatie van de roostertransmissie voor een willekeurige iteratie die overeenkomt met 1D geval. Om m =0, we hebben

$$ T_{0}(l_{0}, x) \equiv \text{rect}(l_{0}, x) =\left\{\begin{array}{ll} 1, &|x| Rekening houdend met het constructie-algoritme van de fractal, wordt de transmissie na de eerste iteratie gegeven door:

$$ \begin{aligned} T_{1}(l_{1}, x,) =T_{0}(l_{1}, x) \ast \delta\left(\frac{x-l_{0}\ beta_{\mathrm{t}}^{(1)}}{l_{1}}\right) + \\ T_{0}(l_{1}, x) \ast \delta\left(\frac{x +l_{0}\beta_{\mathrm{t}}^{(1)}}{l_{1}}\right),~~~~~~~~~~~~ \end{aligned} $$ (17)

waar δ (x −een ) is de eendimensionale Dirac-delta-verdeling bij x =een . Het symbool ∗ vertegenwoordigt de convolutie-operator. Daarom, om m de iteratie kunnen we schrijven:

$$ \begin{uitgelijnd} T_{m}(l_{m}, x) =T_{m-1}(l_{m}, x) \ast \delta\left(\frac{x-u_{m} }{l_{m}} \right) + \\ T_{m-1}(l_{m}, x, y) \ast \delta\left(\frac{x+u_{m}}{l_{m }} \right),~~~~~~~~~~~~ \end{aligned} $$ (18)

waarbij $u_{m}~=~l_{0}\beta _{\mathrm {t}}^{(m)}\prod _{j=1}^{m-1}\beta _{\mathrm {s}}^{(j)}$. Het uitvoeren van een Fourier-transformatie op Vgl. (18), vindt men dat de verstrooide amplitude bij m de iteratie is:

$$ A_{m}(p)=2^{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\prod\limits_{i=1}^{ m}\cos(2\pi p u_{i}). $$ (19)

Sinds de 2D vetfractal-model is een direct product van twee eendimensionale vetfractalen, de Fourier-transformatie kan worden geschreven als een product van twee eendimensionale Fourier-transformaties. Daarom kan de tweedimensionale verstrooiingsamplitude worden geschreven als:

$$ A_{m}(p,s)\equiv A_{m}(p) A_{m}(s), $$ (20)

en dus,

$$ \begin{uitgelijnd} A_{m}(p, s) =N_{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin (\pi s l_{m})}{\pi s l_{m}} \times \\ \prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}), \end{uitgelijnd} $$ (21)

zodat de verstrooiingsintensiteit wordt:

$$ \begin{uitgelijnd} I_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin( \pi s l_{m})}{\pi s l_{m}} \right)^{2} \times \\ N_{m}^{2} \left(\prod\limits_{i=1}^ {m}\cos(2\pi p u_{i})\cos(2\pi s u_{i}) \right)^{2}. \end{uitgelijnd} $$ (22)

De eerste factor in de vorige vergelijking, die de diffractie-intensiteit weergeeft als gevolg van de vormfactor, zoals vermeld in Vgl. (5):

$$ F_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin(\pi s l_{ m})}{\pi s l_{m}} \right)^{2}, $$ (23)

komt overeen met de verstrooiingsintensiteit verkregen uit een enkel vierkant van de rand l _m . De tweede factor, die de diffractie-intensiteit weergeeft vanwege de structuurfactor, zoals vermeld in Vgl. (5):

$$ S_{m}(p, s) =N_{m}^{2}\left(\prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}) \right)^{2}, $$ (24)

beschrijft de manier waarop vierkanten worden verdeeld. De totale intensiteit van de verstrooide straling is het product van F _m (p,s ) en S _m (p,s ).

Het machtswetverval van de intensiteit, zoals geformuleerd in Vgl. (22) wordt verkregen na het uitvoeren van het gemiddelde over alle oriëntaties [29]. Bij gelijke waarschijnlijkheid voor elke oriëntatie kan het gemiddelde worden berekend in het geval van tweedimensionale fractals door integratie over alle richtingen van de verstrooiingsvector q =(p,s ):

$$ \langle f(p, s) \rangle =\frac{1}{2\pi} \int_{0}^{2\pi}f(q,\phi)\mathrm{d}\phi, $ $ (25)

waar p =q cosϕ en s =q sinϕ . Dus de verstrooiingsintensiteit I (q ) wordt verkregen als een functie van de modulus van impulsoverdracht q ≡|q |.

Omdat, uit de definitie van structuurfactor, men heeft $S_{m}(0)~=~N_{m}^{2}$, waarbij N _m is het aantal vierkanten, zoals gedefinieerd in Vgl. (13), de standaardprocedure voor normalisatie S _m (0) =1 kan worden overgenomen, zoals beschreven in [11, 29].

De resultaten berekend voor de monodisperse verstrooiingsintensiteit I _m (q ) en structuurfactor S _m (q ), met m =6, worden weergegeven in Fig. 2 voor de klassieke vetfractal (f =1 in Fig. 2 a) en, voor het uitgebreide vetfractale model ontwikkeld in dit werk (f =10 in afb. 2 b). Om de figuur 2 b te verkrijgen, hebben we h . overwogen =3 zodat de schaalfactor $\beta _{\mathrm {s}}^{(1)}$ van de eerste drie iteraties constant werd gehouden, daarna had het een andere constante waarde $\beta _{\ mathrm {s}}^{(2)}$ voor de volgende drie iteraties. Zoals verwacht, in beide gevallen (voor f =1 en f =10), kunnen de verschillen tussen de verstrooiingsintensiteit enerzijds en de structuurfactor anderzijds worden waargenomen als $q \gtrsim 1/l_{m}$. In dit gebied heeft de verstrooiingsintensiteit een machtswet-verval I (q )∝q ⁻³ . De structuurfactor heeft een asymptotische waarde die neigt naar 1/N _m , weergegeven door de horizontale lijn in Fig. 2a of de onderste horizontale lijn in Fig. 2b [29, 33].

Een opeenvolging van twee algemene vervalsing van de machtswet, herkenbaar als een superpositie van maxima en minima, over een eenvoudig verval van de machtswet, is te zien in figuur 2a. Maar in Fig. 2b, een gebied van ongeveer constante intensiteit, in het domein 20≲ql ₀ ≲ 100, kan duidelijk worden onderscheiden, omvat door de twee opeenvolgende veralgemeende vervalsingen van de machtswet. Dit komt door de afname van de grootte van de vierkanten met één orde van grootte (f =10) vergeleken met de afstanden ertussen. Dit gebied, waarneembaar rond de bovenste horizontale lijn in figuur 2b, heeft de asymptoot 1/N ₃ , hetzelfde als die van de klassieke vetfractal-structuurfactor, die een gedrag vertoont dat vergelijkbaar is met het geval waarbij alleen de eerste drie iteraties worden beschouwd.

Bovendien is in figuur 2 te zien dat het aantal minima op elke schaal samenvalt met het aantal constante schaalfactoriteraties. Deze minima treden op wanneer de straling die door verschillende vierkanten in de fractal gaat, interfereert en in fase-oppositie is, en dus de meest voorkomende afstanden tussen het midden van vierkanten (2u _m ) zijn gelijk aan π /q . Dit is de reden waarom de geschatte posities van de minima worden verkregen uit de relatie:

$$ q_{i} \simeq \frac{\pi}{2 u_{i}},~~~~i=1, \cdots, m $$ (26)

aangegeven in Fig. 2 door verticale lijnen. Voor de eerste zes iteraties neemt men een vrij goede overeenkomst waar tussen de posities berekend met behulp van Vgl. (26) en die gevonden in de verstrooiingsintensiteit of structuurfactor. Deze benadering kan minder nauwkeurig zijn voor hogere iteraties, zodra het iteratiegetal boven een bepaalde waarde stijgt, omdat in deze gevallen steeds meer afstanden vergelijkbaar zijn met de meest voorkomende afstand. Niettemin zal deze benadering in de praktijk redelijk goed werken, waar men nauwelijks kan verwachten meer dan vier of vijf van dergelijke minima te onderscheiden.

Voor elke individuele schaal, in een bepaald bereik 1/(2u _ik )≲q ≲1/(2u _{ik +1} ), wordt het diffractiepatroon geproduceerd door de interferentie van alleen de i de fractale iteratie. Dit kan worden gebruikt om aan te tonen dat, binnen dit interval, de functies I _m (q )q ^D en S _m (q )q ^D zijn log-periodiek [29], waarbij D is de fractale dimensie die overeenkomt met een gegeven schaal. In het bijzonder voor de resultaten getoond in Fig. 2 en 3, de functies I _m (q )q ^−1.1 en S _m (q )q ^−1.1 zijn log-periodiek met de periode $1/\beta _{\mathrm {s}}^{(1)}$ voor de eerste drie iteraties, terwijl I _m (q )q ^−1,51 en S _m (q )q ^−1,51 zijn log-periodiek met $1/\beta _{\mathrm {s}}^{(2)}$ voor de tweede groep van drie iteraties.

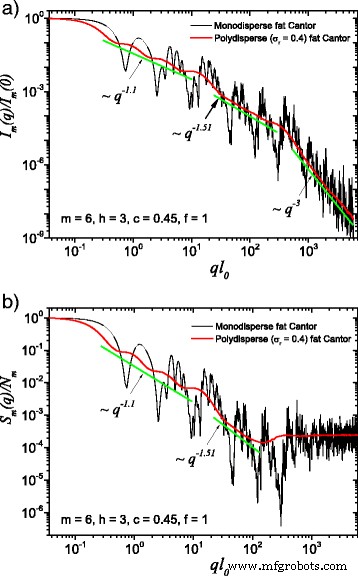
(Kleur online) Een vergelijking tussen monodisperse en polydisperse systemen:a verstrooiingsintensiteit (Vgl. (22)); b structuurfactor (Vgl. (24)), gemiddeld over alle oriëntaties van de fractal, volgens Vgl. (25). Hier, f =1, m =6, h =3 (d.w.z. de schaalfactor wordt gedurende drie opeenvolgende iteraties constant gehouden), en de basisvorm is een vierkant met initiële randlengte l ₀ =l _in . Voor beide gevallen vervaagt de polydispersiteit monodisperse verstrooiingscurven en kunnen de fractale dimensies op elk structureel niveau worden teruggevonden

Op een vergelijkbare manier als deterministische massafractalen, Vgl. (26) kan worden gebruikt om verschillende structurele parameters te verkrijgen die vetfractalen kenmerken. Ten eerste valt het totale aantal minima samen met het totale aantal fractale iteraties. Figuur 2 laat zien dat de fractal bestaat uit drie iteraties met schaalfactor $\beta _{\mathrm {s}}^{(1)}$ en drie iteraties met schaalfactor $\beta _{\mathrm {s} }^{(2)}$. Ten tweede, uit de periodiciteit van deze minima (of uit de periodiciteit van I _m (q )q ^D en S _m (q )q ^D ), kunnen de schaalfactoren worden hersteld. In Fig. 2b kan de schaalfactor $\beta _{\mathrm {s}}^{(1)}$ worden verkregen uit de periodiciteit van minima bij ql ₀ ≃7,25 en 90, terwijl de schaalfactor $\beta _{\mathrm {s}}^{(2)}$ kan worden verkregen uit de periodiciteit van minima bij ql ₀ ≃ 400, 1000 en 2500. Bovendien kan de lengte van het tussenplateau tussen fractale gebieden worden gebruikt als een indicatie van de verhouding (f ) van afstanden tussen verstrooiingseenheden en hun totale grootte. In Fig. 2b komt dit bereik overeen met 13≲ql ₀ ≲130.

Intensiteit en structuurfactor polydisperse verstrooiing

In dit deel van ons werk kunnen we er nu rekening mee houden dat de roostergroottes een distributiefunctie gehoorzamen D _N (l ₀ ), zo gedefinieerd dat D _N (l ₀ )dl ₀ geeft de kans dat de grootte van het fractale rooster in het interval ligt (l ₀ ,ik ₀ +dl ₀ ). Deze stap introduceert polydispersiteit in ons vetfractal-model. We illustreren dit door een log-normale verdeling te kiezen:

$$ D_{\mathrm{N}}(l_{0}) =\frac{1}{\sigma l_{0} (2\pi)^{1/2}}e^{-\frac{\left (\log(l_{0}/\mu)+\sigma^{2}/2\right)^{2}}{2\sigma^{2}}}, $$ (27)

met relatieve variantie $\sigma _{\mathrm {r}} =\left (\left \langle l_{0}^{2} \right \rangle _{D} - \mu ^{2}\right)^ {1/2}/\mu $, gemiddelde waarde μ =〈l ₀ 〉_D , and variance $\sigma =\left (\log \left (1+\sigma _{\mathrm {r}}^{2}\right)\right)^{1/2}$. Using Eqs. (21) and (27) one obtains the polydisperse intensity averaged over the distribution function:

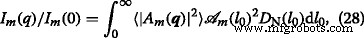
waar is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term 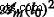[29].

The computed results in the case of polydisperse (red curves) and monodisperse (black curves) scattering intensities (labeled by a) and structure factors (labeled by b) can be seen in Figs. 3 and 4. The difference between them is given by the value of the f factor. In Fig. 3, the classical construction of a fat fractal was used so that f =1, while taking into account the smaller sizes of the basic units leads to the choice of f =10 in Fig. 4. Polydispersity is calculated for a relative variance of σ _r =0.4. It can be seen that the oscillations are smeared out, the overall amplitude decreases, so that the scattering curves become smoother [29, 40]. However, for this particular value of σ _r , the positions of main minima and maxima are still observable.

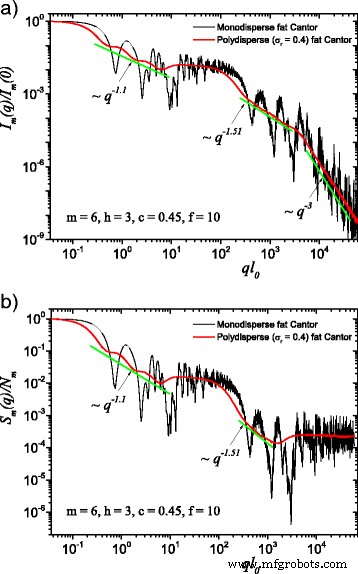
(Color online) A comparison between monodisperse and polydisperse systems:a scattering intensity (Eq. (22)); b structure factor (Eq. (24)), averaged over all orientations of the fractal, according to Eq. (25). Here, f =10 (and thus, a region of constant intensity appears at about 20≲ql ₀ ≲100), m =6, h =3 (i.e., the scaling factor is kept constant for three consecutive iterations), and the basic shape is a square of initial edge length l ₀ =l _in . For both cases, the polydispersity smears out monodisperse scattering curves, and the fractal dimensions can be recovered at each structural level

More generally, for small values of σ _r (i.e., small enough that the oscillations are observable), the estimation given by Eq. (26) can be still used. Hence, the number of fractal iterations, the scaling factor at each structural level, the ratio of the distances between scattering units, and their overall size can be recovered. When σ _r is increased to high enough values so that oscillations are completely smeared out, the scattering curves become simple power-law decays. Since we used a narrow bell-shaped distribution, the scattering exponent is preserved. Moreover, it gives, for each power-law decay, the fractal dimension of that particular structural level. This is in good agreement with the theoretical estimation of Eq. (14). This is also in accordance with experimental setups, where almost every scattering curve has a certain degree of polydispersity. Thus, our developed fat fractal model, with an interleaved region of constant intensity, recovers the fractal dimension at each structural level from polydisperse experimental data.

Conclusions

In this article, we suggest a theoretical model that generalizes the standard one for nanoscale fat fractals. It is characterized by the fact that the initial edge size of the elementary unit shape is taken to be much smaller than that of the overall size of the fractal, and thus, much smaller than the distances between the elementary units inside the fractal. Figure 1 b illustrates the basic model, when a quotient of 1/2 is considered in-between these quantities, respectively.

Based on this model, an analytical formula is calculated and presented, in Eq. (22) for the scattering intensity and in Eq. (24) for the structure factor. Averaging over all possible orientations is done according to Eq. (25). These averaged quantities are characterized, on a double logarithmic scale, by the presence of two structural levels, and thus by two power-law decays interleaved by a region of constant intensity, represented by a plateau, as seen in Figs. 2 b and 4. This plateau coincides with the asymptotic region of the structure factor of the fat fractal, as if we would have considered only the contribution from the first structural level, when the scaling factor was kept constant. The asymptotic values of the plateaus can be used to obtain the number of scattering units for each structural level. The length of the plateau is controlled by the value of f . The power-law decays encompassing the plateau are obtained by keeping constant the scaling factors for a finite number of iterations, in our case, as an example, for three out of a total of six. The slope of the second power-law decay is higher because the values of scaling factors, by definition, increase at each structural level, and this is confirmed by our numerical computations, as can be seen in Figs. 2, 3, and 4.

We also described the polydisperse case of the fat fractal model. Here, the sizes of the composing units obey, as an example, a log-normal distribution function. We obtained smoothed curves for the scattering intensities and structure factors. The monodisperse scattering curves as well as the polydisperse ones, with small enough values of the relative variance, allow to obtain the scaling factors at each structural level, while the scattering exponents in the polydisperse curve give the fractal dimensions at each structural level. The chosen value of 0.4 for the relative variance is meant to illustrate the case in which one can still observe some minima in the scattering characteristics, and the curves still retain a shape close to power-law decays.

The results obtained in the framework of the suggested model can be used to reveal structural properties of fractal materials characterized by a regular law of changing of the fractal dimensions. The proposed model is also a very versatile one because it can be extended to include other features such as different shapes of the elementary unit, more than two structural levels, or it can be adapted to work in other Euclidean dimensions. These results are useful for a detailed description of experimental diffraction data in the context of small-angle scattering obtained from various complex nano- and micro- scaled hierarchical structures.

Appendix

fractal dimension

Mass and, respectively, surface fractal dimensions are probably the most important quantities that characterize a fractal. Actually, we will deal only with deterministic mass fractals, and we shall refer to mass fractal dimension, simply as the fractal dimension (D _m ).

In general terms, the mass-radius relation can be rewritten as [2]:

$$ M(r) =A(r) r^{D_{\mathrm{m}}}, $$ (29)

where the scaling law correction A (r ) tends to a constant value if r →∞ .

If it is known a priori that the structure is a fractal in the high number limit, the fractal dimension can be found straight from the first iteration. To illustrate this procedure, let us consider a fractal of size l ₀ , composed of k elementary units at the first iteration, each of size β _s l ₀ , where β _s is a scaling factor. Since the mass-radius relation, given by Eq. (29), is equivalent with the scale-invariance relation [2]:

$$ M(\beta_{\mathrm{s}}l_{0}) =\beta_{\mathrm{s}}^{D_{\mathrm{m}}}M(l_{0}), $$ (30)

one can write M (l ₀ )=kM (β _s l ₀ ). Vergelijking gebruiken (29), one obtains a direct method to compute the fractal dimension, via:

$$ k \beta_{\mathrm{s}}^{D_{\mathrm{m}}} =1. $$ (31)

fraunhofer diffraction and the array theorem

Let us consider a two-dimensional diffracting aperture Σ , laid in the (x,y ) plane, illuminated in the positive z direction. In an observation plane (u,v ), parallel to Σ , the complex-valued amplitude of the obtained diffraction image, computed using the framework of scalar theory of diffraction, according to the Huygens-Fresnel principle, can be written as [41]:

$$ A(u,v) =\frac{z}{i\lambda} \iint\limits_{\Sigma} A(x,y)\frac{e^{ikr}}{r^{2}} \mathrm{d} x\,\mathrm{d} y. $$ (32)

In the previous formula, $r =\sqrt {z^{2}+(u-x)^{2}+(v-y)^{2}}$ is the distance between two arbitrarily points taken, respectively, from the plane containing Σ and from the observation plane. For the Fraunhofer diffraction model to be applicable, this distance must satisfy the condition of being much bigger than the wavelength λ .

Performing a binomial expansion of the square root in Eq. (32) and retaining only the first two terms, one obtains [41]:

$$ r \approx z\left(1 + \frac{(u-x)^{2}}{2z^{2}} + \frac{(v-y)^{2}}{2z^{2}}\right). $$ (33)

This approximation leads to the Fresnel diffraction integral:

$$ \frac{A(u,v)}{P(u,v)} =\iint\limits_{-\infty}^{~~~+\infty} \left\{A(x,y) e^{i\frac{k}{2z}(x^{2} + y^{2})}\right\} e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y, $$ (34)

where the prefactor P (u,v ) is given by

$$ P(u,v) =\frac{e^{ikz}e^{i\frac{k}{2z}(u^{2}+v^{2})}}{i\lambda z}, $$ (35)

en k =2π /λ . Considering, in addition, that the condition z ≫k Max(x ² +y ² )/2 is satisfied, one has $\text {Exp}{\left (\frac {k}{2z}(x^{2}+y^{2})\right)} \simeq 1$. Rewriting Eq. (34), the Fraunhofer approximation becomes:

$$ A(u,v) =P(u,v)\iint\limits_{-\infty}^{~~~+\infty} A(x,y) e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y. $$ (36)

Denoting the spatial frequencies with p =u /(λ z ) and s =v /(λ z ) and ignoring the multiplicative phase factor P (u,v ) preceding the integral in Eq. (36), the amplitude becomes simply the Fourier transform of the distribution of the Σ aperture. Considering that the illumination is made using a monochromatic, unit-amplitude plane-wave, at normal incidence, and that the field distribution across the aperture is equal to its transmission function T (x,y ), one obtains the frequency distribution of the diffraction amplitude in the phase space:

$$ A(p,s) =\iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{-2 i \pi (px + sy)}\mathrm{d}x\,\mathrm{d}y. $$ (37)

Dip-coating procestechniek en prestatie-optimalisatie voor drie-staten elektrochrome apparaten Batchfabricage van breedband metalen vlakke microlenzen en hun arrays door zelfassemblage van nanosfeer te combineren met conventionele fotolithografie

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal