Een meerlagig Perceptron neuraal netwerk trainen

We kunnen de prestaties van een Perceptron aanzienlijk verbeteren door een laag verborgen knooppunten toe te voegen, maar die verborgen knooppunten maken de training ook wat ingewikkelder.

Tot dusverre heb je in de AAC-serie over neurale netwerken geleerd over gegevensclassificatie met behulp van neurale netwerken, vooral van de Perceptron-variant.

Bekijk de onderstaande serie of duik in dit nieuwe artikel waarin de basis van het meerlaagse Perceptron (MLP) neurale netwerk wordt uitgelegd.

1. Hoe classificatie uitvoeren met behulp van een neuraal netwerk:wat is de Perceptron?
2. Een eenvoudig Perceptron neuraal netwerkvoorbeeld gebruiken om gegevens te classificeren
3. Een basis Perceptron neuraal netwerk trainen
4. Eenvoudige neurale netwerktraining begrijpen
5. Een inleiding tot trainingstheorie voor neurale netwerken
6. De leersnelheid in neurale netwerken begrijpen
7. Geavanceerde machine learning met de meerlaagse Perceptron
8. De Sigmoid-activeringsfunctie:activering in meerlaagse Perceptron neurale netwerken
9. Een meerlagig Perceptron neuraal netwerk trainen
10. Trainingsformules en backpropagation voor meerlaagse perceptrons begrijpen
11. Neurale netwerkarchitectuur voor een Python-implementatie
12. Hoe maak je een meerlaags Perceptron neuraal netwerk in Python
13. Signaalverwerking met behulp van neurale netwerken:validatie in neuraal netwerkontwerp
14. Trainingsdatasets voor neurale netwerken:een neuraal netwerk met Python trainen en valideren

Wat is een meerlagig Perceptron neuraal netwerk?

Het vorige artikel toonde aan dat een enkellaagse Perceptron simpelweg niet het soort prestaties kan leveren dat we verwachten van een moderne neurale netwerkarchitectuur. Een systeem dat beperkt is tot lineair scheidbare functies zal niet in staat zijn om de complexe input-outputrelaties te benaderen die voorkomen in real-life signaalverwerkingsscenario's. De oplossing is een meerlaagse Perceptron (MLP), zoals deze:

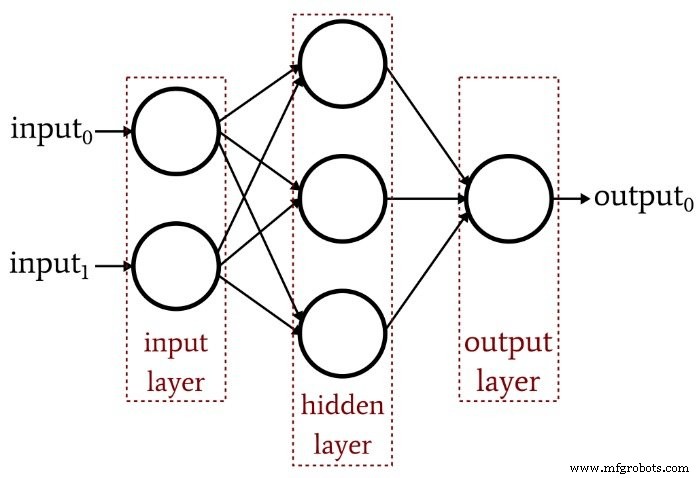
Door die verborgen laag toe te voegen, veranderen we het netwerk in een "universele benadering" die een uiterst geavanceerde classificatie kan bereiken. Maar we moeten altijd onthouden dat de waarde van een neuraal netwerk volledig afhankelijk is van de kwaliteit van de training. Zonder overvloedige, diverse trainingsgegevens en een effectieve trainingsprocedure, zal het netwerk nooit "leren" inputvoorbeelden te classificeren.

Waarom bemoeilijkt de verborgen laag training?

Laten we eens kijken naar de leerregel die we in een vorig artikel hebben gebruikt om een ​​enkellaagse Perceptron te trainen:

\[w_{new} =w+(\alpha\times(output_{expected}-output_{calculated})\times input)\]

Let op de impliciete aanname in deze vergelijking:we werken de gewichten bij op basis van de waargenomen uitvoer, dus om dit te laten werken, moeten de gewichten in de enkellaagse Perceptron de uitvoerwaarde rechtstreeks beïnvloeden. Het is alsof je de temperatuur van kraanwater kiest door aan de twee knoppen voor warm en koud te draaien. De relatie tussen de algehele temperatuur en de werking van de knop is vrij eenvoudig, en zelfs mensen die niet van wiskunde houden, kunnen de gewenste watertemperatuur vinden door een tijdje aan de knoppen te prutsen.

Maar stel je nu voor dat de stroming van water door de warme en koude leidingen op een complexe, zeer niet-lineaire manier verband houdt met de positie van de knop. Je draait gestaag en langzaam aan de knop voor warm water, maar het resulterende debiet varieert grillig. Je probeert de knop voor koud water en het doet hetzelfde. Onder deze omstandigheden de ideale watertemperatuur bepalen, vooral omdat de "output" moet worden bereikt door een combinatie van twee verwarrende regelrelaties, zou veel moeilijker zijn.

Zo begrijp ik het dilemma van de verborgen laag. De gewichten die de invoerknooppunten verbinden met de verborgen knooppunten zijn conceptueel analoog aan die mechanisch grillige knoppen - omdat invoer-naar-verborgen gewichten geen direct pad naar de uitvoerlaag hebben, is de relatie tussen deze gewichten en de uitvoer van het netwerk zo complex dat de hierboven getoonde eenvoudige leerregel niet effectief zal zijn.

Een nieuw trainingsparadigma

Aangezien de oorspronkelijke leerregel van Perceptron niet kan worden toegepast op netwerken met meerdere lagen, moeten we onze trainingsstrategie heroverwegen. Wat we gaan doen is gradiëntafdaling opnemen en een foutfunctie minimaliseren.

Een ding om in gedachten te houden is dat deze trainingsprocedure niet specifiek is voor meerlaagse neurale netwerken. Gradiëntafdaling komt uit de algemene optimalisatietheorie en de trainingsprocedure die we gebruiken voor MLP's is ook van toepassing op enkellaagse netwerken. Echter, zoals ik het begrijp, is MLP-stijl gradiëntafdaling (althans theoretisch) niet nodig voor een Perceptron met één laag, omdat de eenvoudigere regel die hierboven is weergegeven, uiteindelijk de klus zal klaren.

Het afleiden van de feitelijke gewicht-update-vergelijkingen voor een MLP omvat enige intimiderende wiskunde die ik op dit moment niet intelligent zal proberen uit te leggen. Mijn doel voor de rest van dit artikel is om een ​​conceptuele introductie te geven van twee belangrijke aspecten van MLP-training - gradiëntafdaling en de foutfunctie - en dan zullen we deze discussie in het volgende artikel voortzetten door een nieuwe activeringsfunctie op te nemen.

Gradient afdaling

Zoals de naam al aangeeft, is gradiëntafdaling een middel om af te dalen naar het minimum van een foutfunctie op basis van helling. Het onderstaande diagram geeft de manier weer waarop een gradiënt ons informatie geeft over het wijzigen van gewichten - de helling van een punt op de foutfunctie vertelt ons in welke richting we moeten gaan en hoe ver we verwijderd zijn van het minimum.

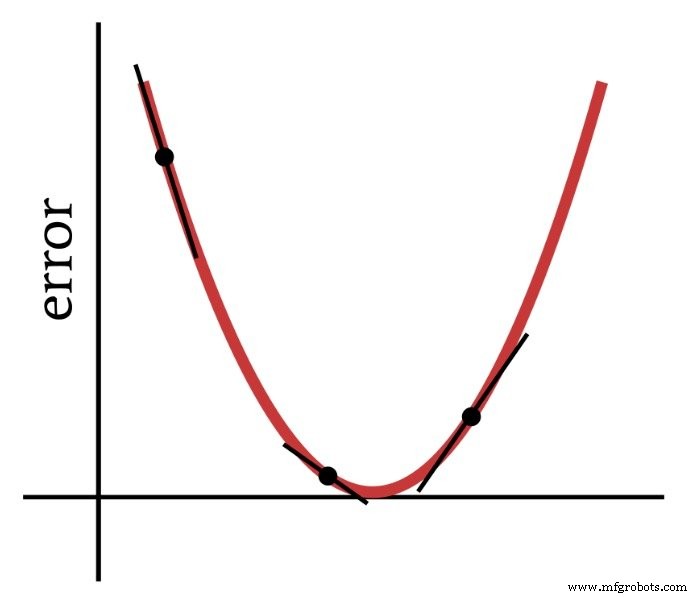
De afgeleide van de foutfunctie is dus een belangrijk element van de berekeningen die we gebruiken om een ​​meerlaagse Perceptron te trainen. Eigenlijk hebben we gedeeltelijk . nodig derivaten hier. Wanneer we gradiëntafdaling implementeren, maken we elke gewichtsaanpassing evenredig met de helling van de foutfunctie met betrekking tot het gewicht dat wordt gewijzigd.

De foutfunctie (AKA-verliesfunctie)

Een veelgebruikte methode om de fout van een neuraal netwerk te kwantificeren, is om het verschil tussen de verwachte (of "doel") waarde en de berekende waarde voor elk uitvoerknooppunt te kwadrateren, en vervolgens al deze gekwadrateerde verschillen op te tellen. Je kunt dit "sum of squared difference" of "summed squared error" of misschien verschillende andere dingen noemen, en je zult ook de afkorting LMS zien, wat staat voor kleinste gemiddelde kwadraat, omdat het doel van training is om het gemiddelde te minimaliseren kwadratische fout. Deze foutfunctie (aangeduid met E) kan wiskundig als volgt worden uitgedrukt:

\[E=\frac{1}{2}\sum_k(t_k-o_k)^2\]

waarbij k het bereik van uitvoerknooppunten aangeeft, t de doeluitvoerwaarde is en o de berekende uitvoerwaarde.

Conclusie

We hebben de basis gelegd voor het succesvol trainen van een meerlaagse Perceptron, en we zullen dit interessante onderwerp verder onderzoeken in het volgende artikel.