De nauwkeurigheid van een neuraal netwerk met verborgen lagen vergroten

In dit artikel zullen we enkele classificatie-experimenten uitvoeren en gegevens verzamelen over de relatie tussen de dimensionaliteit van verborgen lagen en netwerkprestaties.

In dit artikel leert u hoe u een verborgen laag kunt wijzigen om de nauwkeurigheid van het neurale netwerk te verbeteren met behulp van een Python-implementatie en voorbeeldproblemen.

Voordat we echter op dat onderwerp ingaan, overweeg dan om de eerdere artikelen in deze serie over neurale netwerken in te halen:

1. Hoe classificatie uitvoeren met behulp van een neuraal netwerk:wat is de Perceptron?
2. Een eenvoudig Perceptron neuraal netwerkvoorbeeld gebruiken om gegevens te classificeren
3. Een basis Perceptron neuraal netwerk trainen
4. Eenvoudige neurale netwerktraining begrijpen
5. Een inleiding tot trainingstheorie voor neurale netwerken
6. De leersnelheid in neurale netwerken begrijpen
7. Geavanceerde machine learning met de meerlaagse Perceptron
8. De Sigmoid-activeringsfunctie:activering in meerlaagse Perceptron neurale netwerken
9. Een meerlagig Perceptron neuraal netwerk trainen
10. Trainingsformules en backpropagation voor meerlaagse perceptrons begrijpen
11. Neurale netwerkarchitectuur voor een Python-implementatie
12. Hoe maak je een meerlaags Perceptron neuraal netwerk in Python
13. Signaalverwerking met behulp van neurale netwerken:validatie in neuraal netwerkontwerp
14. Trainingsdatasets voor neurale netwerken:een neuraal netwerk met Python trainen en valideren
15. Hoeveel verborgen lagen en verborgen knooppunten heeft een neuraal netwerk nodig?
16. De nauwkeurigheid van een neuraal netwerk met verborgen lagen vergroten

Het aantal knooppunten in een verborgen laag beïnvloedt het classificatievermogen en de snelheid van een neuraal netwerk van Perceptron. We gaan experimenten uitvoeren die ons zullen helpen om een ​​beginnende intuïtie te formuleren over hoe de dimensionaliteit van verborgen lagen past in de poging om een ​​netwerk te ontwerpen dat binnen een redelijke tijd traint, outputwaarden produceert met acceptabele latentie en voldoet aan nauwkeurigheidseisen .

Benchmarking in Python

De Python-code van het neurale netwerk die in deel 12 wordt gepresenteerd, bevat al een sectie die de nauwkeurigheid berekent door het getrainde netwerk te gebruiken om monsters uit een validatiegegevensset te classificeren. We hoeven dus alleen wat code toe te voegen die de uitvoeringstijd voor training (inclusief feedforward-bewerking en backpropagation) en voor de daadwerkelijke classificatiefunctionaliteit (die alleen feedforward-bewerking omvat) rapporteert. We gebruiken de time.perf_counter() functie hiervoor.

Zo markeer ik het begin en het einde van de training:

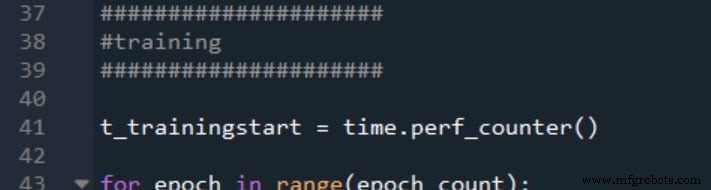
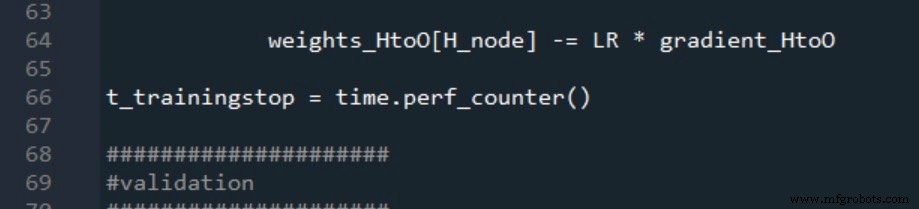
Validatie start- en stoptijden worden op dezelfde manier gegenereerd:

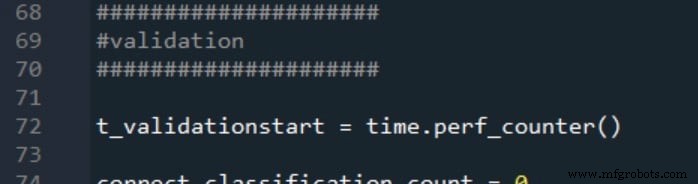
De twee verwerkingstijdmetingen worden als volgt gerapporteerd:

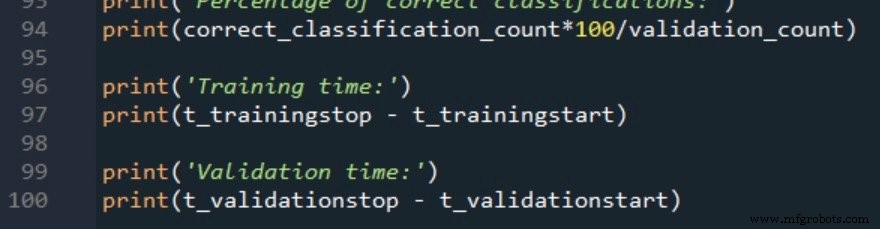
Trainingsgegevens en meetprocedure

Het neurale netwerk zal waar/onwaar-classificatie uitvoeren op invoersamples die bestaan ​​uit vier numerieke waarden tussen –20 en +20.

We hebben dus vier invoerknooppunten en één uitvoerknooppunt en de invoerwaarden worden gegenereerd met de onderstaande Excel-vergelijking.

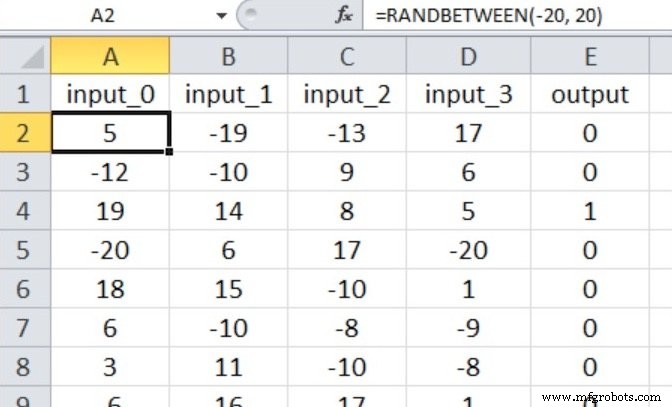
Mijn trainingsgegevensset bestaat uit 40.000 voorbeelden en de validatieset heeft 5000 voorbeelden. De leersnelheid is 0,1 en ik voer slechts één trainingsperiode uit.

We zullen drie experimenten uitvoeren die input-outputrelaties vertegenwoordigen met verschillende gradaties van complexiteit. De np.random.seed(1) verklaring is becommentarieerd, dus de initiële gewichtswaarden zullen variëren en dus ook de nauwkeurigheid van de classificatie.

In elk experiment wordt het programma vijf keer uitgevoerd (met dezelfde trainings- en validatiegegevens) voor elke dimensie van verborgen lagen, en de uiteindelijke metingen voor nauwkeurigheid en verwerkingstijd zijn het rekenkundig gemiddelde van de resultaten die worden gegenereerd door de vijf afzonderlijke runs .

Experiment 1:een probleem met lage complexiteit

In dit experiment is de uitvoer alleen waar als de eerste drie invoer groter is dan nul, zoals weergegeven in de onderstaande Excel-screenshot (merk op dat de vierde invoer geen effect heeft op de uitvoerwaarde).

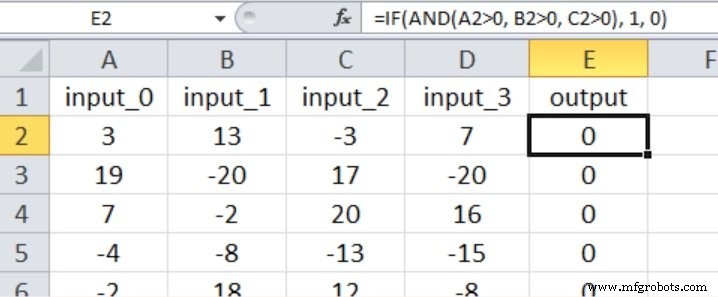
Ik denk dat dit kwalificeert als een vrij eenvoudige input-outputrelatie voor een meerlaagse Perceptron.

Op basis van de aanbevelingen die ik in deel 15 heb gegeven met betrekking tot het aantal lagen en knooppunten dat een neuraal netwerk nodig heeft, zou ik beginnen met een verborgen laag-dimensionaliteit gelijk aan tweederde van de invoer-dimensionaliteit.

Aangezien ik geen verborgen laag kan hebben met een fractie van een knoop, begin ik bij H_dim =2 . De onderstaande tabel geeft de resultaten weer.

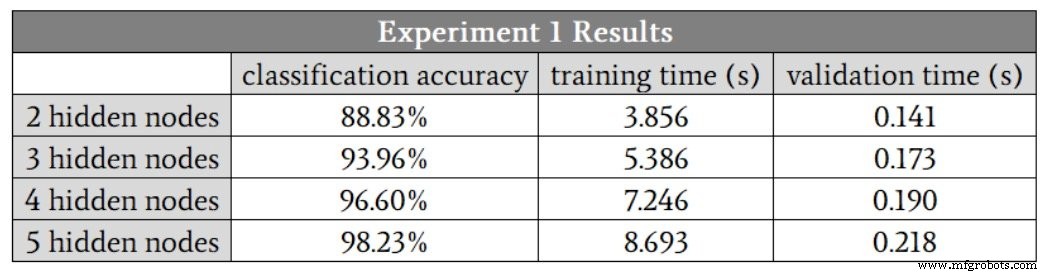
We zien een verbetering van de classificatie tot vijf verborgen knooppunten. Ik denk echter dat deze cijfers het voordeel van een verhoging van vier naar vijf knooppunten overdrijven, omdat de nauwkeurigheid van een van de runs met vier verborgen knooppunten 88,6% was, en dit sleepte het gemiddelde naar beneden.

Als ik die run met lage nauwkeurigheid elimineer, is de gemiddelde nauwkeurigheid voor vier verborgen knooppunten eigenlijk iets hoger dan het gemiddelde voor vijf verborgen knooppunten. Ik vermoed dat in dit geval vier verborgen knooppunten de beste balans tussen nauwkeurigheid en snelheid zullen bieden.

Een ander belangrijk ding om op te merken in deze resultaten is het verschil in hoe de dimensionaliteit van verborgen lagen de trainingstijd en verwerkingstijd beïnvloedt. Door van twee naar vier verborgen knooppunten te gaan, neemt de validatietijd met een factor 1,3 toe, maar de trainingstijd met een factor 1,9.

Training is beduidend meer rekenintensief dan feedforward-verwerking, dus we moeten er speciaal rekening mee houden hoe netwerkconfiguratie ons vermogen beïnvloedt om het netwerk binnen een redelijke tijd te trainen.

Experiment 2:Een matig-complexiteitsprobleem

De Excel-screenshot toont de input-outputrelatie voor dit experiment. Alle vier de inputs hebben nu invloed op de outputwaarde, en de vergelijkingen zijn minder eenvoudig dan in Experiment 1.

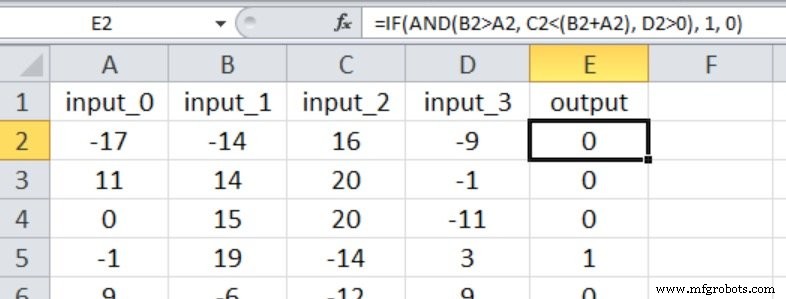
Ik begon met drie verborgen knooppunten. Dit zijn de resultaten:

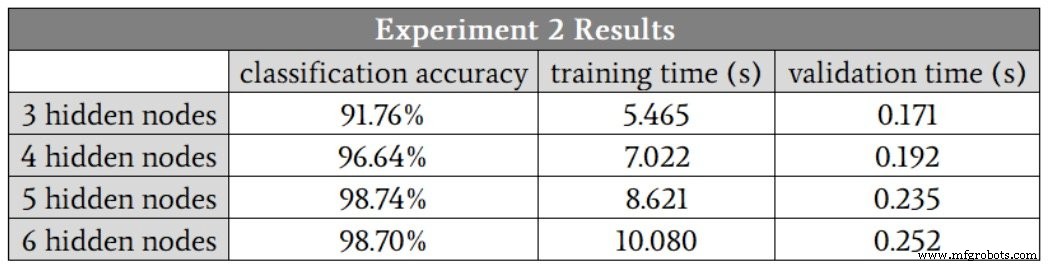
In dit geval vermoed ik dat vijf verborgen knooppunten ons de beste combinatie van nauwkeurigheid en snelheid zullen geven, hoewel de runs met vier verborgen knooppunten opnieuw één nauwkeurigheidswaarde produceerden die aanzienlijk lager was dan de andere. Als u deze uitbijter negeert, lijken de resultaten voor vier verborgen knooppunten, vijf verborgen knooppunten en zes verborgen knooppunten erg op elkaar.

Het feit dat de runs met vijf verborgen knooppunten en zes verborgen knooppunten geen uitschieters genereerden, leidt ons tot een interessante mogelijke bevinding:misschien maakt het vergroten van de dimensionaliteit van de verborgen lagen het netwerk robuuster tegen omstandigheden die om de een of andere reden ervoor zorgen dat training bijzonder moeilijk zijn.

Experiment 3:een probleem met hoge complexiteit

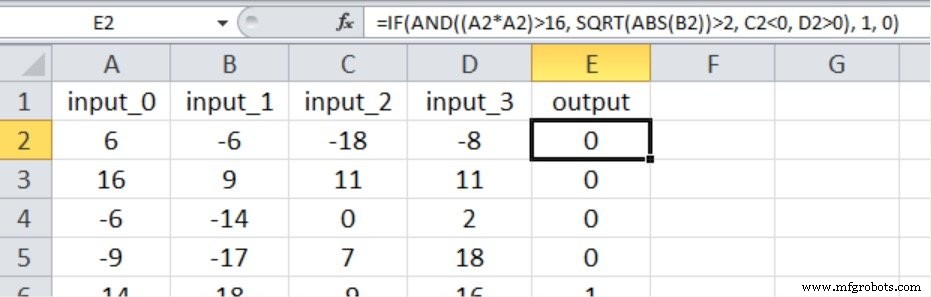
Zoals hieronder wordt getoond, omvat de nieuwe invoer-uitvoerrelatie opnieuw alle vier invoerwaarden, en we hebben niet-lineariteit geïntroduceerd door een van de invoer te kwadrateren en de vierkantswortel van een andere te nemen.

Dit zijn de resultaten:

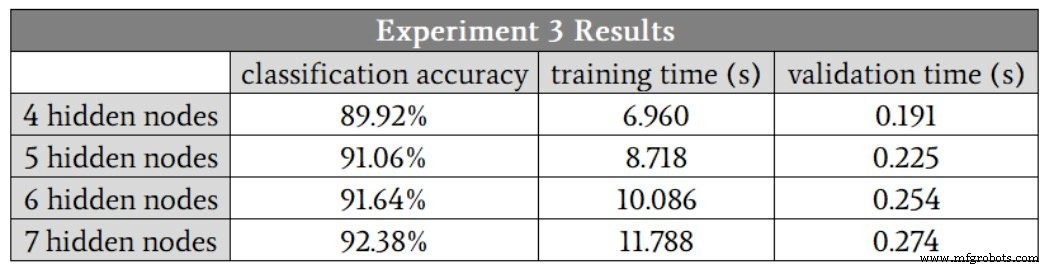
Het netwerk had beslist meer moeite met deze complexere wiskundige relatie; zelfs met zeven verborgen knooppunten was de nauwkeurigheid lager dan wat we bereikten met slechts drie verborgen knooppunten in het probleem met lage complexiteit. Ik ben ervan overtuigd dat we de complexe prestaties kunnen verbeteren door andere aspecten van het netwerk aan te passen, bijvoorbeeld door een bias (zie deel 11) of door het leertempo te verlagen (zie deel 6).

Desalniettemin zou ik de dimensionaliteit van de verborgen laag op zeven houden totdat ik er volledig van overtuigd was dat andere verbeteringen het netwerk in staat zouden kunnen stellen om adequate prestaties te behouden met een kleinere verborgen laag.

Conclusie

We hebben enkele interessante metingen gezien die een vrij duidelijk beeld schetsen van de relatie tussen de dimensionaliteit van verborgen lagen en de prestaties van Perceptron. Er zijn zeker nog veel meer details die we zouden kunnen onderzoeken, maar ik denk dat dit je solide basisinformatie geeft waarop je kunt putten wanneer je experimenteert met het ontwerpen en trainen van neurale netwerken.