Stroom- en spanningswet van Kirchhoff (KCL &KVL) | Opgelost voorbeeld

KCL &KVL – Eerste en tweede wet van Kirchhoff met opgelost voorbeeld

Een Duitse natuurkundige "Robert Kirchhoff" introduceerde in 1847 twee belangrijke elektrische wetten waarmee we gemakkelijk de equivalente weerstand van een complex netwerk en stromende stromen in verschillende geleiders kunnen vinden. Zowel AC- als DC-circuits kunnen worden opgelost en vereenvoudigd door gebruik te maken van deze eenvoudige wetten die bekend staan ​​als de stroomwet van Kirchhoff (KCL) en de spanningswet van Kirchhoff (KVL).

Houd er rekening mee dat KCL is afgeleid van de ladingscontinuïteitsvergelijking in elektromagnetisme, terwijl KVL is afgeleid van de Maxwell - Faraday-vergelijking voor statisch magnetisch veld (de afgeleide van B met betrekking tot tijd is 0 ).

Kirchhoffs huidige wet (KCL):

Volgens KCL:

In elk elektrisch netwerk is de algebraïsche som van inkomende stromen naar een punt en uitgaande stromen vanaf dat punt nul. Of de inkomende stromen naar een punt zijn gelijk aan de uitgaande stromen van dat punt.

Met andere woorden, de som van de stromen die naar een punt stromen, is gelijk aan de som van de stromen die er vanaf stromen. Of de algebraïsche som van de stromen die een knoop binnenkomen, is gelijk aan de algebraïsche som van de stromen die de knoop verlaten.

Uitleg van KCL:

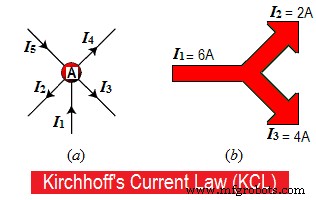
Stel dat sommige geleiders elkaar ontmoeten op een punt "A", zoals weergegeven in figuur 1.a. In sommige geleiders komen stromen binnen naar het punt "A", terwijl in andere geleiders stromen vertrekken of uitgaan van punt "A".

Beschouw de inkomende of binnenkomende stromen als "positief (+) naar punt "A", terwijl de uitgaande of uitgaande stromen van punt "A" "Negatief (-)" zijn.
dan:

Ik ₁ + (–Ik ₂ ) + (–Ik ₃ ) + (–Ik ₄ ) + Ik ₅ =0

OF

Ik ₁ + Ik ₅ – Ik ₂ – Ik ₃ – Ik ₄ =0

OF

Ik ₁ + Ik ₅ =Ik ₂ + Ik ₃ + Ik ₄ =0

d.w.z.

Inkomende of binnenkomende stromingen =uitgaande of uitgaande stromingen

Of

ΣIk Invoeren =ΣI Vertrek

Zo komt 8A naar een punt toe en 5A plus 3A verlaten dat punt in fig. 1.b, daarom

8A =5A + 3A

8A =8A.

Kirchhoff's Voltage Law (KVL):

De tweede wet van Kirchhoff of KVL stelde dat;

Met andere woorden, in elke gesloten lus (ook bekend als Mesh), is de algebraïsche som van de toegepaste EMF gelijk aan de algebraïsche som van de spanningsdalingen in de elementen . De tweede wet van Kirchhoff staat ook bekend als de spanningswet of de maaswet.

ΣIR=ΣE

Uitleg van KVL:

In fig. wordt een gesloten circuit getoond met twee aansluitingen van batterijen E₁ en E₂ . De totale som van E.M.F's van de batterijen wordt aangegeven met E₁ -E₂ . De denkbeeldige stroomrichting wordt ook weergegeven in de afbeelding.

E₁ drijft de stroom in een richting die positief zou moeten zijn, terwijl E₂ interfereert in de richting van de stroom (d.w.z. het is in de tegenovergestelde richting van de veronderstelde stroomrichting), daarom wordt het als negatief beschouwd. De spanningsval in dit gesloten circuit hangt af van het product van spanning en stroom.

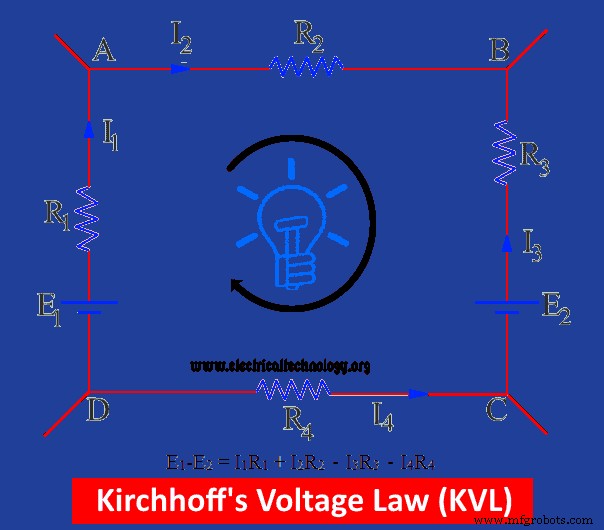
De spanningsval treedt op in de veronderstelde richting van de stroom staat bekend als positieve spanningsval, terwijl de andere een negatieve spanningsval is.

In de bovenstaande afbeelding, I₁ R₁ en ik₂ R₂ zijn positieve spanningsdalingen en I₃ R₃ en ik₄ R₄ zijn negatieve V.D.

Als we rond het gesloten circuit (of elke mesh) gaan en de weerstand van de geleider en de stroom erin vermenigvuldigen, dan is de som van de IR gelijk aan de som van de toegepaste EMF-bronnen die op het circuit zijn aangesloten.

De algemene vergelijking voor het bovenstaande circuit is:

E₁ – E₂ =ik ₁ R₁ + ik ₂ R₂ – ik ₃ R₃ – ik ₄ R₄

Als we in de veronderstelde richting van de stroom gaan zoals getoond in de figuur, dan wordt het product van de IR als positief genomen, anders negatief.

Goed om te weten:

Stroomrichting:

Het is erg belangrijk om de richting van de stroom te bepalen bij het oplossen van circuits via de wetten van Kirchhoff. Hetzelfde als het geval van verkiezingsstroom en conventionele stroom.

De richting van de stroom kan met de klok mee of tegen de klok in worden aangenomen. Nadat u de aangepaste richting van de stroom hebt geselecteerd, moet u dezelfde richting voor het totale circuit toepassen en behouden tot de definitieve oplossing van het circuit.

Als we de uiteindelijke waarde als positief hebben gezien, was de veronderstelde richting van de stroom correct. In het geval van negatieve waarden, wordt de stroom van de richting omgekeerd in vergelijking met de veronderstelde dan.

Circuitanalyse volgens de wetten van Kirchhoff

Opgelost voorbeeld op KCL en KVL (de wetten van Kirchhoff)

Voorbeeld:

Weerstanden van R₁ =10Ω, R₂ =4Ω en  R₃ =8Ω zijn aangesloten op maximaal twee batterijen (met verwaarloosbare weerstand) zoals weergegeven. Zoek de stroom door elke weerstand.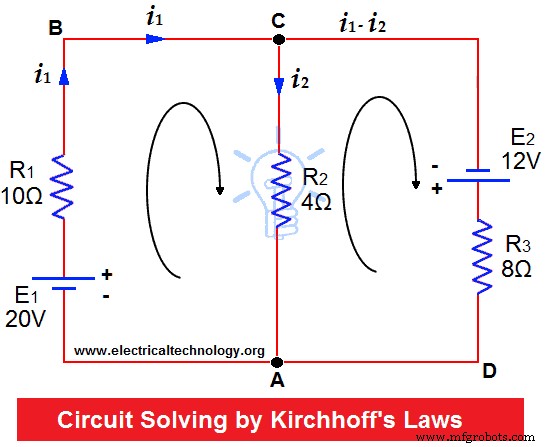

Oplossing:

Veronderstel dat stromingen stromen in richtingen die worden aangegeven door pijlen.

KCL toepassen op knooppunten C en A.

Daarom, stroom in mesh ABC =i ₁

Huidige in Mesh CA =i ₂

Vervolgens actueel in Mesh CDA =i ₁ – ik ₂

Toepassen KVL op Mesh ABC, 20V werkt met de klok mee. Als we de som van IR-producten gelijkstellen, krijgen we;

10i ₁ + 4ik ₂ =20   …   (1)

In mesh ACD werkt 12 volt met de klok mee, dan:

8(i ₁ – ik ₂ ) – 4ik ₂ =12

8i ₁ – 8ik ₂ – 4ik ₂ =12

8i ₁ – 12ik ₂ =12   …   (2)

Vergelijking (1) vermenigvuldigen met 3;

30i ₁ + 12ik ₂ =60

Oplossen voor i ₁

30i ₁ + 12ik ₂ =60

8i ₁ – 12ik ₂ =12

___________
38i ₁ =72

De bovenstaande vergelijking kan ook worden vereenvoudigd door Eliminatie of de regel van Cramer.

i ₁ =72 ÷ 38 =1.895 Ampère =Stroom in weerstand van 10 Ohm

Als we deze waarde in (1) vervangen, krijgen we:

10 (1.895) + 4i ₂ =20

4i ₂ =20 – 18,95

i ₂ =0,263 Ampère =Stroom in weerstanden van 4 Ohm.

Nu,

i ₁ – ik ₂ =1.895 – 0.263 =1.632 Ampere

Toepassingen van de wetten van Kirchhoff

• De wetten van Kirchhoff kunnen worden gebruikt om de waarden van onbekende waarden zoals stroom en spanning te bepalen, evenals de richting van de stromende waarden van deze kwintetten in het circuit.
• Deze wetten kunnen worden toegepast op elk circuit* (zie de beperking van de wetten van Kirchhoff aan het einde van het artikel), maar nuttig om de onbekende waarden in complexe circuits en netwerken te vinden.
• Ook gebruikt in Nodal- en Mesh-analyse om de waarden van stroom en spanning te vinden.
• Stroom door elke onafhankelijke lus wordt gedragen door KVL (elke lus) toe te passen en stroom in elk element van een circuit door alle stroom te tellen (van toepassing in de lusstroommethode).
• De stroom door elke vertakking wordt gedragen door KCL (elk knooppunt) KVL toe te passen in elke lus van een circuit (van toepassing in de lusstroommethode).
• De wetten van Kirchhoff zijn nuttig om de overdracht van energie door een elektrisch circuit te begrijpen.

Goed om te weten:

Met deze vuistregels moet rekening worden gehouden bij het vereenvoudigen en analyseren van elektrische circuits volgens de wetten van Kirchhoff:

• De spanningsdaling in een lus als gevolg van stroom met de klok mee wordt beschouwd als een positieve (+) spanningsdaling.
• De spanningsval in een lus als gevolg van stroom tegen de klok in wordt beschouwd als een negatieve (-) spanningsval.
• De stroom die de batterij in wijzerzin afleidt, wordt als positief (+) beschouwd.
• De stroom die de batterij tegen de klok in afleidt, wordt als positief (-) beschouwd.

Beperkingen van de wetten van Kirchhoff:

• KCL is toepasbaar in de veronderstelling dat er alleen stroom vloeit in geleiders en draden. Terwijl in hoogfrequente circuits waar parasitaire capaciteit niet langer kan worden genegeerd. In dergelijke gevallen kan stroom in een open circuit vloeien omdat in deze gevallen geleiders of draden als transmissielijnen fungeren.
• KVL is van toepassing in de veronderstelling dat er geen fluctuerend magnetisch veld is dat de gesloten lus verbindt. Hoewel, in aanwezigheid van veranderend magnetisch veld in hoogfrequente AC-circuits met korte golflengte, het elektrische veld geen conservatief vectorveld is. Het elektrische veld kan dus niet de gradiënt van een potentiaal zijn en de lijnintegraal van het elektrische veld rond de lus is niet nul, wat rechtstreeks in tegenspraak is met KVL. Daarom is KVL in een dergelijke toestand niet van toepassing.
• Tijdens de overdracht van energie van het magnetische veld naar het elektrische veld, waar fudge moet worden geïntroduceerd in KVL om de P.d (potentiële verschillen) rond het circuit gelijk te maken aan 0.

Verwante berichten over stellingen over de analyse van elektrische circuits:

• Thevenin's Theorema. Stap voor stap procedure met opgelost voorbeeld
• De stelling van Norton. Eenvoudige stapsgewijze procedure met voorbeeld (beeldweergaven)
• SUPERNODE Circuitanalyse | Stap voor stap met opgelost voorbeeld
• SUPERMESH Circuitanalyse | Stap voor stap met opgelost voorbeeld
• Maximale vermogensoverdrachtstelling voor AC- en DC-circuits
• Compensatiestelling – Bewijs, uitleg en opgeloste voorbeelden
• Substitutiestelling – Stapsgewijze handleiding met opgelost voorbeeld
• Theorema van Millman - AC- en DC-circuits analyseren - voorbeelden
• Superpositiestelling – Circuitanalyse met opgelost voorbeeld
• stelling van Tellegen - Opgeloste voorbeelden &MATLAB-simulatie
• Voltage Divider Rule (VDR) - Opgeloste voorbeelden voor R-, L- en C-circuits
• Current Divider Rule (CDR) - Opgeloste voorbeelden voor AC- en DC-circuits
• De wet van Ohm:eenvoudige uitleg met stelling en formules
• Conversie van ster naar delta en van delta naar ster. Y-Δ Transformatie