Wederzijdse inductie en basisbediening

Gedrag van inductoren gewikkeld rond een geleidende kern

Stel dat we een spoel van geïsoleerde draad rond een lus van ferromagnetisch materiaal zouden wikkelen en deze spoel zouden voeden met een wisselspanningsbron:(figuur hieronder (a))

Geïsoleerde wikkeling op de ferromagnetische lus heeft inductieve reactantie, wat de wisselstroom beperkt

Als inductor zouden we verwachten dat deze spoel met ijzeren kern zich verzet tegen de aangelegde spanning met zijn inductieve reactantie, waardoor de stroom door de spoel wordt beperkt zoals voorspeld door de vergelijkingen:

X_L =2πfL en I=E/X (of I=E/Z)

Voor dit voorbeeld moeten we echter de interacties van spanning, stroom en magnetische flux in het apparaat gedetailleerder bekijken.

De spanningswet van Kirchhoff beschrijft hoe de algebraïsche som van alle spanningen in een lus gelijk moet zijn aan nul. In dit voorbeeld zouden we deze fundamentele wet van elektriciteit kunnen toepassen om de respectievelijke spanningen van de bron en van de inductorspoel te beschrijven.

Hier, zoals in elk circuit met één bron en één belasting, moet de spanning die over de belasting valt gelijk zijn aan de spanning die door de bron wordt geleverd, ervan uitgaande dat de nulspanning samenvalt met de weerstand van eventuele verbindingsdraden.

Met andere woorden, de belasting (inductorspoel) moet een tegengestelde spanning produceren die even groot is als de bron, zodat deze kan balanceren met de bronspanning en een algebraïsche lusspanningssom van nul kan produceren.

Waar komt deze tegenspanning vandaan? Als de belasting een weerstand zou zijn (figuur hierboven (b)), komt de spanningsval voort uit verlies van elektrische energie, de "wrijving" van ladingsdragers die door de weerstand stromen.

Bij een perfecte spoel (geen weerstand in de spoeldraad) komt de tegenspanning van een ander mechanisme:de reactie tot een veranderende magnetische flux in de ijzeren kern. Wanneer wisselstroom verandert, verandert flux Φ. Veranderende flux induceert een tegen-EMF.

Relatie tussen spanning, stroom en magnetische flux

Michael Faraday ontdekte de wiskundige relatie tussen magnetische flux (Φ) en geïnduceerde spanning met deze vergelijking:

De momentane spanning (spanning die op elk moment in de tijd valt) over een draadspoel is gelijk aan het aantal windingen van die spoel rond de kern (N) vermenigvuldigd met de momentane veranderingssnelheid in magnetische flux (dΦ/dt) met de spoel.

In de grafiek (figuur hieronder) wordt dit weergegeven als een reeks sinusgolven (uitgaande van een sinusvormige spanningsbron), waarbij de fluxgolf 90° achterblijft bij de spanningsgolf:

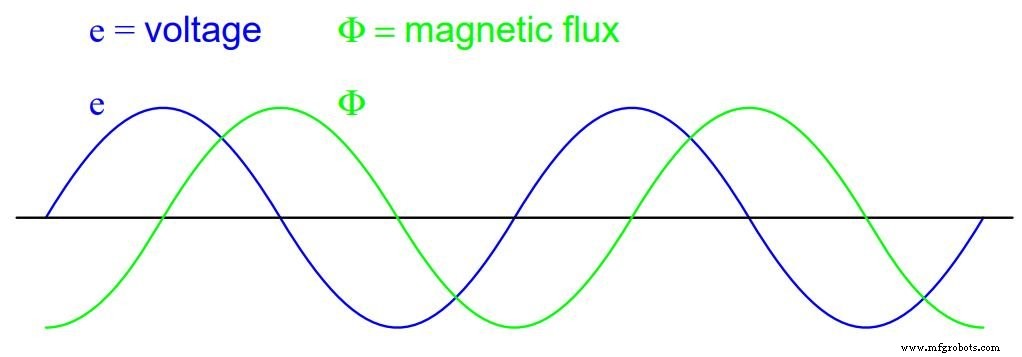
Magnetische flux, net als stroom, loopt 90° achter op de aangelegde spanning

Dit is de reden waarom wisselstroom door een inductor 90 ° achterloopt op de aangelegde spanningsgolfvorm:omdat dat is wat nodig is om een ​​veranderende magnetische flux te produceren waarvan de veranderingssnelheid een tegengestelde spanning produceert in fase met de aangelegde spanning.

Vanwege zijn functie bij het leveren van een magnetiserende kracht (mmf) voor de kern, wordt deze stroom soms de magnetiserende stroom genoemd. .

Er moet worden vermeld dat de stroom door een inductor met ijzeren kern niet perfect sinusvormig is (sinusvormig), vanwege de niet-lineaire B/H-magnetisatiecurve van ijzer.

Als de spoel goedkoop is gebouwd en zo min mogelijk ijzer gebruikt, kan de magnetische fluxdichtheid een hoog niveau bereiken (verzadiging naderen), wat resulteert in een magnetiserende stroomgolfvorm die er ongeveer zo uitziet als de onderstaande afbeelding:

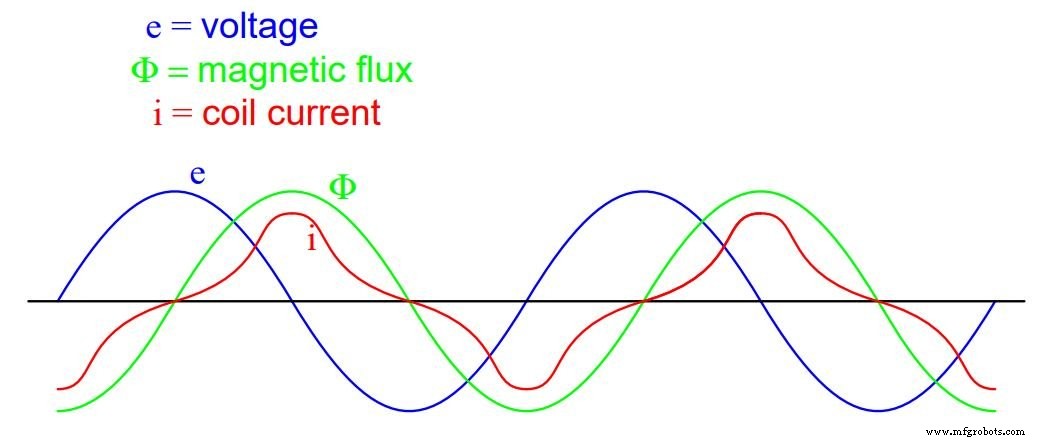
Als de fluxdichtheid de verzadiging nadert, wordt de magnetiserende stroomgolfvorm vervormd

Wanneer een ferromagnetisch materiaal de magnetische fluxverzadiging nadert, zijn onevenredig grotere niveaus van magnetische veldkracht (mmf) vereist om een ​​gelijke toename van de magnetische veldflux (Φ) te leveren.

Omdat mmf evenredig is met de stroom door de magnetiserende spoel (mmf =NI, waarbij "N" het aantal windingen van de draad in de spoel is en "I" de stroom erdoorheen), is de grote toename van mmf die nodig is om de benodigde toename van de flux resulteert in een grote toename van de spoelstroom.

De spoelstroom neemt dus dramatisch toe bij de pieken om een ​​fluxgolfvorm te behouden die niet wordt vervormd, rekening houdend met de klokvormige halve cycli van de huidige golfvorm in de bovenstaande grafiek.

Spannende stroom en zijn effecten

De situatie wordt verder gecompliceerd door energieverliezen binnen de ijzeren kern. De effecten van hysterese en wervelstromen werken samen om de huidige golfvorm verder te vervormen en te compliceren, waardoor deze nog minder sinusvormig wordt en de fase verandert om iets minder dan 90° achter te blijven bij de aangelegde spanningsgolfvorm.

Deze spoelstroom die het resultaat is van de som van alle magnetische effecten in de kern (dΦ/dt-magnetisatie plus hystereseverliezen, wervelstroomverliezen, enz.) wordt de opwindende stroom genoemd. .

De vervorming van de opwindende stroom van een ijzeren kerninductor kan worden geminimaliseerd als deze is ontworpen voor en wordt gebruikt bij zeer lage fluxdichtheden. Over het algemeen vereist dit een kern met een groot dwarsdoorsnede-oppervlak, wat de inductor vaak omvangrijk en duur maakt.

Omwille van de eenvoud gaan we er echter van uit dat onze voorbeeldkern verre van verzadiging is en vrij van alle verliezen, wat resulteert in een perfect sinusoïdale opwindende stroom.

Zoals we al hebben gezien in het hoofdstuk inductoren, creëert het hebben van een stroomgolfvorm die 90° uit fase is met de spanningsgolfvorm een ​​toestand waarin stroom afwisselend wordt geabsorbeerd en teruggevoerd naar het circuit door de inductor.

Als de spoel perfect is (geen draadweerstand, geen magnetische kernverliezen, enz.), zal hij nul vermogen dissiperen.

Laten we nu hetzelfde inductorapparaat beschouwen, behalve deze keer met een tweede spoel (figuur hieronder) die om dezelfde ijzeren kern is gewikkeld. De eerste spoel krijgt het label primaire spoel, terwijl de tweede wordt aangeduid als de secundaire :

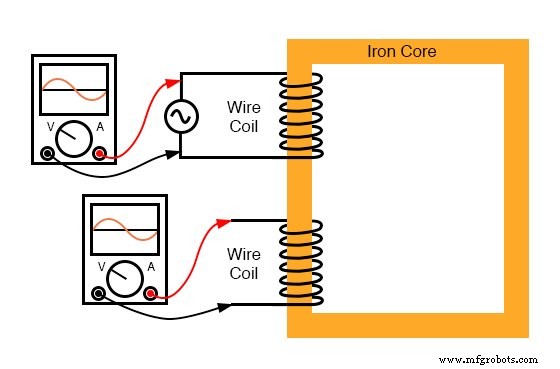
Ferromagnetische kern met primaire spoel (AC-aangedreven) en secundaire spoel.

Wederzijdse inductie

Als deze secundaire spoel dezelfde magnetische fluxverandering ervaart als de primaire (wat zou moeten, uitgaande van een perfecte beheersing van de magnetische flux door de gemeenschappelijke kern), en hetzelfde aantal windingen rond de kern heeft, een spanning van gelijke grootte en fase naar de aangelegde spanning wordt over de lengte geïnduceerd.

In de volgende grafiek (figuur hieronder) is de golfvorm van de geïnduceerde spanning iets kleiner getekend dan de golfvorm van de bronspanning, simpelweg om de een van de ander te onderscheiden:

Secundair met een open circuit ziet dezelfde flux Φ als de primaire. Daarom geïnduceerde secundaire spanning e_s is dezelfde grootte en fase als de primaire spanning e_p .

Dit effect wordt wederzijdse inductie genoemd :de inductie van een spanning in de ene spoel als reactie op een stroomverandering in de andere spoel. Net als normale (zelf)inductie, wordt het gemeten in de eenheid van henries, maar in tegenstelling tot normale inductantie, wordt het gesymboliseerd door de hoofdletter "M" in plaats van de letter "L":

Er zal geen stroom in de secundaire spoel zijn omdat deze een open circuit heeft. Als we er echter een belastingsweerstand op aansluiten, gaat er een wisselstroom door de spoel, in fase met de geïnduceerde spanning (omdat de spanning over een weerstand en de stroom erdoor altijd zijn in fase met elkaar). (Figuur hieronder)

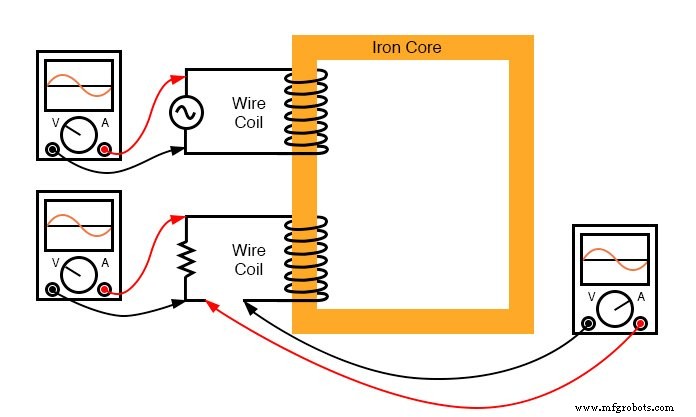
Ohmse belasting op secundair heeft spanning en stroom in fase.

In eerste instantie zou je verwachten dat deze secundaire spoelstroom een ​​extra magnetische flux in de kern veroorzaakt. In feite niet. Als er meer flux in de kern zou worden geïnduceerd, zou er meer spanning in de primaire spoel worden geïnduceerd (onthoud dat e =dΦ/dt).

Dit kan niet gebeuren, omdat de geïnduceerde spanning van de primaire spoel op dezelfde grootte en fase moet blijven om in evenwicht te zijn met de aangelegde spanning, in overeenstemming met de spanningswet van Kirchhoff. Bijgevolg kan de magnetische flux in de kern niet worden beïnvloed door de secundaire spoelstroom.

Maar wat doet verandering is de hoeveelheid mmf in het magnetische circuit.

Magnetomotorische kracht

Magnetomotorische kracht wordt geproduceerd wanneer er stroom door een draad vloeit. Gewoonlijk gaat deze mmf gepaard met magnetische flux, in overeenstemming met de mmf=ΦR "magnetische wet van Ohm" -vergelijking.

In dit geval is extra flux echter niet toegestaan, dus de enige manier waarop de mmf van de secundaire spoel kan bestaan, is als een tegenwerkende mmf wordt gegenereerd door de primaire spoel, van gelijke grootte en tegenfase.

Dit is inderdaad wat er gebeurt:er vormt zich een wisselstroom in de primaire spoel - 180° uit fase met de stroom van de secundaire spoel - om deze tegenwerkende mmf te genereren en extra kernflux te voorkomen.

Polariteitsmarkeringen en stroomrichtingpijlen zijn aan de afbeelding toegevoegd om de faserelaties te verduidelijken:(Figuur hieronder)

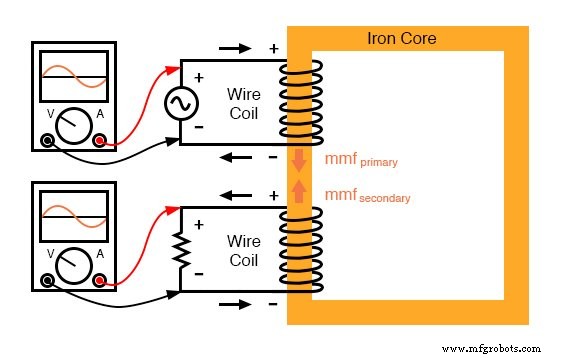
Flux blijft constant bij het uitoefenen van een belasting. Er wordt echter een tegenwerkende mmf geproduceerd door de geladen secundaire.

Als u dit proces een beetje verwarrend vindt, hoeft u zich geen zorgen te maken. Transformatordynamica is een complex onderwerp. Wat belangrijk is om te begrijpen, is dit:wanneer een wisselspanning wordt toegepast op de primaire spoel, creëert deze een magnetische flux in de kern, die een wisselspanning in de secundaire spoel induceert die in fase is met de bronspanning.

Elke stroom die door de secundaire spoel wordt getrokken om een ​​belasting van stroom te voorzien, induceert een overeenkomstige stroom in de primaire spoel, waarbij stroom wordt onttrokken aan de bron.

Wederzijdse inductie en transformatoren

Merk op hoe de primaire spoel zich gedraagt ​​als een belasting ten opzichte van de wisselspanningsbron en hoe de secundaire spoel zich gedraagt ​​als een bron ten opzichte van de weerstand.

In plaats van dat energie afwisselend wordt geabsorbeerd en teruggevoerd naar het primaire spoelcircuit, wordt energie nu gekoppeld naar de secundaire spoel waar het wordt geleverd aan een dissipatieve (energieverbruikende) belasting. Voor zover de bron "weet", voedt het rechtstreeks de weerstand.

Natuurlijk is er ook een extra primaire spoelstroom die 90° achterblijft bij de aangelegde spanning, net genoeg om de kern te magnetiseren om de nodige spanning te creëren voor het balanceren met de bron (de opwindende stroom ).

We noemen dit type apparaat een transformator , omdat het elektrische energie omzet in magnetische energie en vervolgens weer terug in elektrische energie. Omdat de werking ervan afhankelijk is van elektromagnetische inductie tussen twee stationaire spoelen en een magnetische flux van veranderende grootte en "polariteit", zijn transformatoren noodzakelijkerwijs AC-apparaten.

Het schematische symbool ziet eruit als twee inductoren (spoelen) die dezelfde magnetische kern delen:(figuur hieronder)

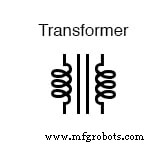
Het schematische symbool voor een transformator bestaat uit twee inductorsymbolen, gescheiden door lijnen die een ferromagnetische kern aangeven.

De twee inductorspoelen zijn gemakkelijk te onderscheiden in het bovenstaande symbool. Het paar verticale lijnen vertegenwoordigen een ijzeren kern die beide inductoren gemeen hebben. Hoewel veel transformatoren ferromagnetische kernmaterialen hebben, zijn er enkele die dat niet hebben, omdat hun samenstellende inductoren magnetisch met elkaar verbonden zijn door de lucht.

De volgende foto toont een vermogenstransformator van het type dat wordt gebruikt in gasontladingsverlichting. Hier zijn duidelijk de twee inductorspoelen te zien, gewikkeld rond een ijzeren kern. Hoewel de meeste transformatorontwerpen de spoelen en de kern ter bescherming in een metalen frame omsluiten, is deze specifieke transformator open om te bekijken en dient dus zijn illustratieve doel goed (figuur hieronder):

Voorbeeld van een gasontladingsverlichtingstransformator.

Primaire en secundaire wikkelingen

Beide draadspiralen zijn hier te zien met koperkleurige lakisolatie. De bovenste spoel is groter dan de onderste spoel en heeft een groter aantal "windingen" rond de kern. In transformatoren worden de inductorspoelen vaak wikkelingen genoemd , verwijzend naar het fabricageproces waarbij de draad wordt opgewikkeld rond het kernmateriaal.

Zoals gemodelleerd in ons eerste voorbeeld, wordt de aangedreven inductor van een transformator de primaire . genoemd wikkeling, terwijl de niet-aangedreven spoel de secundaire . wordt genoemd kronkelend.

Op de volgende foto (figuur hieronder) wordt een transformator getoond die doormidden is gesneden, waardoor de dwarsdoorsnede van de ijzeren kern en beide wikkelingen zichtbaar zijn. Net als de eerder getoonde transformator, gebruikt deze unit ook primaire en secundaire wikkelingen met verschillende windingen.

De draaddikte kan ook verschillen tussen primaire en secundaire wikkelingen. De reden voor dit verschil in draaddikte zal duidelijk worden in de volgende sectie van dit hoofdstuk.

Bovendien is te zien dat de ijzeren kern op deze foto is gemaakt van veel dunne platen (laminaten) in plaats van een massief stuk. De reden hiervoor zal ook in een later deel van dit hoofdstuk worden uitgelegd.

De doorsnede van de transformator toont de kern en de windingen.

Eenvoudige transformatoractie met SPICE

Het is gemakkelijk om eenvoudige transformatoractie te demonstreren met SPICE, waarbij de primaire en secundaire wikkelingen van de gesimuleerde transformator worden ingesteld als een paar "wederzijdse" inductoren (figuur hieronder).

De coëfficiënt van magnetische veldkoppeling wordt gegeven aan het einde van de "k" -lijn in de SPICE-circuitbeschrijving, waarbij dit voorbeeld bijna perfect is ingesteld (1.000). Deze coëfficiënt beschrijft hoe nauw "verbonden" de twee inductoren magnetisch zijn. Hoe beter deze twee inductoren magnetisch zijn gekoppeld, hoe efficiënter de energieoverdracht tussen hen zou moeten zijn.

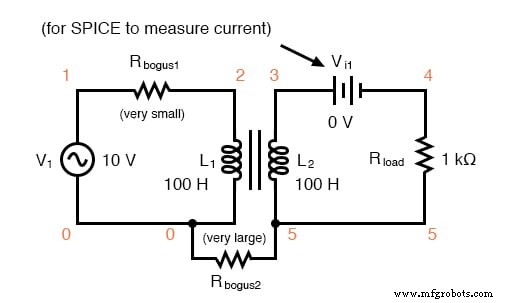
Kruidencircuit voor gekoppelde inductoren.

transformator v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 ** Deze regel vertelt SPICE dat de twee inductoren ** l1 en l2 zijn magnetisch aan elkaar "verbonden" k l1 l2 0.999 vi1 3 4 ac 0 rbelasting 4 5 1k .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .einde 

Opmerking:de R_nep weerstanden zijn vereist om aan bepaalde eigenaardigheden van SPICE te voldoen. De eerste verbreekt de anders continue lus tussen de spanningsbron en L₁ wat door SPICE niet zou zijn toegestaan. De tweede biedt een pad naar aarde (knooppunt 0) vanaf het secundaire circuit, nodig omdat SPICE niet kan werken met niet-geaarde circuits.

freq v(2) i(v1) 6.000E+01 1.000E+01 9.975E-03 Primaire wikkeling freq v(3,5) i(vi1) 6.000E+01 9.962E+00 9.962E-03 Secundaire wikkeling 

Merk op dat met gelijke inductanties voor beide wikkelingen (elk 100 henries), de wisselspanningen en -stromen bijna gelijk zijn voor de twee. Het verschil tussen primaire en secundaire stromen is de eerder genoemde magnetiserende stroom:de 90 ° naijlstroom die nodig is om de kern te magnetiseren.

Zoals hier te zien is, is deze meestal erg klein in vergelijking met de primaire stroom die wordt geïnduceerd door de belasting, en dus zijn de primaire en secundaire stromen bijna gelijk. Wat u hier ziet, is vrij typerend voor de efficiëntie van transformatoren.

Alles onder de 95% efficiëntie wordt als slecht beschouwd voor moderne transformatorontwerpen, en deze overdracht van vermogen vindt plaats zonder bewegende delen of andere componenten die onderhevig zijn aan slijtage.

Als we de belastingsweerstand verlagen om meer stroom te trekken met dezelfde hoeveelheid spanning, zien we dat de stroom door de primaire wikkeling als reactie toeneemt.

Hoewel de wisselstroombron niet rechtstreeks is aangesloten op de belastingsweerstand (in plaats daarvan is hij elektromagnetisch "gekoppeld"), zal de hoeveelheid stroom die uit de bron wordt getrokken bijna hetzelfde zijn als de hoeveelheid stroom die zou worden getrokken als de belasting was rechtstreeks verbonden met de bron.

Kijk eens goed naar de volgende twee SPICE-simulaties, die laten zien wat er gebeurt met verschillende waarden van belastingsweerstanden:

transformator v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 ** Let op de belastingsweerstandswaarde van 200 ohm rbelasting 4 5 200 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .einde 

freq v(2) i(v1) 6.000E+01 1.000E+01 4.679E-02 freq v(3,5) i(vi1) 6.000E+01 9.348E+00 4.674E-02 

Merk op hoe de primaire stroom de secundaire stroom nauw volgt. In onze eerste simulatie waren beide stromen ongeveer 10 mA, maar nu zijn ze beide ongeveer 47 mA. In deze tweede simulatie zijn de twee stromen dichter bij gelijkheid, omdat de magnetiserende stroom hetzelfde blijft als voorheen terwijl de belastingsstroom is toegenomen.

Merk ook op hoe de secundaire spanning wat is afgenomen met de zwaardere (grotere stroom) belasting. Laten we een andere simulatie proberen met een nog lagere waarde van belastingsweerstand (15 Ω):

transformator v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 rbelasting 4 5 15 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .einde 

freq v(2) i(v1) 6.000E+01 1.000E+01 1.301E-01 freq v(3,5) i(vi1) 6.000E+01 1.950E+00 1.300E-01 

Onze belastingsstroom is nu 0,13 ampère of 130 mA, wat aanzienlijk hoger is dan de vorige keer. De primaire stroom is bijna hetzelfde, maar merk op hoe de secundaire spanning ver onder de primaire spanning is gedaald (1,95 volt versus 10 volt bij de primaire).

De reden hiervoor is een onvolkomenheid in ons transformatorontwerp:omdat de primaire en secundaire inductanties niet perfect zijn gekoppeld (een k-factor van 0.999 ipv 1.000) er is “verdwaald” of “lekkage inductie. Met andere woorden, een deel van het magnetische veld is niet verbonden met de secundaire spoel en kan er dus geen energie aan koppelen:(figuur hieronder)

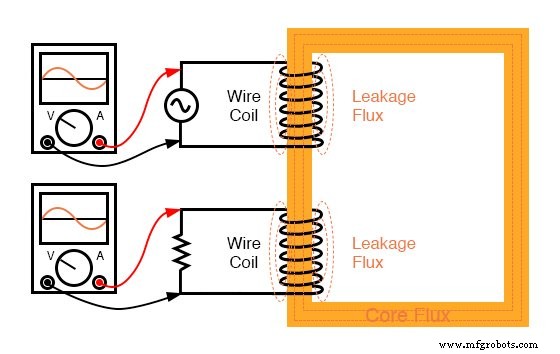
Lekkage-inductantie wordt veroorzaakt doordat magnetische flux niet beide wikkelingen doorsnijdt.

Bijgevolg slaat deze "lekkage" -flux alleen energie op en geeft deze terug aan het broncircuit via zelfinductie, en werkt effectief als een serie-impedantie in zowel primaire als secundaire circuits. De spanning daalt over deze serie-impedantie, wat resulteert in een lagere belastingsspanning:de spanning over de belasting "zakt" naarmate de belastingsstroom toeneemt. (Figuur hieronder)

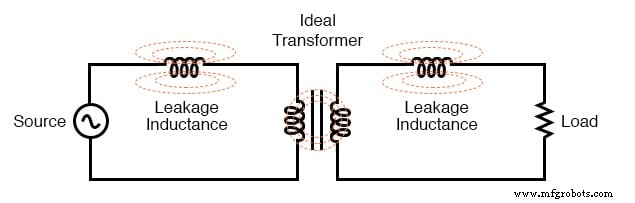
Equivalent circuit modelleert lekinductantie als serie-inductoren onafhankelijk van de "ideale transformator".

Als we het ontwerp van de transformator veranderen voor een betere magnetische koppeling tussen de primaire en secundaire spoelen, zullen de cijfers voor de spanning tussen de primaire en secundaire wikkelingen weer veel dichter bij gelijkheid zijn:

transformator v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 ** Koppelingsfactor =0,99999 in plaats van 0,999 k l1 l2 0,99999 vi1 3 4 ac 0 rbelasting 4 5 15 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .einde 

freq v(2) i(v1) 6.000E+01 1.000E+01 6.658E-01 freq v(3,5) i(vi1) 6.000E+01 9.987E+00 6.658E-01 

Hier zien we dat onze secundaire spanning weer gelijk is aan de primaire en dat de secundaire stroom ook gelijk is aan de primaire stroom. Helaas is het bouwen van een echte transformator met koppeling deze compleet erg moeilijk.

Een compromisoplossing is om zowel primaire als secundaire spoelen met minder inductantie te ontwerpen, waarbij de strategie is dat minder inductantie in het algemeen leidt tot minder "lekkage"-inductantie om problemen te veroorzaken, voor een bepaalde mate van inefficiëntie van de magnetische koppeling. Dit resulteert in een belastingsspanning die dichter bij ideaal is met dezelfde (hoge stroom zware) belasting en dezelfde koppelingsfactor:

transformator v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 ** inductie =1 henry in plaats van 100 henry l1 2 0 1 l2 3 5 1 k l1 l2 0.999 vi1 3 4 ac 0 rbelasting 4 5 15 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .einde 

freq v(2) i(v1) 6.000E+01 1.000E+01 6.664E-01 freq v(3,5) i(vi1) 6.000E+01 9.977E+00 6.652E-01 

Door simpelweg primaire en secundaire spoelen met minder inductantie te gebruiken, is de belastingsspanning voor deze zware belasting (hoge stroom) teruggebracht tot bijna ideale niveaus (9,977 volt). Op dit punt zou je je kunnen afvragen:"Als minder inductantie alles is wat nodig is om bijna ideale prestaties te bereiken onder zware belasting, waarom zou je je dan zorgen maken over de efficiëntie van de koppeling?

Als het onmogelijk is om een ​​transformator met een perfecte koppeling te bouwen, maar eenvoudig om spoelen met een lage inductantie te ontwerpen, waarom dan niet gewoon alle transformatoren bouwen met spoelen met een lage inductantie en een uitstekende efficiëntie hebben, zelfs met een slechte magnetische koppeling?”

Het antwoord op deze vraag is te vinden in een andere simulatie:dezelfde laag-inductantie transformator, maar deze keer met een lichtere belasting (minder stroom) van 1 kΩ in plaats van 15 Ω:

transformator v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 1 l2 3 5 1 k l1 l2 0.999 vi1 3 4 ac 0 rbelasting 4 5 1k .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .einde 

freq v(2) i(v1) 6.000E+01 1.000E+01 2.835E-02 freq v(3,5) i(vi1) 6.000E+01 9.990E+00 9.990E-03 

Met lagere wikkelinductanties zijn de primaire en secundaire spanningen dichter bij gelijk, maar de primaire en secundaire stromen niet. In dit specifieke geval is de primaire stroom 28,35 mA, terwijl de secundaire stroom slechts 9,990 mA is:bijna drie keer zoveel stroom in de primaire als de secundaire.

Waarom is dit? Met minder inductantie in de primaire wikkeling, is er minder inductieve reactantie en bijgevolg een veel grotere magnetiserende stroom. Een aanzienlijk deel van de stroom door de primaire wikkeling werkt alleen om de kern te magnetiseren in plaats van overdracht nuttige energie naar de secundaire wikkeling en belasting.

Een ideale transformator met identieke primaire en secundaire wikkelingen zou voor elke belastingstoestand een gelijke spanning en stroom in beide sets wikkelingen vertonen. In een perfecte wereld zouden transformatoren elektrisch vermogen net zo soepel van primair naar secundair overdragen alsof de belasting rechtstreeks op de primaire stroombron was aangesloten, zonder dat daar een transformator aanwezig was.

U kunt echter zien dat dit ideale doel alleen kan worden bereikt als er een perfecte . is koppeling van magnetische flux tussen primaire en secundaire wikkelingen. Omdat dit onmogelijk te bereiken is, moeten transformatoren worden ontworpen om te werken binnen bepaalde verwachte spannings- en belastingenbereiken om zo ideaal mogelijk te presteren.

Vooralsnog is het belangrijkste om in gedachten te houden het basisprincipe van een transformator:de overdracht van vermogen van het primaire naar het secundaire circuit via elektromagnetische koppeling.

BEOORDELING:

• Wederzijdse inductie is waar de magnetische flux van twee of meer inductoren "verbonden" zijn, zodat de spanning in één spoel wordt geïnduceerd die evenredig is met de veranderingssnelheid van de stroom in een andere.
• Een transformator is een apparaat gemaakt van twee of meer inductoren, waarvan er één wordt gevoed door wisselstroom, waardoor een wisselspanning over de tweede inductor wordt opgewekt. Als de tweede inductor is aangesloten op een belasting, wordt de stroom elektromagnetisch gekoppeld van de stroombron van de eerste inductor naar die belasting.
• De aangedreven spoel in een transformator wordt de primaire wikkeling genoemd . De niet-aangedreven spoel in een transformator wordt de secundaire wikkeling genoemd .
• De magnetische flux in de kern (Φ) blijft 90° achter op de golfvorm van de bronspanning. De stroom die door de primaire spoel van de bron wordt getrokken om deze flux te produceren, wordt de magnetiserende stroom genoemd. , en het blijft ook 90° achter op de voedingsspanning.
• De totale primaire stroom in een onbelaste transformator wordt de opwindende stroom genoemd en bestaat uit magnetiserende stroom plus eventuele extra stroom die nodig is om kernverliezen te overwinnen. Het is nooit perfect sinusvormig in een echte transformator, maar kan meer worden gemaakt als de transformator zo is ontworpen en gebruikt dat de magnetische fluxdichtheid tot een minimum wordt beperkt.
• Kernflux induceert een spanning in elke spoel die om de kern is gewikkeld. De geïnduceerde spanning(en) zijn idealiter in fase met de spanning van de primaire wikkeling en delen dezelfde golfvorm.
• Elke stroom die door een belasting door de secundaire wikkeling wordt getrokken, wordt "gereflecteerd" naar de primaire wikkeling en getrokken uit de spanningsbron alsof de bron rechtstreeks een vergelijkbare belasting voedt.

GERELATEERDE WERKBLAD:

• Wederzijdse inductie werkblad
• Werkblad Step-up, Step-down en isolatietransformatoren