Serie weerstand-inductorcircuits

In de vorige sectie hebben we onderzocht wat er zou gebeuren in eenvoudige AC-circuits met alleen weerstand en alleen inductor. Nu gaan we de twee componenten in serie met elkaar mengen en de effecten onderzoeken.

Serieweerstand Inductor Circuit Voorbeeld

Neem dit circuit als voorbeeld om mee te werken:

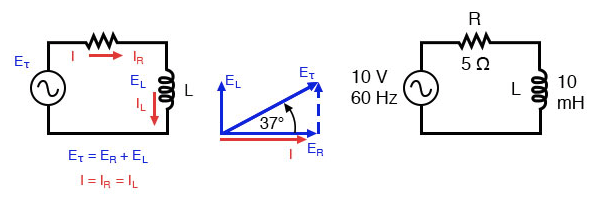
Inductorcircuit met serieweerstand:stroom blijft 0o tot 90o achter bij aangelegde spanning.

De weerstand biedt 5 Ω weerstand tegen wisselstroom, ongeacht de frequentie, terwijl de inductor een reactantie van 3,7699 Ω biedt tegen wisselstroom bij 60 Hz.

Omdat de weerstand van de weerstand een reëel getal is (5 ∠ 0°, of 5 + j0 ), en de reactantie van de inductor een denkbeeldig getal is (3.7699 Ω ∠ 90°, of 0 + j3.7699 Ω), is het gecombineerde effect van de twee componenten zullen een oppositie tegen stroom zijn die gelijk is aan de complexe som van de twee getallen.

Deze gecombineerde oppositie zal een vectorcombinatie zijn van weerstand en reactantie. Om deze oppositie bondig uit te drukken, hebben we een meer omvattende term nodig voor oppositie tegen stroom dan alleen weerstand of reactantie.

Deze term heet impedantie , het symbool is Z, en het wordt ook uitgedrukt in de eenheid van ohm, net als weerstand en reactantie. In het bovenstaande voorbeeld is de totale circuitimpedantie:

Weerstand in de wet van Ohm

Impedantie is gerelateerd aan spanning en stroom, net zoals je zou verwachten, op een manier die vergelijkbaar is met weerstand in de wet van Ohm:

In feite is dit een veel uitgebreidere vorm van de wet van Ohm dan wat werd geleerd in DC-elektronica (E =IR), net zoals impedantie een veel uitgebreidere uitdrukking is van oppositie tegen de stroomstroom dan weerstand. Elke weerstand en elke reactantie, afzonderlijk of in combinatie (serie/parallel), kan en moet worden weergegeven als een enkele impedantie in een AC-circuit.

Om de stroom in het bovenstaande circuit te berekenen, moeten we eerst een fasehoekreferentie geven voor de spanningsbron, waarvan algemeen wordt aangenomen dat deze nul is. (De fasehoeken van resistieve en inductieve impedantie zijn altijd respectievelijk 0° en +90°, ongeacht de gegeven fasehoeken voor spanning of stroom).

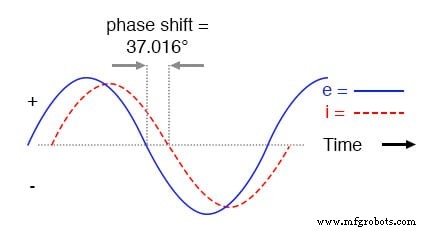
Net als bij de puur inductieve schakeling blijft de stroomgolf achter op de spanningsgolf (van de bron), hoewel de lag deze keer niet zo groot is:slechts 37.016° in tegenstelling tot een volledige 90° zoals het geval was in de puur inductieve schakeling .

Stroom blijft achter bij spanning in een serie L-R-circuit.

Voor de weerstand en de inductor zijn de faserelaties tussen spanning en stroom niet veranderd. De spanning over de weerstand is in fase (0° verschuiving) met de stroom erdoorheen, en de spanning over de inductor is +90° uit fase met de stroom die er doorheen gaat. We kunnen dit wiskundig verifiëren:

De spanning over de weerstand heeft exact dezelfde fasehoek als de stroom erdoorheen, wat ons vertelt dat E en ik in fase zijn (alleen voor de weerstand).

De spanning over de spoel heeft een fasehoek van 52,984°, terwijl de stroom door de spoel een fasehoek heeft van -37,016°, een verschil van precies 90° tussen beide. Dit vertelt ons dat E en I nog steeds 90° uit fase zijn (alleen voor de spoel).

Gebruik de spanningswet van Kirchhoff

We kunnen ook wiskundig bewijzen dat deze complexe waarden bij elkaar optellen om de totale spanning te maken, net zoals de spanningswet van Kirchhoff zou voorspellen:

Berekenen met SPICE

Laten we de geldigheid van onze berekeningen controleren met SPICE:

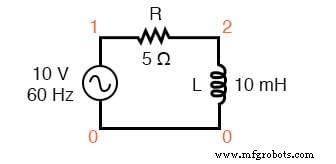
Kruidencircuit:R-L.

v1 1 0 ac 10 sin r1 1 2 5 l1 2 0 10m .ac lin 1 60 60 .print ac v(1,2) v(2,0) i(v1) .print ac vp(1,2) vp(2,0) ip(v1) .einde 

freq v(1,2) v(2) i(v1) 6.000E+01 7.985E+00 6.020E+00 1.597E+00 freq vp(1,2) vp(2) ip(v1) 6.000E+01 -3.702E+01 5.298E+01 1.430E+0 

Merk op dat SPICE, net als bij DC-circuits, huidige cijfers uitvoert alsof ze negatief zijn (180 ° uit fase) met de voedingsspanning. In plaats van een fasehoek van -37,016° krijgen we een huidige fasehoek van 143°(-37° + 180°).

Dit is slechts een eigenaardigheid van SPICE en vertegenwoordigt niets significants in de circuitsimulatie zelf. Merk op hoe zowel de fase-aflezingen van de weerstand als de inductor overeenkomen met onze berekeningen (respectievelijk -37,02° en 52,98°), precies zoals we hadden verwacht.

Met al deze cijfers om bij te houden voor zelfs zo'n eenvoudig circuit als dit, zou het voor ons gunstig zijn om de "tabel" -methode te gebruiken. Het toepassen van een tabel op dit eenvoudige serieweerstand-inductorcircuit zou als zodanig verlopen.

Maak eerst een tabel voor E/I/Z-cijfers en vul alle componentwaarden in deze termen in (met andere woorden, voeg geen werkelijke weerstands- of inductantiewaarden in respectievelijk ohm en henries in de tabel in; converteer ze liever in complexe impedantiecijfers en schrijf die op in):

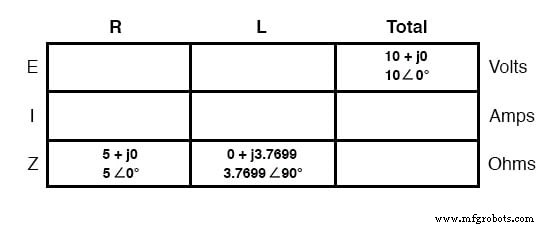
Hoewel het niet nodig is, vind ik het nuttig om beide . te schrijven de rechthoekige en polaire vormen van elke hoeveelheid in de tabel. Als u een rekenmachine gebruikt die complexe berekeningen kan uitvoeren zonder de noodzaak van conversie tussen rechthoekige en polaire vormen, dan is deze extra documentatie volledig overbodig.

Als je echter gedwongen wordt om complexe rekenkundige "handmatige" berekeningen uit te voeren (optellen en aftrekken in rechthoekige vorm, en vermenigvuldigen en delen in polaire vorm), zal het inderdaad nuttig zijn om elke hoeveelheid in beide vormen te schrijven.

Nu onze "gegeven" cijfers op hun respectievelijke locaties in de tabel zijn ingevoegd, kunnen we net als bij DC te werk gaan:bepaal de totale impedantie uit de individuele impedanties. Aangezien dit een serieschakeling is, weten we dat oppositie tegen stroom (weerstand of impedantie) wordt toegevoegd om de totale oppositie te vormen:

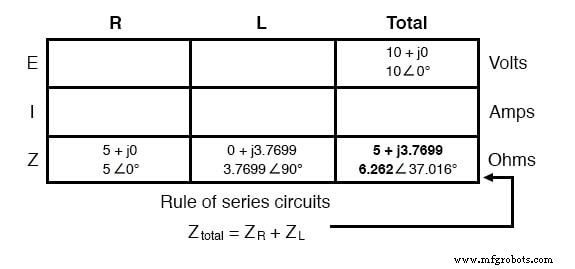
Nu we de totale spanning en totale impedantie kennen, kunnen we de wet van Ohm (I=E/Z) toepassen om de totale stroom te bepalen:

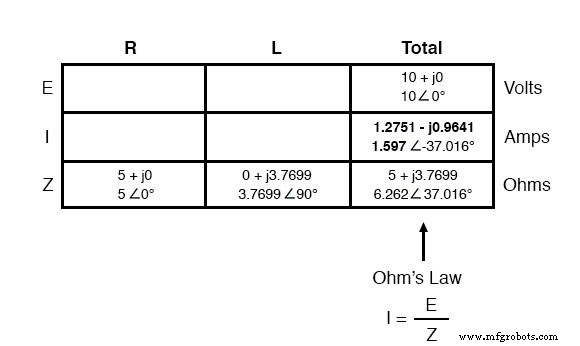
Net als bij DC wordt de totale stroom in een serie AC-circuit gelijkelijk gedeeld door alle componenten. Dit is nog steeds waar, omdat er in een serieschakeling slechts één pad is om de stroom te laten stromen, daarom moet de snelheid van hun stroom overal uniform zijn. Bijgevolg kunnen we de cijfers voor stroom overbrengen naar de kolommen voor zowel de weerstand als de inductor:

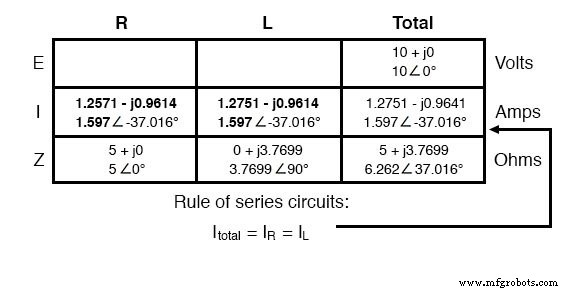
Nu hoeft alleen nog de spanningsval over de weerstand en de inductor te worden berekend. Dit wordt gedaan door het gebruik van de wet van Ohm (E=IZ), verticaal toegepast in elke kolom van de tabel:

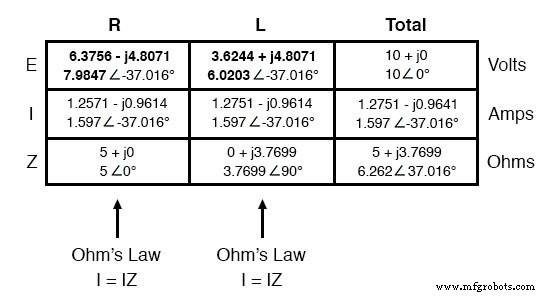
En daarmee is onze tafel compleet. Exact dezelfde regels die we hebben toegepast bij de analyse van DC-circuits zijn ook van toepassing op AC-circuits, met het voorbehoud dat alle hoeveelheden moeten worden weergegeven en berekend in complexe in plaats van scalaire vorm.

Zolang faseverschuiving correct wordt weergegeven in onze berekeningen, is er geen fundamenteel verschil in de manier waarop we de basisanalyse van AC-circuits versus DC benaderen.

Dit is een goed moment om de relatie tussen deze berekende cijfers en de metingen die zijn gegeven door feitelijke instrumentmetingen van spanning en stroom te bekijken.

De cijfers hier die direct betrekking hebben op real-life metingen zijn die in polaire notatie , niet rechthoekig! Met andere woorden, als u een voltmeter over de weerstand in dit circuit zou aansluiten, zou dit 7.9847 aangeven volt, niet 6.3756 (echt rechthoekig) of 4.8071 (denkbeeldig rechthoekig) volt.

Om dit grafisch te beschrijven, vertellen meetinstrumenten u eenvoudig hoe lang de vector is voor die bepaalde grootheid (spanning of stroom).

Rechthoekige notatie, hoewel handig voor rekenkundig optellen en aftrekken, is een meer abstracte vorm van notatie dan polair in relatie tot metingen in de echte wereld. Zoals ik eerder al zei, zal ik zowel polaire als rechthoekige vormen van elke hoeveelheid in mijn AC-circuittabellen aangeven, gewoon voor het gemak van wiskundige berekeningen.

Dit is niet absoluut noodzakelijk, maar kan handig zijn voor degenen die het volgen zonder het voordeel van een geavanceerde rekenmachine. Als we ons zouden beperken tot het gebruik van slechts één vorm van notatie, zou de beste keuze polair zijn, omdat dit de enige is die direct kan worden gecorreleerd aan echte metingen.

Impedantie (Z) van een serie R-L-schakeling kan worden berekend, gegeven de weerstand (R) en de inductieve reactantie (XL). Aangezien E =IR, E =IXL en E =IZ, zijn weerstand, reactantie en impedantie respectievelijk evenredig met de spanning. Het spanningsfasediagram kan dus worden vervangen door een soortgelijk impedantiediagram.

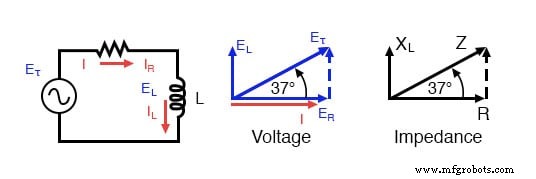
Serie:R-L circuit Impedantie fasordiagram.

Voorbeeld: Gegeven:een weerstand van 40 in serie met een spoel van 79,58 millihenry. Zoek de impedantie bij 60 hertz.

 XL =2πfL XL =2π·60·79.58×10-3 XL =30 Z =R + jXL Z =40 + j30 |Z| =sqrt(402 + 302) =50 Ω ∠Z =boogtangens (30/40) =36,87° Z =40 + j30 =50∠36,87° 

BEOORDELING:

• Impedantie is de totale maat van weerstand tegen elektrische stroom en is de complexe (vector) som van ("echte") weerstand en ("denkbeeldige") reactantie. Het wordt gesymboliseerd door de letter "Z" en gemeten in ohm, net als weerstand (R) en reactantie (X).
• Impedanties (Z) worden op dezelfde manier beheerd als weerstanden (R) in serieschakelingsanalyse:serie-impedanties worden opgeteld om de totale impedantie te vormen. Zorg er wel voor dat u alle berekeningen in complexe (niet scalaire) vorm uitvoert! Z_Totaal =Z₁ + Z₂ + . . . Z_n
• Een puur resistieve impedantie heeft altijd een fasehoek van exact 0° (ZR =R Ω ∠ 0°).
• Een puur inductieve impedantie heeft altijd een fasehoek van exact +90° (ZL =XL Ω ∠ 90°).
• Wet van Ohm voor AC-circuits:E =IZ; ik =E/Z; Z =E/I
• Als weerstanden en inductoren in circuits met elkaar worden gemengd, heeft de totale impedantie een fasehoek ergens tussen 0° en +90°. De circuitstroom heeft een fasehoek ergens tussen 0° en -90°.
• Serie AC-circuits vertonen dezelfde fundamentele eigenschappen als serie DC-circuits:de stroom is uniform door het hele circuit, spanningsdalingen vormen samen de totale spanning en impedanties vormen samen de totale impedantie.

GERELATEERDE WERKBLAD:

• Inductoren werkblad
• Werkblad Weerstand, reactantie en impedantie
• Inductieve reactantie werkblad