Serie weerstand-condensatorcircuits
In het laatste gedeelte hebben we geleerd wat er zou gebeuren in eenvoudige AC-circuits met alleen weerstand en alleen condensator. Nu gaan we de twee componenten in serie samenvoegen en de effecten onderzoeken.
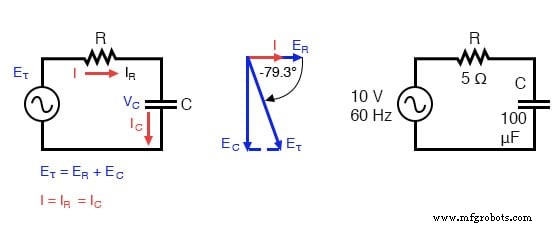
Serie condensatorcircuit:spanning loopt achter op stroom met 0° tot 90°.
Impedantieberekening
De weerstand biedt 5 Ω weerstand tegen wisselstroom, ongeacht de frequentie, terwijl de condensator 26,5258 Ω reactantie biedt tegen wisselstroom bij 60 Hz.
Omdat de weerstand van de weerstand een reëel getal is (5 ∠ 0°, of 5 + j0 ), en de reactantie van de condensator een denkbeeldig getal is (26.5258 Ω ∠ -90°, of 0 - j26.5258 Ω), is het gecombineerde effect van de twee componenten zal een oppositie tegen stroom zijn die gelijk is aan de complexe som van de twee getallen.
De term voor deze complexe oppositie tegen stroom is impedantie , het symbool is Z, en het wordt ook uitgedrukt in de eenheid van ohm, net als weerstand en reactantie. In het bovenstaande voorbeeld is de totale circuitimpedantie:

Impedantie is gerelateerd aan spanning en stroom, net zoals je zou verwachten, op een manier die vergelijkbaar is met weerstand in de wet van Ohm:

In feite is dit een veel uitgebreidere vorm van de wet van Ohm dan wat werd geleerd in DC-elektronica (E =IR), net zoals impedantie een veel uitgebreidere uitdrukking is van oppositie tegen de stroom van elektronen dan eenvoudige weerstand. Elke weerstand en elke reactantie, afzonderlijk of in combinatie (serie/parallel), kan en moet worden weergegeven als een enkele impedantie.
Huidige berekening
Om de stroom in het bovenstaande circuit te berekenen, moeten we eerst een fasehoekreferentie geven voor de spanningsbron, waarvan algemeen wordt aangenomen dat deze nul is. (De fasehoeken van resistieve en capacitieve impedantie zijn altijd respectievelijk 0° en -90°, ongeacht de gegeven fasehoeken voor spanning of stroom.)
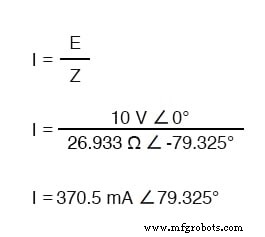
Net als bij het puur capacitieve circuit leidt de stroomgolf de spanningsgolf (van de bron), hoewel dit keer het verschil 79,325° is in plaats van een volledige 90°.
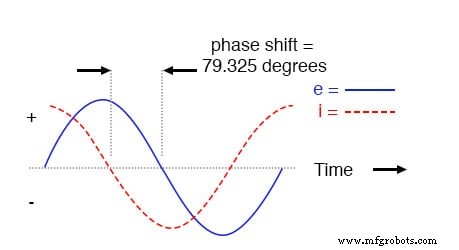
Spanning blijft achter bij stroom (stroomkabelspanning) in een serieel RC-circuit.
Tabelmethode
Zoals we in het hoofdstuk AC-inductantie hebben geleerd, is de "tabel"-methode voor het organiseren van circuithoeveelheden een zeer nuttig hulpmiddel voor AC-analyse, net als voor DC-analyse. Laten we bekende cijfers voor deze serieschakeling in een tabel plaatsen en de analyse voortzetten met behulp van deze tool:
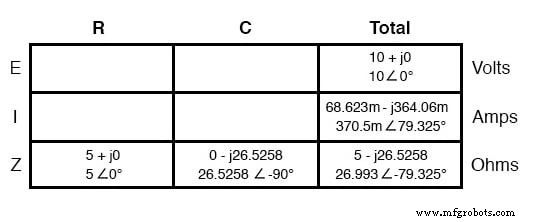
De stroom in een serieschakeling wordt gelijkelijk gedeeld door alle componenten, dus de cijfers in de kolom "Totaal" voor stroom kunnen ook worden verdeeld over alle andere kolommen:
Als we doorgaan met onze analyse, kunnen we de wet van Ohm (E =IR) verticaal toepassen om de spanning over de weerstand en condensator te bepalen:
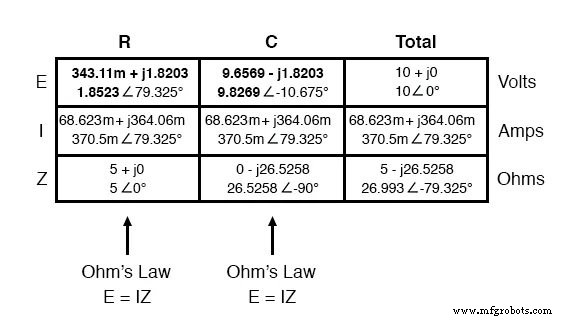
Merk op hoe de spanning over de weerstand exact dezelfde fasehoek heeft als de stroom erdoorheen, wat ons vertelt dat E en ik in fase zijn (alleen voor de weerstand). De spanning over de condensator heeft een fasehoek van -10,675°, precies 90° minder dan de fasehoek van de circuitstroom. Dit vertelt ons dat de spanning en stroom van de condensator nog steeds 90° uit fase zijn met elkaar.
Berekeningen met SPICE
Laten we onze berekeningen eens bekijken met SPICE:
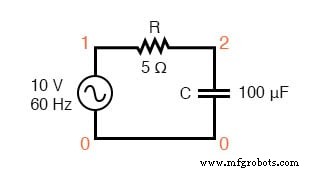
Kruidencircuit:RC.
ac r-c circuit v1 1 0 ac 10 sin r1 1 2 5 c1 2 0 100u .ac lin 1 60 60 .print ac v(1,2) v(2,0) i(v1) .print ac vp(1,2) vp(2,0) ip(v1) .einde freq v(1,2) v(2) i(v1) 6.000E+01 1.852E+00 9.827E+00 3.705E-01 freq vp(1,2) vp(2) ip(v1) 6.000E+01 7.933E+01 -1.067E+01 -1.007E+02

Nogmaals, SPICE drukt de huidige fasehoek verwarrend af met een waarde die gelijk is aan de echte fasehoek plus 180° (of minus 180°).
Het is echter eenvoudig om dit cijfer te corrigeren en te controleren of ons werk correct is. In dit geval komt de output van -100,7° van SPICE voor de huidige fasehoek overeen met een positieve 79,3°, wat overeenkomt met ons eerder berekende cijfer van 79,325°.
Nogmaals, het moet worden benadrukt dat de berekende cijfers die overeenkomen met echte spannings- en stroommetingen die zijn in polaire vorm, geen rechthoekige vorm!
Als we bijvoorbeeld dit serieweerstand-condensatorcircuit zouden bouwen en de spanning over de weerstand zouden meten, zou onze voltmeter 1.8523 aangeven volt, niet 343,11 millivolt (echt rechthoekig) of 1,8203 volt (denkbeeldig rechthoekig).
Echte instrumenten die op echte circuits zijn aangesloten, geven indicaties die overeenkomen met de vectorlengte (omvang) van de berekende cijfers. Hoewel de rechthoekige vorm van complexe getalnotatie handig is voor het optellen en aftrekken, is het een meer abstracte vorm van notatie dan polaire, die alleen al direct overeenkomt met echte metingen.
Impedantie (Z) van een serie RC-circuit kan worden berekend, gegeven de weerstand (R) en de capacitieve reactantie (XC ). Aangezien E=IR, E=IXC , en E =IZ, weerstand, reactantie en impedantie zijn respectievelijk evenredig met de spanning. Het spanningsfasediagram kan dus worden vervangen door een soortgelijk impedantiediagram.
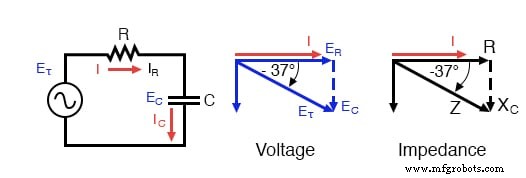
Serie:RC-circuit Impedantiefasediagram.
Voorbeeld: Gegeven:een weerstand van 40 in serie met een condensator van 88,42 microfarad. Zoek de impedantie bij 60 hertz.
XC =1/(2πfC) XC =1/(2π·60·88,42×10-6) XC =30 Ω Z =R - jXC Z =40 - j30 |Z| =sqrt(402 + (-30)2) =50 Ω ∠Z =boogtangens (-30/40) =-36,87° Z =40 - j30 =50∠-36,87°
BEOORDELING:
- Impedantie is de totale maat van weerstand tegen elektrische stroom en is de complexe (vector) som van ("echte") weerstand en ("denkbeeldige") reactantie.
- Impedanties (Z) worden op dezelfde manier beheerd als weerstanden (R) in serieschakelingsanalyse:serie-impedanties worden opgeteld om de totale impedantie te vormen. Zorg er wel voor dat u alle berekeningen in complexe (niet scalaire) vorm uitvoert! ZTotaal1 + Z2 + . . . Zn
- Houd er rekening mee dat impedanties altijd in serie worden opgeteld, ongeacht het type componenten waaruit de impedanties bestaan. Dat wil zeggen, resistieve impedantie, inductieve impedantie en capacitieve impedantie moeten wiskundig op dezelfde manier worden behandeld.
- Een puur resistieve impedantie heeft altijd een fasehoek van exact 0° (ZR =R Ω ∠ 0°).
- Een puur capacitieve impedantie heeft altijd een fasehoek van exact -90° (ZC =XC Ω ∠ -90°).
- Wet van Ohm voor AC-circuits:E =IZ; ik =E/Z; Z =E/I
- Als weerstanden en condensatoren in circuits worden gemengd, heeft de totale impedantie een fasehoek ergens tussen 0°- en -90°.
GERELATEERDE WERKBLAD:
- Werkblad serie en parallelle wisselstroomcircuits
Industriële technologie



