Theorema van Millman

In de stelling van Millman wordt de schakeling opnieuw getekend als een parallel netwerk van vertakkingen, waarbij elke vertakking een weerstand of een serie batterij/weerstand-combinatie bevat. De stelling van Millman is alleen van toepassing op die circuits die dienovereenkomstig opnieuw kunnen worden getekend. Ook hier is ons voorbeeldcircuit dat is gebruikt voor de laatste twee analysemethoden:

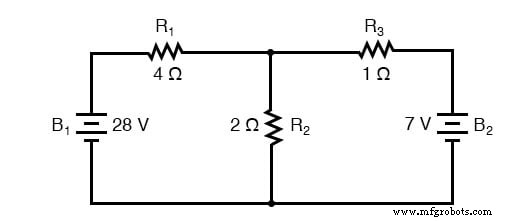
En hier is datzelfde circuit, opnieuw getekend om de stelling van Millman toe te passen:

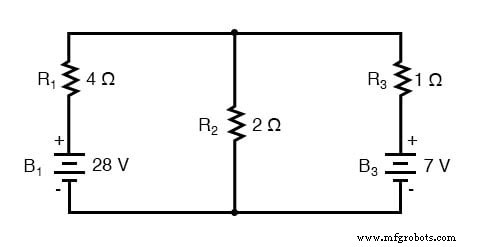
Door rekening te houden met de voedingsspanning binnen elke tak en de weerstand binnen elke tak, zal de stelling van Millman ons de spanning over alle takken vertellen. Houd er rekening mee dat ik de batterij in de meest rechtse tak heb gelabeld als "B₃ ” om duidelijk aan te geven dat het zich in de derde tak bevindt, ook al is er geen “B₂ ” in het circuit!

Theoremavergelijking van Millman

De stelling van Millman is niets meer dan een lange vergelijking, toegepast op elk circuit dat is getekend als een reeks parallel geschakelde takken, elke tak met zijn eigen spanningsbron en serieweerstand:

Door de werkelijke spannings- en weerstandscijfers uit ons voorbeeldcircuit te vervangen door de variabele termen van deze vergelijking, krijgen we de volgende uitdrukking:

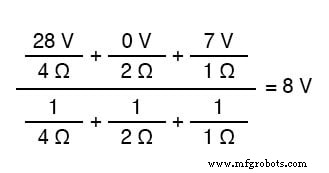
Het uiteindelijke antwoord van 8 volt is de spanning die wordt gezien over alle parallelle takken, zoals deze:

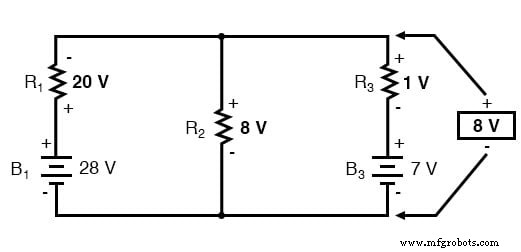
De polariteit van alle spanningen in de stelling van Millman wordt naar hetzelfde punt verwezen. In het bovenstaande voorbeeldcircuit gebruikte ik de onderste draad van het parallelle circuit als mijn referentiepunt, en dus werden de spanningen binnen elke tak (28 voor de R1-tak, 0 voor de R2-tak en 7 voor de R3-tak) ingevoegd in de vergelijking als positieve getallen. Evenzo, toen het antwoord uitkwam op 8 volt (positief), betekende dit dat de bovenste draad van het circuit positief was ten opzichte van de onderste draad (het oorspronkelijke referentiepunt). Als beide batterijen achterstevoren waren aangesloten (negatief uiteinde naar boven en positief naar beneden), zou de spanning voor tak 1 in de vergelijking zijn ingevoerd als -28 volt, de spanning voor tak 3 als -7 volt, en het resulterende antwoord van - 8 volt zou ons hebben verteld dat de bovenste draad negatief was ten opzichte van de onderste draad (ons eerste referentiepunt).

Oplossen van spanningsdalingen in de weerstand

Om weerstandsspanningsdalingen op te lossen, moet de Millman-spanning (over het parallelle netwerk) worden vergeleken met de spanningsbron binnen elke tak, met behulp van het principe van spanningen die in serie worden toegevoegd om de grootte en polariteit van de spanning over elke weerstand te bepalen:

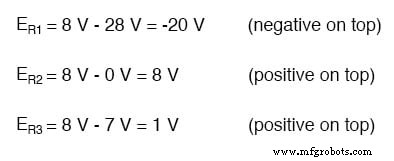
Oplossen voor takstromen

Om vertakkingsstromen op te lossen, kan elke weerstandsspanningsval worden gedeeld door zijn respectieve weerstand (I=E/R):

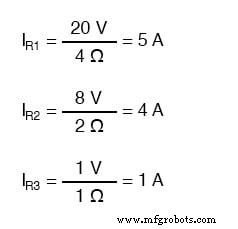
De richting van de stroom bepalen

De stroomrichting door elke weerstand wordt bepaald door de polariteit over elke weerstand, niet door de polariteit over elke batterij, aangezien de stroom terug door een batterij kan worden gedwongen, zoals het geval is bij B₃ in het voorbeeldcircuit. Dit is belangrijk om in gedachten te houden, aangezien de stelling van Millman niet zo'n directe indicatie geeft van de "verkeerde" stroomrichting als de vertakkingsstroom- of maasstroommethoden. Je moet goed letten op de polariteiten van weerstandsspanningsdalingen zoals gegeven door de spanningswet van Kirchhoff, waarmee je de richting van de stromen bepaalt.

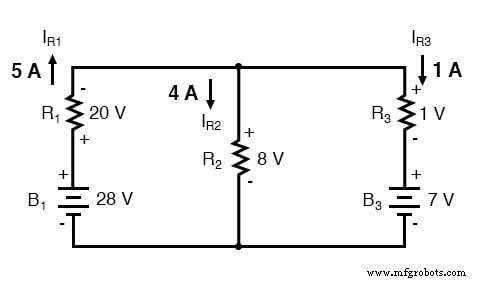
De stelling van Millman is erg handig voor het bepalen van de spanning over een reeks parallelle takken, waar voldoende spanningsbronnen aanwezig zijn om oplossing via de reguliere serie-parallelle reductiemethode uit te sluiten. Het is ook gemakkelijk in die zin dat het niet nodig is om gelijktijdige vergelijkingen te gebruiken. Het is echter beperkt omdat het alleen van toepassing is op circuits die opnieuw kunnen worden getekend om in deze vorm te passen. Het kan bijvoorbeeld niet worden gebruikt om een ​​ongebalanceerd brugcircuit op te lossen. En zelfs in gevallen waarin de stelling van Millman kan worden toegepast, kan de oplossing van individuele weerstandsspanningsdalingen voor sommigen een beetje ontmoedigend zijn, aangezien de stelling van Millman slechts een enkel cijfer geeft voor vertakkingsspanning.

Zoals u zult zien, heeft elke netwerkanalysemethode zijn eigen voor- en nadelen. Elke methode is een hulpmiddel en er is geen hulpmiddel dat perfect is voor alle taken. De bekwame technicus draagt ​​deze methoden echter in zijn of haar hoofd zoals een monteur een set gereedschappen in zijn of haar gereedschapskist draagt. Hoe meer tools je hebt uitgerust, hoe beter je voorbereid bent op elke eventualiteit.

BEOORDELING:

• De stelling van Millman behandelt circuits als een parallelle set van serie-component takken.
• Alle spanningen die zijn ingevoerd en opgelost in de stelling van Millman hebben een polariteitsreferentie op hetzelfde punt in het circuit (meestal de onderste draad van het parallelle netwerk).

GERELATEERD WERKBLAD:

• Werkblad Stelling van Millman