Superpositiestelling

De stelling van superpositie is een van die geniale streken die een complex onderwerp nemen en het vereenvoudigen op een manier die volkomen logisch is. Een stelling als die van Millman werkt zeker goed, maar het is niet helemaal duidelijk waarom het werkt zo goed. Superpositie daarentegen is duidelijk.

Serie-/parallelle analyse

De strategie die in de superpositiestelling wordt gebruikt, is om op één na alle stroombronnen binnen een netwerk tegelijk te elimineren, met behulp van serie/parallelle analyse om spanningsdalingen (en/of stromen) binnen het gewijzigde netwerk voor elke stroombron afzonderlijk te bepalen. Zodra spanningsdalingen en/of stromen zijn bepaald voor elke afzonderlijk werkende stroombron, worden de waarden allemaal "over elkaar heen gelegd" (algebraïsch toegevoegd) om de werkelijke spanningsdalingen/stromen te vinden met alle actieve bronnen. Laten we nog eens naar ons voorbeeldcircuit kijken en de superpositiestelling daarop toepassen:

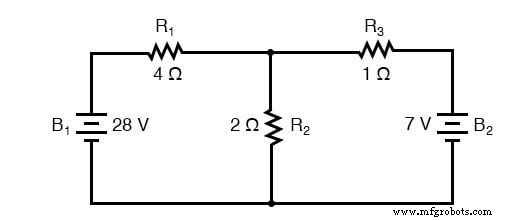
Aangezien we twee stroombronnen in dit circuit hebben, zullen we twee sets waarden voor spanningsdalingen en/of stromen moeten berekenen, één voor het circuit met alleen de 28-volt batterij in werking. . .

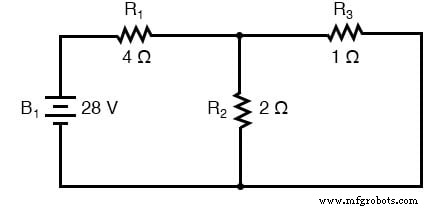
. . . en één voor het circuit met alleen de 7-volt batterij in werking:

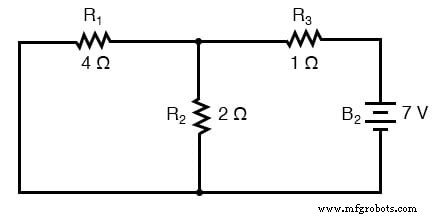
Bij het opnieuw tekenen van de schakeling voor serie-/parallelanalyse met één bron, worden alle andere spanningsbronnen vervangen door draden (kortsluitingen) en alle stroombronnen met open circuits (onderbrekingen). Omdat we in ons voorbeeldcircuit alleen spanningsbronnen (batterijen) hebben, zullen we tijdens de analyse elke inactieve bron vervangen door een draad.

Als we het circuit analyseren met alleen de 28-volt batterij, krijgen we de volgende waarden voor spanning en stroom:

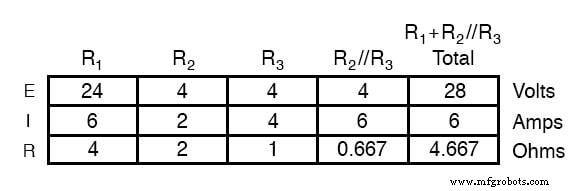
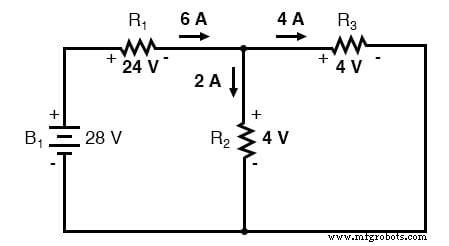
Als we het circuit analyseren met alleen de 7-volt batterij, krijgen we een andere reeks waarden voor spanning en stroom:

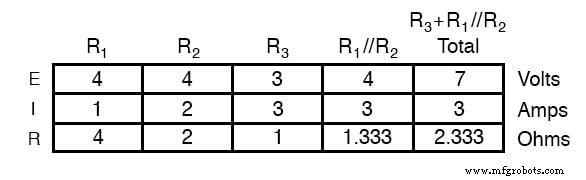
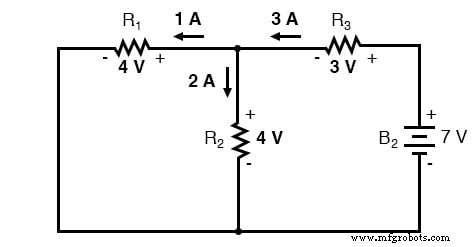
Door over elkaar heen te leggen

Bij het superponeren van deze waarden van spanning en stroom, moeten we heel voorzichtig zijn met het overwegen van polariteit (van de spanningsval) en richting (van de stroom), aangezien de waarden algebraïsch moeten worden opgeteld .

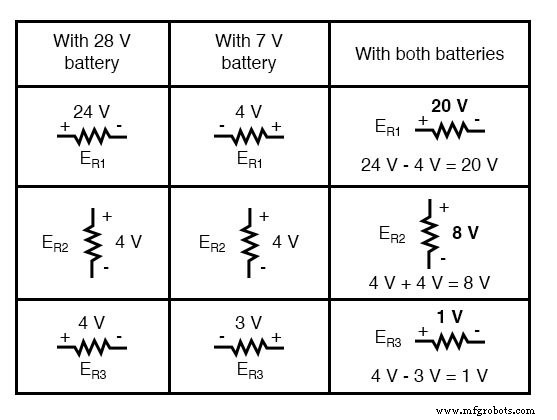
Door deze gesuperponeerde spanningscijfers op het circuit toe te passen, ziet het eindresultaat er ongeveer zo uit:

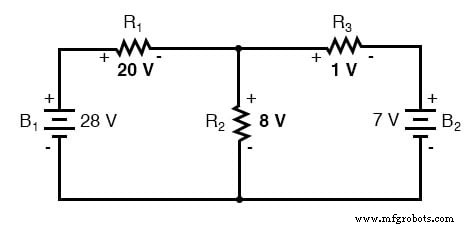
Stromen tellen ook algebraïsch op en kunnen ofwel worden gesuperponeerd zoals gedaan met de weerstandsspanningsdalingen of eenvoudig worden berekend op basis van de uiteindelijke spanningsdalingen en respectievelijke weerstanden (I=E/R). Hoe dan ook, de antwoorden zullen hetzelfde zijn. Hier zal ik de superpositiemethode laten zien die op stroom wordt toegepast:

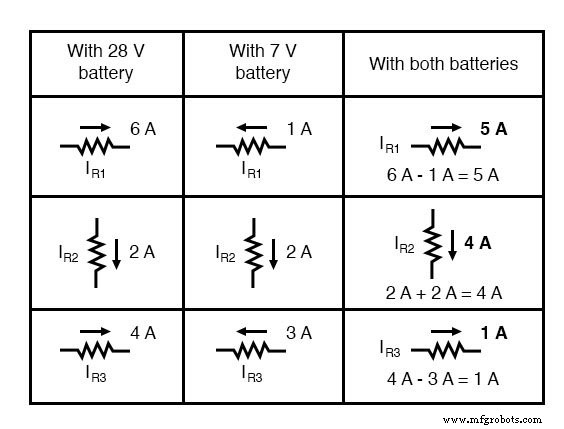
Nogmaals deze boven elkaar liggende figuren toepassen op ons circuit:

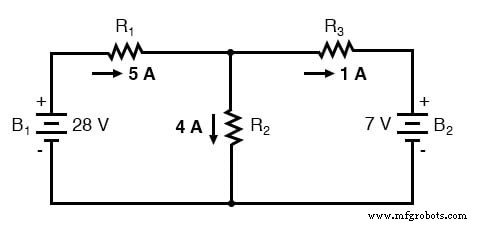
Vereisten voor de superpositiestelling

Heel eenvoudig en elegant, vind je niet? Er moet echter worden opgemerkt dat de superpositiestelling alleen werkt voor circuits die herleidbaar zijn tot serie / parallelle combinaties voor elk van de stroombronnen tegelijk (deze stelling is dus nutteloos voor het analyseren van een ongebalanceerd brugcircuit), en het is alleen werkt waar de onderliggende vergelijkingen lineair zijn (geen wiskundige krachten of wortels). De vereiste van lineariteit betekent dat de superpositiestelling alleen van toepassing is voor het bepalen van spanning en stroom, niet voor vermogen!!! Vermogensdissipaties, die niet-lineaire functies zijn, tellen niet algebraïsch op tot een nauwkeurig totaal wanneer slechts één bron tegelijk wordt beschouwd. De behoefte aan lineariteit betekent ook dat deze stelling niet kan worden toegepast in circuits waar de weerstand van een component verandert met spanning of stroom. Daarom konden netwerken met componenten zoals lampen (gloei- of gasontladingslampen) of varistoren niet worden geanalyseerd.

Een andere voorwaarde voor de superpositiestelling is dat alle componenten "bilateraal" moeten zijn, wat betekent dat ze zich hetzelfde gedragen met elektronen die er in beide richtingen doorheen stromen. Weerstanden hebben geen polariteitsspecifiek gedrag, en dus voldoen de circuits die we tot nu toe hebben bestudeerd allemaal aan dit criterium.

De superpositiestelling wordt gebruikt bij de studie van wisselstroomcircuits (AC) en halfgeleidercircuits (versterkers), waarbij AC soms vaak wordt gemengd (gesuperponeerd) met DC. Omdat AC-spannings- en stroomvergelijkingen (de wet van Ohm) lineair zijn, net als DC, kunnen we superpositie gebruiken om het circuit te analyseren met alleen de DC-stroombron en vervolgens alleen de AC-stroombron, waarbij de resultaten worden gecombineerd om te bepalen wat er zal gebeuren met zowel AC als DC-bronnen in werking. Voor nu is superpositie echter voldoende als onderbreking van het gelijktijdig uitvoeren van vergelijkingen om een ​​circuit te analyseren.

BEOORDELING:

• De superpositiestelling stelt dat een circuit kan worden geanalyseerd met slechts één stroombron tegelijk, waarbij de corresponderende componentspanningen en -stromen algebraïsch worden opgeteld om erachter te komen wat ze zullen doen met alle stroombronnen die van kracht zijn.
• Als u alle stroombronnen op één na wilt uitschakelen voor analyse, vervangt u elke spanningsbron (batterijen) door een draad; vervang elke huidige bron door een open (break).

GERELATEERD WERKBLAD:

• Superpositie Stelling Werkblad