Afgeleiden van Power Functions van e

Voorbeeld afgeleiden van e

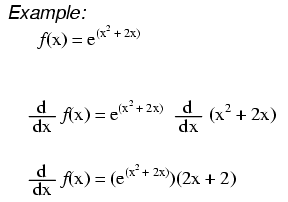
Proportionaliteitsconstante

Als we zeggen dat een relatie of fenomeen 'exponentieel' is, impliceren we dat een bepaalde hoeveelheid - elektrische stroom, winst, bevolking - sneller toeneemt naarmate de hoeveelheid groeit. Met andere woorden, de mate van verandering met betrekking tot een bepaalde variabele is evenredig met de waarde van die variabele. Dit betekent dat de afgeleide van een exponentiële functie gelijk is aan de oorspronkelijke exponentiële functie vermenigvuldigd met een constante (k ) die de evenredigheid vaststelt.

$$\frac{\text{d}}{\text{d}x}a^x=ka^x$$

De evenredigheidsconstante is gelijk aan de natuurlijke logaritme van het grondtal van de exponent:

$$\frac{\text{d}}{\text{d}x}a^x=\ln(a)\times a^x$$

Hieruit volgt dat als de natuurlijke logaritme van het grondtal gelijk is aan één, de afgeleide van de functie gelijk zal zijn aan de oorspronkelijke functie. Dit is precies wat er gebeurt met machtsfuncties van e:het natuurlijke logboek van e is 1, en bijgevolg is de afgeleide van $$e^x$$ $$e^x$$.

$$\frac{\text{d}}{\text{d}x}e^x=e^x$$

De "Ketting"-regel

Wanneer de exponentiële uitdrukking iets anders is dan alleen x, passen we de kettingregel toe:eerst nemen we de afgeleide van de hele uitdrukking, dan vermenigvuldigen we deze met de afgeleide van de uitdrukking in de exponent.

$$\frac{\text{d}}{\text{d}x}e^{x^2+2x}=e^{x^2+2x}\times\frac{\text{d}}{ \text{d}x}(x^2+2x)=(2x+2)e^{x^2+2x}$$

Deze techniek kan worden gebruikt om de veranderingssnelheid van de diodestroom ten opzichte van de diodespanning te vinden. De volgende vergelijking geeft bij benadering een relatie tussen de spanning over een diode ($$V_D$$) en de stroom door een diode ($$I_D$$):

$$I_D=I_S\times e^\frac{V_D}{0.026}$$

(Zie de pagina over diodes en gelijkrichters voor meer informatie over de diodestroom-spanningsvergelijking; merk ook op dat $$I_S$$ een constante is, geen variabele.) Om de veranderingssnelheid van stroom met betrekking tot spanning te vinden, we nemen de afgeleide:

$$\frac{\text{d}I_D}{\text{d}V_D}=\frac{\text{d}}{\text{d}V_D}(I_S\times e^\frac{V_D}{ 0.026})=I_S\times e^\frac{V_D}{0.026}\times\frac{1}{0.026}$$

Dus, bij een gegeven waarde van de diodespanning $$V_D$$, zal een toenemende spanningstoename een stroomtoename creëren gelijk aan $$\frac{I_S}{0.026}e^\frac{V_D}{0.026}$$ .

GERELATEERDE WERKBLAD:

• Rekenblad voor elektrische circuits