Kanaalplasmonnanodraadlasers met V-groefholten

Abstract

Een hybride kanaalplasmon-nanodraadlaser op basis van GaAs/AlGaAs kern-schil halfgeleider nanodraad en zilveren V-groef wordt voorgesteld. De laserstructuur heeft het potentieel om te integreren met plasmonische golfgeleiders, met behulp van kanaalplasmon-polaritonmodi in V-groef plasmonische golfgeleiders. Geleidende en lasereigenschappen worden numeriek berekend met behulp van de eindige-elementenmethode. Op basis van de theoretische resultaten zou de laser de geleidingsmodus kunnen ondersteunen met een kleinste diameter van 40 nm. Laseremissie kan plaatsvinden bij een relatief lage drempel rond 2000 cm^− 1 wanneer de diameter groter is dan 140 nm. Een vrij grote Purcell-factor van 180 zou kunnen worden bereikt om de spontane emissie te verhogen.

Achtergrond

Met cilindrische geometrie en sterke tweedimensionale opsluiting van elektronen, gaten en fotonen, is onafhankelijke halfgeleider nanodraad ideaal voor halfgeleiderlaser met verminderde drempel en compact formaat [1,2,3,4,5,6]. Tot op heden is laseremissie bij kamertemperatuur gerealiseerd in ZnO-, GaN-, CdS- en GaAs-nanodraden, die een optisch spectrum bestrijken van ultraviolet tot bijna-infrarood [7,8,9,10,11,12]. Om de afmetingen van nanodraden voorbij de diffractielimiet voort te zetten, zijn plasmonische nanodraadlasers voorgesteld en experimenteel gedemonstreerd, waaronder hybride plasmonische nanodraadlasers en plasmonnanodraadlasers van hoge orde [13,14,15]. Onder hen bereikten hybride plasmonische nanodraadlasers een veel kleinere dimensielimiet. Onlangs toonde plasmonische nanodraadlaser zijn vermogen om te integreren met plasmonische golfgeleiders, met behulp van kanaalplasmon-polariton (CPP) -modi in V-groef plasmonische golfgeleiders [16]. De diameters die in het experiment zijn aangenomen, liggen boven 300 nm. CPP's zijn de plasmonpolaritonen die worden geleid door een V-vormige groef die in metaal is uitgehouwen, wat voor het eerst theoretisch werd gesuggereerd door Maradudin en collega's [17]. CPP's vertoonden sterke opsluiting, lage demping en robuustheid tegen kanaalbuiging bij nabij-infrarode golflengten [18,19,20].

Hier, door de lage dissipatie van hybride plasmonische modi te combineren met de sterke opsluiting en integratie met plasmonische golfgeleiders van CPP-modus, stellen we een hybride kanaalplasmon-nanodraad (CPN) -lasers voor en onderzoeken numeriek de modale en laserende eigenschappen. De CPN-laser bestaat uit een GaAs/AlGaAs-nanodraad in de kern en een zilveren V-groef die wordt gescheiden door een ultradunne diëlektrische laag van MgF₂ , waarbij de diameter van nanodraad zich in het bereik van 40 tot 220 nm bevindt om de lasereigenschappen buiten de diffractielimiet te onderzoeken. Vanwege de zeshoekige vorm van GaAs/AlGaAs-nanodraad, worden in het volgende gedeelte twee geïntegreerde structuren van CPN-lasers getoond.

PPN-laserstructuren

Het schema van de CPN-laserstructuren wordt gedemonstreerd in Fig. 1, waar het achtergrondmateriaal lucht is, het grijze materiaal zilver, waarvan de permittiviteit wordt beschreven door het Drude-model $ {\varepsilon}_r={\varepsilon}_{ \infty }-{\omega}_p^2/\left({\omega}^2+ j\gamma \omega \right) $, met ε _∞ =3.7, ω _p =9.1 eV, en γ =0,018 eV [21]. De nanodraad die in de V-groef ligt, heeft een kern-schaalstructuur, het kernmateriaal is GaAs en het schaalmateriaal is AlGaAs. De GaAs-kern wordt gepassiveerd door een dunne AlGaAs-schillaag van 10 nm om de stralingsefficiëntie te verbeteren [12]. Tussen de nanodraad en de V-groef bevindt zich een ultradunne diëlektrische laag van MgF₂ . De dikte is vastgesteld op 5 nm om verspreiding met weinig verlies onder sterke optische opsluiting te ondersteunen. Er zijn twee manieren om CPN-lasers te integreren. De eerste noemen we het CPN-N (CPN-smalle hoek) zoals weergegeven in Fig. 1a, c, waar de nanodraad horizontaal op het oppervlak van de V-groef ligt met een kleine hoek van 60 °. De nanodraad heeft twee kanten contact met de diëlektrische laag en het V-groefoppervlak, tussen de onderkant en het hoekpunt van de V-groef is lucht. De tweede noemen we het CPN-W (CPN-groothoek) zoals weergegeven in Fig. 1b, d, waar de nanodraad verticaal op het oppervlak van de V-groef ligt met een brede hoek van 120°. De nanodraad heeft niet alleen tweezijdig contact, maar ook een topcontact met de diëlektrische laag en het V-groefoppervlak.

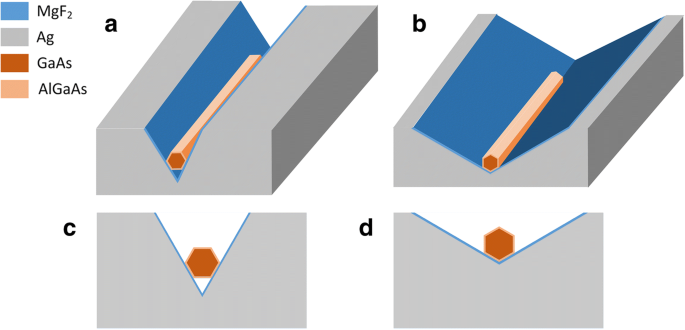
Schematisch diagram van de CPN-laserstructuren. een CPN-N. b CPN-W. c Dwarsdoorsnede van CPN-N. d Dwarsdoorsnede van CPN-W

Ondersteunde CPP-modi in de V-groef zijn afhankelijk van de hoek en diepte van de groef, vooral de hoek. Normaal gesproken neemt het aantal CPP-modi dat door de groef wordt ondersteund af met toenemende hoeken, en in een eindig diepe groef kan er geen CPP in de groef bestaan als de graad groter is dan de kritische graad [22]. Een sterke lokalisatie van CPP kan worden bereikt in groeven met voldoende kleine hoeken [23], wat ook wordt getoond in Fig. 2. In Fig. 2a-c is de groefdiepte vastgesteld op 1 m, de groefhoeken zijn 10° respectievelijk , 30° en 60°. Elektrisch veld is sterk gelokaliseerd in de bodem van de groef met 10°, waardoor de CPP-modus wordt gevormd. Terwijl het elektrische veld zich met 30 ° naar de rand van de groef begint te verspreiden, wat aangeeft dat de lokalisatie veel zwakker wordt. Met de verhoogde groefhoek tot 60°, bestaat er geen CPP in de groef. Echter, zoals getoond in Fig. 2d, e, met de integratie van nanodraad, bestaat CPP nog steeds in een groothoek van 60 ° en 120 ° (diepte is kleiner dan 1 m) en strak gelokaliseerd in de laag-diëlektrische MgF₂ laag, die totaal anders is dan normale groeven. In een hybride plasmonische structuur zoals CPN-holte, maakt de koppeling tussen diëlektrische en plasmonische modi over de ultradunne diëlektrische laag 'condensatorachtige' energieopslag mogelijk die subgolflengtelichtpropagatie mogelijk maakt in niet-metalen gebieden met nanogelokaliseerd elektromagnetisch veld [24]. Het elektrische veld van CPP is dus sterk gelokaliseerd in de MgF₂ spleet tussen nanodraad en groef, zelfs in de groef met grote hoeken. Verdere geleidings- en lasereigenschappen in CPN-N- en CPN-W-lasers zullen in de volgende sectie worden uitgewerkt.

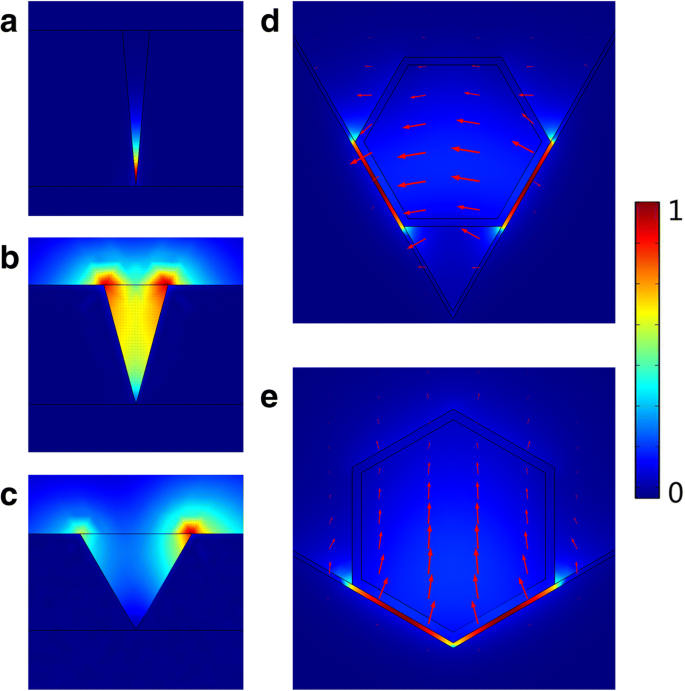
Elektrisch velddistributie in a groef met 10°. b Groef met 30°. c Groef met 60°. d CPN-N-laser. e CPN-W-laser. De rode pijlen geven de oriëntatie van het elektrische veld aan

Resultaten en discussie

Met het voordeel van hybride plasmonische modi, kan het elektrische veld worden gelokaliseerd in afmetingen buiten de diffractielimiet met propagatie met weinig verlies [25, 26]. Ons onderzoek richt zich dus op de geleidings- en lasereigenschappen in de afmetingen van de subgolflengtediameter, 40 tot 220 nm. Hoewel het een uitdaging is om de positie van nanodraad met een diameter van minder dan 100 nm nauwkeurig te controleren, wordt hier een min of meer ideale toestand beschouwd om de potentiële prestaties van CPN-lasers te onderzoeken.

Net als andere plasmonische nanodraadlasers, worden meer geleide modi ondersteund in CPN-lasers met toenemende diameters van nanodraden. Zoals weergegeven in figuur 3, kan de nanodraad met een diameter van 200 nm die in de groef is verwerkt, vier geleide modi ondersteunen, HE_11x , HE_11j , TE₀₁ , en TM₀₁ . Het oppervlak van de groef is evenwijdig aan de zijkanten van nanodraad, dus de groefhoek blijft onveranderlijk als de diameter van de nanodraad verandert. In een plasmonische nanodraadlaser met een vlak substraat heeft de nanodraad slechts één zijcontact met het substraat, wat leidt tot de koppeling tussen alleen fotonische modi van HE_11y en oppervlakteplasmonen. Terwijl in een CPN-structuur beide HE_11x en HE_11y koppel met oppervlakteplasmonen die hybride kanaalplasmonische modi vormen vanwege tweezijdig contact tussen de nanodraad en het oppervlak van de groef. Voor modi TE₀₁ en TM₀₁ , elektromagnetische energie in de nanodraad koppelt ook met de oppervlakteplasmonen op het groefoppervlak en vormt kanaalplasmonische modi. De bovenstaande vier modi zijn de geleide modi in CPN-lasers met een diameter van 200 nm, en de modi worden afgesneden met de afnemende diameter.

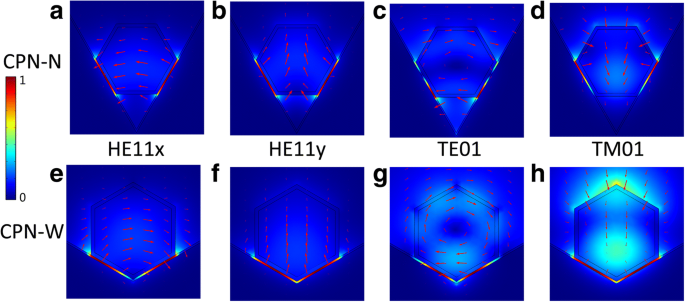
Elektrisch veldverdeling van modi in CPN-N laser (a –d ) en CPN-W laser (e –u ). De diameter van de nanodraad is vastgesteld op 200 nm

Onderzoek naar de geleidende en laserende eigenschappen van de CPN-laser, afhankelijkheden van het reële deel van effectieve index, modaal verlies, modale opsluitingsfactor en drempelversterking op de nanodraaddiameter D worden berekend en weergegeven in Fig. 4a-d. Modi HE_11x , HE_11j , TE₀₁ , en TM₀₁ van CPN-N- en CPN-W-lasers worden hier allemaal onderzocht. Eigenschappen van CPN-N- en CPN-W-lasers zijn respectievelijk gemarkeerd als bloksymbool met ononderbroken lijn en cirkelsymbool met stippellijn. Het is de moeite waard om op te merken dat de groefdiepte hier veel groter is dan de nanodraaddiameter om de invloed van de groefrand te elimineren. Zoals weergegeven in figuur 4a, is er een positieve correlatie tussen het reële deel van de effectieve indices Re(n _eff ) en nanodraaddiameter D . Dit gedraagt zich hetzelfde als de effectieve index van een individuele nanodraad. Met de toenemende diameter van nanodraad wordt de equivalente index van de structuur groter, wat leidt tot de toenemende modale index. Naarmate de diameter kleiner wordt, modus TE₀₁ van de CPN-W-laser wordt eerst afgesneden bij 200 nm, daarna modus TM₀₁ van CPN-W-laser snijdt af bij 180 nm, en modi TE₀₁ en TM₀₁ van de CPN-N-laser beide afgesneden op 170 nm, terwijl de fundamentele modi HE_11x en HE_11y kleinere afsnijdiameters hebben. Door de asymmetrische structuur van CPN-lasers degenereert de fundamentele modus niet meer. Modus HE_11x heeft de kleinste afsnijdiameter van 40 nm tijdens alle modi in een CPN-N-laser. Modus HE_11j heeft de kleinste afsnijdiameter van 80 nm tijdens alle modi in een CPN-W-laser. In een CPN-N laser, Re(n _eff ) van modus HE_11x is groter dan die van modus HE_11y . Terwijl in een CPN-W-laser Re(n _eff ) van modus HE_11y is groter dan die van modus HE_11x , die het gevolg is van de loodrechte component van de fundamentele modus. Normaal gesproken zijn de richtingen van het elektrische veld van HE_11x en TE₀₁ staan loodrecht op HE_11y en TM₀₁ , respectievelijk. In CPN-N- en CPN-W-lasers zijn de groefhoeken 60° en 120°, waardoor x -component van modi domineert in CPN-N lasers en y -component van modi domineert in CPN-W-lasers, zoals weergegeven in figuur 2d, e. Dus modi HE_11x en TE₀₁ hebben grotere Re(n _eff ) en kleinere afsnijdiameters in een CPN-N-laser, terwijl modi HE_11y en TM₀₁ hebben grotere Re(n _eff ) en kleinere afsnijdiameter in een CPN-W laser.

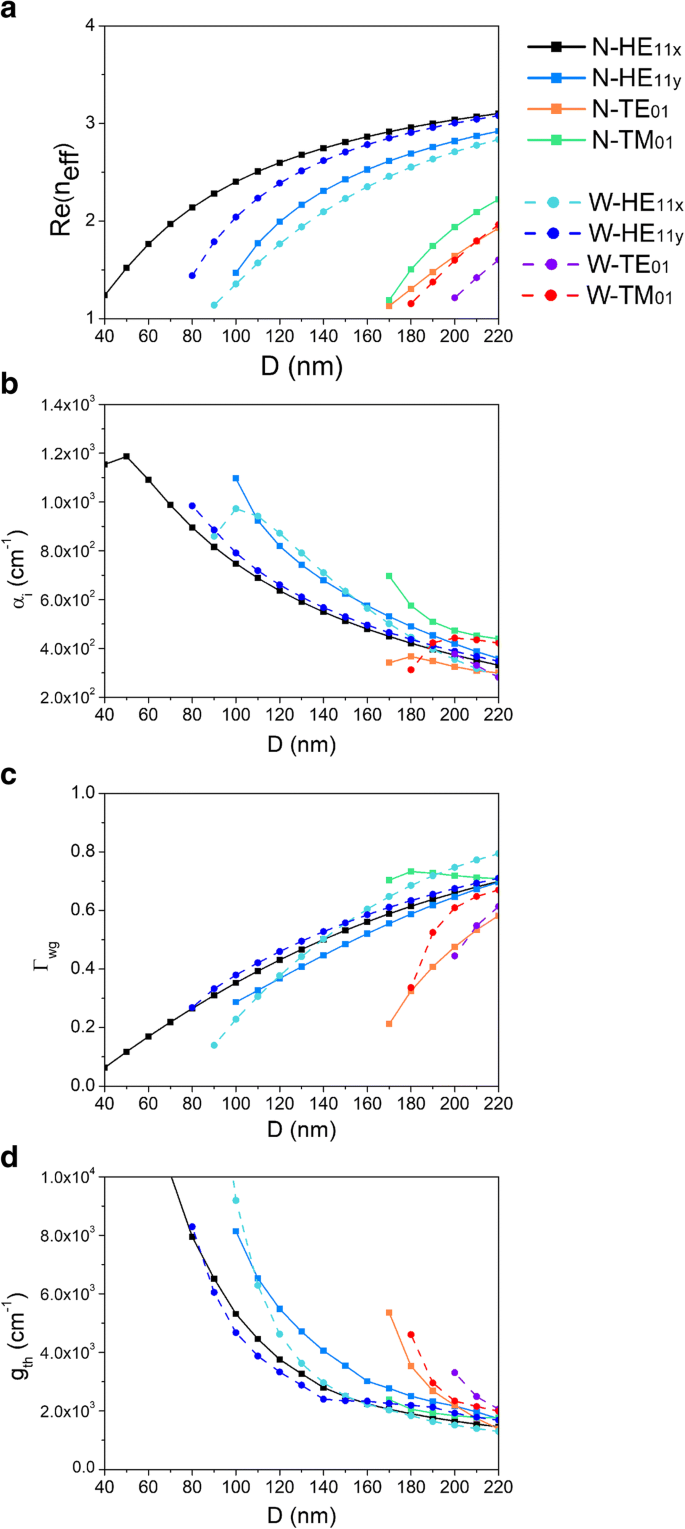
Afhankelijkheden van a het reële deel van de effectieve index, b modaal verlies, c modale beperkingsfactor, en d drempelversterking op nanodraaddiameter D

Het modale verlies per lengte-eenheid α _ik en modale opsluitingsfactor Γ _wg zijn belangrijke factoren van de optische holte die relevant zijn voor laseren. De modale beperkingsfactor is een indicator van hoe goed de modus overlapt met het versterkingsmedium, dat wordt gedefinieerd als de verhouding tussen de modale versterking en de materiële versterking in het actieve gebied [27, 28]. Het modale verlies per lengte-eenheid α _ik kan worden verkregen uit het denkbeeldige deel van de modale voortplantingsconstante k _z als α _ik = 2 Im[k _z ]. Zoals weergegeven in figuur 4b, gedraagt het modale verlies van CPN-N- en CPN-W-lasers zich negatief gecorreleerd met de nanodraaddiameter D . Terwijl, zoals weergegeven in figuur 4c, de opsluitingsfactor van CPN-N- en CPN-W-lasers zich positief gecorreleerd heeft met de nanodraaddiameter D . Met de afnemende diameter van nanodraad kan de elektromagnetische energie niet goed worden gelokaliseerd in de nanodraad, er lekt steeds meer elektromagnetische energie. Een deel van de elektromagnetische energie verstrooit naar buiten vanaf het bovenste deel van nanodraad, en een deel van de energie interageert met het groefoppervlak, wat leidt tot meer metaaldissipatie. Het is interessant om op te merken dat modus TM₀₁ in CPN-N heeft laser zowel een relatief grote opsluitingsfactor als modaal verlies. Dit kan worden toegeschreven aan de verdeling van het elektrisch veld van modus TM₀₁ . Zoals te zien is in figuur 3d, verdeelt elektromagnetische energie zich zowel in de nanodraad als rond het oppervlak ervan. Hoewel de opsluiting strakker is, heeft de elektromagnetische energie een sterkere interactie met de metalen groef. Belangrijk is dat in figuur 4c, naarmate de diameter van de nanodraad toeneemt, de opsluitingsfactor groter wordt, wat aangeeft dat de elektromagnetische energie in de holte is opgesloten en goed overlapt met het actieve gebied en mogelijk de laserdrempel verlaagt.

De laserdrempel is het laagste excitatieniveau waarbij de laseroutput wordt gedomineerd door gestimuleerde emissie in plaats van spontane emissie. De drempelversterking g _de , die de vereiste versterking per lengte-eenheid voor laseren beschrijft, wordt gedefinieerd als $ {g}_{\mathrm{th}}=\frac{1}{\varGamma_{wg}}\left[{\alpha}_i+\ frac{1}{L}\ln \left(\frac{1}{R}\right)\right] $, waarbij R geeft het geometrische gemiddelde aan van de reflectiviteit van de eindfacetten van nanodraad en L is de lengte van de nanodraad F-P-holte [29]. De lengte L is vastgesteld op 10 μm, wat past bij de experimentele gegevens in Ref. [12]. Opgemerkt moet worden dat de nanodraad hier hetzelfde is als Ref. [11, 12], waarin de gegroeide methode van Au-deeltjeskatalysator werd toegepast. Er zit dus een gouden dop op de bovenkant van nanodraad. Voor het eindfacet met een gouden dop is de reflectiviteit groter dan het andere eindfacet, rond en meer dan 70%. We tonen de afhankelijkheid van drempelversterking g _de op D in figuur 4d. Het is duidelijk dat de drempelversterking afneemt met de toenemende diameter van de nanodraad. Dit komt overeen met het gedrag van modaal verlies en opsluitingsfactor, die sleutelfactoren zijn voor drempelversterking. Naarmate de diameter van de nanodraad groter wordt, wordt de elektromagnetische energie beter opgesloten in de nanodraad, wat leidt tot een grotere opsluitingsfactor en minder verlies van energielekkage. De drempelversterking wordt dus lager. In een kleiner diameterbereik, de drempelversterking van modus HE_11x is lager dan modus HE_11y in CPN-N laser, de drempelversterking van modus HE_11y is lager dan modus HE_11x in CPN-W-laser. Dit bewijst ook de modus HE_11x en HE_11y draait in CPN-lasers, vanwege het effect van groefhoeken op de elektrische veldcomponenten.

Kwaliteitsfactor Q van een holtemodus is een indicatie van hoe lang de opgeslagen energie van die modus in de holte blijft wanneer interbandovergangen afwezig zijn, wat gerelateerd is aan de levensduur van het foton τ _p voert de snelheidsvergelijking in via de resonantiefrequentie ω van de modus. Voor een FP-caviteit wordt de kwaliteitsfactor gedefinieerd in de sectie methoden [30]. Een hoge kwaliteitsfactor duidt op een lage snelheid van energieverlies ten opzichte van de opgeslagen energie van de holte en de oscillaties sterven langzaam uit. Het apparaat kan dus bij een lagere drempel werken en dus kan het pompvermogen worden verminderd. We verbeelden Q factor als functies van D in afb. 5a. Er zijn positieve correlaties tussen kwaliteitsfactoren van alle modi en diameter D , behalve voor modi TM₀₁ in CPN-N- en CPN-W-lasers. Dit kan worden toegeschreven aan de elektrische veldverdeling van modus TM₀₁ , die hierboven is besproken. Bovendien hangt de spontane emissiesnelheid in een nanolaser zoals CPN-laser gedeeltelijk af van de omgeving van een lichtbron. Volgens de gouden rol van Fermi is de spontane emissiesnelheid van een emitter evenredig met de lokale dichtheid van optische toestanden (LDOS) [31]. In een omgeving die structuur is op de schaal van de golflengte, kan de LDOS ruimtelijk worden bestuurd [32]. Dientengevolge kan de LDOS van een emitter lokaal worden verhoogd samen met de snelheid van spontane emissie of worden verlaagd door de microholte onder de golflengte, wat het Purcell-effect wordt genoemd [33]. De nanogelokaliseerde elektromagnetische energie kan de laserdrempel verlagen door de spontane emissiesnelheid te verhogen via het Purcell-effect. In CPN-N- en CPN-W-lasers is elektromagnetische energie strak gelokaliseerd op subgolflengteschaal, wat resulteert in grote Purcell-factoren zoals weergegeven in figuur 5b. De metalen groef wijzigt de diëlektrische omgeving rond de nanodraad en construeert een subgolflengteholte, waardoor een ultraklein volume en koppeling tussen een exciton en een microcavity-modus mogelijk wordt. Met de afnemende diameter neemt de Purcell-factor sterk toe en bereikt meer dan 100. Bovendien kan een grote LDOS niet alleen de snelheid van spontane emissie verhogen, maar ook het gestimuleerde emissieproces in de laserwerking verhogen. Laserwerking zou gemakkelijker kunnen worden bereikt omdat het nanogelokaliseerde elektromagnetische veld van de hybride plasmonische modus niet alleen de excitonen in de nanolaser snel laat diffunderen naar gebieden met snellere recombinatie, waardoor de overlap tussen materiaalversterking en plasmonische modus wordt verbeterd, maar ook aangeslagen deeltjes stimuleert om energie over te dragen in plasmonen met dezelfde frequentie, fase en polarisatie. Om de subgolflengte-lokalisatieschaal te kwantificeren, werd het genormaliseerde modale gebied berekend met behulp van de methode in Ref. [13] en weergegeven in Fig. 5c. In vergelijking met figuur 5b is de Purcell-factor omgekeerd evenredig met het genormaliseerde modale gebied, wat aantoont dat de holte op subgolflengteschaal de Purcell-factor verhoogt en daardoor de spontane emissiesnelheid verhoogt.

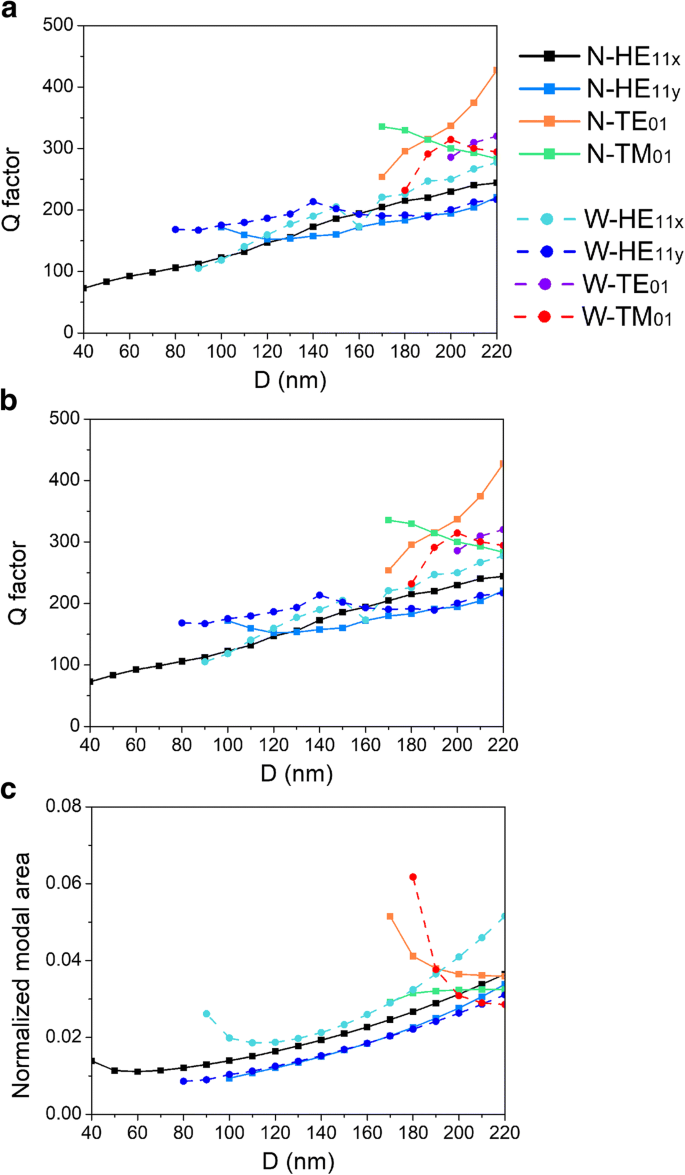
Afhankelijkheden van a kwaliteitsfactor, b Purcell-factor, en c genormaliseerd modaal gebied op nanodraaddiameter D

Conclusies

We hebben een CPN-laserstructuur voorgesteld op basis van halfgeleider nanodraad en metalen V-groef samen met een ultradunne laag diëlektricum. Met de aanwezigheid van nanodraad met hoge index kunnen kanaalplasmonen in de groeven voorkomen met relatief grote hoeken die hybride kanaalplasmonische modi vormen. De metalen groef wijzigt de diëlektrische omgeving rond de nanodraad en construeert een holte onder de golflengte die de spontane emissiesnelheid verbetert. Geleidende en lasereigenschappen werden onderzocht met behulp van de eindige-elementenmethode. De fundamentele modus HE_11x in CPN-N laser heeft een zeer kleine afsnijdiameter, waardoor ultrakleine voetafdruk van on-chip lasers mogelijk is. Met het voordeel van hoge opsluiting en ultraklein genormaliseerd modaal gebied, kan de Purcell-factor meer dan 150 bereiken om de spontane emissie aanzienlijk te verbeteren. Bovendien heeft deze CPN-laser ook het potentieel om te integreren met plasmonische golfgeleiders met behulp van CPP-modi in V-groef plasmonische golfgeleiders, die belangrijke toepassingen zouden vinden in optische onderlinge verbindingen op de chip.

Methoden/experimenteel

Leidende en lasereigenschappen werden numeriek berekend met behulp van de eindige-elementenmethode met de verstrooiingsrandvoorwaarde in de frequentie, wat een veelgebruikte benadering is om de noodzakelijke open grens na te bootsen. De elektrische veldverdelingen van de eigenmodes van CPN-lasers worden direct verkregen door mode-analyses. De geleidingseigenschappen worden berekend door de complexe voortplantingsconstante met β + iα . Het reële deel van de modale effectieve index wordt berekend door n _eff = Re(n _eff ) = β /k ₀ , waar k ₀ is de vacuümgolfvector. Het effectieve modusgebied wordt berekend met [24]

$$ {A}_m=\frac{W_m}{\max \left\{W(r)\right\}}=\frac{1}{\max \left\{W(r)\right\}} {\iint}_{\infty }W(r){d}^2r $$ (1)

waar W _m is de totale modus energie en W(r) is de energiedichtheid (per lengte-eenheid gestroomd langs de voortplantingsrichting). Voor dispersieve en lossy materialen, de W(r) binnen kan worden berekend met behulp van Vgl. (2):

$$ W(r)=\frac{1}{2}\left(\frac{d\left(\varepsilon (r)\omega \right)}{d\omega}{\left|E(r)\ rechts|}^2+{\mu}_0{\left|H(r)\right|}^2\right) $$ (2)

Kwaliteitsfactor en Purcell worden gedefinieerd als [30, 33]

$$ \kern0.75em \frac{1}{Q}=\frac{1}{{\omega \tau}_p}=\frac{\nu_{g,z}\left(\omega \right)}{ \omega}\left[{\alpha}_i+\frac{1}{L}\ln \left(\frac{1}{R}\right)\right] $$ (3) $$ {F}_p=\frac{3}{4{\pi}^2}{\left(\frac{\lambda }{n}\right)}^3\left(\frac{Q}{V_{eff}}\right) $$ (4)

Vergelijkingen voor het berekenen van modaal verlies, modale opsluitingsfactor en drempelversterking worden gegeven in de hoofdtekst; we vertellen hier niet meer.

Afkortingen

CPN:: Kanaalplasmon nanodraad
CPN-N:: Kanaalplasmon nanodraad-smalle-hoek
CPN-W:: Kanaalplasmon nanodraad-groothoek
CPP:: Kanaalplasmon-polariton

Potentiële dip in organische fotovoltaïsche energie, onderzocht door cross-sectionele Kelvin Probe Force Microscopy Effecten van etsvariaties op Ge/Si-kanaalvorming en apparaatprestaties

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal