Meer over spectrumanalyse

Geautomatiseerde Fourier-analyse, met name in de vorm van de FFT algoritme, is een krachtig hulpmiddel om ons begrip van golfvormen en hun gerelateerde spectrale componenten te vergroten.

Dezelfde wiskundige routine die in de SPICE-simulator is geprogrammeerd als de .fourier-optie, is ook geprogrammeerd in een verscheidenheid aan elektronische testinstrumenten om realtime Fourier-analyse uit te voeren op gemeten signalen.

Deze sectie is gewijd aan het gebruik van dergelijke tools en de analyse van verschillende golfvormen.

Ten eerste hebben we een eenvoudige sinusgolf met een frequentie van 523,25 Hz. Deze specifieke frequentiewaarde is een “C”-toonhoogte op een pianotoetsenbord, één octaaf boven de “middelste C”.

In feite werd het signaal dat voor deze demonstratie werd gemeten, gecreëerd door een elektronisch toetsenbord dat de toon van een panfluit produceerde, de 'stem' van het instrument die het dichtst in de buurt kwam van een perfecte sinusgolf. De onderstaande grafiek is afkomstig van een oscilloscoopscherm en toont de signaalamplitude (spanning) in de loop van de tijd:

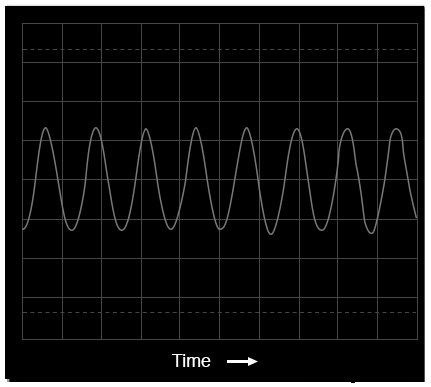
Oscilloscoopweergave:spanning versus tijd

Bekeken met een oscilloscoop, ziet een sinusgolf eruit als een golvende curve die horizontaal op het scherm wordt getekend. De horizontale as van dit oscilloscoopscherm is gemarkeerd met het woord "Tijd" en een pijl die in de richting van de voortgang van de tijd wijst. De curve zelf vertegenwoordigt natuurlijk de cyclische toename en afname van de spanning in de loop van de tijd.

Nauwkeurige observatie onthult onvolkomenheden in de sinusgolfvorm. Dit is helaas een gevolg van de specifieke apparatuur die wordt gebruikt om de golfvorm te analyseren. Kenmerken zoals deze als gevolg van eigenaardigheden van de testapparatuur zijn technisch bekend als artefacten :verschijnselen die uitsluitend bestaan ​​vanwege een eigenaardigheid in de apparatuur die wordt gebruikt om het experiment uit te voeren.

Als we dezelfde wisselspanning bekijken op een spectrumanalysator, is het resultaat heel anders:

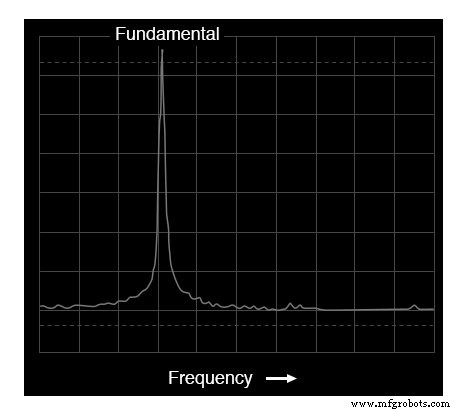
Spectrumanalysatorweergave:spanning versus frequentie

Zoals u kunt zien, is de horizontale as van het display gemarkeerd met het woord "Frequentie", waarmee het domein van deze meting wordt aangeduid. De enkele piek op de curve vertegenwoordigt de overheersing van een enkele frequentie binnen het frequentiebereik dat door de breedte van het scherm wordt bestreken.

Als de schaal van dit analyse-instrument met cijfers was gemarkeerd, zou je zien dat deze piek optreedt bij 523,25 Hz. De hoogte van de piek vertegenwoordigt de signaalamplitude (spanning).

Als we drie verschillende sinusgolftonen met elkaar mengen op het elektronische toetsenbord (C-E-G, een C-majeur akkoord) en het resultaat meten, weerspiegelen zowel het oscilloscoopdisplay als het spectrumanalysatordisplay deze toegenomen complexiteit:

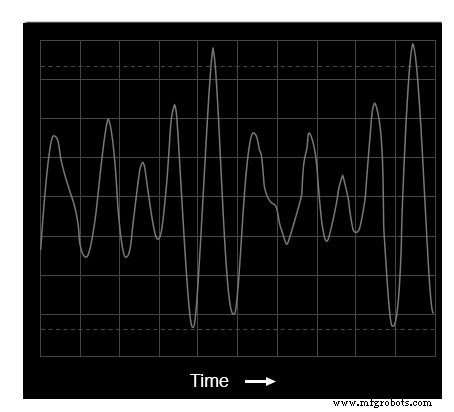
Oscilloscape-weergave:drie tonen

De oscilloscoopweergave (tijddomein) toont een golfvorm met veel meer pieken en dalen dan voorheen, een direct gevolg van de vermenging van deze drie frequenties. Zoals je zult zien, zijn sommige van deze pieken hoger dan de pieken van de originele single-pitch golfvorm, terwijl andere lager zijn.

Dit is het resultaat van de drie verschillende golfvormen die elkaar afwisselend versterken en opheffen wanneer hun respectievelijke faseverschuivingen in de tijd veranderen.

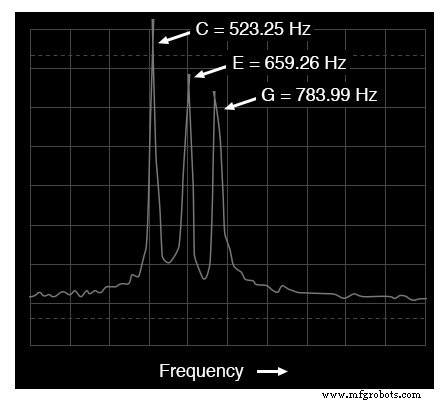
Spectrumanalyzerweergave:drie tonen

De spectrumweergave (frequentiedomein) is veel gemakkelijker te interpreteren:elke toonhoogte wordt weergegeven door zijn eigen piek op de curve. Het hoogteverschil tussen deze drie pieken is een ander artefact van de testapparatuur:een gevolg van beperkingen binnen de apparatuur die wordt gebruikt om deze golfvormen te genereren en te analyseren, en niet een noodzakelijk kenmerk van het muzikale akkoord zelf.

Zoals eerder vermeld, is het apparaat dat wordt gebruikt om deze golfvormen te genereren een elektronisch toetsenbord:een muziekinstrument dat is ontworpen om de tonen van veel verschillende instrumenten na te bootsen.

De panfluit "stem" werd gekozen voor de eerste demonstraties omdat deze het meest leek op een zuivere sinusgolf (een enkele frequentie op het spectrumanalysatorscherm). Andere "stemmen" van muziekinstrumenten zijn echter niet zo eenvoudig als deze. In feite is de unieke toon geproduceerd door elke instrument is een functie van zijn golfvorm (of spectrum van frequenties).

Laten we bijvoorbeeld het signaal voor een trompettoon bekijken:

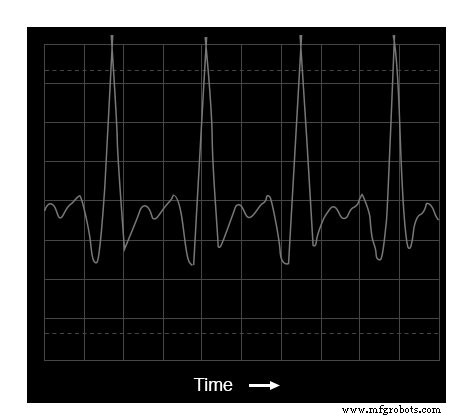
Oscilloscoopweergave:golfvorm van een trompettoon

De grondfrequentie van deze toon is hetzelfde als in het eerste voorbeeld van de panfluit:523,25 Hz, één octaaf boven "middelste C".

De golfvorm zelf is verre van een pure en eenvoudige sinusgolfvorm. Wetende dat elke herhalende, niet-sinusvormige golfvorm gelijk is aan een reeks sinusvormige golfvormen met verschillende amplitudes en frequenties, zouden we meerdere pieken op het spectrumanalysator-display moeten verwachten:

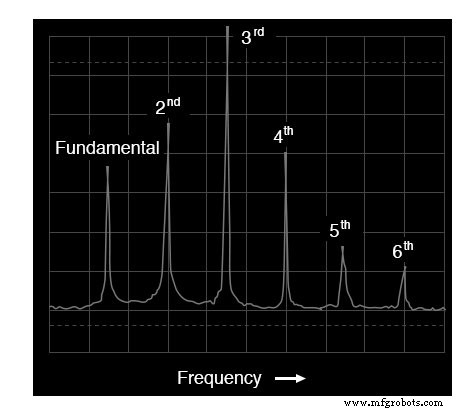
Spectrum van een trompettoon

Dat doen we inderdaad! De fundamentele frequentiecomponent van 523,25 Hz wordt weergegeven door de meest linkse piek, waarbij elke opeenvolgende harmonische wordt weergegeven als zijn eigen piek langs de breedte van het scherm van de analysator.

De tweede harmonische is tweemaal de frequentie van de grondtoon (1046,5 Hz), de derde harmonische driemaal de grondtoon (1569,75 Hz), enzovoort. Dit display toont alleen de eerste zes harmonischen, maar er zijn er veel meer die deze complexe toon omvatten.

Door een andere instrumentstem (de accordeon) op het toetsenbord te proberen, verkrijgen we een even complexe oscilloscoop (tijddomein) plot en spectrumanalysator (frequentiedomein) weergave:

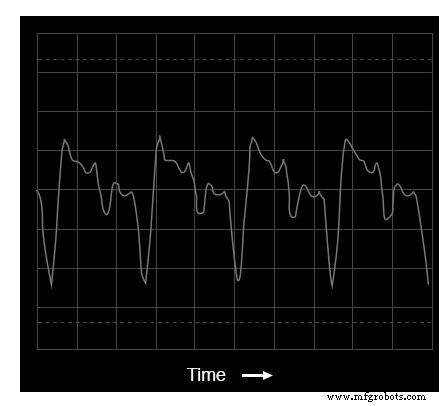
Oscilloscoopweergave:golfvorm van accordeontoon

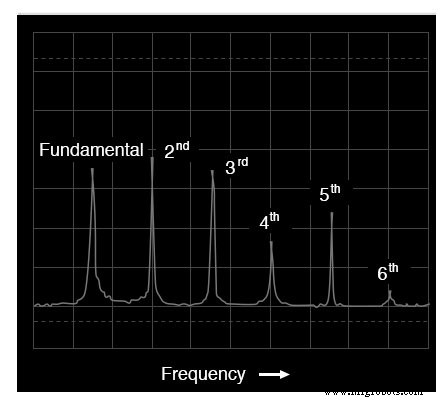
Spectrum van accordeontoon

Let op de verschillen in relatieve harmonische amplituden (piekhoogten) op de spectrumdisplays voor trompet en accordeon. Beide instrumenttonen bevatten harmonischen helemaal van 1e (fundamentele) tot 6e (en verder!), maar de verhoudingen zijn niet hetzelfde.

Elk instrument heeft een unieke harmonische "signatuur" voor zijn toon. Houd er rekening mee dat al deze complexiteit betrekking heeft op een enkele noot gespeeld met deze twee 'instrumentstemmen'. Meerdere noten die bijvoorbeeld op een accordeon worden gespeeld, zouden een veel complexere mix van frequenties creëren dan hier te zien is.

De analytische kracht van de oscilloscoop en spectrumanalysator stelt ons in staat om algemene regels over golfvormen en hun harmonische spectra af te leiden uit echte golfvormvoorbeelden. We weten al dat elke afwijking van een zuivere sinusgolf resulteert in het equivalent van een mengsel van meerdere sinusgolfvormen met verschillende amplitudes en frequenties.

Door nauwkeurige observatie kunnen we echter specifieker zijn dan dit. Let bijvoorbeeld op de tijd- en frequentiedomeinplots voor een golfvorm die een blokgolf benadert:

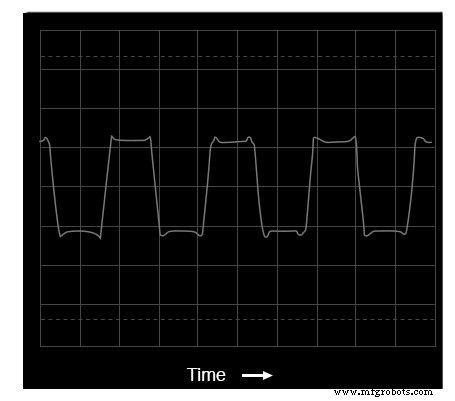
Oscilloscoop tijd-domein weergave van een blokgolf

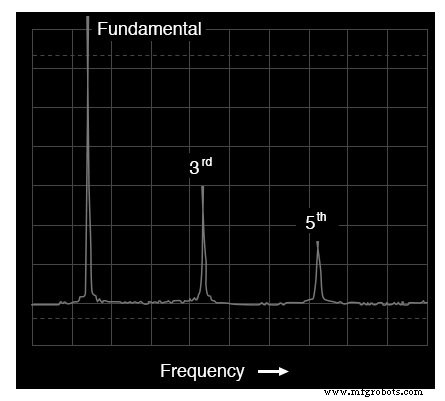
Spectrum (frequentiedomein) van een blokgolf

Volgens de spectrumanalyse bevat deze golfvorm geen even harmonischen, alleen oneven. Hoewel dit scherm geen frequenties na de zesde harmonische weergeeft, gaat het patroon van alleen oneven harmonischen in dalende amplitude oneindig door.

Dit zou geen verrassing moeten zijn, want we hebben al gezien met SPICE dat een blokgolf bestaat uit een oneindig aantal oneven harmonischen. De trompet- en accordeontonen bevatten echter beide even en oneven harmonischen.

Dit verschil in harmonische inhoud is opmerkelijk. Laten we ons onderzoek voortzetten met een analyse van een driehoeksgolf:

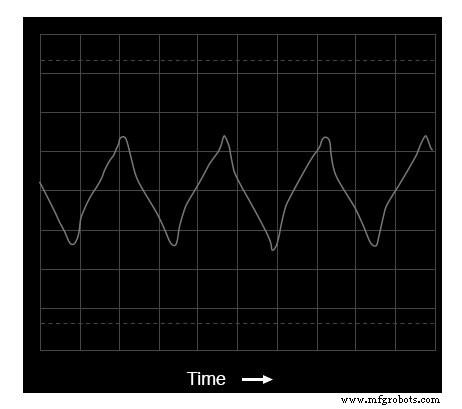
Oscilloscoop tijd-domein weergave van een driehoekige golf

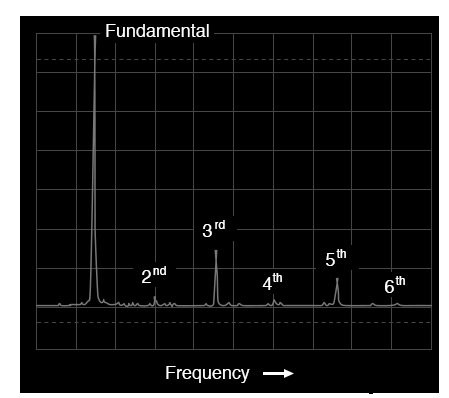
Spectrum van een driehoeksgolf

In deze golfvorm zijn er praktisch geen even harmonischen:(Figuur hierboven) de enige significante frequentiepieken op het spectrumanalysatorscherm behoren tot oneven veelvouden van de grondfrequentie.

Er zijn kleine pieken te zien voor de tweede, vierde en zesde harmonischen, maar dit komt door onvolkomenheden in deze specifieke driehoeksgolfvorm (nogmaals, artefacten van de testapparatuur die in deze analyse is gebruikt).

Een perfecte driehoekige golfvorm produceert geen even harmonischen, net als een perfecte blokgolf. Bij inspectie zou het duidelijk moeten zijn dat het harmonische spectrum van de driehoeksgolf niet identiek is aan het spectrum van de blokgolf:de respectieve harmonische pieken zijn van verschillende hoogte. De twee verschillende golfvormen komen echter vaak voor in hun gebrek aan gelijkmatige harmonischen.

Laten we een andere golfvorm onderzoeken, deze lijkt erg op de driehoeksgolf, behalve dat de stijgtijd niet hetzelfde is als de valtijd. Bekend als een zaagtandgolf , onthult de oscilloscoopplot dat het de toepasselijke naam heeft:

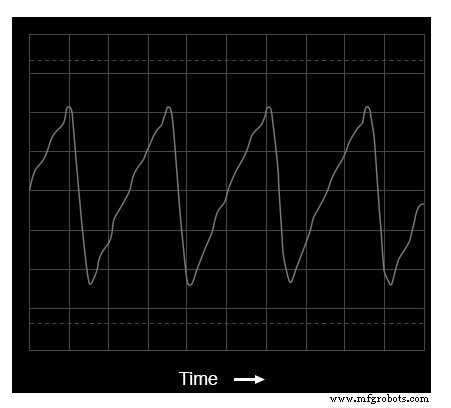
Tijddomeinweergave van een zaagtandgolf

Wanneer de spectrumanalyse van deze golfvorm wordt uitgezet, zien we een resultaat dat heel anders is dan dat van de reguliere driehoeksgolf, want deze analyse toont de sterke aanwezigheid van even genummerde harmonischen (tweede en vierde):

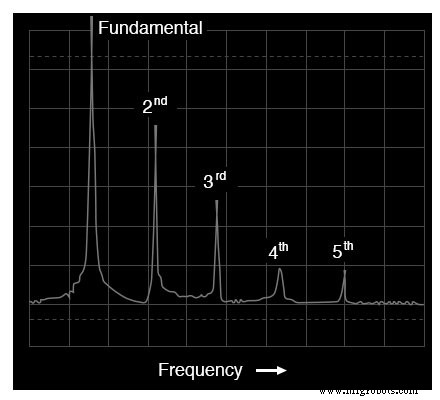
Frequentiedomeinweergave van een zaagtandgolf

Het onderscheid tussen een golfvorm met even harmonischen versus geen even harmonischen zit in het verschil tussen een driehoekige golfvorm en een zaagtandgolfvorm.

Dat verschil is symmetrie boven en onder de horizontale middellijn van de golf. Een golfvorm die symmetrisch is boven en onder de middellijn (de vorm aan beide zijden spiegelt elkaar precies) zal nee bevatten even genummerde harmonischen.

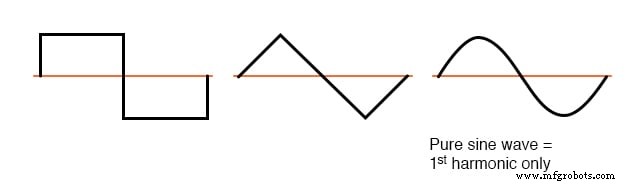
Golfvormen die symmetrisch zijn rond hun x-as middellijn bevatten alleen oneven harmonischen

Vierkante golven, driehoeksgolven en zuivere sinusgolven vertonen allemaal deze symmetrie, en ze zijn allemaal verstoken van zelfs harmonischen. Golfvormen zoals de trompettoon, de accordeontoon en de zaagtandgolf zijn asymmetrisch rond hun middellijnen en daarom doen zelfs harmonischen bevatten.

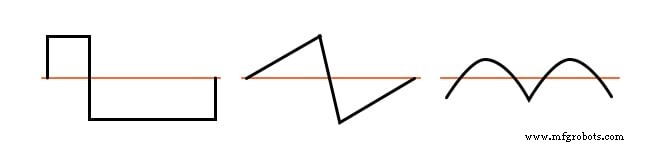
Asymmetrische golfvormen bevatten even harmonischen

Dit principe van middellijnsymmetrie moet niet worden verward met symmetrie rond de nul lijn. In de getoonde voorbeelden is de horizontale middellijn van de golfvorm toevallig nul volt in de tijddomeingrafiek, maar dit heeft niets te maken met harmonische inhoud.

Deze regel van harmonische inhoud (zelfs harmonischen alleen met asymmetrische golfvormen) is van toepassing, ongeacht of de golfvorm boven of onder nul volt wordt verschoven met een "DC-component". Voor verdere verduidelijking zal ik dezelfde reeksen golfvormen laten zien, verschoven met gelijkspanning, en merk op dat hun harmonische inhoud ongewijzigd is.

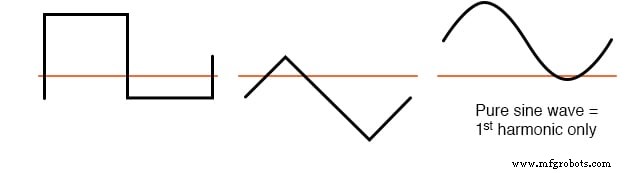
Deze golfvormen bestaan ​​uitsluitend uit oneven harmonischen

Nogmaals, de hoeveelheid gelijkspanning die aanwezig is in een golfvorm heeft niets te maken met de harmonische frequentie-inhoud van die golfvorm.

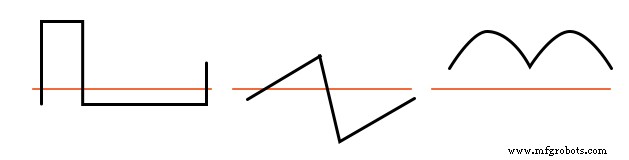
Deze golfvormen bevatten even harmonischen

Waarom is deze harmonische vuistregel een belangrijke regel om te weten? Het kan ons helpen de relatie tussen harmonischen in AC-circuits en specifieke circuitcomponenten te begrijpen.

Aangezien de meeste bronnen van sinusgolfvervorming in wisselstroomcircuits de neiging hebben symmetrisch te zijn, worden even harmonischen zelden gezien in die toepassingen.

Dit is goed om te weten als je een ontwerper van energiesystemen bent en vooruit plant voor harmonische reductie:je hoeft je alleen maar bezig te houden met het verminderen van de oneven harmonische frequenties, zelfs harmonischen zijn praktisch onbestaande.

Als je toevallig zelfs harmonischen in een wisselstroomcircuit meet met een spectrumanalysator of frequentiemeter, weet je dat iets in dat circuit asymmetrisch moet zijn vervorming van de sinusgolfspanning of -stroom, en die aanwijzing kan nuttig zijn bij het lokaliseren van de oorzaak van een probleem (zoek naar componenten of omstandigheden die meer kans hebben om de ene halve cyclus van de AC-golfvorm meer te vervormen dan de andere).

Nu we deze regel hebben om onze interpretatie van niet-sinusvormige golfvormen te sturen, is het logischer dat een golfvorm zoals die geproduceerd door een gelijkrichterschakeling zulke sterke gelijkmatige harmonischen zou moeten bevatten, dat er helemaal geen symmetrie is boven en onder het midden.

BEOORDELING:

• Golfvormen die symmetrisch zijn boven en onder hun horizontale middellijnen bevatten geen even genummerde harmonischen.
• De hoeveelheid aanwezige DC "bias"-spanning (de "DC-component" van een golfvorm) heeft geen invloed op de harmonische frequentie-inhoud van die golf.

GERELATEERDE WERKBLAD:

• Werkblad basisbediening oscilloscoop
• Werkblad passieve integrator- en differentiatorcircuits