Kirchhoff's Voltage Law (KVL)
Wat is de spanningswet van Kirchhoff (KVL)?
Het principe dat bekend staat als Kirchhoff's Spanningswet (ontdekt in 1847 door Gustav R. Kirchhoff, een Duitse natuurkundige) kan als volgt worden gesteld:
“De algebraïsche som van alle spanningen in een lus moet gelijk zijn aan nul”
Door algebraïsch , ik bedoel rekening houdend met zowel tekens (polariteiten) als grootheden. Door lus , ik bedoel elk pad dat is getraceerd van het ene punt in een circuit naar andere punten in dat circuit en uiteindelijk terug naar het beginpunt.
Demonstratie van de spanningswet van Kirchhoff in een serieschakeling
Laten we nog eens kijken naar ons voorbeeldseriecircuit, dit keer door de punten in het circuit te nummeren voor spanningsreferentie:
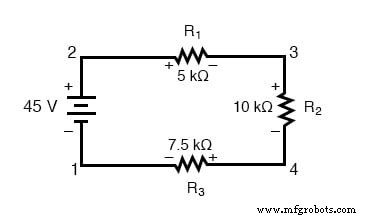
Als we een voltmeter tussen punt 2 en 1 zouden aansluiten, zou het rode meetsnoer op punt 2 en het zwarte meetsnoer op punt 1 staan, dan zou de meter +45 volt registreren. Meestal wordt het "+"-teken niet weergegeven, maar eerder geïmpliceerd, voor positieve metingen in digitale meterdisplays. Voor deze les is de polariteit van de spanningsmeting echter erg belangrijk en daarom zal ik positieve getallen expliciet laten zien:
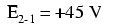
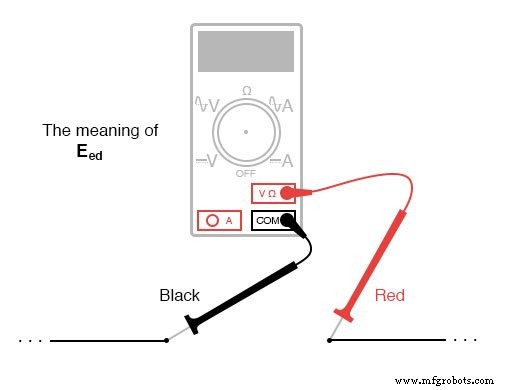
Wanneer een spanning wordt gespecificeerd met een dubbel subscript (de tekens "2-1" in de notatie "E2-1 ”), betekent dit de spanning op het eerste punt (2) zoals gemeten met betrekking tot het tweede punt (1). Een spanning gespecificeerd als "Ecd " zou de spanning betekenen zoals aangegeven door een digitale meter met het rode meetsnoer op punt "c" en het zwarte meetsnoer op punt "d":de spanning op "c" met betrekking tot "d".
Als we dezelfde voltmeter zouden nemen en de spanningsval over elke weerstand zouden meten, met de klok mee rond het circuit stappend met het rode meetsnoer van onze meter op het punt voor ons en het zwarte meetsnoer op het punt erachter, zouden we verkrijgen de volgende metingen:
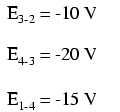
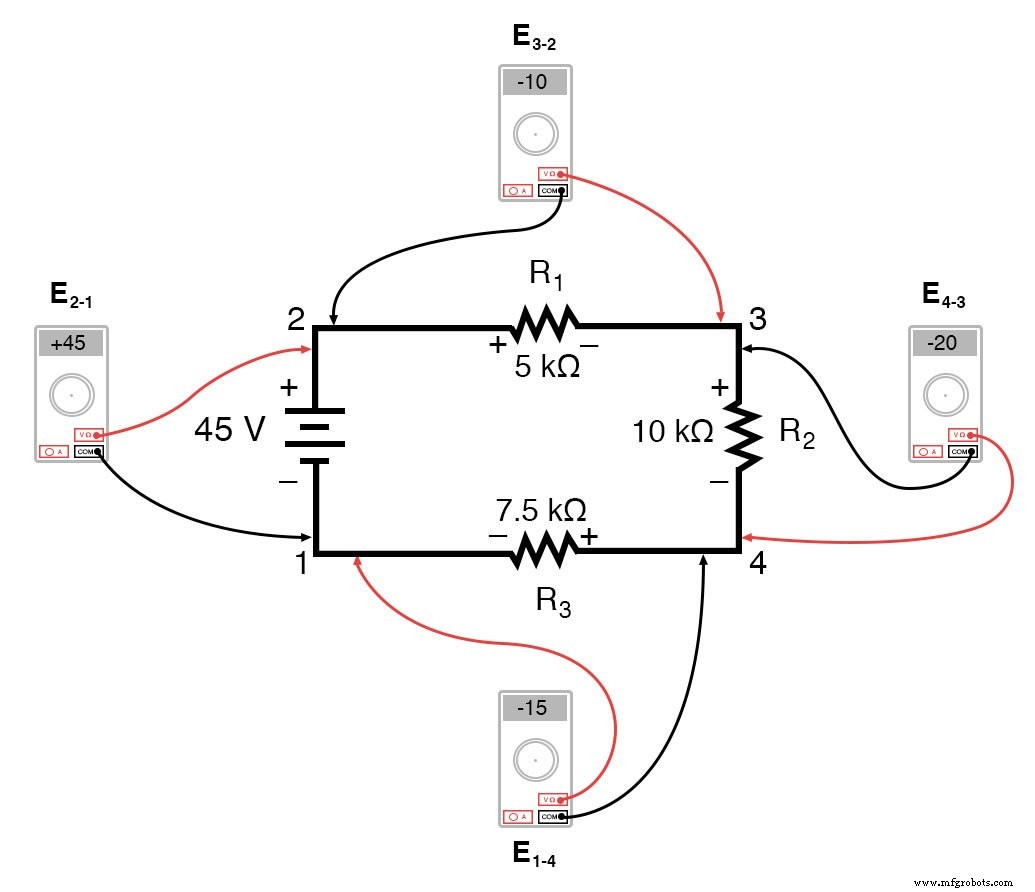
We zouden al bekend moeten zijn met het algemene principe voor serieschakelingen dat individuele spanningsdalingen optellen tot de totale aangelegde spanning, maar het op deze manier meten van spanningsdalingen en aandacht voor de polariteit (wiskundig teken) van de metingen onthult een ander facet hiervan principe:dat de als zodanig gemeten spanningen allemaal optellen tot nul:
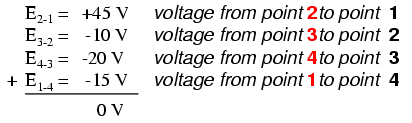
In het bovenstaande voorbeeld werd de lus gevormd door de volgende punten in deze volgorde:1-2-3-4-1. Het maakt niet uit op welk punt we beginnen of in welke richting we doorgaan met het volgen van de lus; de spanningssom zal nog steeds gelijk zijn aan nul. Om te demonstreren, kunnen we de spanningen in lus 3-2-1-4-3 van hetzelfde circuit optellen:
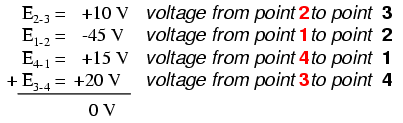
Dit kan logischer zijn als we ons voorbeeldreekscircuit opnieuw tekenen, zodat alle componenten in een rechte lijn worden weergegeven:
Het is nog steeds dezelfde serieschakeling, alleen met de componenten in een andere vorm. Let op de polariteiten van de weerstandsspanningsdalingen ten opzichte van de batterij:de batterijspanning is links negatief en rechts positief, terwijl alle weerstandsspanningsdalingen de andere kant op zijn gericht:positief links en negatief rechts. Dit komt omdat de weerstanden verzetten tegen de stroom van elektrische lading die door de batterij wordt geduwd. Met andere woorden, de "push" die wordt uitgeoefend door de weerstanden tegen de stroom van elektrische lading moet in een richting tegenover de bron van elektromotorische kracht zijn.
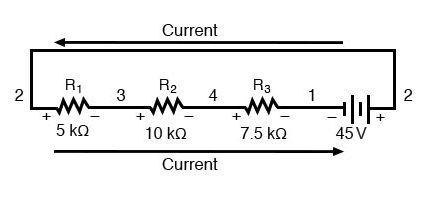
Hier zien we wat een digitale voltmeter zou aangeven over elk onderdeel in dit circuit, de zwarte draad aan de linkerkant en de rode draad aan de rechterkant, zoals horizontaal uitgelegd:
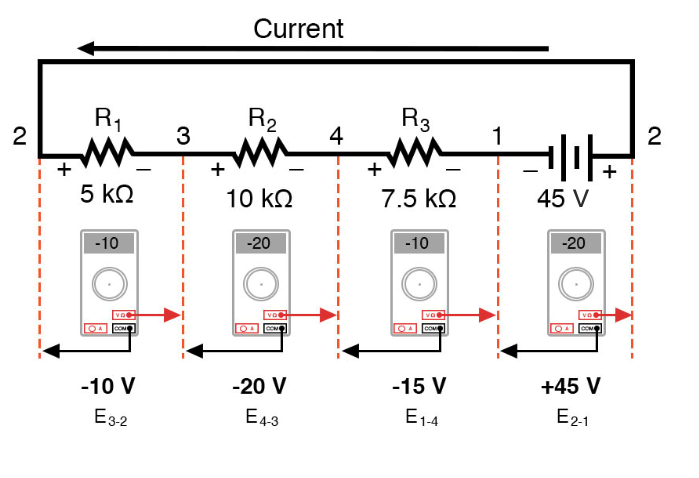
Als we dezelfde voltmeter zouden nemen en de spanning over combinaties van componenten zouden aflezen, te beginnen met de enige R1 aan de linkerkant en vordert over de hele reeks componenten, we zullen zien hoe de spanningen algebraïsch optellen (tot nul):
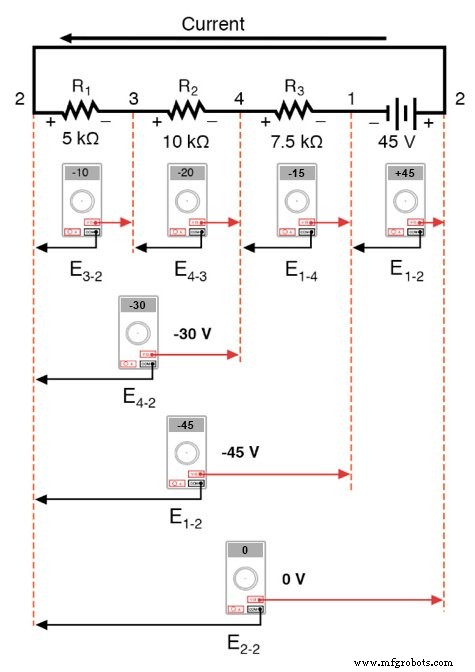
Het feit dat seriespanningen optellen mag geen mysterie zijn, maar we merken dat de polariteit van deze spanningen maakt veel verschil in hoe de cijfers optellen. Tijdens het lezen van spanning over R1 —R2 , en R1 —R2 —R3 (Ik gebruik een "dubbel streepje"-symbool "-" om de reeks weer te geven verbinding tussen weerstanden R1 , R2 , en R3 ), zien we hoe de spanningen achtereenvolgens grotere (zij het negatieve) grootheden meten, omdat de polariteiten van de afzonderlijke spanningsvallen in dezelfde richting staan (positief links, negatief rechts).
De som van de spanningsdalingen over R1 , R2 , en R3 is gelijk aan 45 volt, wat hetzelfde is als de output van de batterij, behalve dat de polariteit van de batterij tegengesteld is aan die van de spanningsdalingen van de weerstand (negatief links, positief rechts), dus we eindigen met 0 volt gemeten over de hele reeks componenten.
Dat we precies 0 volt over de hele snaar zouden moeten krijgen, zou ook geen mysterie moeten zijn. Als we naar het circuit kijken, kunnen we zien dat uiterst links van de snaar (linkerkant van R1 :punt nummer 2) is rechtstreeks verbonden met de uiterst rechtse kant van de snaar (rechterkant van de batterij:punt nummer 2), indien nodig om het circuit te voltooien.
Aangezien deze twee punten direct met elkaar verbonden zijn, zijn ze elektrisch gemeenschappelijk naar elkaar. En als zodanig moet de spanning tussen die twee elektrisch gemeenschappelijke punten moeten nul zijn.
Demonstreren van de spanningswet van Kirchhoff in een parallel circuit
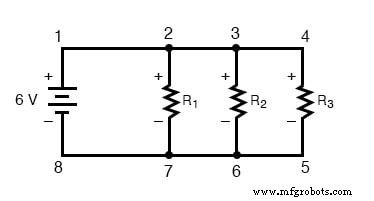
De spanningswet van Kirchhoff (soms aangeduid als KVL in het kort) werkt voor elke circuitconfiguratie helemaal niet, niet alleen eenvoudige series. Merk op hoe het werkt voor deze parallelle schakeling:
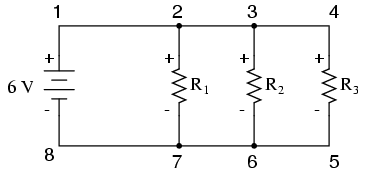
Omdat het een parallelschakeling is, is de spanning over elke weerstand hetzelfde als de voedingsspanning:6 volt. Als we de spanningen rond lus 2-3-4-5-6-7-2 optellen, krijgen we:
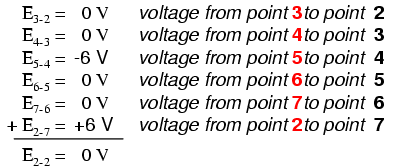
Merk op hoe ik de uiteindelijke (som) spanning label als E2-2 . Aangezien we onze loop-stapreeks bij punt 2 begonnen en eindigden bij punt 2, zal de algebraïsche som van die spanningen hetzelfde zijn als de spanning gemeten tussen hetzelfde punt (E2-2 ), wat natuurlijk nul moet zijn.
De geldigheid van de spanningswet van Kirchhoff, ongeacht de circuittopologie
Het feit dat dit circuit parallel is in plaats van serie heeft niets te maken met de geldigheid van de spanningswet van Kirchhoff. Overigens zou het circuit een "zwarte doos" kunnen zijn - de configuratie van de componenten is volledig aan ons zicht onttrokken, met alleen een set blootgestelde terminals voor ons om de spanning tussen te meten - en KVL zou nog steeds gelden:
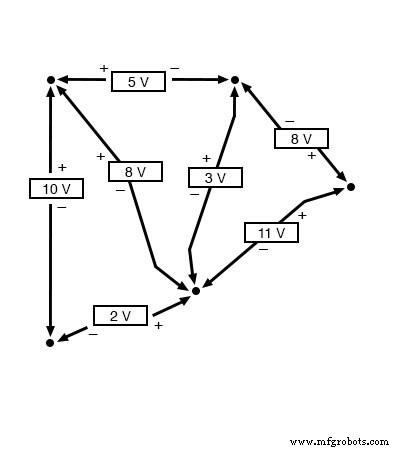
Probeer een willekeurige volgorde van stappen vanaf elke terminal in het bovenstaande diagram, stap terug naar de originele terminal, en je zult zien dat de algebraïsche som van de spanningen altijd is gelijk aan nul.
Bovendien hoeft de "lus" die we voor KVL volgen niet eens een echt stroompad te zijn in de gesloten zin van het woord. Het enige dat we hoeven te doen om aan KVL te voldoen, is om op hetzelfde punt in het circuit te beginnen en te eindigen, waarbij we spanningsdalingen en polariteiten optellen terwijl we tussen het volgende en het laatste punt gaan. Beschouw dit absurde voorbeeld, het traceren van "lus" 2-3-6-3-2 in hetzelfde parallelle weerstandscircuit:
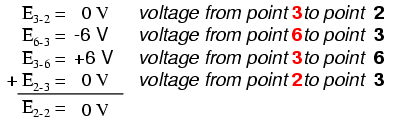
De spanningswet van Kirchhoff gebruiken in een complex circuit
KVL kan worden gebruikt om een onbekende spanning te bepalen in een complexe schakeling, waar alle andere spanningen rond een bepaalde "lus" bekend zijn. Neem de volgende complexe schakeling (eigenlijk twee serieschakelingen verbonden door een enkele draad aan de onderkant) als voorbeeld:
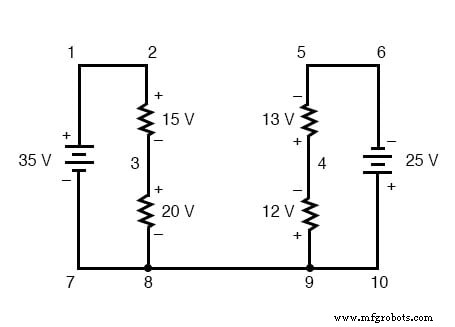
Om het probleem eenvoudiger te maken, heb ik weerstandswaarden weggelaten en eenvoudigweg spanningsdalingen over elke weerstand gegeven. De twee serieschakelingen delen een gemeenschappelijke draad tussen hen (draad 7-8-9-10), waardoor spanningsmetingen tussen de twee circuits mogelijk. Als we de spanning tussen de punten 4 en 3 wilden bepalen, zouden we een KVL-vergelijking kunnen opstellen met de spanning tussen die punten als de onbekende:
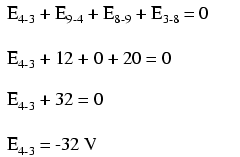
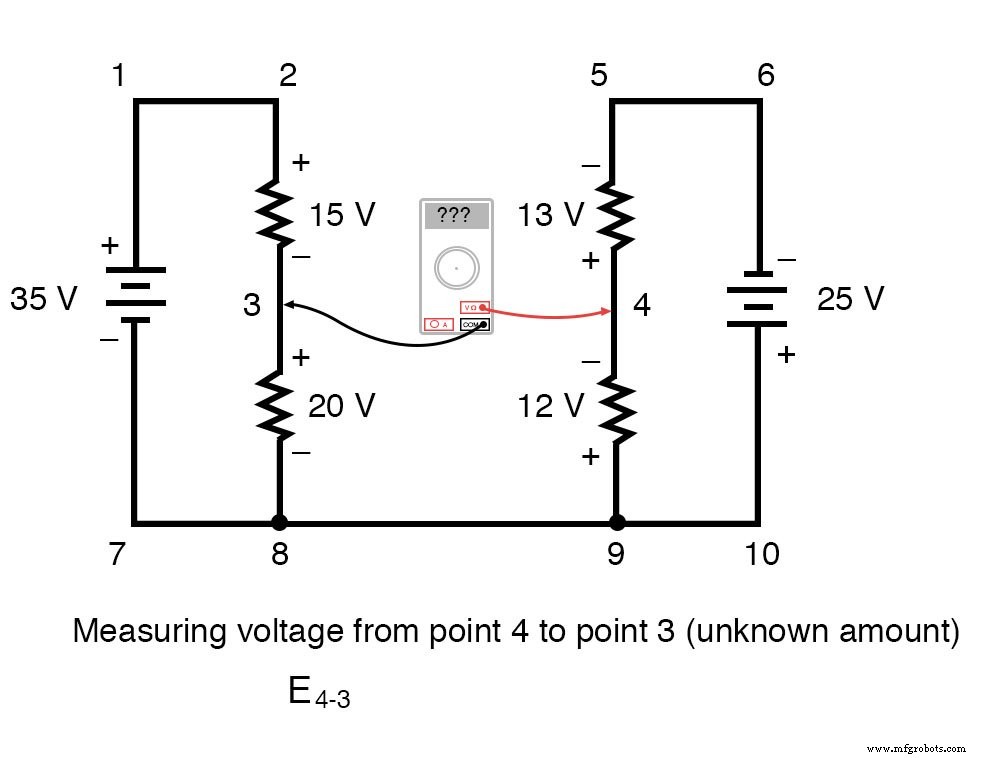
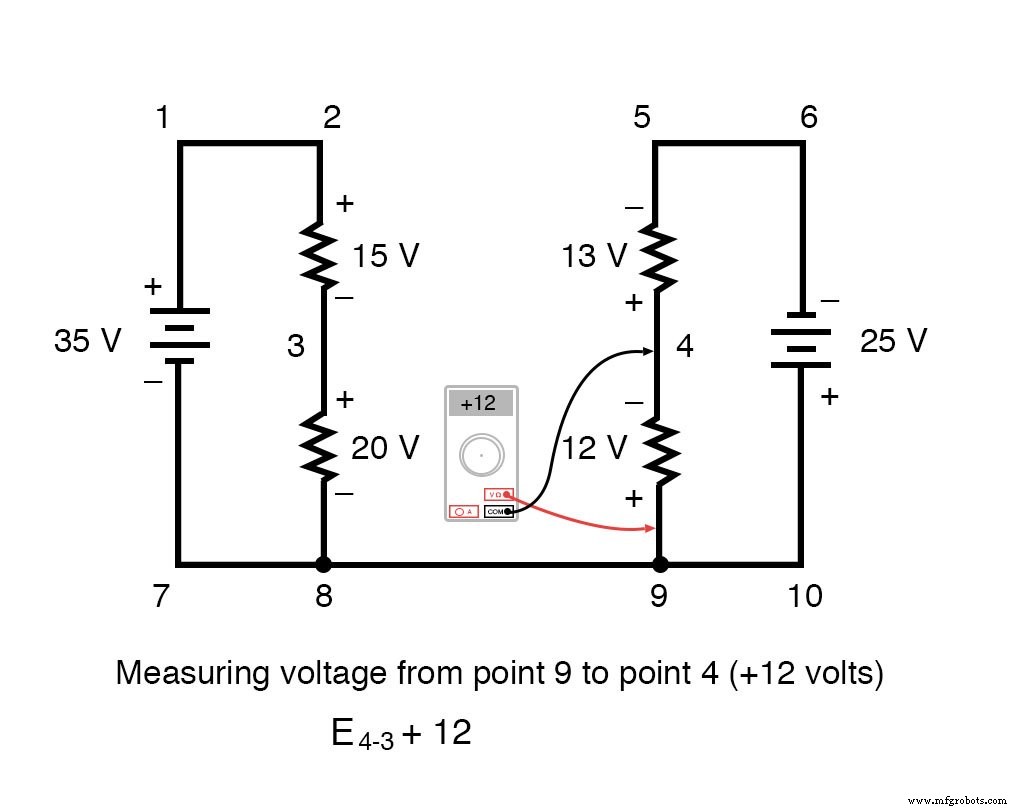
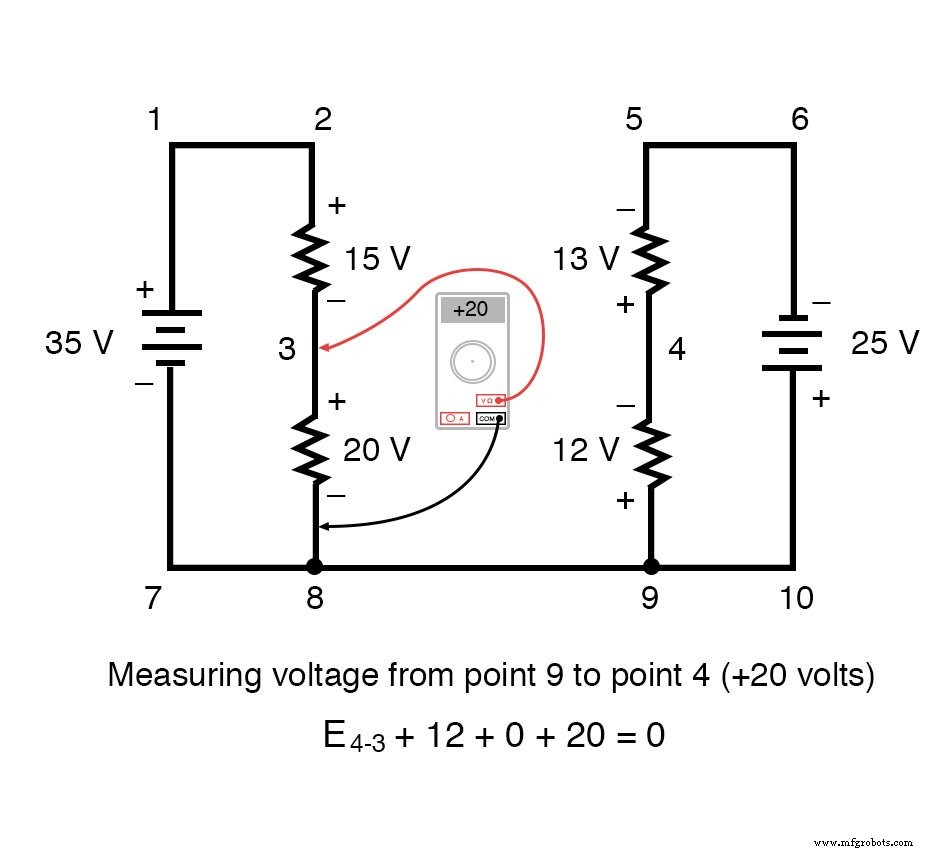
Stappen rond de lus 3-4-9-8-3, we schrijven de spanningsdalingscijfers zoals een digitale voltmeter ze zou registreren, meten met het rode meetsnoer op het punt voor ons en het zwarte meetsnoer op het punt erachter terwijl we verder gaan de lus. Daarom is de spanning van punt 9 naar punt 4 een positieve (+) 12 volt omdat de "rode draad" op punt 9 staat en de "zwarte draad" op punt 4.
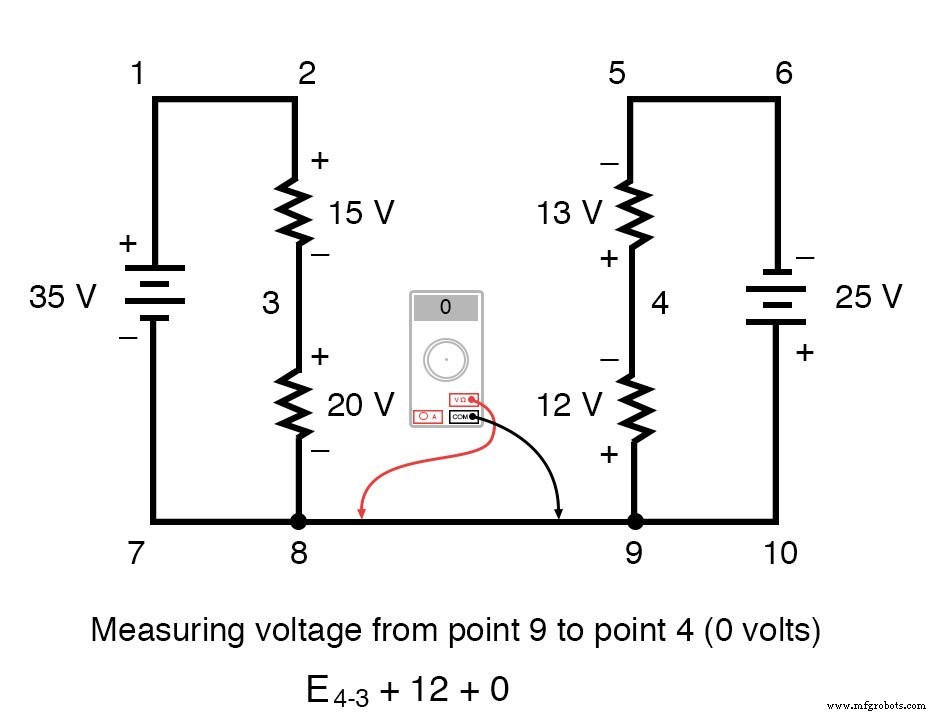
De spanning van punt 3 naar punt 8 is een positieve (+) 20 volt omdat de "rode draad" op punt 3 zit en de "zwarte draad" op punt 8. De spanning van punt 8 naar punt 9 is natuurlijk nul , omdat die twee punten elektrisch gemeenschappelijk zijn.
Ons laatste antwoord voor de spanning van punt 4 naar punt 3 is een negatieve (-) 32 volt, wat ons vertelt dat punt 3 eigenlijk positief is met betrekking tot punt 4, precies wat een digitale voltmeter zou aangeven met de rode draad op punt 4 en de zwarte draad op punt 3:
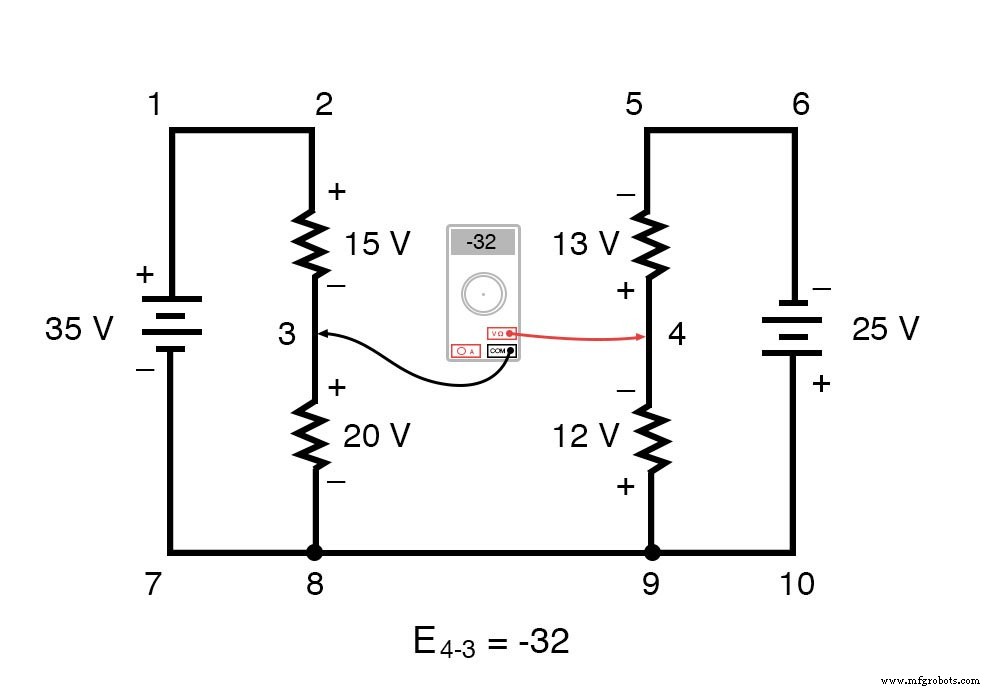
Met andere woorden, de initiële plaatsing van onze "meterkabels" in dit KVL-probleem was "achterwaarts". Hadden we onze KVL-vergelijking gegenereerd, beginnend met E3-4 in plaats van E4-3 , door dezelfde lus te stappen met de tegenovergestelde richting van de meter, zou het uiteindelijke antwoord E3-4 zijn geweest =+32 volt:
Het is belangrijk om te beseffen dat geen van beide benaderingen "fout" is. In beide gevallen komen we tot de juiste beoordeling van de spanning tussen de twee punten 3 en 4:punt 3 is positief ten opzichte van punt 4 en de spanning daartussen is 32 volt.
BEOORDELING:
- Kirchhoff's spanningswet (KVL):"De algebraïsche som van alle spanningen in een lus moet gelijk zijn aan nul"
GERELATEERDE WERKBLAD:
- Wetten werkblad van Kirchhoff
Industriële technologie



