Finite State Machines

Tot nu toe was elk circuit dat werd gepresenteerd een combinatie stroomkring. Dat betekent dat de output alleen afhankelijk is van de huidige inputs. Eerdere inputs voor dat type circuits hebben geen effect op de output.

Er zijn echter veel toepassingen waarbij onze circuits "geheugen" moeten hebben; om eerdere invoer te onthouden en hun uitvoer op basis daarvan te berekenen. Een circuit waarvan de uitvoer niet alleen afhangt van de huidige invoer, maar ook van de geschiedenis van de invoer, wordt een sequentieel circuit genoemd. .

In deze sectie zullen we leren hoe we dergelijke sequentiële circuits kunnen ontwerpen en bouwen. Om te zien hoe deze procedure werkt, zullen we een voorbeeld gebruiken, waarop we ons onderwerp zullen bestuderen.

Dus laten we aannemen dat we een digitaal quizspel hebben dat werkt op een klok en een invoer leest van een handmatige knop. We willen echter dat de schakelaar slechts één HOGE puls naar het circuit verzendt. Als we de knop rechtstreeks op het spelcircuit haken, zendt deze HOOG uit voor zo weinig klokcycli als onze vinger kan bereiken. Op een gewone klokfrequentie kan onze vinger nooit snel genoeg zijn.

De ontwerpprocedure heeft specifieke stappen die moeten worden gevolgd om het werk gedaan te krijgen:

Stap 1

De eerste stap van de ontwerpprocedure is om met eenvoudige maar duidelijke woorden te definiëren wat we willen dat onze schakeling doet:

"Onze missie is om een ​​secundair circuit te ontwerpen dat een HOGE puls uitzendt met een duur van slechts één cyclus wanneer de handmatige knop wordt ingedrukt, en geen nieuwe puls uitzendt totdat de knop wordt ingedrukt en opnieuw wordt ingedrukt." em>

Stap 2

De volgende stap is het ontwerpen van een toestandsdiagram.

Dit is een diagram dat is gemaakt van cirkels en pijlen en dat visueel de werking van ons circuit beschrijft. In wiskundige termen is dit diagram dat de werking van ons sequentiële circuit beschrijft een eindige toestandsmachine. Noteer dat dit een Moore Finite State Machine is.

De uitvoer is alleen een functie van de huidige staat, niet de invoer. Dat in tegenstelling tot de Mealy Finite State Machine, waar input de output beïnvloedt. In deze tutorial wordt alleen de Moore Finite State Machine onderzocht.

Het toestandsdiagram van ons circuit is het volgende:(figuur hieronder)

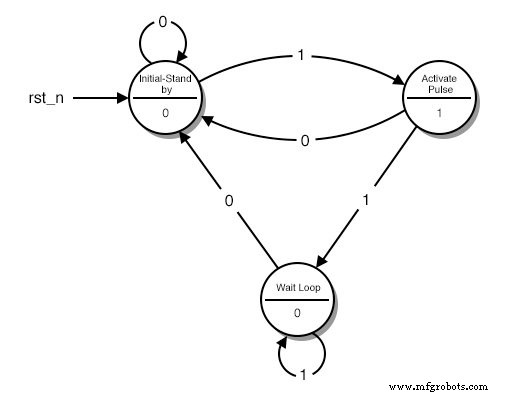
Een toestandsdiagram

Elke cirkel vertegenwoordigt een "staat", een goed gedefinieerde toestand waarin onze machine te vinden is. In de bovenste helft van de cirkel beschrijven we die toestand. De beschrijving helpt ons herinneren wat ons circuit in die toestand zou moeten doen.

• De eerste cirkel is de stand-by-toestand. Dit is waar ons circuit begint en waar het wacht op nog een druk op de knop.
• De tweede cirkel is de toestand waarbij de knop zojuist is ingedrukt en ons circuit een HOGE puls moet verzenden.
• De derde cirkel is de toestand waarin ons circuit wacht tot de knop wordt losgelaten voordat het terugkeert naar de "stand-by" toestand.

In het onderste deel van de cirkel is de output van ons circuit. Als we willen dat onze schakeling een HIGH uitzendt voor een specifieke toestand, zetten we een 1 op die toestand. Anders zetten we een 0.

Elke pijl vertegenwoordigt een "overgang" van de ene staat naar de andere. Een overgang vindt eenmaal per klokcyclus plaats. Afhankelijk van de huidige Input kunnen we elke keer naar een andere status gaan. Let op het nummer in het midden van elke pijl. Dit is de huidige invoer.

Wanneer we ons bijvoorbeeld in de staat "Initial-Stand by" bevinden en we "lezen" een 1, vertelt het diagram ons dat we naar de staat "Activate Pulse" moeten gaan. Als we een 0 lezen, moeten we in de staat "Initial-Stand by" blijven.

Dus, wat doet onze "Machine" precies? Het begint vanuit de "Initial - Stand by" status en wacht tot er een 1 wordt gelezen bij de ingang. Daarna gaat het naar de status "Activate Pulse" en zendt een HOGE puls op zijn uitgang. Als de knop ingedrukt blijft, gaat het circuit naar de derde status, de "Wachtloop".

Daar wacht het totdat de knop wordt losgelaten (Input gaat 0) terwijl een LOW op de uitgang wordt verzonden. Dan is het allemaal weer voorbij!

Dit is misschien wel het moeilijkste onderdeel van de ontwerpprocedure, omdat het niet in eenvoudige stappen kan worden beschreven. Het vergt ervaring en een beetje scherp denken om een ​​toestandsdiagram op te zetten, maar de rest is slechts een reeks vooraf bepaalde stappen.

Stap 3

Vervolgens vervangen we de woorden die de verschillende toestanden van het diagram beschrijven door binair nummers. We beginnen de opsomming vanaf 0 die is toegewezen aan de beginstatus. We gaan dan door met de telling met elke staat die we willen, totdat alle staten hun nummer hebben. Het resultaat ziet er ongeveer zo uit:(figuur hieronder)

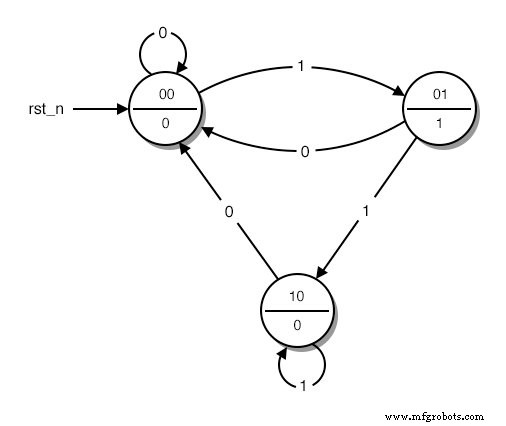
Een toestandsdiagram met gecodeerde toestanden

Stap 4

Daarna vullen we de Statentabel . Deze tabel heeft een heel specifieke vorm. Ik zal de tabel van ons voorbeeld geven en deze gebruiken om uit te leggen hoe deze moet worden ingevuld. (Figuur hieronder)

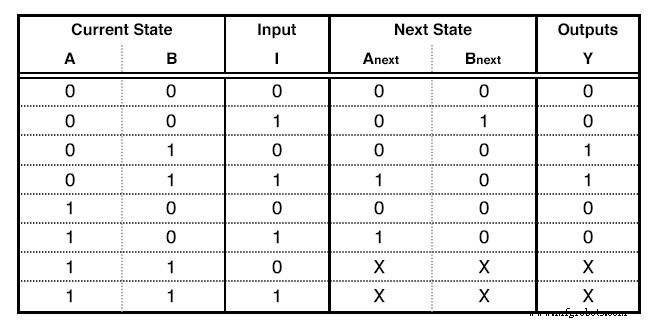
Een statustabel

De eerste kolommen zijn net zoveel als de bits van het hoogste nummer dat we aan het toestandsdiagram hebben toegewezen. Als we 5 staten hadden, zouden we tot het getal 100 hebben gebruikt, wat betekent dat we 3 kolommen zouden gebruiken. Voor ons voorbeeld hebben we tot het getal 10 gebruikt, dus er zijn slechts 2 kolommen nodig. Deze kolommen beschrijven de Huidige staat van ons circuit.

Rechts van de Current State-kolommen schrijven we de Input Columns . Dit zullen er net zoveel zijn als onze invoervariabelen. Ons voorbeeld heeft maar één invoer.

Vervolgens schrijven we de Volgende State Columns . Dit zijn er zoveel als de kolommen Huidige staat.

Ten slotte schrijven we de Uitvoerkolommen . Dit zijn er net zoveel als onze outputs. Ons voorbeeld heeft slechts één uitvoer. Omdat we een meer eindige toestandsmachine hebben gebouwd, is de uitvoer alleen afhankelijk van de huidige invoerstatussen. Dit is de reden dat de outputkolom twee 1 heeft:om te resulteren in een output Booleaanse functie die onafhankelijk is van input I. Lees verder voor meer details. De kolommen Current State en Input zijn de Inputs van onze tabel. We vullen ze in met alle binaire getallen van 0 tot:

2 ^{(Aantal kolommen met huidige status + aantal invoerkolommen)} -1

Het is eenvoudiger dan het klinkt gelukkig. Gewoonlijk zullen er meer rijen zijn dan de werkelijke toestanden die we in het toestandsdiagram hebben gemaakt, maar dat is oké.

Elke rij van de Next State-kolommen is als volgt gevuld:We vullen deze in met de status die we bereiken wanneer we in het Statusdiagram vanuit de Huidige Status van dezelfde rij de invoer van dezelfde rij volgen. Als u een rij moet invullen waarvan het nummer van de huidige staat niet overeenkomt met een werkelijke staat in het staatsdiagram, vullen we deze met de termen Don't Care (X). Het maakt ons tenslotte niet uit waar we heen kunnen gaan vanuit een staat die niet bestaat. We zouden er in de eerste plaats niet zijn! Nogmaals, het is eenvoudiger dan het klinkt.

De outputkolom wordt gevuld door de output van de corresponderende Huidige Staat in het Statusdiagram.

De Staatstabel is compleet! Het beschrijft het gedrag van ons circuit net zo volledig als het toestandsdiagram.

Stap 5a

De volgende stap is om die theoretische "Machine" te nemen en in een circuit te implementeren. Meestal gaat het bij deze implementatie om flip-flops. Deze handleiding is gewijd aan dit soort implementatie en beschrijft de procedure voor zowel D - Flip Flops als JK - Flip Flops. T - Teenslippers worden niet meegeleverd omdat ze te veel op de twee vorige hoesjes lijken. De keuze van de te gebruiken flip-flop is willekeurig en wordt meestal bepaald door kostenfactoren. De beste keuze is om zowel een analyse uit te voeren als te beslissen welk type flip-flop resulteert in een minimaal aantal logische poorten en lagere kosten.

Eerst zullen we onderzoeken hoe we onze "Machine" implementeren met D-Flip Flops.

We hebben net zoveel D - Flip Flops nodig als de State-kolommen, 2 in ons voorbeeld. Voor elke flip-flop voegen we nog een kolom toe aan onze staatstabel (afbeelding hieronder) met de naam van de invoer van de flip-flop, "D" voor dit geval. De kolom die overeenkomt met elke flip-flop beschrijft welke invoer we de flip-flop moeten geven om van de huidige staat naar de volgende staat te gaan . Voor de D - Flip Flop is dit eenvoudig:De benodigde invoer is gelijk aan de Next State. In de rijen die X'en bevatten, vullen we ook X'en in deze kolom.

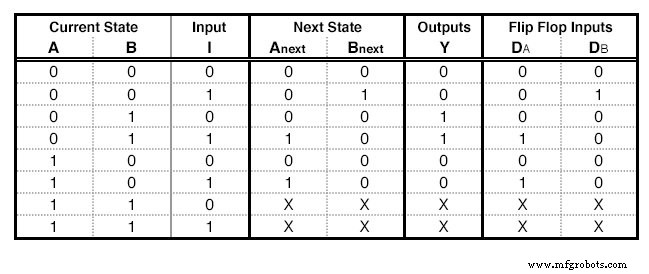
Een toestandstabel met D - Flip Flop-excitaties

Stap 5b

We kunnen dezelfde stappen doen met JK - Flip Flops. Er zijn echter enkele verschillen. Een JK - Flip Flop heeft twee ingangen, daarom moeten we voor elke Flip Flop twee kolommen toevoegen. De inhoud van elke cel wordt bepaald door de excitatietabel van de JK:

Deze tabel zegt dat als we van staat Q naar staat Q willen gaan_volgende , moeten we de specifieke invoer voor elke terminal gebruiken. Om bijvoorbeeld van 0 naar 1 te gaan, moeten we J voeden met 1 en het maakt ons niet uit welke input we naar terminal K voeren.

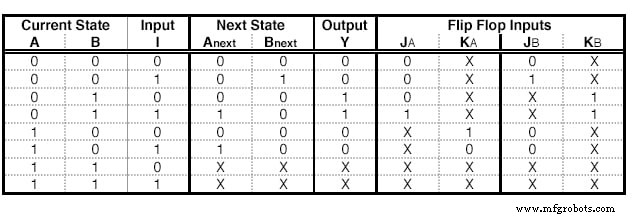
Een toestandstabel met JK - Flip Flop-excitaties

Stap 6

We zitten in de laatste fase van onze procedure. Wat overblijft, is het bepalen van de Booleaanse functies die de invoer van onze flip-flops en de uitvoer produceren. We zullen één Booleaanse functie extraheren voor elke Flip Flop-invoer die we hebben. Dit kan met een Karnaugh-kaart. De invoervariabelen van deze kaart zijn de Current State-variabelen en ook de ingangen.

Dat gezegd hebbende, de invoerfuncties voor onze D - Teenslippers zijn de volgende:(Figuur hieronder)

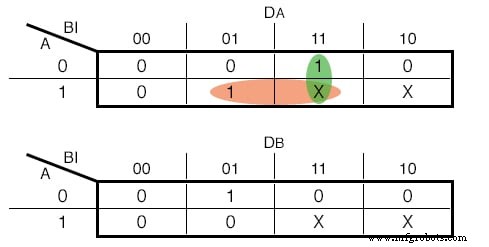
Karnaugh-kaarten voor de D - Flip Flop-ingangen

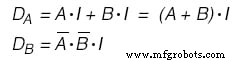
Als we ervoor zouden kiezen om JK - Flip Flops te gebruiken, zouden onze functies de volgende zijn:(Figuur hieronder)

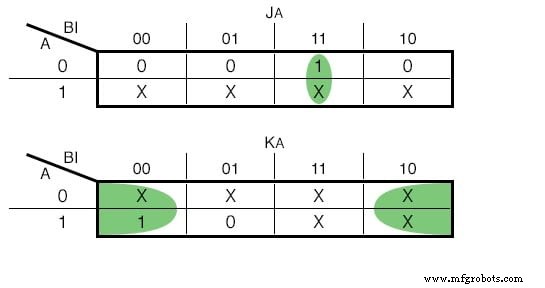
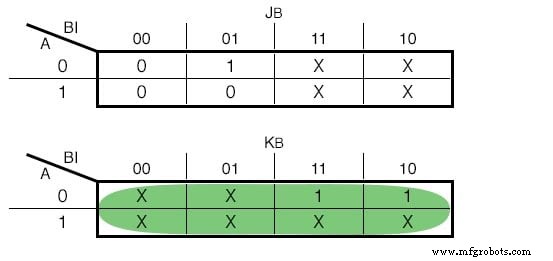
Karnaugh-kaart voor de JK - Flip Flop-invoer

Er wordt ook een Karnaugh-kaart gebruikt om de functie van de uitvoer te bepalen:(figuur hieronder)

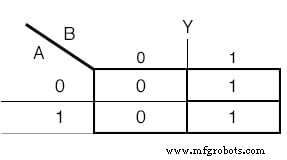
Karnaugh-kaart voor de uitvoervariabele Y

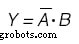
Stap 7

We ontwerpen onze schakeling. We plaatsen de flip-flops en gebruiken logische poorten om de Booleaanse functies te vormen die we hebben berekend. De poorten nemen input van de output van de Flip Flops en de input van het circuit. Vergeet niet de klok aan te sluiten op de teenslippers!

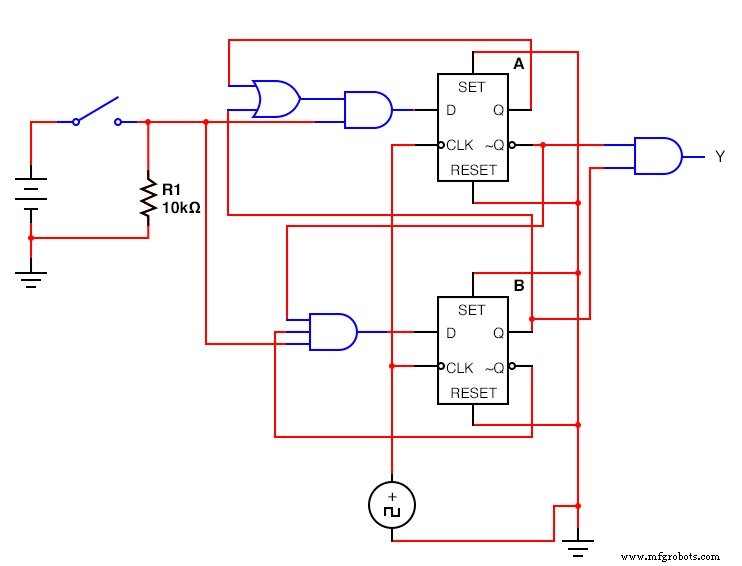
De D - Flip Flop-versie:(afbeelding hieronder)

Het voltooide D - Flip Flop Sequential Circuit

De JK - Flip Flop-versie:(figuur hieronder)

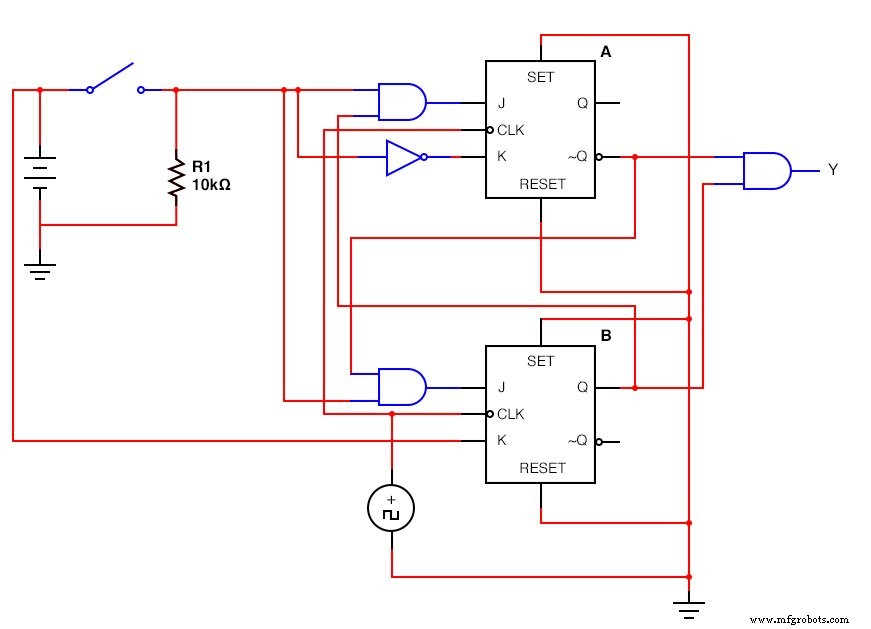
Het voltooide JK - Flip Flop Sequential Circuit

Dit is het! We hebben met succes een sequentieel circuit ontworpen en gebouwd. In eerste instantie lijkt het misschien een ontmoedigende taak, maar na oefening en herhaling zal de procedure triviaal worden. Sequentiële circuits kunnen van pas komen als besturingsonderdelen van grotere circuits en kunnen elke sequentiële logische taak uitvoeren die we maar kunnen bedenken. De lucht is de limiet! (of tenminste de printplaat)

BEOORDELING:

• Een sequentiële logische functie heeft een "geheugen"-functie en houdt rekening met eerdere invoer om te beslissen over de uitvoer.
• De Finite State Machine is een abstract wiskundig model van een sequentiële logische functie. Het heeft eindige inputs, outputs en aantal toestanden.
• FSM's worden geïmplementeerd in real-life circuits door het gebruik van teenslippers
• De implementatieprocedure heeft een specifieke volgorde van stappen (algoritme) nodig om te kunnen worden uitgevoerd.