Lokale minima in neurale netwerktraining begrijpen

In dit artikel wordt een complicatie besproken die kan voorkomen dat uw Perceptron de juiste classificatienauwkeurigheid bereikt.

In de serie neurale netwerken van AAC hebben we een breed scala aan onderwerpen behandeld die te maken hebben met het begrijpen en ontwikkelen van meerlaagse neurale netwerken van Perceptron. Lees voordat u dit artikel over lokale minima leest de rest van de serie hieronder:

1. Hoe classificatie uitvoeren met behulp van een neuraal netwerk:wat is de Perceptron?
2. Een eenvoudig Perceptron neuraal netwerkvoorbeeld gebruiken om gegevens te classificeren
3. Een basis Perceptron neuraal netwerk trainen
4. Eenvoudige neurale netwerktraining begrijpen
5. Een inleiding tot trainingstheorie voor neurale netwerken
6. De leersnelheid in neurale netwerken begrijpen
7. Geavanceerde machine learning met de meerlaagse Perceptron
8. De Sigmoid-activeringsfunctie:activering in meerlaagse Perceptron neurale netwerken
9. Een meerlagig Perceptron neuraal netwerk trainen
10. Trainingsformules en backpropagation voor meerlaagse perceptrons begrijpen
11. Neurale netwerkarchitectuur voor een Python-implementatie
12. Hoe maak je een meerlaags Perceptron neuraal netwerk in Python
13. Signaalverwerking met behulp van neurale netwerken:validatie in neuraal netwerkontwerp
14. Trainingsdatasets voor neurale netwerken:een neuraal netwerk met Python trainen en valideren
15. Hoeveel verborgen lagen en verborgen knooppunten heeft een neuraal netwerk nodig?
16. De nauwkeurigheid van een neuraal netwerk met verborgen lagen vergroten
17. Bias-knooppunten opnemen in uw neurale netwerk
18. Lokale minima in neurale netwerktraining begrijpen

Neural-netwerk training is een complex proces. Gelukkig hoeven we het niet perfect te begrijpen om ervan te profiteren:de netwerkarchitecturen en trainingsprocedures die we gebruiken, resulteren echt in functionele systemen die een zeer hoge classificatienauwkeurigheid bereiken. Er is echter één theoretisch aspect van training dat, ondanks dat het enigszins duister is, onze aandacht verdient.

We noemen het 'het probleem van lokale minima'.

Waarom verdienen lokale minima onze aandacht?

Nou... ik weet het niet zeker. Toen ik voor het eerst hoorde over neurale netwerken, kreeg ik de indruk dat lokale minima echt een belangrijk obstakel zijn voor succesvolle training, tenminste als we te maken hebben met complexe input-outputrelaties. Ik ben echter van mening dat recent onderzoek het belang van lokale minima bagatelliseert. Misschien hebben nieuwere netwerkstructuren en verwerkingstechnieken de ernst van het probleem verminderd, of misschien hebben we gewoon een beter begrip van hoe neurale netwerken daadwerkelijk naar de gewenste oplossing navigeren.

Aan het einde van dit artikel zullen we de huidige status van lokale minima opnieuw bekijken. Voor nu zal ik mijn vraag als volgt beantwoorden:Lokale minima verdienen onze aandacht omdat ze ons ten eerste helpen om dieper na te denken over wat er werkelijk gebeurt als we een netwerk trainen via gradiëntafdaling, en ten tweede omdat lokale minima zijn— of tenminste waren —beschouwd als een significante belemmering voor de succesvolle implementatie van neurale netwerken in real-life systemen.

Wat is een lokaal minimum?

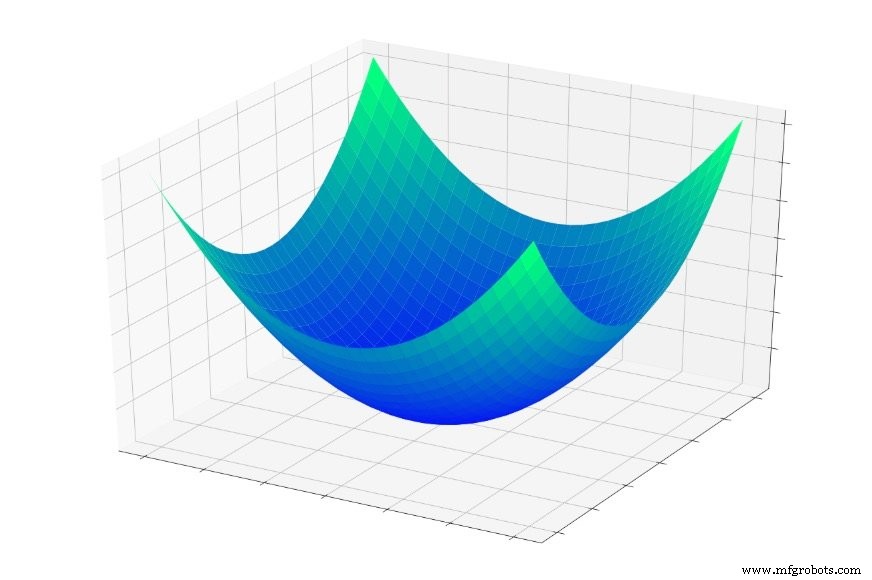
In deel 5 beschouwden we de hieronder getoonde "error bowl", en ik beschreef training als in wezen een zoektocht naar het laagste punt in deze schaal.

(Opmerking :In dit artikel zullen mijn afbeeldingen en uitleg vertrouwen op ons intuïtieve begrip van driedimensionale structuren, maar onthoud dat de algemene concepten niet beperkt zijn tot driedimensionale relaties. We gebruiken inderdaad vaak neurale netwerken waarvan de dimensionaliteit veel groter is dan twee invoervariabelen en één uitvoervariabele.)

Als je in deze schaal zou springen, zou je elke keer naar de bodem glijden. Het maakt niet uit waar je begint , beland je op het laagste punt van de hele foutfunctie. Dit laagste punt is het algemene minimum . Wanneer een netwerk is geconvergeerd op het wereldwijde minimum, heeft het zijn vermogen om de trainingsgegevens te classificeren geoptimaliseerd, en in theorie , dit is het fundamentele doel van training:doorgaan met het aanpassen van gewichten totdat het globale minimum is bereikt.

We weten echter dat neurale netwerken in staat zijn om extreem complexe input-outputrelaties te benaderen. De bovenstaande foutkom past niet precies in de categorie "extreem complex". Het is gewoon een plot van de functie \(f(x,y) =x^2 + y^2\).

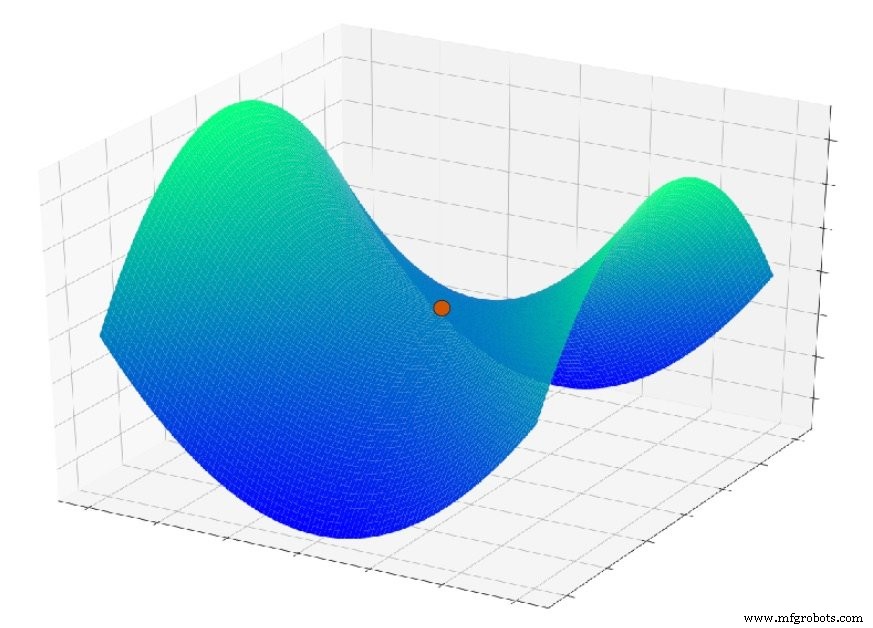
Maar stel je nu voor dat de foutfunctie er ongeveer zo uitziet:

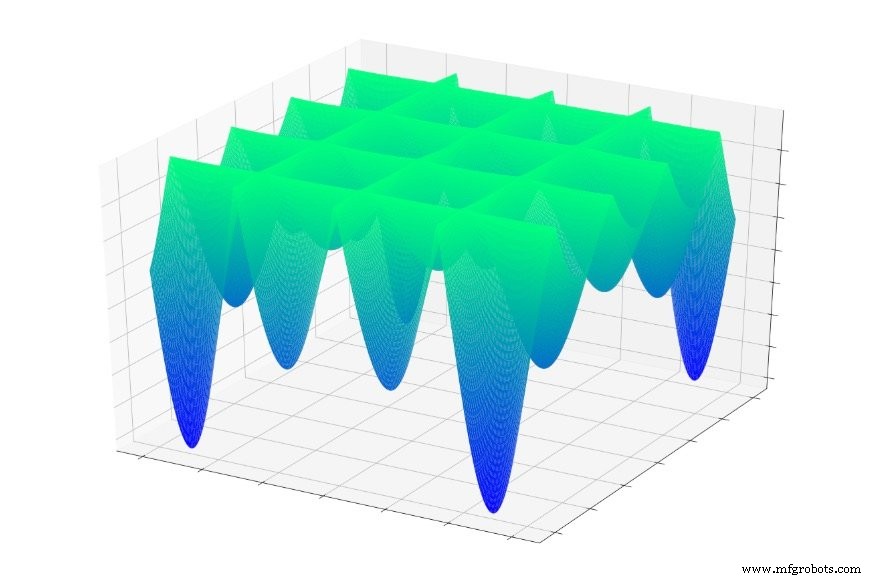
Of dit:

Of dit:

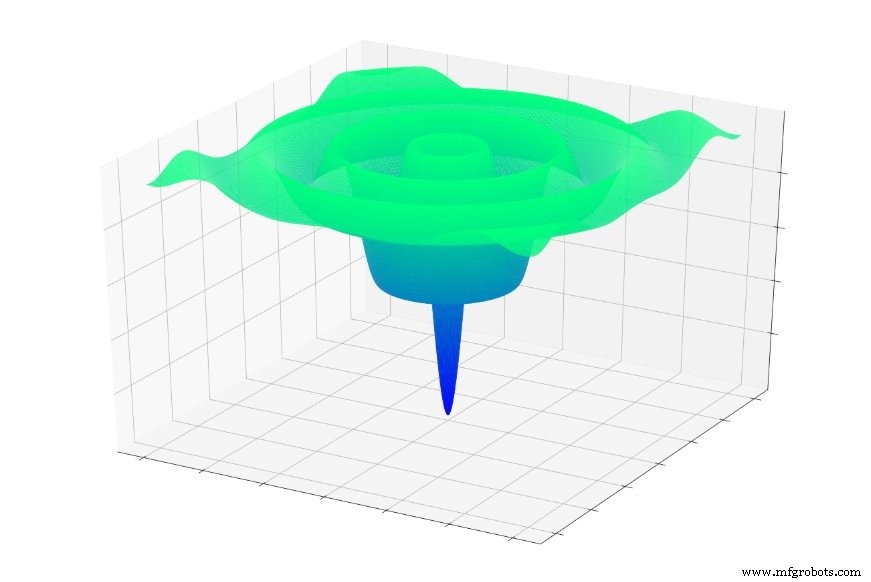
Als je willekeurig in een van deze functies zou springen, zou je vaak naar een lokaal minimum glijden. U bevindt zich dan op het laagste punt van een gelokaliseerd deel van de grafiek, maar u bent misschien niet in de buurt van de algemene minimaal.

Hetzelfde kan gebeuren met een neuraal netwerk. Gradiëntafdaling is afhankelijk van lokaal informatie die, naar we hopen, een netwerk zal leiden naar de wereldwijde minimum. Het netwerk heeft geen voorkennis over de kenmerken van het totale foutoppervlak, en bijgevolg wanneer het een punt bereikt dat lijkt op de onderkant van het foutoppervlak op basis van lokale informatie , kan het geen topografische kaart tevoorschijn halen en bepalen dat het terug bergopwaarts moet om het punt te vinden dat eigenlijk lager is dan alle andere.

Wanneer we een basisgradiëntafdaling implementeren, vertellen we het netwerk:"Zoek de onderkant van een foutoppervlak en blijf daar." We zeggen niet:"Zoek de onderkant van een foutoppervlak, noteer je coördinaten en blijf dan bergop en neer wandelen totdat je de volgende vindt. Laat het me weten als je klaar bent.'

Willen we echt het wereldwijde minimum vinden?

Het is redelijk om aan te nemen dat het globale minimum de optimale oplossing vertegenwoordigt, en om te concluderen dat lokale minima problematisch zijn omdat training zou kunnen "vastlopen" in een lokaal minimum in plaats van door te gaan naar het globale minimum.

Ik denk dat deze veronderstelling in veel gevallen geldig is, maar vrij recent onderzoek naar verlies van neurale netwerken suggereert dat netwerken met een hoge complexiteit daadwerkelijk kunnen profiteren van lokale minima, omdat een netwerk dat het wereldwijde minimum vindt, overtraind zal zijn en daarom minder effectief bij het verwerken van nieuwe invoervoorbeelden.

Een ander probleem dat hier een rol speelt, is een oppervlaktefunctie die een zadelpunt wordt genoemd; u kunt een voorbeeld zien in de onderstaande plot. Het is mogelijk dat in de context van echte neurale netwerktoepassingen zadelpunten in het foutoppervlak in feite een ernstiger probleem zijn dan lokale minima.

Conclusie

Ik hoop dat je genoten hebt van deze discussie over lokale minima. In het volgende artikel bespreken we enkele technieken die een neuraal netwerk helpen het globale minimum te bereiken (als we dat inderdaad willen).