Praktische powerfactorcorrectie

Wanneer de noodzaak zich voordoet om te corrigeren voor een slechte arbeidsfactor in een wisselstroomsysteem, heeft u waarschijnlijk niet de luxe om de exacte inductantie van de belasting in Henrys te kennen die u voor uw berekeningen kunt gebruiken.

Misschien heb je het geluk een instrument te hebben dat een vermogensfactormeter wordt genoemd om u te vertellen wat de arbeidsfactor is (een getal tussen 0 en 1) en het schijnbare vermogen (dat kan worden berekend door een voltmeter-uitlezing in volt te nemen en te vermenigvuldigen met een ampèremeter-uitlezing in ampère).

In minder gunstige omstandigheden moet u mogelijk een oscilloscoop gebruiken om spannings- en stroomgolfvormen te vergelijken, waarbij u de faseverschuiving in graden meet. en het berekenen van de arbeidsfactor door de cosinus van die faseverschuiving.

Hoogstwaarschijnlijk hebt u toegang tot een wattmeter voor het meten van het werkelijke vermogen, waarvan u de aflezing kunt vergelijken met een berekening van het schijnbaar vermogen (door de metingen van de totale spanning en de totale stroom te vermenigvuldigen). Uit de waarden van werkelijk en schijnbaar vermogen kunt u het blindvermogen en de arbeidsfactor bepalen.

Voorbeeld probleem

Laten we een voorbeeldprobleem maken om te zien hoe dit werkt:(figuur hieronder)

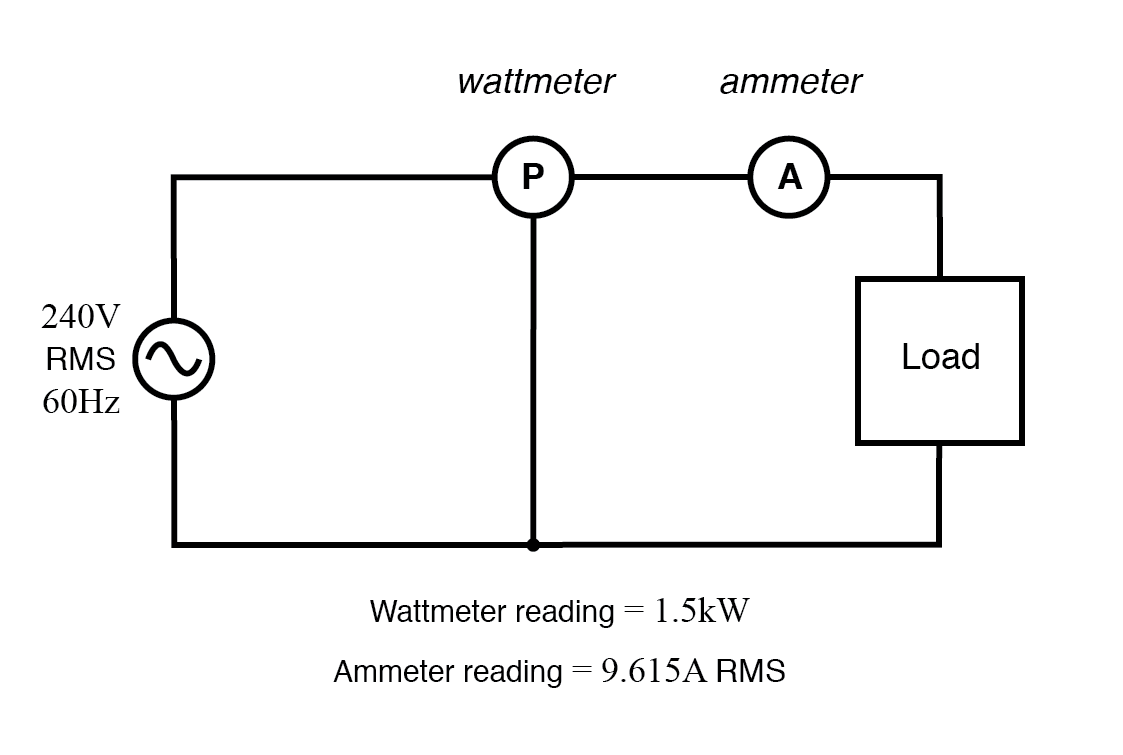
Wattmeter leest ware kracht; het product van voltmeter- en ampèremeter-uitlezingen levert schijnbaar vermogen op.

Hoe het schijnbare vermogen in kVA te berekenen

Eerst moeten we het schijnbare vermogen in kVA berekenen. We kunnen dit doen door de belastingsspanning te vermenigvuldigen met de belastingsstroom:

Zoals we kunnen zien, is 2.308 kVA een veel groter getal dan 1,5 kW, wat ons vertelt dat de arbeidsfactor in dit circuit nogal slecht is (aanzienlijk minder dan 1). Nu berekenen we de arbeidsfactor van deze belasting door het werkelijke vermogen te delen door het schijnbare vermogen:

Met behulp van deze waarde voor arbeidsfactor kunnen we een vermogensdriehoek tekenen en daaruit het reactieve vermogen van deze belasting bepalen:(figuur hieronder)

Reactief vermogen kan worden berekend op basis van werkelijk vermogen en schijnbaar vermogen.

Hoe de stelling van Pythagoras te gebruiken om onbekende driehoekshoeveelheid te bepalen

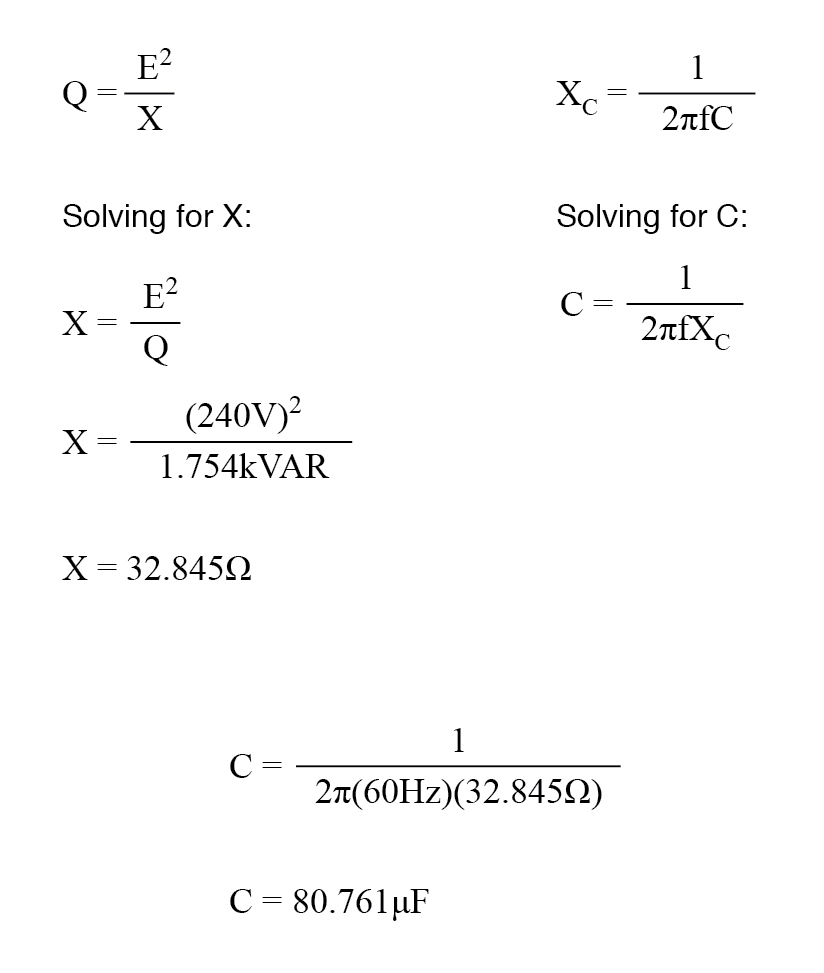
Om de onbekende driehoekshoeveelheid (reactief vermogen) te bepalen, gebruiken we de stelling van Pythagoras "achterwaarts", gezien de lengte van de hypotenusa (schijnbare kracht) en de lengte van de aangrenzende zijde (ware kracht):

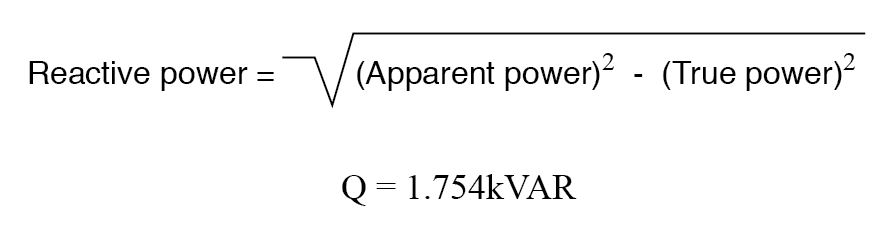
Hoe de arbeidsfactor te corrigeren met een condensator

Als deze belasting een elektromotor is of de meeste andere industriële AC-belasting, heeft deze een achterblijvende (inductieve) vermogensfactor, wat betekent dat we ervoor moeten corrigeren met een condensator van de juiste maat, parallel bedraad.

Nu we de hoeveelheid reactief vermogen (1,754 kVAR) weten, kunnen we de grootte van de condensator berekenen die nodig is om de effecten tegen te gaan:

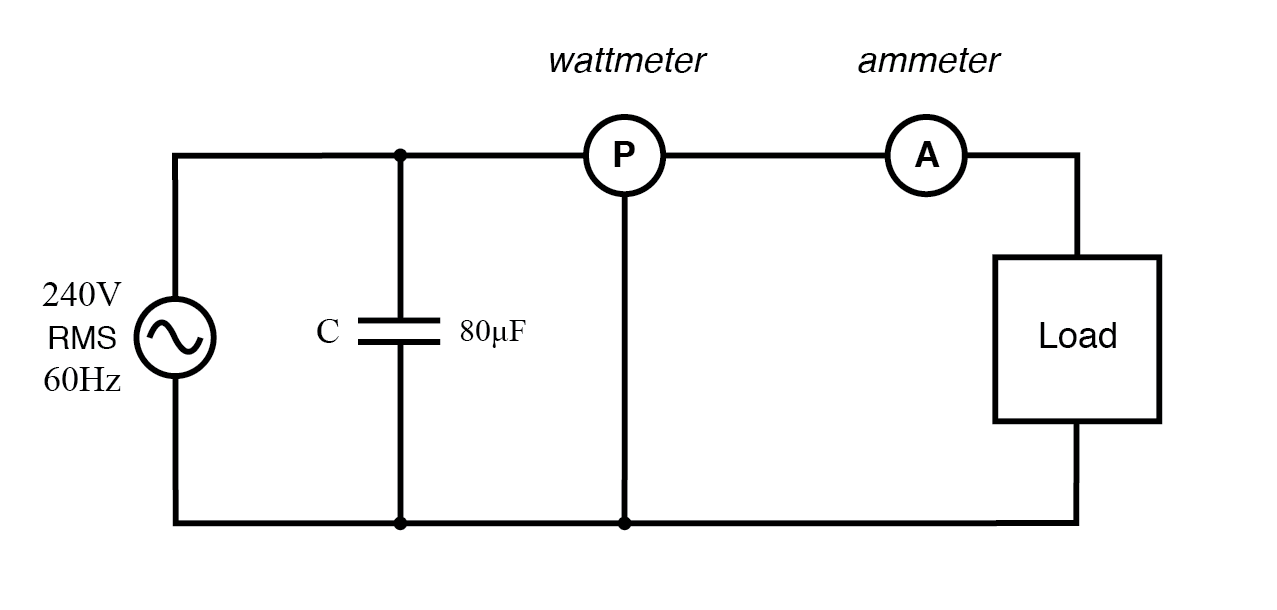
Als we dit antwoord afronden op 80 F, kunnen we die grootte van de condensator in het circuit plaatsen en de resultaten berekenen:(figuur hieronder)

Parallelle condensator corrigeert achterblijvende (inductieve) belasting.

Een condensator van 80 µF heeft een capacitieve reactantie van 33,157 Ω, wat een stroom geeft van 7,238 ampère en een bijbehorend reactief vermogen van 1,737 kVAR (voor de condensator alleen ). Aangezien de stroom van de condensator 180 ^o . is uit fase van de inductieve bijdrage van de belasting aan het stroomverbruik, zal het reactieve vermogen van de condensator direct worden afgetrokken van het reactieve vermogen van de belasting, wat resulteert in:

Deze correctie zal natuurlijk de hoeveelheid werkelijk vermogen die door de belasting wordt verbruikt niet veranderen, maar het zal resulteren in een aanzienlijke vermindering van het schijnbaar vermogen en van de totale stroom die uit de 240 Volt-bron wordt getrokken:(Figuur hieronder)

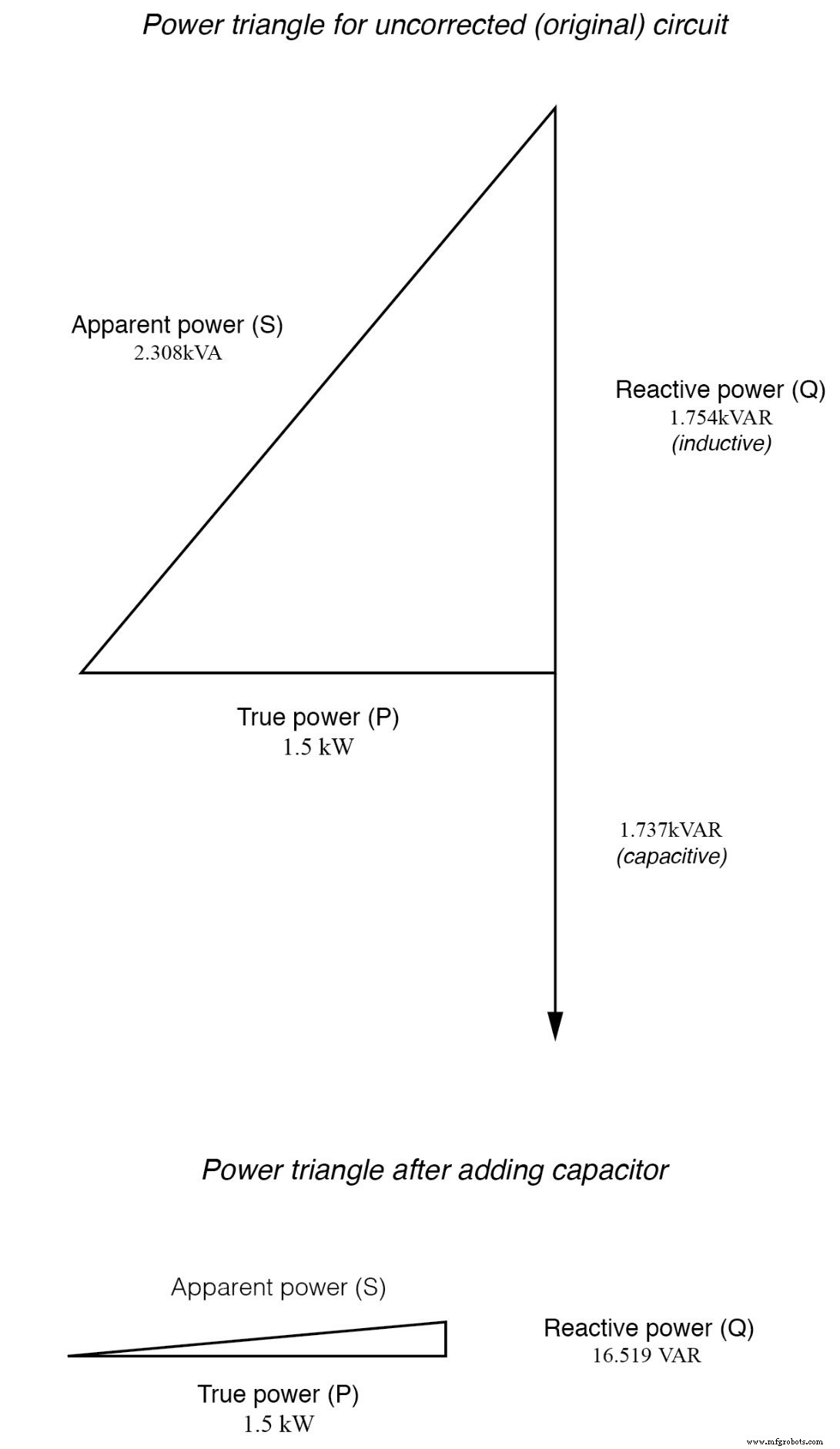
Vermogensdriehoek voor en na condensatorcorrectie.

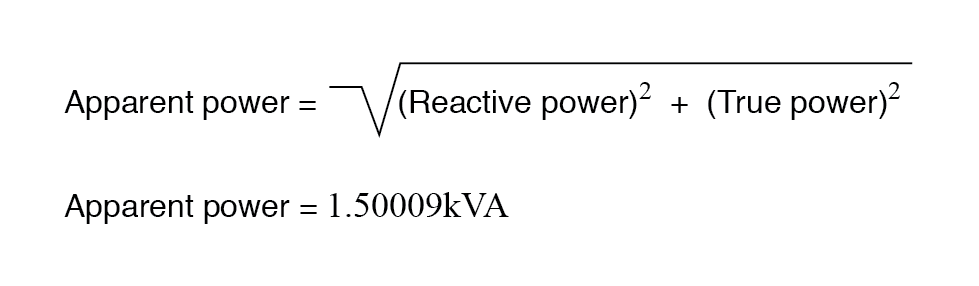
Het nieuwe schijnbare vermogen kan worden gevonden uit de waarden van het ware en nieuwe reactieve vermogen, met behulp van de standaardvorm van de stelling van Pythagoras:

GERELATEERD WERKBLAD:

• Werkblad Wisselstroom