Vermogen in resistieve en reactieve AC-circuits
Overweeg een circuit voor een enkelfasig wisselstroomsysteem, waarbij een 120 volt, 60 Hz wisselspanningsbron stroom levert aan een resistieve belasting:(figuur hieronder)
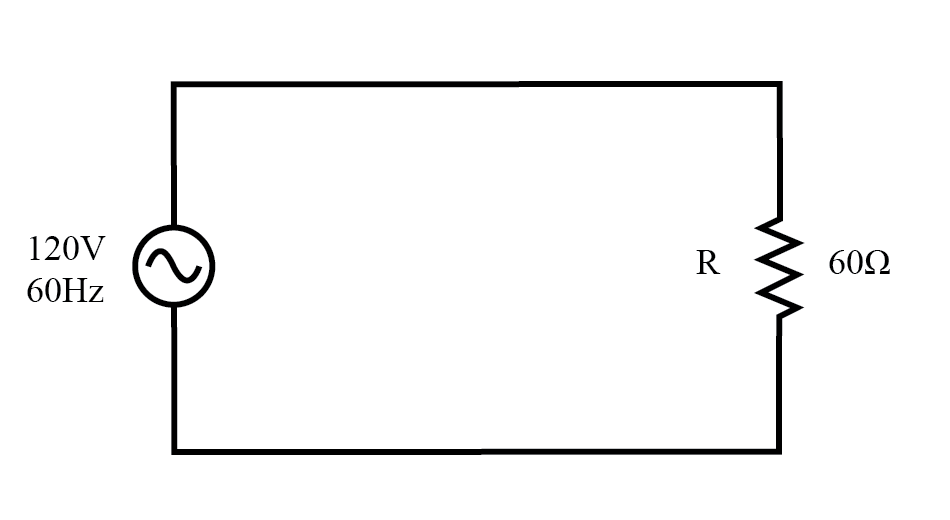
Ac-bron stuurt een puur resistieve belasting.
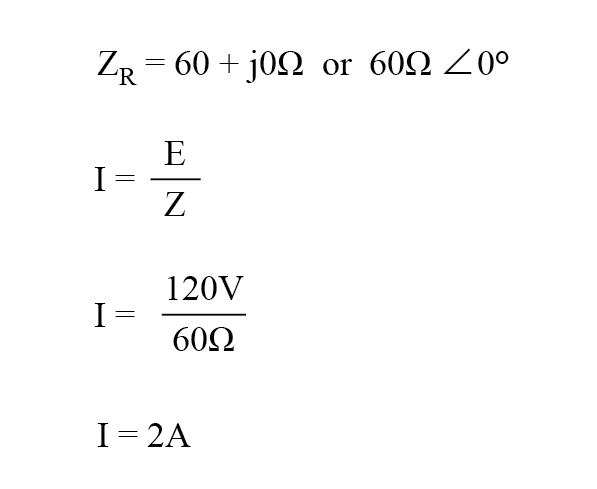
In dit voorbeeld zou de stroom naar de belasting 2 ampère zijn, RMS. Het gedissipeerde vermogen bij de belasting zou 240 watt zijn.
Omdat deze belasting puur resistief is (geen reactantie), is de stroom in fase met de spanning en lijken de berekeningen op die in een equivalent gelijkstroomcircuit.
Als we de spannings-, stroom- en vermogensgolfvormen voor dit circuit zouden plotten, zou het er als volgt uitzien.
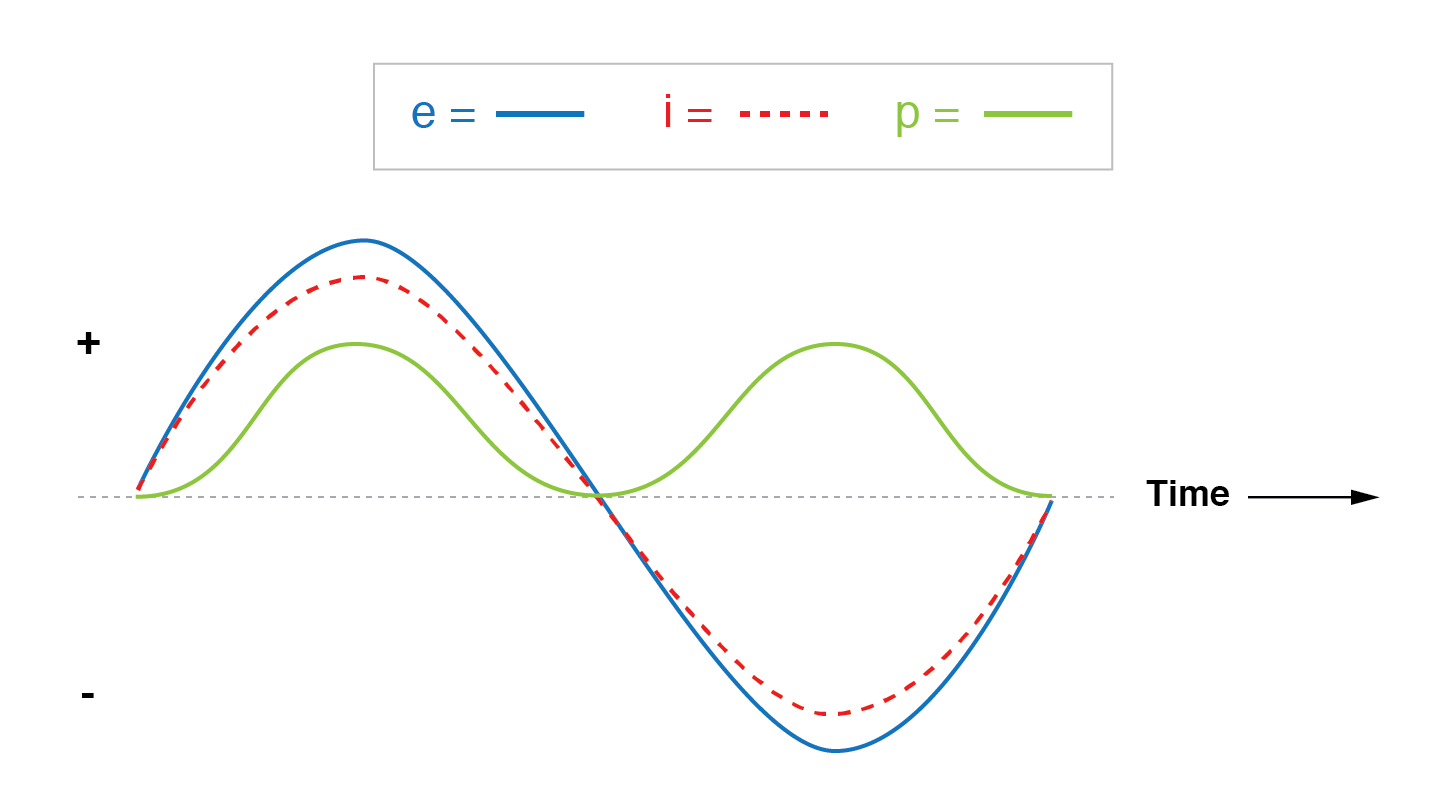
Stroom is in fase met spanning in een resistief circuit.
Merk op dat de golfvorm voor vermogen altijd positief is, nooit negatief voor dit resistieve circuit.
Dit betekent dat het vermogen altijd wordt gedissipeerd door de ohmse belasting en nooit wordt teruggestuurd naar de bron zoals bij reactieve belastingen. Als de bron een mechanische generator zou zijn, zou er 240 watt aan mechanische energie (ongeveer 1/3 pk) nodig zijn om de as te laten draaien.
Merk ook op dat de golfvorm voor vermogen niet dezelfde frequentie heeft als de spanning of stroom! De frequentie is eerder dubbel die van de spannings- of stroomgolfvormen.
Deze andere frequentie verbiedt onze uitdrukking van vermogen in een wisselstroomcircuit met dezelfde complexe (rechthoekige of polaire) notatie als gebruikt voor spanning, stroom en impedantie, omdat deze vorm van wiskundige symboliek onveranderlijke faserelaties impliceert.
Wanneer frequenties niet hetzelfde zijn, veranderen faserelaties voortdurend.
Hoe vreemd het ook mag lijken, de beste manier om door te gaan met AC-stroomberekeningen is het gebruik van scalar notatie en om relevante faserelaties met trigonometrie af te handelen.
AC-circuit met een puur reactieve belasting
Laten we ter vergelijking een eenvoudig AC-circuit met een puur reactieve belasting bekijken in de onderstaande afbeelding.
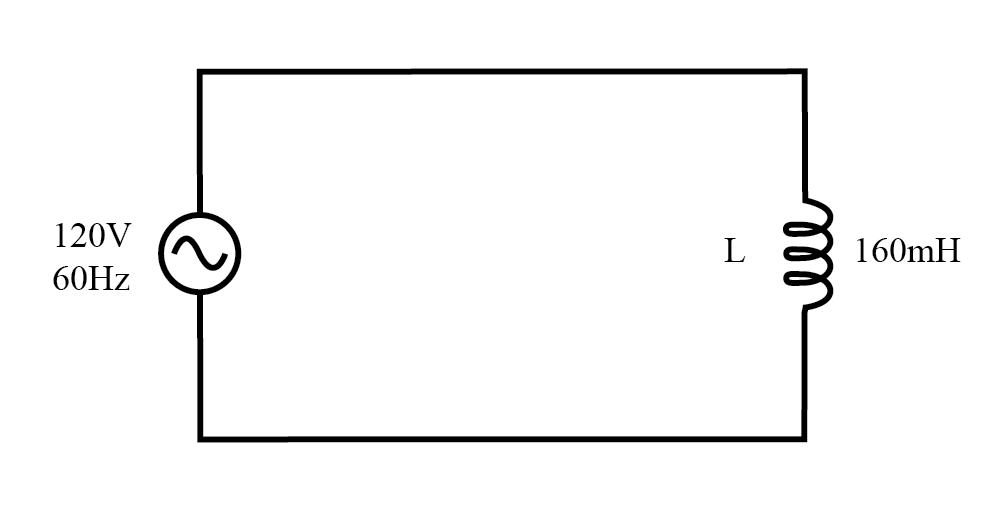
AC-circuit met een puur reactieve (inductieve) belasting.
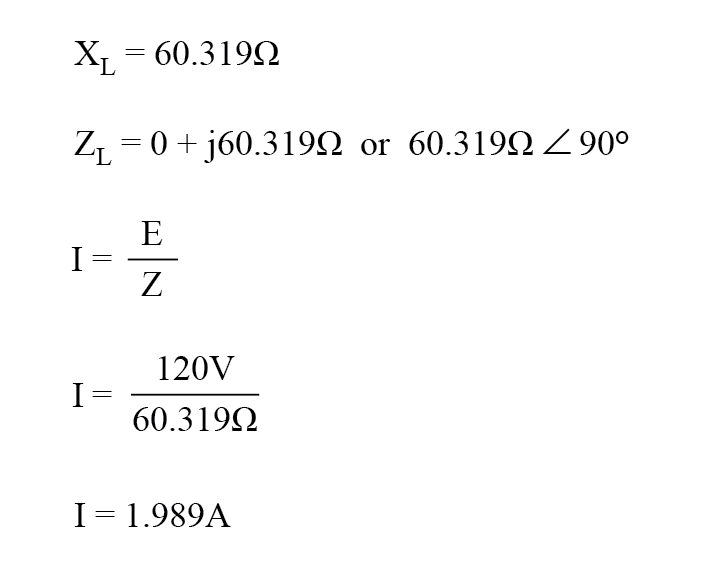
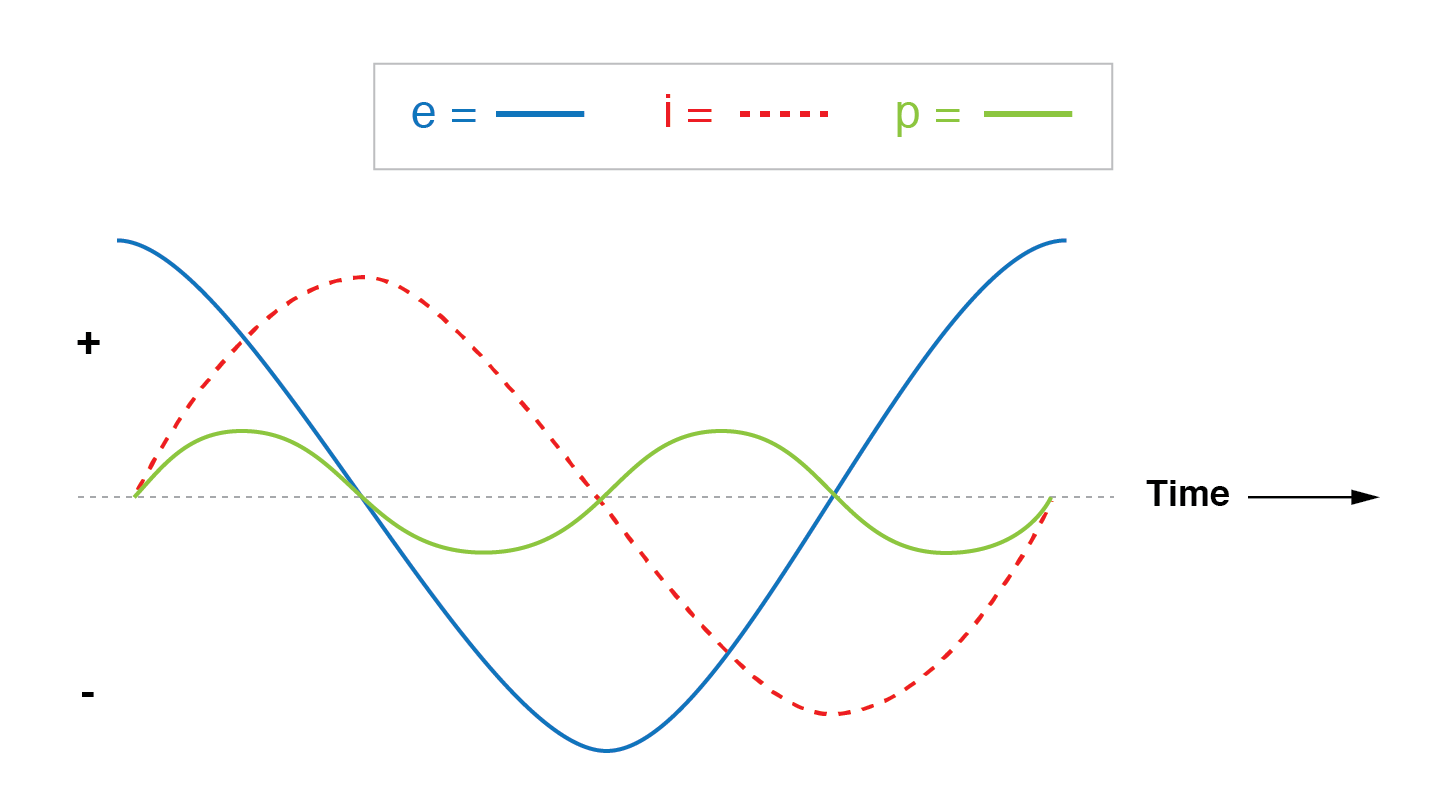
Het vermogen wordt niet gedissipeerd in een puur reactieve belasting. Hoewel het afwisselend wordt geabsorbeerd en teruggevoerd naar de bron.
Merk op dat het vermogen gelijkelijk wisselt tussen cycli van positief en negatief. (Figuur hierboven) Dit betekent dat er afwisselend stroom wordt geabsorbeerd en teruggevoerd naar de bron.
Als de bron een mechanische generator zou zijn, zou er (vrijwel) geen netto mechanische energie nodig zijn om de as te laten draaien, omdat er geen stroom door de belasting zou worden gebruikt.
De generatoras zou gemakkelijk kunnen draaien en de spoel zou niet zo warm worden als een weerstand.
AC-circuit met een resistieve en puur reactieve belasting
Laten we nu eens kijken naar een wisselstroomcircuit met een belasting bestaande uit zowel inductantie als weerstand in de onderstaande afbeelding.
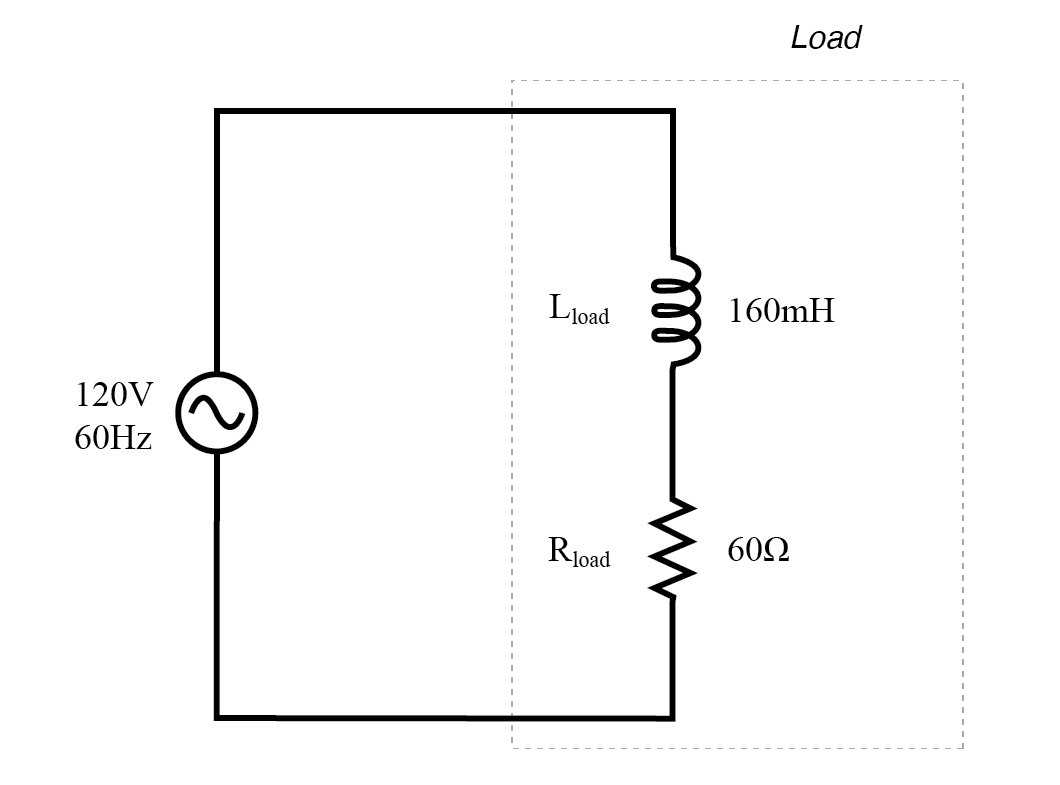
AC-circuit met zowel reactantie als weerstand.

Bij een frequentie van 60 Hz geven de 160 millihenrys inductantie ons 60,319 Ω inductieve reactantie.
Deze reactantie wordt gecombineerd met de weerstand van 60 om een totale belastingsimpedantie te vormen van 60 + j60.319 Ω, of 85.078 Ω ∠ 45.152 o . Als we ons niet bezighouden met fasehoeken (wat we op dit moment niet zijn), kunnen we de stroom in het circuit berekenen door de polaire grootte van de spanningsbron (120 volt) te nemen en deze te delen door de polaire grootte van de impedantie (85.078 ).
Met een voedingsspanning van 120 volt RMS is onze laadstroom 1.410 ampère. Dit is het cijfer dat een RMS-ampèremeter zou aangeven als deze in serie is geschakeld met de weerstand en de spoel.
We weten al dat reactieve componenten nul stroom dissiperen, omdat ze evengoed stroom opnemen van en stroom teruggeven aan de rest van het circuit.
Daarom zal elke inductieve reactantie in deze belasting eveneens nul vermogen dissiperen.
Het enige dat hier nog over is om het vermogen te dissiperen, is het resistieve deel van de belastingsimpedantie. Als we kijken naar de golfvormgrafiek van spanning, stroom en totaal vermogen voor dit circuit, zien we hoe deze combinatie werkt in de onderstaande afbeelding.

Een gecombineerd resistief/reactief circuit dissipeert meer stroom dan het teruggeeft aan de bron. De reactantie dissipeert geen vermogen; de weerstand wel.
Zoals bij elk reactief circuit, wisselt het vermogen in de loop van de tijd tussen positieve en negatieve momentane waarden.
In een puur reactief circuit is die afwisseling tussen positief en negatief vermogen gelijk verdeeld, wat resulteert in een netto vermogensdissipatie van nul. In circuits met gemengde weerstand en reactantie zoals deze, zal de vermogensgolfvorm echter nog steeds afwisselen tussen positief en negatief, maar de hoeveelheid positief vermogen zal de hoeveelheid negatief vermogen overschrijden.
Met andere woorden, de gecombineerde inductieve/resistieve belasting zal meer stroom verbruiken dan dat deze teruggaat naar de bron.
Kijkend naar de golfvormgrafiek voor vermogen, zou het duidelijk moeten zijn dat de golf meer tijd aan de positieve kant van de middellijn doorbrengt dan aan de negatieve, wat aangeeft dat er meer vermogen wordt geabsorbeerd door de belasting dan dat er wordt teruggevoerd naar het circuit.
Het weinige terugkeren van vermogen dat optreedt, is te wijten aan de reactantie; de onbalans van positief versus negatief vermogen is te wijten aan de weerstand omdat het energie buiten het circuit dissipeert (meestal in de vorm van warmte).
Als de bron een mechanische generator zou zijn, zou de hoeveelheid mechanische energie die nodig is om de as te laten draaien gelijk zijn aan het gemiddelde vermogen tussen de positieve en negatieve vermogenscycli.
Het wiskundig weergeven van vermogen in een wisselstroomcircuit is een uitdaging, omdat de vermogensgolf niet dezelfde frequentie heeft als spanning of stroom.
Bovendien betekent de fasehoek voor vermogen iets heel anders dan de fasehoek voor spanning of stroom. Terwijl de hoek voor spanning of stroom een relatieve verschuiving in timing vertegenwoordigt tussen twee golven vertegenwoordigt de fasehoek voor vermogen een verhouding tussen gedissipeerd vermogen en geretourneerd vermogen.
Vanwege deze manier waarop AC-vermogen verschilt van AC-spanning of -stroom, is het eigenlijk gemakkelijker om tot cijfers voor vermogen te komen door te rekenen met scalar hoeveelheden spanning, stroom, weerstand en reactantie dan het is om te proberen deze af te leiden uit vector , of complex hoeveelheden spanning, stroom en impedantie waarmee we tot nu toe hebben gewerkt.
BEOORDELING:
- In een puur resistief circuit wordt al het circuitvermogen gedissipeerd door de weerstand(en). Spanning en stroom zijn in fase met elkaar.
- In een puur reactief circuit wordt geen circuitvermogen gedissipeerd door de belasting(en). In plaats daarvan wordt stroom afwisselend geabsorbeerd en teruggevoerd naar de wisselstroombron. Spanning en stroom zijn 90° uit fase met elkaar.
- In een circuit dat bestaat uit gemengde weerstand en reactantie, zal er meer vermogen worden gedissipeerd door de belasting(en) dan geretourneerd, maar een deel van het vermogen zal zeker worden gedissipeerd en een deel zal alleen worden geabsorbeerd en geretourneerd. Spanning en stroom in zo'n circuit zullen uit fase zijn met een waarde ergens tussen 0° en 90°.
GERELATEERD WERKBLAD:
- Werkblad Wisselstroom
Industriële technologie
- Inleiding tot AC-circuits
- Inleiding tot digitale geïntegreerde schakelingen
- Voorbeelden van circuits en netlijsten
- Toelatende en interlockcircuits
- Gelijkrichterschakelingen
- Differentiator- en integratorcircuits
- Voedingscircuits
- Power in elektrische circuits
- Stroom, vermogen en koppel in aandrijvingen met variabele snelheid
- Wat is Power Hammers?- Types, ontwerp en bediening
- Power en HVAC/Klimaatregeling



