Harmonen in meerfasenstroomsystemen

In het hoofdstuk over signalen met gemengde frequenties hebben we het concept van harmonischen . verkend in AC-systemen:frequenties die gehele veelvouden zijn van de fundamentele bronfrequentie.

Bij wisselstroomsystemen waarbij de bronspanningsgolfvorm afkomstig van een wisselstroomgenerator (dynamo) verondersteld wordt een sinusgolf met één frequentie te zijn, onvervormd, mag er geen harmonische inhoud zijn. . . idealiter.

Niet-lineaire componenten op AC-systemen

Dit zou waar zijn, ware het niet voor niet-lineaire componenten . Niet-lineaire componenten trekken onevenredig veel stroom ten opzichte van de bronspanning, waardoor niet-sinusvormige stroomgolfvormen ontstaan.

Voorbeelden van niet-lineaire componenten zijn onder meer gasontladingslampen, vermogensregelingsapparaten voor halfgeleiders (diodes, transistors, SCR's, TRIAC's), transformatoren (de magnetisatiestroom van de primaire wikkeling is meestal niet-sinusvormig vanwege de B/H-verzadigingscurve van de kern), en elektromotoren (opnieuw, wanneer magnetische velden in de kern van de motor in de buurt van verzadigingsniveaus werken).

Zelfs gloeilampen genereren licht niet-sinusvormige stromen, omdat de weerstand van de gloeidraad tijdens de cyclus verandert als gevolg van snelle temperatuurschommelingen.

Zoals we hebben geleerd in het hoofdstuk over gemengde frequenties, moet elke vervorming van een anders sinusvormige golfvorm vormt de aanwezigheid van harmonische frequenties.

Wanneer de betreffende niet-sinusvormige golfvorm symmetrisch is boven en onder zijn gemiddelde middellijn, zullen de harmonische frequenties alleen oneven gehele veelvouden zijn van de fundamentele bronfrequentie, zonder even gehele veelvouden.

De meeste niet-lineaire belastingen produceren huidige golfvormen zoals deze, en dus zijn even harmonischen (2e, 4e, 6e, 8e, 10e, 12e, enz.) afwezig of slechts minimaal aanwezig in de meeste wisselstroomsystemen.

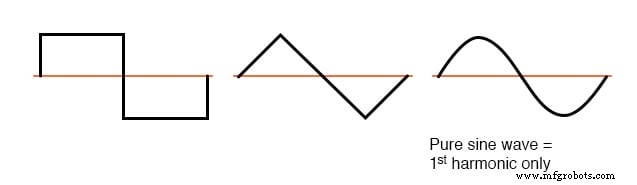
Voorbeelden van symmetrische golfvormen:alleen oneven harmonischen.

Voorbeelden van niet-symmetrische golfvormen met even harmonischen worden ter referentie getoond in de onderstaande afbeelding.

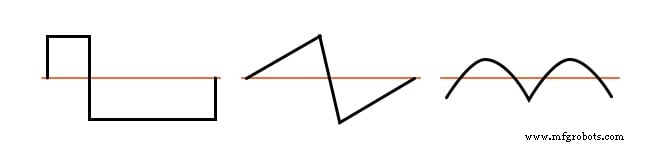
Voorbeelden van niet-symmetrische golfvormen—zelfs harmonischen aanwezig.

Hoewel de helft van de mogelijke harmonische frequenties wordt geëlimineerd door de typisch symmetrische vervorming van niet-lineaire belastingen, kunnen de oneven harmonischen nog steeds problemen veroorzaken. Sommige van deze problemen zijn algemeen voor alle voedingssystemen, enkelfasig of anderszins.

Oververhitting van de transformator door bijvoorbeeld wervelstroomverliezen kan optreden in elke Wisselstroomsysteem waar sprake is van aanzienlijke harmonische inhoud.

Er zijn echter enkele problemen die worden veroorzaakt door harmonische stromen die specifiek zijn voor meerfasige voedingssystemen, en het zijn deze problemen waaraan deze sectie specifiek is gewijd.

SPICE-simulatie met betrekking tot harmonische effecten

Het is handig om niet-lineaire belastingen in SPICE te kunnen simuleren om veel complexe wiskunde te vermijden en een meer intuïtief begrip van harmonische effecten te krijgen.

Lineaire AC-systeemsimulatie

Eerst beginnen we onze simulatie met een heel eenvoudig AC-circuit:een enkele sinusgolfspanningsbron met een puur lineaire belasting en alle bijbehorende weerstanden:

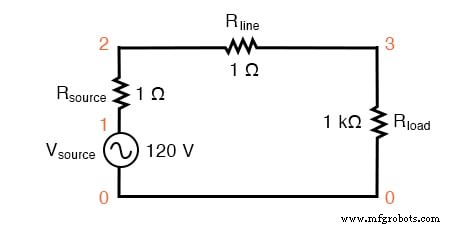
SPICE-circuit met een enkele sinusgolfbron.

De R_bron en R_regel weerstanden in dit circuit doen meer dan alleen de echte wereld nabootsen:ze bieden ook handige shuntweerstanden voor het meten van stromen in de SPICE-simulatie:door de spanning over een weerstand van 1 te lezen, krijgt u een directe indicatie van de stroom erdoorheen, aangezien E =IR .

Een SPICE-simulatie van dit circuit (SPICE-lijst:"lineaire belastingsimulatie") met Fourier-analyse op de spanning gemeten over R_lijn zou ons de harmonische inhoud van de lijnstroom van dit circuit moeten tonen. Omdat we volledig lineair van aard zijn, mogen we geen andere harmonischen verwachten dan de 1e (fundamentele) van 60 Hz, uitgaande van een 60 Hz-bron.

Zie SPICE-uitvoer "Fourier-componenten van transiënte respons v (2, 3)" en de onderstaande afbeelding.

lineaire belastingsimulatie vbron 1 0 sin(0 120 60 0 0) bron 1 2 1 rlijn 2 3 1 rbelasting 3 0 1k .opties itl5=0 .tran 0,5m 30m 0 1u .plot tran v(2,3) .vier 60 v(2,3) .einde 

 Fouriercomponenten van voorbijgaande respons v (2,3) gelijkstroomcomponent =4.028E-12 harmonische frequentie Fourier genormaliseerde fase genormaliseerd geen (hz) component component (deg) fase (deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 5.793E-12 0.000000 51.122 123.122 3 1.800E+02 7.407E-12 0.000000 -34.624 37.376 4 2.400E+02 9.056E-12 0.000000 4.267 76.267 5 3.000E+02 1.651E-11 0.000000 -83.461 -11.461 6 3.600E+02 3.931E-11 0.000000 36.399 108.399 7 4.200E+02 2.338E-11 0.000000 -41.343 30.657 8 4.800E+02 4.716E-11 0.000000 53.324 125.324 9 5.400E+02 3.453E-11 0.000000 21.691 93.691 totale harmonische vervorming =0,000000 procent 

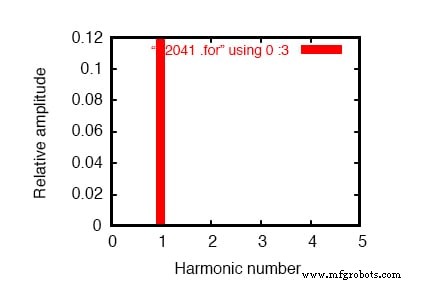
Frequentiedomeinplot van een enkele frequentiecomponent. Zie SPICE-lijst:"lineaire belastingsimulatie".

Een .plot-opdracht verschijnt in de SPICE-netlijst en normaal gesproken zou dit resulteren in een sinusgolfgrafiek. In dit geval heb ik echter met opzet de weergave van de golfvorm weggelaten omwille van de beknoptheid - het .plot-commando staat in de netlist om te voldoen aan een gril van de Fourier-transformatiefunctie van SPICE.

Geen enkele discrete Fourier-transformatie is perfect, en dus zien we zeer kleine harmonische stromen aangegeven (in het pico-amp-bereik!) Voor alle frequenties tot de 9e harmonische (in de tabel), wat zo ver gaat als SPICE gaat bij het uitvoeren van Fourier-analyse .

We tonen 0,1198 ampère (1.198E-01) voor de "Fourier-component" van de 1e harmonische, of de grondfrequentie, wat onze verwachte belastingsstroom is:ongeveer 120 mA, gegeven een bronspanning van 120 volt en een belastingsweerstand van 1 kΩ.

Eenvoudige niet-lineaire eenfase AC-systeemsimulatie

Vervolgens wil ik een niet-lineaire belasting simuleren om harmonische stromen te genereren. Dit kan op twee fundamenteel verschillende manieren. Een manier is om een ​​belasting te ontwerpen met behulp van niet-lineaire componenten zoals diodes of andere halfgeleiderapparaten die gemakkelijk te simuleren zijn met SPICE. Een andere is om enkele AC-stroombronnen parallel aan de belastingsweerstand toe te voegen.

De laatste methode heeft vaak de voorkeur van ingenieurs voor het simuleren van harmonischen, aangezien huidige bronnen van bekende waarde zich beter lenen voor wiskundige netwerkanalyse dan componenten met zeer complexe responskenmerken.

Aangezien we SPICE al het wiskundige werk laten doen, zou de complexiteit van een halfgeleidercomponent geen problemen voor ons veroorzaken, maar aangezien huidige bronnen kunnen worden afgesteld om elke willekeurige hoeveelheid stroom te produceren (een handige functie), zal ik kies de laatste benadering die wordt getoond in de onderstaande afbeelding en in de SPICE-lijst "Niet-lineaire belastingsimulatie".

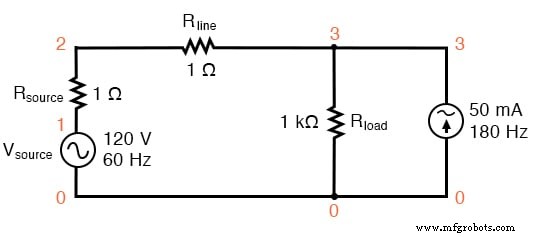
SPICE-circuit:60 Hz-bron met 3e harmonische toegevoegd.

 Simulatie van niet-lineaire belasting vsource 1 0 sin (0 120 60 0 0) bron 1 2 1 rlijn 2 3 1 rbelasting 3 0 1k i3har 3 0 zonde (0 50m 180 0 0) .opties itl5=0 .tran 0,5m 30m 0 1u .plot tran v(2,3) .vier 60 v(2,3) .einde 

In dit circuit hebben we een stroombron met een grootte van 50 mA en een frequentie van 180 Hz, wat drie keer de bronfrequentie van 60 Hz is. Parallel geschakeld met de belastingsweerstand van 1 kΩ, wordt de stroom opgeteld bij die van de weerstand om een ​​niet-sinusvormige totale lijnstroom te maken.

Ik zal de golfvormgrafiek in de onderstaande afbeelding laten zien, zodat u de effecten van deze 3e harmonische stroom op de totale stroom kunt zien, die normaal gesproken een gewone sinusgolf zou zijn.

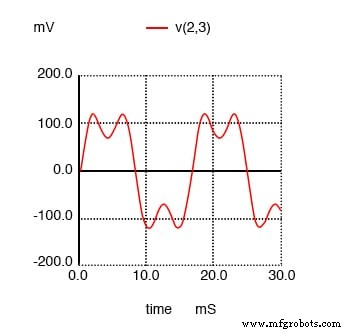
SPICE-tijddomeinplot met de som van de 60 Hz-bron en de 3e harmonische van 180 Hz.

Fourier componenten van voorbijgaande respons v(2,3) gelijkstroomcomponent =1.349E-11 harmonische frequentie Fourier genormaliseerde fase genormaliseerd geen (hz) component component (deg) fase (deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 1.609E-11 0.000000 67.570 139.570 3 1.800E+02 4.990E-02 0.416667 144.000 216.000 4 2.400E+02 1.074E-10 0.000000 -169.546 -97.546 5 3.000E+02 3.871E-11 0.000000 169.582 241.582 6 3.600E+02 5.736E-11 0.000000 140.845 212.845 7 4.200E+02 8.407E-11 0.000000 177.071 249.071 8 4.800E+02 1.329E-10 0.000000 156.772 228.772 9 5.400E+02 2.619E-10 0.000000 160.498 232.498 totale harmonische vervorming =41,666663 procent 

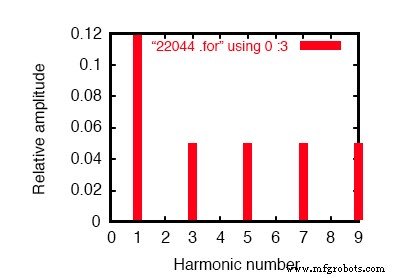
SPICE Fourier-plot met 60 Hz-bron en 3e harmonische van 180 Hz.

In de Fourier-analyse (zie de afbeelding hierboven en "Fourier-componenten van transiënte respons v (2, 3)") worden de gemengde frequenties niet gemengd en afzonderlijk gepresenteerd.

Hier zien we dezelfde 0,1198 ampère 60 Hz (fundamentele) stroom als in de eerste simulatie, maar in de 3e harmonische rij zien we 49,9 mA:onze 50 mA, 180 Hz stroombron aan het werk. Waarom zien we niet de hele 50 mA door de lijn?

Omdat die stroombron is aangesloten over de belastingsweerstand van 1 kΩ, wordt een deel van zijn stromen door de belasting geleid en gaat nooit via de lijn terug naar de bron. Het is een onvermijdelijk gevolg van dit soort simulatie, waarbij een deel van de belasting "normaal" is (een weerstand) en het andere deel wordt nagebootst door een stroombron.

Niet-lineaire eenfasige AC-systeemsimulatie met meerdere stroombronnen

Als we meer stroombronnen aan de "belasting" zouden toevoegen, zouden we een verdere vervorming van de lijnstroomgolfvorm van de ideale sinusgolfvorm zien, en elk van die harmonische stromen zou verschijnen in de Fourier-analyse-uitsplitsing. Zie de onderstaande afbeelding en de SPICE-lijst:"Niet-lineaire belastingsimulatie".

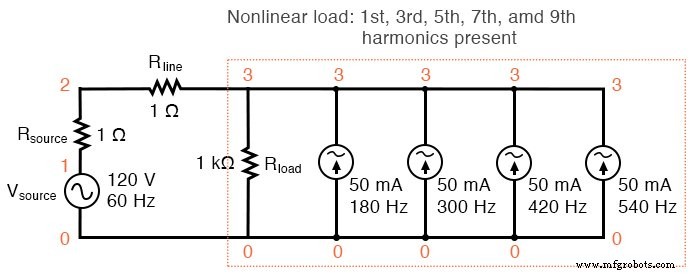
Niet-lineaire belasting:1e, 3e, 5e, 7e en 9e harmonischen aanwezig.

Niet-lineaire belastingsimulatie vbron 1 0 sin(0 120 60 0 0) bron 1 2 1 rlijn 2 3 1 rbelasting 3 0 1k i3har 3 0 zonde (0 50m 180 0 0) i5har 3 0 zonde (0 50m 300 0 0) i7har 3 0 sin(0 50m 420 0 0) i9har 3 0 sin(0 50m 540 0 0) .opties itl5=0 .tran 0,5m 30m 0 1u .plot tran v(2,3) .vier 60 v(2,3) .end 

Fourier componenten van voorbijgaande respons v(2,3) gelijkstroomcomponent =6.299E-11 harmonische frequentie Fourier genormaliseerde fase genormaliseerd geen (hz) component component (deg) fase (deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 1.900E-09 0.000000 -93.908 -21.908 3 1.800E+02 4.990E-02 0.416667 144.000 216.000 4 2.400E+02 5.469E-09 0.000000 -116.873 -44.873 5 3.000E+02 4.990E-02 0.416667 0.000 72.000 6 3.600E+02 6.271E-09 0.000000 85.062 157.062 7 4.200E+02 4.990E-02 0.416666 -144.000 -72.000 8 4.800E+02 2.742E-09 0.000000 -38.781 33.219 9 5.400E+02 4.990E-02 0.416666 72.000 144.000 totale harmonische vervorming =83,333296 procent 

Fourier-analyse:"Fourier-componenten van tijdelijke respons v(2,3)".

Zoals je kunt zien aan de Fourier-analyse (figuur hierboven), wordt elke harmonische stroombron gelijk weergegeven in de lijnstroom, elk met 49,9 mA. Tot nu toe is dit slechts een simulatie van een enkelfasig stroomsysteem.

Driefasige AC-systeemsimulatie

Het wordt interessanter als we er een driefasige simulatie van maken. Er worden twee Fourier-analyses uitgevoerd:een voor de spanning over een lijnweerstand en een voor de spanning over de neutrale weerstand.

Zoals eerder geeft het lezen van spanningen over vaste weerstanden van elk 1 directe indicaties van de stroom door die weerstanden. Zie de onderstaande afbeelding en de SPICE-lijst "Y-Y source/load 4-wire system with harmonics".

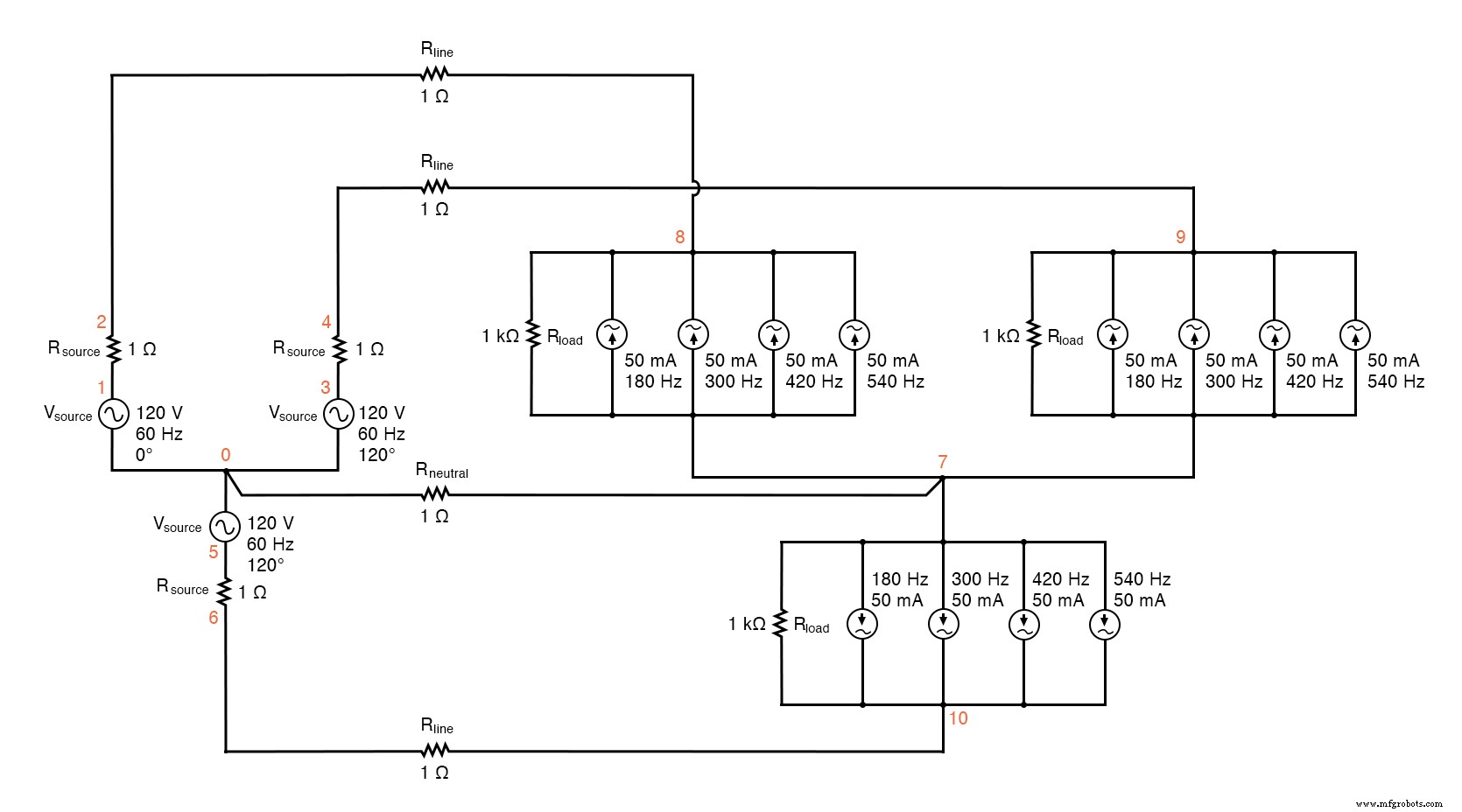
SPICE-circuit:analyse van "lijnstroom" en "neutrale stroom", Y-Y bron/belasting 4-draads systeem met harmonischen.

YY source/load 4-draads systeem met harmonischen * * fase1 spanningsbron en r (120 v /_ 0 deg) vbron1 1 0 sin(0 120 60 0 0) bron1 1 2 1 * * fase2 spanningsbron en r (120 v /_ 120 graden) vsource2 3 0 sin(0 120 60 5.55555m 0) bron2 3 4 1 * * phase3 spanningsbron en r (120 v /_ 240 deg) vsource3 5 0 sin(0 120 60 11.1111m 0) rsource3 5 6 1 * * lijn- en neutrale draadweerstanden rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 rneutraal 0 7 1 * * fase 1 van belasting rload1 8 7 1k i3har1 8 7 zonde (0 50m 180 0 0) i5har1 8 7 zonde (0 50m 300 0 0) i7har1 8 7 sin (0 50m 420 0 0) i9har1 8 7 sin (0 50m 540 0 0) * * fase 2 van belasting rload2 9 7 1k i3har2 9 7 sin (0 50m 180 5.55555m 0) i5har2 9 7 sin(0 50m 300 5.55555m 0) i7har2 9 7 sin (0 50m 420 5.55555m 0) i9har2 9 7 sin (0 50m 540 5.55555m 0) * * fase 3 van belasting rload3 10 7 1k i3har3 10 7 sin (0 50m 180 11.1111m 0) i5har3 10 7 sin (0 50m 300 11.1111m 0) i7har3 10 7 sin (0 50m 420 11.1111m 0) i9har3 10 7 sin (0 50m 540 11.1111m 0) * * analyse spul .opties itl5=0 .tran 0,5m 100m 12m 1u .plot tran v(2,8) .vier 60 v(2,8) .plot tran v(0,7) .vier 60 v(0,7) .einde 

Fourier-analyse van lijnstroom:

Fourier componenten van voorbijgaande respons v(2,8) gelijkstroomcomponent =-6.404E-12 harmonische frequentie Fourier genormaliseerde fase genormaliseerd geen (hz) component component (deg) fase (deg) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.218E-10 0.000000 172.985 172.985 3 1.800E+02 4.975E-02 0.415423 0.000 0.000 4 2.400E+02 4.236E-10 0.000000 166.990 166.990 5 3.000E+02 4.990E-02 0.416667 0.000 0.000 6 3.600E+02 1.877E-10 0.000000 -147.146 -147.146 7 4.200E+02 4.990E-02 0.416666 0.000 0.000 8 4.800E+02 2.784E-10 0.000000 -148.811 -148.811 9 5.400E+02 4.975E-02 0.415422 0.000 0.000 totale harmonische vervorming =83.209009 procent 

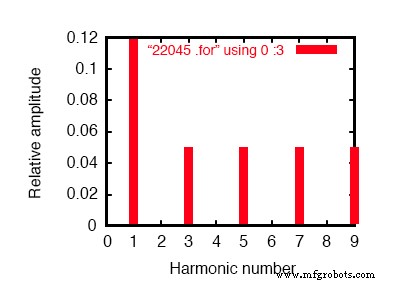
Fourier-analyse van lijnstroom in gebalanceerd Y-Y-systeem.

Fourier-analyse van neutrale stroom:

Fourier componenten van voorbijgaande respons v(0,7) gelijkstroomcomponent =1.819E-10 harmonische frequentie Fourier genormaliseerde fase genormaliseerd geen (hz) component component (deg) fase (deg) 1 6.000E+01 4.337E-07 1.000000 60.018 0.000 2 1.200E+02 1.869E-10 0.000431 91.206 31.188 3 1.800E+02 1.493E-01 344147.7638 -180.000 -240.018 4 2.400E+02 1.257E-09 0.002898 -21.103 -81.121 5 3.000E+02 9.023E-07 2.080596 119.981 59.963 6 3.600E+02 3.396E-10 0.000783 15.882 -44.136 7 4.200E+02 1.264E-06 2.913955 59,993 -0,025 8 4.800E+02 5.975E-10 0.001378 35.584 -24.434 9 5.400E+02 1.493E-01 344147.4889 -179.999 -240.017 

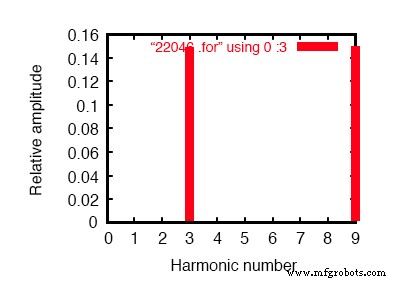
Vierder analyse van neutrale stroom toont behalve geen harmonischen! Vergelijk met lijnstroom in bovenstaande afbeelding.

Dit is een gebalanceerd YY-stroomsysteem, waarbij elke fase identiek is aan het eerder gesimuleerde enkelfasige wisselstroomsysteem. Het mag dan ook geen verrassing zijn dat de Fourier-analyse voor lijnstroom in één fase van het driefasensysteem bijna identiek is aan de Fourier-analyse voor lijnstroom in het enkelfasige systeem:een fundamentele (60 Hz) lijnstroom van 0,1198 ampère en oneven harmonische stromen van elk ongeveer 50 mA.

Zie de figuur hierboven en de Fourier-analyse:“Fourier-componenten van transiënte respons v(2,8)”

Wat hier verrassend zou moeten zijn, is de analyse voor de stroom van de nulleider, zoals bepaald door de spanningsval over de R_neutrale weerstand tussen SPICE-knooppunten 0 en 7.

In een gebalanceerde driefasige Y-belasting zouden we verwachten dat de neutrale stroom nul is. Elke fasestroom - die op zichzelf door de neutrale draad terug zou gaan naar de voedingsfase op de bron Y - zou elkaar moeten opheffen met betrekking tot de neutrale geleider omdat ze allemaal van dezelfde grootte zijn en allemaal 120 ° uit elkaar zijn verschoven.

In een systeem zonder harmonische stromen is dit is wat er gebeurt, waardoor er nul stroom door de nulleider blijft.

Effecten van harmonische stromen in het systeem

We kunnen echter niet hetzelfde zeggen voor harmonische stromen in hetzelfde systeem.

Merk op dat de grondfrequentie (60 Hz, of de 1e harmonische) stroom vrijwel afwezig is in de nulleider. Onze Fourier-analyse toont slechts 0,4337 µA van de 1e harmonische bij het lezen van de spanning over R_neutraal . Hetzelfde kan gezegd worden over de 5e en 7e harmonischen, die beide een verwaarloosbare grootte hebben.

Daarentegen zijn de 3e en 9e harmonischen sterk vertegenwoordigd binnen de nulleider, met elk 149,3 mA (1,493E-01 volt over 1 Ω)! Dit is bijna 150 mA, of drie keer de waarden van de huidige bronnen, afzonderlijk.

Met drie bronnen per harmonische frequentie in de belasting, lijkt het erop dat onze 3e en 9e harmonische stromen in elke fase toevoegen om de neutrale stroom te vormen. Zie Fourier-analyse:“Fourier-componenten van voorbijgaande respons v(0,7) ”

Tijddomein-grafiekanalyse

Dit is precies wat er gebeurt, hoewel het misschien niet duidelijk is waarom dit zo is.

De sleutel om dit te begrijpen wordt duidelijk gemaakt in een tijddomeingrafiek van fasestromen. Bestudeer deze grafiek van gebalanceerde fasestromen in de loop van de tijd, met een fasevolgorde van 1-2-3. (Figuur hieronder)

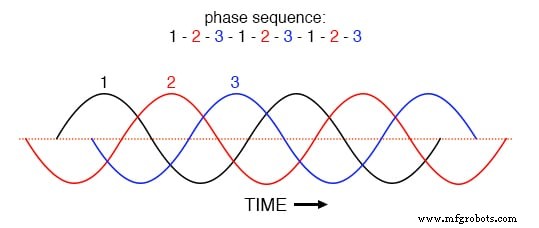
Fasereeks 1-2-3-1-2-3-1-2-3 van golven met gelijke tussenruimten.

Met de drie fundamentele golfvormen gelijkelijk verschoven over de tijdas van de grafiek, is het gemakkelijk te zien hoe ze elkaar zouden opheffen om een ​​resulterende stroom van nul in de neutrale geleider te geven. Laten we echter eens kijken hoe een 3e harmonische golfvorm voor fase 1 eruit zou zien als gesuperponeerd op de grafiek in de onderstaande afbeelding.

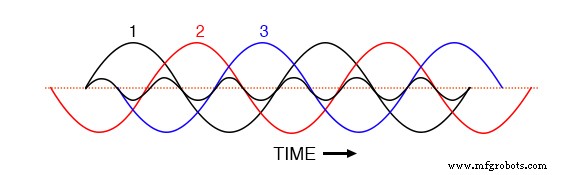
De derde harmonische golfvorm voor fase-1 gesuperponeerd op driefasige fundamentele golfvormen.

Merk op hoe deze harmonische golfvorm dezelfde faserelatie heeft met de 2e en 3e fundamentele golfvormen als met de 1e:in elke positieve halve cyclus van elke van de fundamentele golfvormen, vindt u precies twee positieve halve cycli en één negatieve halve cyclus van de harmonische golfvorm.

Wat dit betekent is dat de 3e harmonische golfvormen van drie 120° fase-verschoven fundamentele frequentie golfvormen in feite in fase zijn. met elkaar. Het faseverschuivingsgetal van 120° dat algemeen wordt aangenomen in driefasige wisselstroomsystemen is alleen van toepassing op de grondfrequenties, niet op hun harmonische veelvouden!

Als we alle drie de 3e harmonische golfvormen in dezelfde grafiek zouden plotten, zouden we ze precies overlappen en verschijnen als een enkele, uniforme golfvorm (vetgedrukt weergegeven in (figuur hieronder)

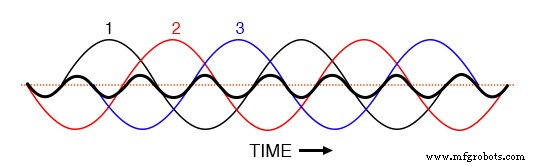
Derde harmonischen voor fasen 1, 2, 3 vallen allemaal samen wanneer ze worden gesuperponeerd op de fundamentele driefasige golfvormen.

Wiskundige analyse van de tijddomeingrafiek

Voor degenen die meer wiskundig geneigd zijn, kan dit principe symbolisch worden uitgedrukt. Stel dat A staat voor één golfvorm en B een andere, beide met dezelfde frequentie, maar qua fase 120° van elkaar verschoven. Laten we de 3e harmonische van elke golfvorm A' . noemen en B' , respectievelijk.

De faseverschuiving tussen A' en B' is niet 120° (dat is de faseverschuiving tussen A en B ), maar 3 keer zoveel, omdat de A' en B' golfvormen wisselen elkaar drie keer zo snel af als A en B . De verschuiving tussen golfvormen wordt alleen nauwkeurig uitgedrukt in termen van fasehoek wanneer dezelfde hoeksnelheid wordt aangenomen.

Bij het relateren van golfvormen met verschillende frequenties, is de meest nauwkeurige manier om faseverschuiving weer te geven in termen van tijd; en de time-shift tussen A' en B' komt overeen met 120° bij een frequentie die drie keer lager is, of 360° bij de frequentie van A' en B' . Een faseverschuiving van 360° is hetzelfde als een faseverschuiving van 0°, dat wil zeggen helemaal geen faseverschuiving.

Dus, A' en B' moeten in fase met elkaar zijn:

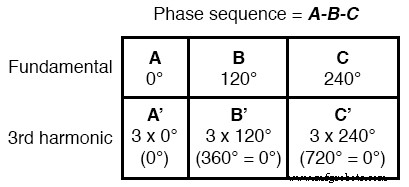
Deze eigenschap van de 3e harmonische in een driefasensysteem geldt ook voor alle gehele veelvouden van de 3e harmonische.

Dus niet alleen de 3e harmonische golfvormen van elke fundamentele golfvorm zijn in fase met elkaar, maar dat geldt ook voor de 6e harmonischen, de 9e harmonischen, de 12e harmonischen, de 15e harmonischen, de 18e harmonischen, de 21e harmonischen, enzovoort.

Aangezien alleen oneven harmonischen voorkomen in systemen waar golfvormvervorming symmetrisch is rond de middellijn - en de meeste niet-lineaire belastingen symmetrische vervorming veroorzaken - zijn even veelvouden van de 3e harmonische (6e, 12e, 18e, enz.) Over het algemeen niet significant, waardoor alleen de oneven veelvouden (3e, 9e, 15e, 21e, etc.) om aanzienlijk bij te dragen aan neutrale stromen.

In meerfasige voedingssystemen met een aantal andere fasen dan drie, treedt dit effect op met harmonischen van hetzelfde veelvoud. De harmonische stromen die bijvoorbeeld worden toegevoegd aan de neutrale geleider van een ster-verbonden 4-fasensysteem waarbij de faseverschuiving tussen fundamentele golfvormen 90 ° is, zijn de 4e, 8e, 12e, 16e, 20e, enzovoort.

Drievoudige harmonischen

Vanwege hun overvloed en betekenis in driefasige voedingssystemen, hebben de 3e harmonische en zijn veelvouden hun eigen speciale naam:triplen harmonischen .

Alle drievoudige harmonischen voegen zich bij elkaar in de nulleider van een 4-draads Y-aangesloten belasting. In voedingssystemen met een aanzienlijke niet-lineaire belasting, kunnen de drievoudige harmonische stromen groot genoeg zijn om neutrale geleiders oververhit te laten raken.

Dit is zeer problematisch, aangezien andere veiligheidsproblemen voorkomen dat neutrale geleiders overstroombeveiliging hebben, en er dus geen voorziening is voor automatische onderbreking van deze hoge stromen.

Analyse van de effecten van drievoudige harmonischen in een Y-Y-circuit

De volgende afbeelding laat zien hoe drievoudige harmonische stromen die bij de belasting worden gecreëerd, binnen de nulleider worden toegevoegd. Het symbool "ω" wordt gebruikt om de hoeksnelheid weer te geven en is wiskundig gelijk aan 2πf. Dus "ω" staat voor de grondfrequentie, "3ω" staat voor de 3e harmonische, "5ω" staat voor de 5e harmonische, enzovoort:(figuur hieronder)

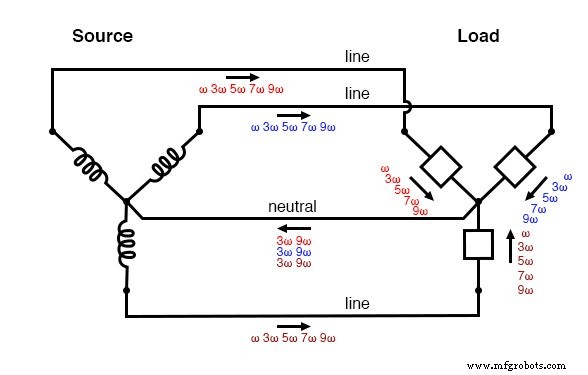
"Y-Y"Triple source/load:Harmonische stromen worden toegevoegd in de neutrale geleider.

In een poging om deze additieve triplenstromen te verminderen, zou men in de verleiding kunnen komen om de neutrale draad volledig te verwijderen. If there is no neutral wire in which triplen currents can flow together, then they won’t, right?

Unfortunately, doing so just causes a different problem:the load’s “Y” center-point will no longer be at the same potential as the source’s, meaning that each phase of the load will receive a different voltage than what is produced by the source.

We’ll re-run the last SPICE simulation without the 1 Ω R_neutral resistor and see what happens:

Y-Y source/load (no neutral) with harmonics * * phase1 voltage source and r (120 v / 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v / 120 deg) vsource2 3 0 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v / 240 deg) vsource3 5 0 sin(0 120 60 11.1111m 0) rsource3 5 6 1 * * line resistances rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 0 0) i5har1 8 7 sin(0 50m 300 0 0) i7har1 8 7 sin(0 50m 420 0 0) i9har1 8 7 sin(0 50m 540 0 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 5.55555m 0) i5har2 9 7 sin(0 50m 300 5.55555m 0) i7har2 9 7 sin(0 50m 420 5.55555m 0) i9har2 9 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 11.1111m 0) i5har3 10 7 sin(0 50m 300 11.1111m 0) i7har3 10 7 sin(0 50m 420 11.1111m 0) i9har3 10 7 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 12m 1u .plot tran v(2,8) .four 60 v(2,8) .plot tran v(0,7) .four 60 v(0,7) .plot tran v(8,7) .four 60 v(8,7) .einde 

Fourier analysis of line current:

Fourier components of transient response v(2,8) dc component =5.423E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.388E-10 0.000000 158.016 158.016 3 1.800E+02 3.136E-07 0.000003 -90.009 -90.009 4 2.400E+02 5.963E-11 0.000000 -111.510 -111.510 5 3.000E+02 4.990E-02 0.416665 0.000 0.000 6 3.600E+02 8.606E-11 0.000000 -124.565 -124.565 7 4.200E+02 4.990E-02 0.416668 0.000 0.000 8 4.800E+02 8.126E-11 0.000000 -159.638 -159.638 9 5.400E+02 9.406E-07 0.000008 -90.005 -90.005 total harmonic distortion =58.925539 percent 

Fourier analysis of voltage between the two “Y” center-points:

Fourier components of transient response v(0,7) dc component =6.093E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.453E-04 1.000000 60.018 0.000 2 1.200E+02 6.263E-08 0.000431 91.206 31.188 3 1.800E+02 5.000E+01 344147.7879 -180.000 -240.018 4 2.400E+02 4.210E-07 0.002898 -21.103 -81.121 5 3.000E+02 3.023E-04 2.080596 119.981 59.963 6 3.600E+02 1.138E-07 0.000783 15.882 -44.136 7 4.200E+02 4.234E-04 2.913955 59.993 -0.025 8 4.800E+02 2.001E-07 0.001378 35.584 -24.434 9 5.400E+02 5.000E+01 344147.4728 -179.999 -240.017 total harmonic distortion =************ percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(8,7) dc component =6.070E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 0.000 0.000 2 1.200E+02 6.231E-08 0.000000 90.473 90.473 3 1.800E+02 5.000E+01 0.417500 -180.000 -180.000 4 2.400E+02 4.278E-07 0.000000 -19.747 -19.747 5 3.000E+02 9.995E-02 0.000835 179.850 179.850 6 3.600E+02 1.023E-07 0.000000 13.485 13.485 7 4.200E+02 9.959E-02 0.000832 179.790 179.789 8 4.800E+02 1.991E-07 0.000000 35.462 35.462 9 5.400E+02 5.000E+01 0.417499 -179.999 -179.999 total harmonic distortion =59.043467 percent 

Strange things are happening, indeed.

First, we see that the triplen harmonic currents (3rd and 9th) all but disappear in the lines connecting a load to source. The 5th and 7th harmonic currents are present at their normal levels (approximately 50 mA), but the 3rd and 9th harmonic currents are of negligible magnitude.

Second, we see that there is a substantial harmonic voltage between the two “Y” center-points, between which the neutral conductor used to connect. According to SPICE, there are 50 volts of both 3rd and 9th harmonic frequency between these two points, which is definitely not normal in a linear (no harmonics), balanced Y system.

Finally, the voltage as measured across one of the load’s phases (between nodes 8 and 7 in the SPICE analysis) likewise shows strong triplen harmonic voltages of 50 volts each.

The figure below is a graphical summary of the aforementioned effects.

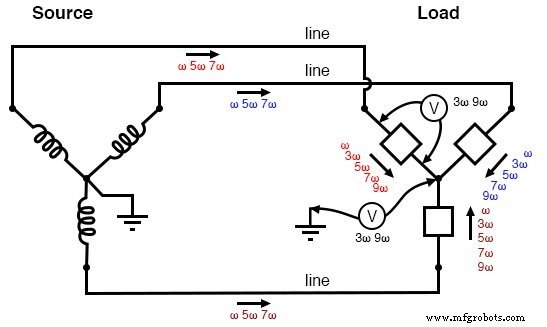
Three-wire “Y-Y” (no neutral) system:Triplen voltages appear between “Y” centers. Triplen voltages appear across load phases. Non-triplen currents appear in line conductors.

In summary, removal of the neutral conductor leads to a “hot” center-point on the load “Y”, and also to harmonic load phase voltages of equal magnitude, all comprised of triplen frequencies.

In the previous simulation where we had a 4-wire, Y-connected system, the undesirable effect from harmonics was excessive neutral current , but at least each phase of the load received voltage nearly free of harmonics.

Analysis of the Effects of Triplen Harmonics in a Delta-Wye(Y) Circuit

Since removing the neutral wire didn’t seem to work in eliminating the problems caused by harmonics, perhaps switching to a Δ configuration will. Let’s try a Δ source instead of a Y, keeping the load in its present Y configuration, and see what happens.

The measured parameters will be line current (voltage across R_line , nodes 0 and 8), load phase voltage (nodes 8 and 7), and source phase current (voltage across R_source , nodes 1 and 2). (Figuur hieronder)

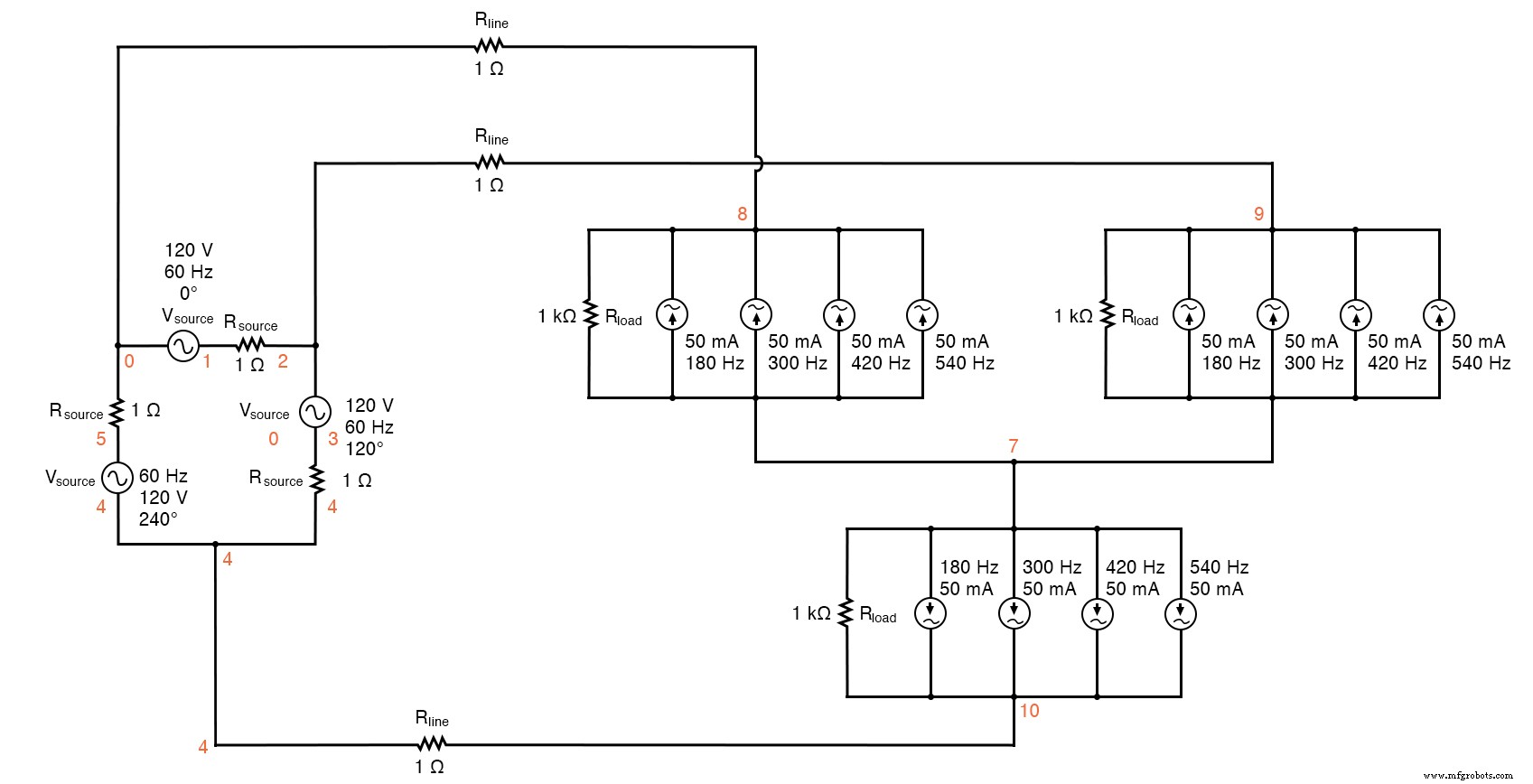
Delta-Y source/load with harmonics

Delta-Y source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 207.846 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 207.846 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 207.846 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 9.72222m 0) i5har1 8 7 sin(0 50m 300 9.72222m 0) i7har1 8 7 sin(0 50m 420 9.72222m 0) i9har1 8 7 sin(0 50m 540 9.72222m 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 15.2777m 0) i5har2 9 7 sin(0 50m 300 15.2777m 0) i7har2 9 7 sin(0 50m 420 15.2777m 0) i9har2 9 7 sin(0 50m 540 15.2777m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 4.16666m 0) i5har3 10 7 sin(0 50m 300 4.16666m 0) i7har3 10 7 sin(0 50m 420 4.16666m 0) i9har3 10 7 sin(0 50m 540 4.16666m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,8) v(8,7) v(1,2) .four 60 v(0,8) v(8,7) v(1,2) .einde 

Note:the following paragraph is for those curious readers who follow every detail of my SPICE netlists. If you just want to find out what happens in the circuit, skip this paragraph!

When simulating circuits having AC sources of differing frequency and differing phase, the only way to do it in SPICE is to set up the sources with a delay time or phase offset specified in seconds. Thus, the 0° source has these five specifying figures:“(0 207.846 60 0 0)”, which means 0 volts DC offset, 207.846 volts peak amplitude (120 times the square root of three, to ensure the load phase voltages remain at 120 volts each), 60 Hz, 0 time delay, and 0 damping factor.

The 120° phase-shifted source has these figures:“(0 207.846 60 5.55555m 0)”, all the same as the first except for the time delay factor of 5.55555 milliseconds, or 1/3 of the full period of 16.6667 milliseconds for a 60 Hz waveform.

The 240° source must be time-delayed twice that amount, equivalent to a fraction of 240/360 of 16.6667 milliseconds, or 11.1111 milliseconds.

This is for the Δ-connected source. The Y-connected load, on the other hand, requires a different set of time-delay figures for its harmonic current sources, because the phase voltages in a Y load are not in phase with the phase voltages of a Δ source.

If Δ source voltages VAC, VBA, and VCB are referenced at 0°, 120°, and 240°, respectively, then “Y” load voltages VA, VB, and VC will have phase angles of -30°, 90°, and 210°, respectively.

This is an intrinsic property of all Δ-Y circuits and not a quirk of SPICE. Therefore, when I specified the delay times for the harmonic sources, I had to set them at 15.2777 milliseconds (-30°, or +330°), 4.16666 milliseconds (90°), and 9.72222 milliseconds (210°).

One final note:when delaying AC sources in SPICE, they don’t “turn on” until their delay time has elapsed, which means any mathematical analysis up to that point in time will be in error. Consequently, I set the .tran transient analysis line to hold off analysis until 16 milliseconds after the start, which gives all sources in the netlist time to engage before any analysis takes place.

The result of this analysis is almost as disappointing as the last. (Figure below) Line currents remain unchanged (the only substantial harmonic content being the 5th and 7th harmonics), and load phase voltages remain unchanged as well, with a full 50 volts of triplen harmonic (3rd and 9th) frequencies across each load component.

Source phase current is a fraction of the line current, which should come as no surprise. Both 5th and 7th harmonics are represented there, with negligible triplen harmonics:

Fourier analysis of line current:

 Fourier components of transient response v(0,8) dc component =-6.850E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 150.000 0.000 2 1.200E+02 2.491E-11 0.000000 159.723 9.722 3 1.800E+02 1.506E-06 0.000013 0.005 -149.996 4 2.400E+02 2.033E-11 0.000000 52.772 -97.228 5 3.000E+02 4.994E-02 0.416682 30.002 -119.998 6 3.600E+02 1.234E-11 0.000000 57.802 -92.198 7 4.200E+02 4.993E-02 0.416644 -29.998 -179.998 8 4.800E+02 8.024E-11 0.000000 -174.200 -324.200 9 5.400E+02 4.518E-06 0.000038 -179.995 -329.995 total harmonic distortion =58.925038 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(8,7) dc component =1.259E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 150.000 0.000 2 1.200E+02 1.941E-07 0.000000 49.693 -100.307 3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998 4 2.400E+02 1.519E-07 0.000000 66.397 -83.603 5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112 6 3.600E+02 2.433E-07 0.000000 68.162 -81.838 7 4.200E+02 6.931E-02 0.000578 148.548 -1.453 8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E+02 5.000E+01 0.417221 90.006 -59.995 total harmonic distortion =59.004109 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(1,2) dc component =3.564E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 6.906E-02 1.000000 -0.181 0.000 2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493 3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815 4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390 5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815 6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745 7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694 9 5.400E+02 4.267E-06 0.000062 0.006 0.186 total harmonic distortion =59.031969 percent 

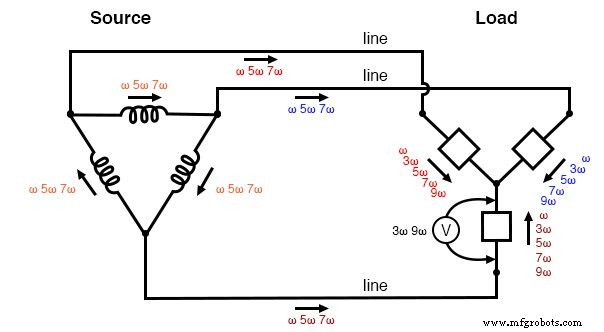
“Δ-Y” source/load:Triplen voltages appear across load phases. Non-triplen currents appear in line conductors and in source phase windings.

Really, the only advantage of the Δ-Y configuration from the standpoint of harmonics is that there is no longer a center-point at the load posing a shock hazard. Otherwise, the load components receive the same harmonically-rich voltages and the lines see the same currents as in a three-wire Y system.

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

If we were to reconfigure the system into a Δ-Δ arrangement, (Figure below) that should guarantee that each load component receives non-harmonic voltage, since each load phase would be directly connected in parallel with each source phase.

The complete lack of any neutral wires or “center points” in a Δ-Δ system prevents strange voltages or additive currents from occurring.

It would seem to be the ideal solution. Let’s simulate and observe, analyzing line current, load phase voltage, and source phase current. See SPICE listing:“Delta-Delta source/load with harmonics”, “Fourier analysis:Fourier components of transient response v(0,6)”, and “Fourier components of transient response v(2,1)”.

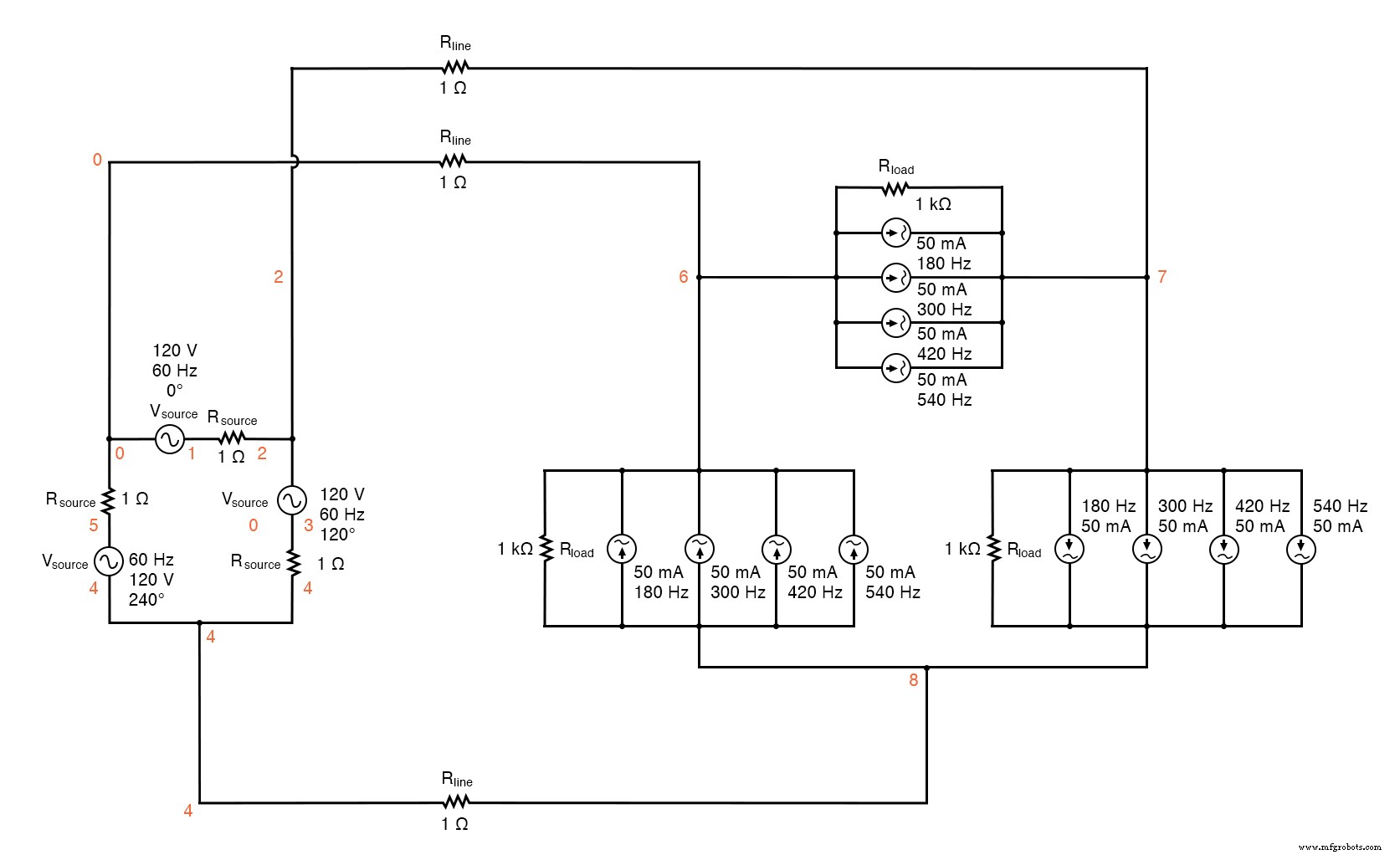
Delta-Delta source/load with harmonics.

Delta-Delta source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 120 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * * phase 1 of load rload1 7 6 1k i3har1 7 6 sin(0 50m 180 0 0) i5har1 7 6 sin(0 50m 300 0 0) i7har1 7 6 sin(0 50m 420 0 0) i9har1 7 6 sin(0 50m 540 0 0) * * phase 2 of load rload2 8 7 1k i3har2 8 7 sin(0 50m 180 5.55555m 0) i5har2 8 7 sin(0 50m 300 5.55555m 0) i7har2 8 7 sin(0 50m 420 5.55555m 0) i9har2 8 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 6 8 1k i3har3 6 8 sin(0 50m 180 11.1111m 0) i5har3 6 8 sin(0 50m 300 11.1111m 0) i7har3 6 8 sin(0 50m 420 11.1111m 0) i9har3 6 8 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,6) v(7,6) v(2,1) i(3har1) .four 60 v(0,6) v(7,6) v(2,1) .einde 

Fourier analysis of line current:

Fourier components of transient response v(0,6) dc component =-6.007E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 2.070E-01 1.000000 150.000 0.000 2 1.200E+02 5.480E-11 0.000000 156.666 6.666 3 1.800E+02 6.257E-07 0.000003 89.990 -60.010 4 2.400E+02 4.911E-11 0.000000 8.187 -141.813 5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E+02 8.626E-02 0.416669 150.001 0.001 8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E+02 1.877E-06 0.000009 89.987 -60.013 total harmonic distortion =58.925538 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(7,6) dc component =-5.680E-10 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.195E+02 1.000000 0.000 0.000 2 1.200E+02 1.039E-09 0.000000 144.749 144.749 3 1.800E+02 1.251E-06 0.000000 89.974 89.974 4 2.400E+02 4.215E-10 0.000000 36.127 36.127 5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E+02 3.752E-06 0.000000 89.905 89.905 total harmonic distortion =0.235702 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(2,1) dc component =-1.923E-12 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.194E-01 1.000000 179.940 0.000 2 1.200E+02 2.569E-11 0.000000 133.491 -46.449 3 1.800E+02 3.129E-07 0.000003 89.985 -89.955 4 2.400E+02 2.657E-11 0.000000 23.368 -156.571 5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939 6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E+02 9.385E-07 0.000008 89.991 -89.949 total harmonic distortion =58.961298 percent 

As predicted earlier, the load phase voltage is almost a pure sine-wave, with negligible harmonic content, thanks to the direct connection with the source phases in a Δ-Δ system.

But what happened to the triplen harmonics? The 3rd and 9th harmonic frequencies don’t appear in any substantial amount in the line current, nor in the load phase voltage, nor in the source phase current! We know that triplen currents exist because the 3rd and 9th harmonic current sources are intentionally placed in the phases of the load, but where did those currents go?

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

Remember that the triplen harmonics of 120° phase-shifted fundamental frequencies are in phase with each other.

Note the directions that the arrows of the current sources within the load phases are pointing, and think about what would happen if the 3rd and 9th harmonic sources were DC sources instead.

What we would have is currently circulating within the loop formed by the Δ-connected phases . This is where the triplen harmonic currents have gone:they stay within the Δ of the load, never reaching the line conductors or the windings of the source.

These results may be graphically summarized as such in the figure below.

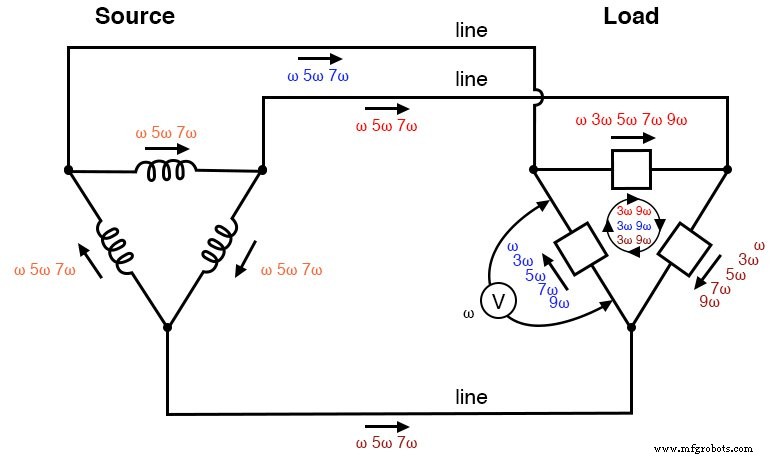
Δ-Δ source/load:Load phases receive undistorted sine wave voltages. Triplen currents are confined to circulate within load phases. Non-triplen currents appear in line conductors and in source phase windings.

This is a major benefit of the Δ-Δ system configuration:triplen harmonic currents remain confined in whatever set of components create them and do not “spread” to other parts of the system.

BEOORDELING:

• Nonlinear components are those that draw a non-sinusoidal (non-sine-wave) current waveform when energized by a sinusoidal (sine-wave) voltage. Since any distortion of an originally pure sine-wave constitutes harmonic frequencies, we can say that nonlinear components generate harmonic currents.
• When the sine-wave distortion is symmetrical above and below the average centerline of the waveform, the only harmonics present will be odd-numbered , not even-numbered.
• The 3rd harmonic, and integer multiples of it (6th, 9th, 12th, 15th) are known as triplen harmonics. They are in phase with each other, despite the fact that their respective fundamental waveforms are 120° out of phase with each other.
• In a 4-wire Y-Y system, triplen harmonic currents add within the neutral conductor.
• Triplen harmonic currents in a Δ-connected set of components circulate within the loop formed by the Δ.

GERELATEERDE WERKBLAD:

• Werkblad signalen met gemengde frequenties