Δ-Y en Y-Δ conversies

In veel circuittoepassingen komen we componenten tegen die op twee manieren met elkaar zijn verbonden om een ​​netwerk met drie terminals te vormen:de configuratie "Delta" of Δ (ook bekend als de "Pi" of π) en de "Y" ( ook bekend als de "T") configuratie.

Het is mogelijk om de juiste waarden van weerstanden te berekenen die nodig zijn om een ​​soort netwerk (Δ of Y) te vormen dat zich identiek gedraagt ​​als de andere soort, zoals alleen geanalyseerd op basis van de terminalverbindingen. Dat wil zeggen, als we twee afzonderlijke weerstandsnetwerken hadden, één Δ en één Y, elk met zijn weerstanden aan het zicht onttrokken, met niets anders dan de drie terminals (A, B en C) die voor het testen zichtbaar waren, zouden de weerstanden kunnen worden gedimensioneerd voor de twee netwerken, zodat er geen manier is om het ene netwerk elektrisch van het andere te onderscheiden. Met andere woorden, equivalente Δ- en Y-netwerken gedragen zich identiek.

Δ en Y conversievergelijkingen

Er zijn verschillende vergelijkingen die worden gebruikt om het ene netwerk naar het andere te converteren:

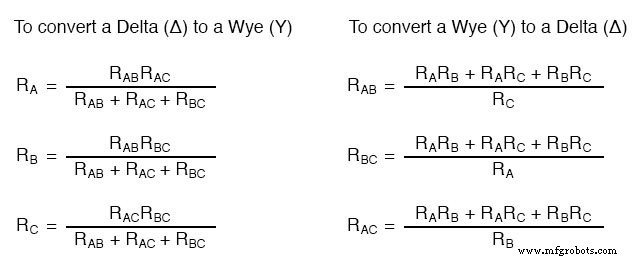
Δ- en Y-netwerken worden vaak gezien in driefasige wisselstroomvoedingssystemen (een onderwerp dat wordt behandeld in deel II van deze boekenreeks), maar zelfs dan zijn het meestal gebalanceerde netwerken (alle weerstanden gelijk in waarde) en conversie van de ene naar de andere dergelijke complexe berekeningen niet nodig zijn. Wanneer zou de gemiddelde technicus deze vergelijkingen ooit moeten gebruiken?

Toepassing van Δ en Y-conversie

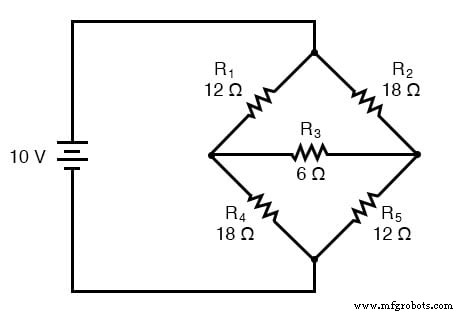
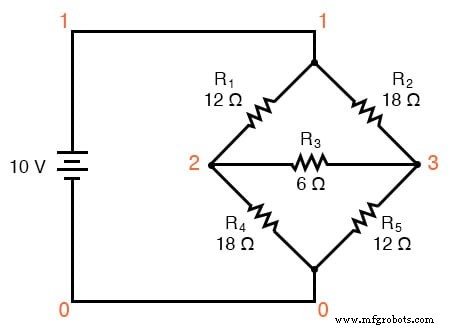
Een eerste toepassing voor Δ-Y-conversie is de oplossing van ongebalanceerde brugcircuits, zoals die hieronder:

De oplossing van dit circuit met vertakkingsstroom- of maasstroomanalyse is behoorlijk ingewikkeld, en noch de Millman- noch de superpositie-stellingen helpen daarbij, aangezien er maar één krachtbron is. We zouden de stelling van Thevenin of Norton kunnen gebruiken om R₃ . te behandelen als onze lading, maar wat zou dat leuk zijn?

Als we weerstanden R₁ . zouden behandelen , R₂ , en R₃ als verbonden in een Δ-configuratie (R_ab , R_ac , en R_bc , respectievelijk) en een equivalent Y-netwerk genereren om ze te vervangen, kunnen we van dit brugcircuit een (eenvoudiger) serie/parallel combinatiecircuit maken:

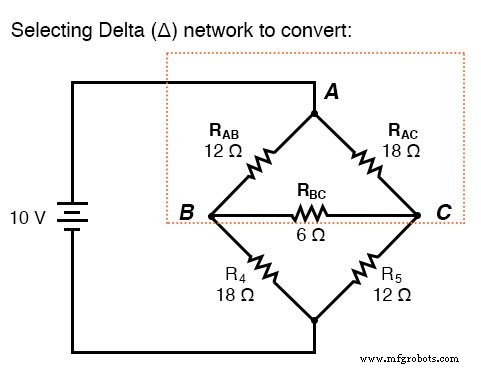
Na de Δ-Y conversie . . .

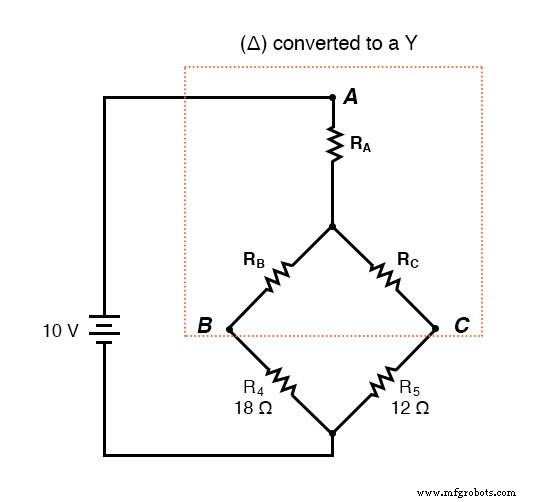
Als we onze berekeningen correct uitvoeren, zullen de spanningen tussen de punten A, B en C hetzelfde zijn in het geconverteerde circuit als in het oorspronkelijke circuit, en kunnen we die waarden terugzetten naar de oorspronkelijke brugconfiguratie.

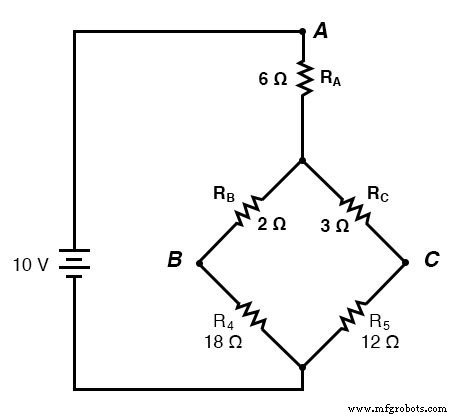
Weerstanden R₄ en R₅ , blijven natuurlijk hetzelfde bij respectievelijk 18 Ω en 12 Ω. Als we de schakeling nu analyseren als een serie/parallelle combinatie, komen we tot de volgende cijfers:

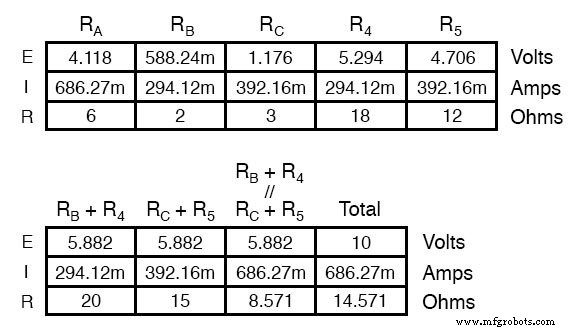
We moeten de spanningsdalingscijfers uit de bovenstaande tabel gebruiken om de spanningen tussen de punten A, B en C te bepalen, kijkend hoe ze optellen (of aftrekken, zoals het geval is met de spanning tussen de punten B en C):

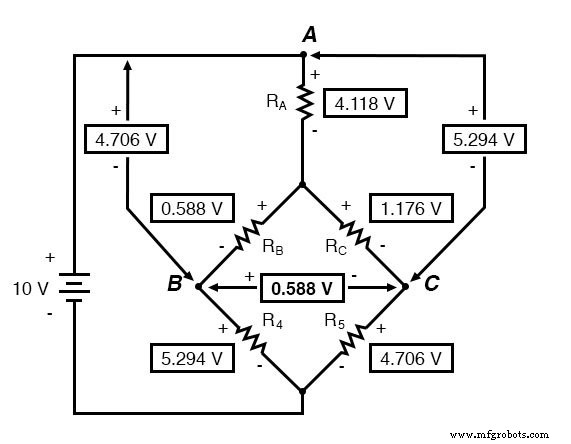
Nu we deze spanningen kennen, kunnen we ze overbrengen naar dezelfde punten A, B en C in het oorspronkelijke brugcircuit:

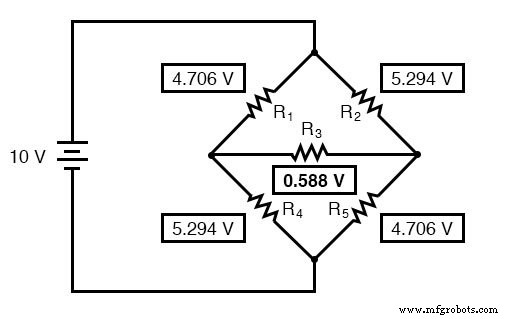
Spanning daalt over R₄ en R₅ , zijn natuurlijk precies hetzelfde als in het convertercircuit.

Op dit punt kunnen we deze spanningen nemen en weerstandsstromen bepalen door herhaald gebruik van de wet van Ohm (I=E/R):

Simulatie met SPICE

Een snelle simulatie met SPICE zal dienen om ons werk te verifiëren:

ongebalanceerd brugcircuit v1 1 0 r1 1 2 12 r2 1 3 18 r3 2 3 6 r4 2 0 18 r5 3 0 12 .dc v1 10 10 1 .print dc v(1,2) v(1,3) v(2,3) v(2,0) v(3,0) .einde v1 v(1,2) v(1,3) v(2,3) v(2) v(3) 1.000E+01 4.706E+00 5.294E+00 5.882E-01 5.294E+00 4.706E+00 

De spanningscijfers, zoals gelezen van links naar rechts, vertegenwoordigen spanningsdalingen over de vijf respectieve weerstanden, R₁ via R₅ . Ik had ook stromen kunnen laten zien, maar aangezien dat het invoegen van "dummy" spanningsbronnen in de SPICE-netlijst zou hebben vereist, en omdat we vooral geïnteresseerd zijn in het valideren van de Δ-Y-conversievergelijkingen en niet de wet van Ohm, is dit voldoende.

BEOORDELING:

• "Delta" (Δ)-netwerken zijn ook bekend als "Pi" (π)-netwerken.
• 'Y'-netwerken worden ook wel 'T'-netwerken genoemd.
• Δ- en Y-netwerken kunnen worden geconverteerd naar hun equivalente tegenhangers met de juiste weerstandsvergelijkingen. Met 'equivalent' bedoel ik dat de twee netwerken elektrisch identiek zullen zijn, gemeten vanaf de drie terminals (A, B en C).
• Een brugschakeling kan worden vereenvoudigd tot een serie/parallelschakeling door de helft ervan om te zetten van een Δ naar een Y-netwerk. Nadat spanningsdalingen tussen de oorspronkelijke drie verbindingspunten (A, B en C) zijn opgelost, kunnen die spanningen terug worden overgedragen naar het oorspronkelijke brugcircuit, over diezelfde equivalente punten.

GERELATEERD WERKBLAD:

• Werkblad Delta en Wye 3-fasenschakelingen