Circuitbedrading

Tot nu toe hebben we circuits met één batterij en één weerstand geanalyseerd zonder rekening te houden met de verbindingsdraden tussen de componenten, zolang er maar een compleet circuit wordt gevormd. Is de draadlengte of de "vorm" van het circuit van belang voor onze berekeningen? Laten we een paar schakelschema's bekijken om erachter te komen:

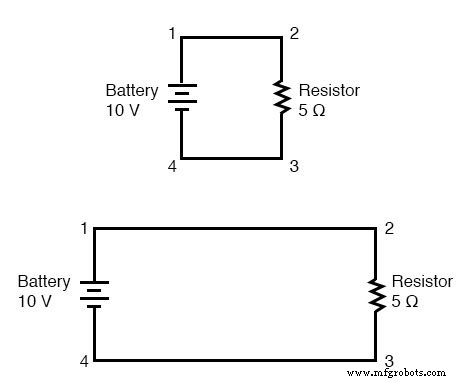
Wanneer we draden trekken die verbindingspunten in een elektrisch circuit verbinden, gaan we er meestal van uit dat die draden een verwaarloosbare weerstand hebben. Als zodanig dragen ze geen merkbaar effect bij aan de algehele weerstand van het circuit, en dus is de enige weerstand waarmee we te maken hebben de weerstand in de componenten. In de bovenstaande circuits komt de enige weerstand van de weerstanden van 5 , dus dat is alles wat we in onze berekeningen zullen overwegen.

In het echte leven doen metalen draden dat wel hebben weerstand (en stroombronnen ook!), maar die weerstanden zijn over het algemeen zo veel kleiner dan de weerstand die aanwezig is in de andere circuitcomponenten dat ze veilig kunnen worden genegeerd. Uitzonderingen op deze regel bestaan ​​in de bedrading van het voedingssysteem, waar zelfs zeer kleine hoeveelheden geleiderweerstand aanzienlijke spanningsdalingen kunnen veroorzaken bij normale (hoge) stroomniveaus.

Elektrisch gemeenschappelijke punten in een circuit

Als de weerstand van de verbindingsdraad heel weinig of geen is, kunnen we de verbonden punten in een circuit beschouwen als elektrisch algemeen . Dat wil zeggen dat de punten 1 en 2 in de bovenstaande circuits fysiek dicht bij elkaar of ver uit elkaar kunnen zijn aangesloten, en het maakt niet uit voor spannings- of weerstandsmetingen met betrekking tot die punten.

Hetzelfde geldt voor de punten 3 en 4. Het is alsof de uiteinden van de weerstand direct over de polen van de batterij zijn bevestigd, voor zover het onze berekeningen van de wet van Ohm en spanningsmetingen betreft.

Dit is handig om te weten, want het betekent dat u een schakelschema opnieuw kunt tekenen of een circuit opnieuw kunt bedraden, waarbij u de draden naar wens kunt inkorten of verlengen zonder de functie van het circuit merkbaar te beïnvloeden. Het enige dat telt is dat de componenten in dezelfde volgorde aan elkaar worden bevestigd.

Het betekent ook dat spanningsmetingen tussen sets van "elektrisch gemeenschappelijke" punten hetzelfde zullen zijn. Dat wil zeggen, de spanning tussen de punten 1 en 4 (direct over de batterij) zal hetzelfde zijn als de spanning tussen de punten 2 en 3 (direct over de weerstand). Bekijk het volgende circuit van dichtbij en probeer te bepalen welke punten met elkaar gemeen hebben:

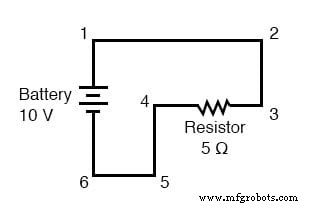
Hier hebben we slechts 2 componenten met uitzondering van de draden:de batterij en de weerstand. Hoewel de verbindingsdraden een ingewikkeld pad volgen bij het vormen van een compleet circuit, zijn er verschillende elektrisch gemeenschappelijke punten in het stroompad. Punten 1, 2 en 3 zijn allemaal gemeenschappelijk voor elkaar, omdat ze direct met elkaar verbonden zijn door middel van draad. Hetzelfde geldt voor de punten 4, 5 en 6.

De spanning tussen punt 1 en 6 is 10 volt, rechtstreeks afkomstig van de accu. Echter, aangezien punten 5 en 4 gemeenschappelijk zijn voor 6, en punten 2 en 3 gemeenschappelijk voor 1, bestaat diezelfde 10 volt ook tussen deze andere paren punten:

Tussen punten 1 en 4 =10 volt Tussen punten 2 en 4 =10 volt Tussen punten 3 en 4 =10 volt (direct over de weerstand) Tussen punten 1 en 5 =10 volt Tussen punten 2 en 5 =10 volt Tussen punten 3 en 5 =10 volt Tussen punten 1 en 6 =10 volt (direct over de accu) Tussen punten 2 en 6 =10 volt Tussen punten 3 en 6 =10 volt 

Aangezien elektrisch gemeenschappelijke punten met elkaar zijn verbonden door (nulweerstand) draad, is er geen significante spanningsval tussen hen, ongeacht de hoeveelheid stroom die van de ene naar de andere door die verbindingsdraad wordt geleid. Dus als we spanningen tussen gemeenschappelijke punten zouden lezen, zouden we (praktisch) nul moeten tonen:

Tussen punten 1 en 2 =0 volt Punten 1, 2 en 3 zijn tussen punten 2 en 3 =0 volt elektrisch gemeenschappelijk Tussen punten 1 en 3 =0 volt Tussen punten 4 en 5 =0 volt Punten 4, 5 en 6 zijn tussen punten 5 en 6 =0 volt elektrisch gemeenschappelijk Tussen punten 4 en 6 =0 volt 

De spanningsval berekenen met de wet van Ohm

Dit is ook wiskundig logisch. Met een 10 volt batterij en een weerstand van 5 zal de circuitstroom 2 ampère zijn. Omdat de draadweerstand nul is, kan de spanningsval over een continu stuk draad als zodanig worden bepaald door de wet van Ohm:

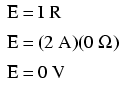
Het zou duidelijk moeten zijn dat de berekende spanningsval over elke ononderbroken draadlengte in een circuit waarvan wordt aangenomen dat de draad nul weerstand heeft, altijd nul zal zijn, ongeacht de grootte van de stroom, aangezien nul vermenigvuldigd met iets gelijk is aan nul.

Omdat gemeenschappelijke punten in een circuit dezelfde relatieve spannings- en weerstandsmetingen zullen vertonen, worden draden die gemeenschappelijke punten verbinden vaak met dezelfde aanduiding gelabeld. Dit wil niet zeggen dat de terminal aansluitpunten zijn hetzelfde gelabeld, alleen de aansluitdraden. Neem dit circuit als voorbeeld:

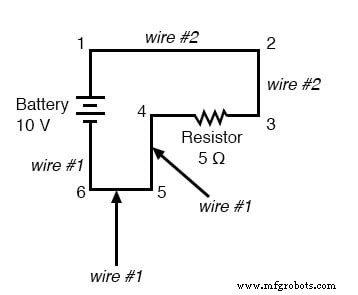
De punten 1, 2 en 3 zijn allemaal gemeenschappelijk voor elkaar, dus het draadverbindingspunt 1 tot 2 heeft hetzelfde label (draad 2) als het draadverbindingspunt 2 tot 3 (draad 2). In een echt circuit heeft de draad die zich uitstrekt van punt 1 naar 2 misschien niet eens dezelfde kleur of maat als de draad die verbindingspunt 2 naar 3 verbindt, maar ze moeten exact hetzelfde label dragen. Hetzelfde geldt voor de draden die de punten 6, 5 en 4 verbinden.

Spanningsval moet gelijk zijn aan nul in gemeenschappelijke punten

Wetende dat elektrisch gemeenschappelijke punten nul spanningsval tussen hen hebben, is een waardevol principe voor probleemoplossing. Als ik de spanning meet tussen punten in een circuit die verondersteld worden gemeenschappelijk te zijn, zou ik nul moeten lezen.

Als ik echter een aanzienlijke spanning tussen die twee punten lees, dan weet ik met zekerheid dat ze niet direct met elkaar verbonden kunnen worden. Als die punten verondersteld zijn elektrisch gemeenschappelijk zijn, maar ze registreren anders, dan weet ik dat er een "open storing" is tussen die punten.

Nulspanning betekent technisch gezien verwaarloosbare spanning

Een laatste opmerking:voor de meeste praktische doeleinden kan worden aangenomen dat draadgeleiders van begin tot eind geen weerstand hebben. In werkelijkheid zal er echter altijd een kleine hoeveelheid weerstand zijn langs de lengte van een draad, tenzij het een supergeleidende draad is. Als we dit weten, moeten we in gedachten houden dat de principes die hier worden geleerd over elektrisch gemeenschappelijke punten allemaal in hoge mate geldig zijn, maar niet in een absoluut diploma.

Dat wil zeggen, de regel dat elektrisch gemeenschappelijke punten gegarandeerd nul spanning hebben, wordt nauwkeuriger als zodanig vermeld:elektrisch gemeenschappelijke punten hebben heel weinig spanning viel tussen hen. Dat kleine, vrijwel onvermijdelijke spoor van weerstand dat in elk stuk verbindingsdraad wordt aangetroffen, zal ongetwijfeld een kleine spanning over de lengte ervan creëren terwijl er stroom doorheen wordt geleid.

Zolang je begrijpt dat deze regels zijn gebaseerd op ideale omstandigheden, zult u niet perplex staan ​​als u een aandoening tegenkomt die een uitzondering op de regel lijkt te zijn.

BEOORDELING:

• Aansluitdraden in een circuit worden verondersteld geen weerstand te hebben, tenzij anders vermeld.
• Draden in een circuit kunnen worden ingekort of verlengd zonder de functie van het circuit te beïnvloeden - het enige dat telt is dat de componenten in dezelfde volgorde aan elkaar worden bevestigd.
• Punten die rechtstreeks met elkaar zijn verbonden in een circuit door nulweerstand (draad) worden beschouwd als elektrisch algemeen .
• Elektrisch gemeenschappelijke punten, met nul weerstand ertussen, hebben nul spanning ertussen, ongeacht de grootte van de stroom (idealiter).
• De spannings- of weerstandswaarden waarnaar wordt verwezen tussen sets van elektrisch gemeenschappelijke punten zullen hetzelfde zijn.
• Deze regels zijn van toepassing op ideal omstandigheden, waarbij wordt aangenomen dat verbindingsdraden absoluut geen weerstand hebben. In het echte leven zal dit waarschijnlijk niet het geval zijn, maar de draadweerstanden moeten laag genoeg zijn zodat de hier vermelde algemene principes nog steeds gelden.

GERELATEERDE WERKBLAD:

• Werkblad Eenvoudige circuits
• Werkblad elementair circuit
• Werkblad spanningsdeler circuit