Grotere Karnaugh-kaarten met 5 en 6 variabelen

Grotere Karnaugh-kaarten verminderen grotere logische ontwerpen. Hoe groot is groot genoeg? Dat hangt af van het aantal ingangen, fan-ins , naar het logische circuit in kwestie. Een van de grote bedrijven in programmeerbare logica heeft een antwoord.

Altera's eigen gegevens, geëxtraheerd uit de bibliotheek met klantontwerpen, ondersteunen de waarde van heterogeniteit. Door logische kegels te onderzoeken, ze in kaart te brengen op LUT-gebaseerde knooppunten en ze te sorteren op het aantal ingangen dat het beste zou zijn op elk knooppunt, ontdekte Altera dat de verdeling van fan-ins bijna vlak was tussen twee en zes ingangen, met een mooie piek om vijf uur.

Het antwoord is niet meer dan zes ingangen voor bijna alle ontwerpen en vijf ingangen voor het gemiddelde logische ontwerp. De vijf variabele Karnaugh-kaart volgt.

Vijf variabele K-map

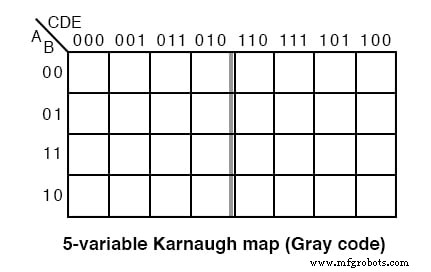
De oudere versie van de vijf variabele K-map, een Gray Code-kaart of reflectiekaart, wordt hierboven weergegeven. De bovenkant (en zijkant voor een kaart met 6 variabelen) van de kaart is genummerd in volledige grijze code. De grijze code weerspiegelt ongeveer het midden van de code. Deze stijlkaart is te vinden in oudere teksten. De nieuwere voorkeursstijl staat hieronder.

Overlay-versie van de K-map

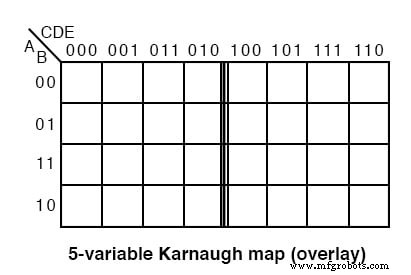
De overlay-versie van de Karnaugh-kaart, hierboven weergegeven, is eenvoudig twee (vier voor een kaart met 6 variabelen) identieke kaarten, behalve het meest significante deel van het 3-bits adres bovenaan.

Als we naar de bovenkant van de kaart kijken, zien we dat de nummering anders is dan de vorige Gray code-kaart. Als we het meest significante cijfer van de 3-cijferige getallen negeren, wordt de reeks 00, 01, 11, 10 staat aan de kop van beide subkaarten van de overlaykaart. De reeks van acht 3-cijferige nummers is geen grijze code. Hoewel de reeks van vier van de minst significante twee bits dat wel is.

Laten we onze Karnaugh-kaart met 5 variabelen gebruiken. Ontwerp een circuit met een 5-bits binaire ingang (A, B, C, D, E), waarbij A de MSB is (Most Significant Bit). Het moet een uitvoerlogica Hoog produceren voor elk priemgetal dat in de invoergegevens wordt gedetecteerd.

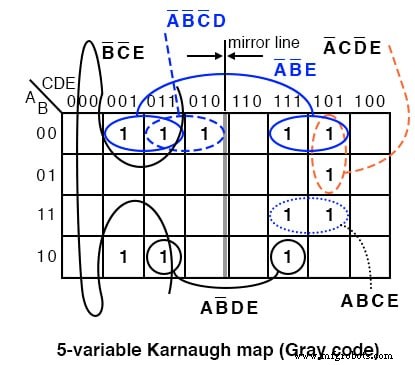
We tonen de oplossing hierboven op de oudere grijze code (reflectie) kaart ter referentie. De priemgetallen zijn (1,2,3,5,7,11,13,17,19,23,29,31). Plot een 1 in elke corresponderende cel. Ga vervolgens verder met het groeperen van de cellen. Eindig met het schrijven van het vereenvoudigde resultaat.

Merk op dat 4-cellige groep A'B'E bestaat uit twee paar cellen aan beide zijden van de spiegellijn. Hetzelfde geldt voor de 2-cellige groep AB'DE. Het is een groep van 2-cellen door te worden gereflecteerd rond de spiegellijn. Zoek bij gebruik van deze versie van de K-map naar spiegelbeelden in de andere helft van de kaart.

Uit =A'B'E + B'C'E + A'C'DE + A'CD'E + ABCE + AB'DE + A'B'C'D

Hieronder tonen we de meest voorkomende versie van de kaart met 5 variabelen, de overlay-kaart.

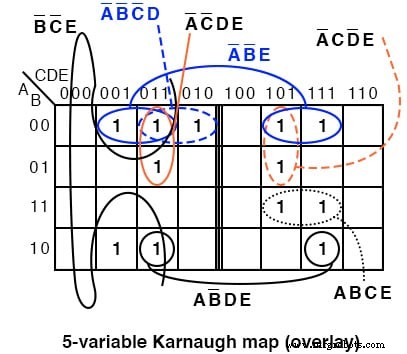
Als we de patronen in de twee kaarten vergelijken, worden sommige cellen in de rechterhelft van de kaart verplaatst, omdat de adressering aan de bovenkant van de kaart anders is. We moeten ook een andere benadering kiezen om overeenkomsten tussen de twee helften van de kaart te ontdekken.

Leg de ene helft van de kaart over de andere helft. Elke overlap van de bovenste kaart naar de onderste kaart is een potentiële groep. Onderstaande figuur laat zien dat groep AB’DE is samengesteld uit twee gestapelde cellen. Groep A'B'E bestaat uit twee gestapelde paren cellen.

Voor de A'B'E groep van 4-cellen ABCDE =00xx1 voor de groep. Dat wil zeggen dat A,B,E hetzelfde zijn 001 respectievelijk voor de groep. En, CD=xx dat wil zeggen dat het varieert, geen gemeenschappelijkheid in CD=xx voor de groep van 4-cellen. Sinds ABCDE =00xx1 , de groep van 4-cellen wordt gedekt door A'B'XXE =A'B'E .

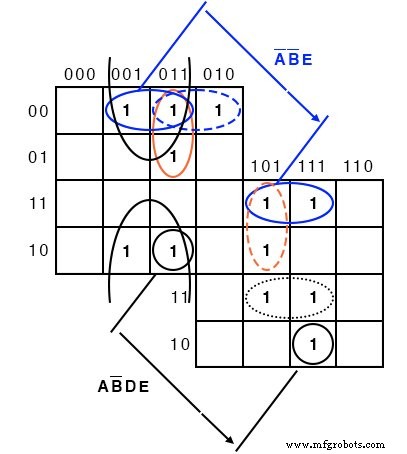
De bovenstaande 5-variabele overlay-kaart wordt gestapeld weergegeven.

Een voorbeeld van een Karnaugh-kaart met zes variabelen volgt. We hebben de vier subkaarten mentaal gestapeld om de groep van 4-cellen te zien die overeenkomt met Out =C'F'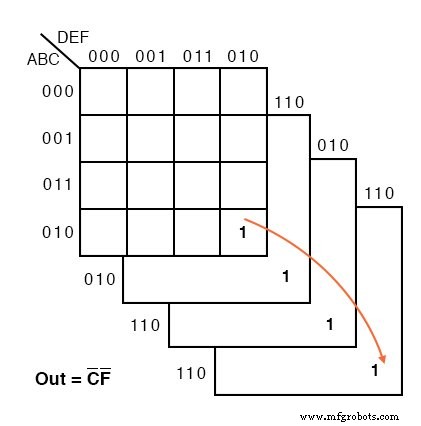

Een magnitudevergelijker (gebruikt om een ​​6-variabele K-map te illustreren) vergelijkt twee binaire getallen en geeft aan of ze gelijk, groter of kleiner zijn dan elkaar op drie respectieve uitgangen. Een drie bit magnitude comparator heeft twee ingangen A₂ A₁ A₀ en B₂ B₁ B₀ Een magnitude-comparator voor geïntegreerde circuits (7485) zou eigenlijk vier ingangen hebben, maar de onderstaande Karnaugh-kaart moet op een redelijke grootte worden gehouden. We lossen alleen de A>B . op uitvoer.

6 Variabele K-map

Hieronder helpt een Karnaugh-kaart met 6 variabelen om de logica voor een 3-bits magnitude-comparator te vereenvoudigen. Dit is een overlay-type kaart. De binaire adrescode bovenaan en onderaan de linkerkant van de kaart is geen volledige 3-bit grijze code.

Hoewel de 2-bits adrescodes van de vier subkaarten Gray-code zijn. Vind overtollige uitdrukkingen door de vier subkaarten op elkaar te stapelen (hierboven weergegeven). Er kunnen cellen zijn die alle vier de kaarten gemeen hebben, maar niet in het onderstaande voorbeeld. Het heeft cellen die gemeenschappelijk zijn voor paren van subkaarten.

De A>B-uitvoer hierboven is ABC>XYZ op de onderstaande kaart.

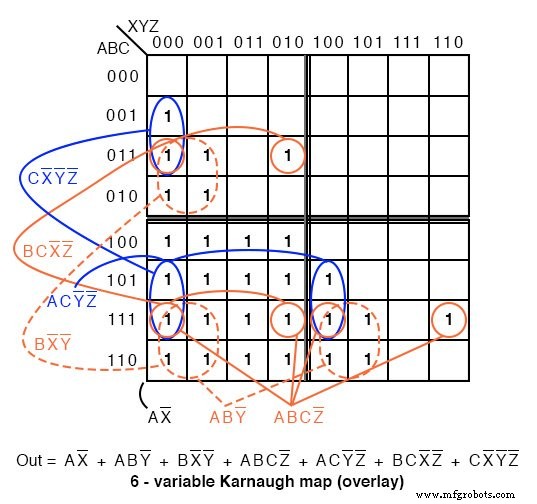
Waar ooit ABC is groter dan XYZ , een 1 wordt geplot. In de eerste regel ABC=000 kan niet groter zijn dan een van de waarden van XYZ . Nee 1 s in deze regel. In de tweede regel, ABC=001 , alleen de eerste cel ABCXYZ=001000 is ABC groter dan XYZ . Een enkele 1 wordt ingevoerd in de eerste cel van de tweede regel. De vierde regel, ABC=010 , heeft een paar 1 s. De derde regel, ABC=011 heeft drie 1 s. De kaart is dus gevuld met 1 s in cellen waar ABC is groter dan XXZ .

Vorm in het groeperen van cellen indien mogelijk groepen met aangrenzende subkaarten. Op één groep na zijn alle 16-cellen cellen van paren van de subkaarten. Zoek naar de volgende groepen:

• 1 groep van 16 cellen
• 2 groepen van 8 cellen
• 4 groepen van 4-cellen

De groep van 16 cellen, AX’ neemt de hele subkaart rechtsonder in beslag; we omcirkelen het echter niet in de bovenstaande afbeelding.

Een groep van 8 cellen bestaat uit een groep van 4 cellen in de bovenste subkaart die een vergelijkbare groep in de linkeronderkaart overlapt. De tweede groep van 8 cellen is samengesteld uit een vergelijkbare groep van 4 cellen in de rechter subkaart die dezelfde groep van 4 cellen in de linker benedenkaart overlapt.

De vier groepen van 4-cellen zijn weergegeven op de Karnaugh-kaart hierboven met de bijbehorende producttermen. Samen met de productvoorwaarden voor de twee groepen van 8 cellen en de groep van 16 cellen, wordt de uiteindelijke Sum-Of-Products-reductie weergegeven, alle zeven termen.

De 1 . tellen s op de kaart, zijn er in totaal 16+6+6=28 enen. Vóór de reductie van de K-map-logica zouden er 28 producttermen in onze SOP-uitvoer zijn geweest, elk met 6 ingangen. De Karnaugh-kaart leverde zeven producttermen van vier of minder inputs op. Dit is echt waar Karnaugh-kaarten over gaan!

Het bedradingsschema wordt niet getoond. Hier is echter de onderdelenlijst voor de 3-bit magnitude comparator voor ABC>XYZ met 4 TTL logische familie onderdelen:

• 1 ea 7410 drievoudige NAND-poort met 3 ingangen AX', ABY', BX'Y'
• 2 ea 7420 dubbele NAND-poort met 4 ingangen ABCZ', ACY'Z', BCX'Z', CX'Y'Z'
• 1 ea 7430 NAND-poort met 8 ingangen voor uitvoer van 7-P-termen

BEOORDELING:

• Booleaanse algebra, Karnaugh-kaarten en CAD (Computer Aided Design) zijn methoden voor logische vereenvoudiging. Het doel van logische vereenvoudiging is een oplossing met minimale kosten.
• Een oplossing met minimale kosten is een geldige logische reductie met het minimum aantal poorten met het minimum aantal ingangen.
• Venn-diagrammen stellen ons in staat om Booleaanse uitdrukkingen te visualiseren, waardoor de overgang naar Karnaugh-kaarten wordt vergemakkelijkt.
• Karnaugh-kaartcellen zijn gerangschikt in grijze codevolgorde, zodat we redundantie in Booleaanse uitdrukkingen kunnen visualiseren, wat resulteert in vereenvoudiging.
• De meer algemene Sum-Of-Products (Sum of Minters) uitdrukkingen worden geïmplementeerd als EN-poorten (producten) die een enkele OF-poort (som) voeden.
• Sum-Of-Products-expressies (AND-OR-logica) zijn equivalent aan een NAND-NAND-implementatie. Alle EN-poorten en OF-poorten worden vervangen door NAND-poorten.
• Minder vaak gebruikt, worden Product-Of-Sums-expressies geïmplementeerd als OF-poorten (sommen) die worden ingevoerd in een enkele EN-poort (product). Product-of-Sums-uitdrukkingen zijn gebaseerd op de 0 s, maxterms, in een Karnaugh-kaart.