Een biaxiale reksensor die een enkel MoS2-rooster gebruikt

Abstract

In dit artikel rapporteren we een nieuw type MoS₂ -gebaseerde roostersensor voor biaxiale rekstrookjes in het vlak met een precisielimiet van ~ 1‰. De MoS₂ rooster wordt numeriek gesimuleerd met verschillende biaxiale spanningen tot 5%. Onze eerste-principeberekeningen laten zien dat de spanningsgevoeligheid van de MoS₂ reflectiespectrum kan worden beschouwd als een extra spanningssensor die is geïntegreerd in de roosterstructuur, waardoor biaxiale spanningen in het vlak in kaart kunnen worden gebracht. Onze experimentele studies op een prototype MoS₂ -roostersensor bevestigt verder dat een spanningscomponent loodrecht op de roosterperiode intensiteitspiekverschuivingen kan veroorzaken in de eerste-orde diffractiepatronen van het rooster. Dit werk opent een nieuwe weg naar het meten van biaxiale rek in het vlak in een enkelvoudig roosterapparaat. Onze nieuwe aanpak is toepasbaar op andere materialen met een voorspelbare reflectierespons onder biaxiale spanningen en het vermogen om een tweedimensionale enkelkristallaag te vormen.

Inleiding

Flexibele elektronicatechnologie heeft veel aandacht gekregen van de academische en industriële gemeenschappen, maar het ontwerp en de toepassing van flexibele apparaten op micro- en nanoschaal is een uitdaging vanwege de moeilijkheden bij het monitoren van dynamische verplaatsing en vervorming [1,2,3,4,5]. De meeste conventionele rekdetectiemethoden op basis van weerstandsrekstrookjes vereisen een geminiaturiseerde sensorarray [4, 6, 7], die moeilijk te produceren is voor flexibele elektronische toepassingen. Op optica gebaseerde tweedimensionale (2D) rekdetectietechnieken, zoals spikkelinterferometrie, zijn superieur aan die gebaseerd op piëzoweerstand vanwege hun hogere precisie [8]. Hun meetstrategie voor beeldcorrelatie wordt echter uitgedaagd door de vereisten van complexe beeldverwerkingstechnologie [8,9,10]. Een reflectierooster kan een hoge resolutie bieden voor de rekmeting, maar mist de mogelijkheid om 2D-rek binnen een enkel apparaat te detecteren [11].

In de afgelopen jaren hebben 2D-materialen enorme onderzoeksinspanningen opgeleverd. Na de introductie van grafeem [12, 13], is de familie van 2D-materialen uitgebreid met veel nieuwe leden, zoals dubbel atomaire dunne zwarte fosfor [14], drievoudige atomaire dunne overgangsmetaal dichalcogeniden [15], viervoudige atomaire dunne groep-III metalen monochalcogeniden [16] en andere niet-gelaagde 2D-materialen [17]. Er zijn veel interessante eigenschappen in deze materialen gevonden, waardoor ze in de schijnwerpers van de materiaalkunde staan [18,19,20,21,22,23,24].

De overgangsmetaaldichalcogeniden vertonen uitstekende optische en mechanische eigenschappen [25,26,27]. Bijvoorbeeld MoS₂ kan tot 19,5% [26] biaxiale spanning verdragen, vergezeld van zijn reflectiemodulatie [28], en WSe₂ kan een opmerkelijke Berry-krommingsdipool en een niet-lineair Hall-effect laten zien via strain-engineering [29]. Het opnemen van de spanningsgevoeligheid van het reflectiespectrum van een materiaal in de functie van het reflectierooster kan een efficiënte manier zijn om spanningsmetingen uit te breiden tot biaxiale detectie binnen een enkel apparaat. Er zijn echter geen rapporten over de reflectieroosters in combinatie met door spanning geïnduceerde materiaalreflectiemodulatie voor 2D-rekdetectietoepassingen.

Hier stellen we een nieuw type in-plane biaxiale spanningsdetectietechniek voor, waarbij de spanningsgevoeligheid van MoS₂ betrokken is. reflectie in een reflectieroostersensor. Eerste-principeberekeningen laten zien dat biaxiale spanningen de piek van de intensiteitsverdeling in diffractiepatronen van een MoS₂ kunnen verschuiven -gebaseerd roosterapparaat omdat de reflectie van MoS₂ is gevoelig voor de door rek veroorzaakte vervorming. Deze niet-lineaire piekverschuiving wordt goed gedemonstreerd door een tweede-orde term toe te voegen aan de uniaxiale-rek lineaire vergelijking, waaruit de rekcomponent loodrecht op de roosterperioderichting kan worden geëxtraheerd met een precisielimiet van ~ 1‰. Onze experimentele studies op een prototype MoS₂ -roosterapparaat bevestigt dat de rek loodrecht op de roosterperiode een intensiteitspiekverschuiving van het eerste-orde diffractiepatroon van het rooster kan veroorzaken. Ons onderzoek toont de mogelijkheid aan van one-shot, in-plane biaxiale rekstrookjes met een enkele roostersensor.

Methoden

Theoretische berekeningen voor MoS₂ Vlok

De MoS₂ optische reacties op de stam worden allemaal bestudeerd door eerste-principe berekeningen uitgevoerd met het Vienna Ab-initio Simulation Package (VASP) [30]. All-electron projector augmented wave (PAW) potentialen [31] werden gebruikt voor alle berekeningen. Geometrische relaxatie en statische berekeningen werden uitgevoerd met de Perdew-Burke-Ernzerhof (PBE) gegeneraliseerde gradiëntbenadering (GGA) methode [32]. Spin-orbitkoppeling (SOC) [33] werd ook meegenomen in de statische berekeningen. Om de optische eigenschappen te bepalen, werden eerst quasideeltjesenergieën verkregen met de GW-methode afgeleid van de groene functietheorie [34]. De golffunctie verkregen uit de statische berekeningen en de quasideeltjesenergie uit de GW-berekeningen werden gebruikt om de Bethe-Salpeter vergelijking (BSE) berekeningen [35] uit te voeren om de diëlektrische constante te voorspellen.

Een bulkkristalmodel werd gebruikt om de MoS₂ . weer te geven vlok (dat de verschillen in optische eigenschappen tussen stapels groter dan vijf lagen verwaarloosbaar zijn [36]). In de optimalisatieberekeningen werd de energiegrenswaarde ingesteld op 400 eV en werd een Monkhorst-Pack k-puntset van 15 * 15 * 4 gebruikt om de Brillouin-zone te bemonsteren. De roosterparameters werden eerst geoptimaliseerd als referentie voor latere berekeningen van de gespannen MoS₂ vlok. De geoptimaliseerde roosterparameters waren a = b = 3.18 Å en c = 13,87 Å. De geometrie was ontspannen totdat de energie convergeerde naar 10^–5 eV. Gebruikmakend van een techniek uit eerdere literatuur [37], een energiegrenswaarde van 300 eV en k -point set van 6 × 6 × 2 werden gebruikt in de optische berekeningen. De statische energie convergeerde naar 10^–6 eV in alle berekeningen. De diffractiepatronen werden gesimuleerd op basis van de stelling van Helmholtz-Kirchhoff [38]. Meer details vindt u in het aanvullende bestand 1.

Voorbereiding van MoS₂ Voorbeeld voor spectrummeting

Voorbereiding van MoS₂ Raspen op het flexibele substraat

De MoS₂ dunne film werd mechanisch geëxfolieerd van een commerciële MoS₂ single crystal (SPI Supplies) en overgebracht naar een polydimethylsiloxaan (PDMS) substraat met tape. Om het roosterapparaat te fabriceren, moet de MoS₂ vlok werd eerst in een roosterstructuur gemodelleerd door elektronenstraallithografie (EBL). Vervolgens werd het patroonmonster geëtst door zuurstofplasma met een vermogen van 20 W. Uiteindelijk verkregen we de MoS₂ -gebaseerd raspapparaat door het PMMA weg te spoelen.

MoS₂ Apparaatmetingen

Een supercontinuüm witte lichtbron (NKT Photonics SuperK Compact) wordt gebruikt als de excitatielaser, die door één opening gaat en het vlokmonster of het roostermonster onder een bepaalde hoek ten opzichte van het monstervlak raakt, zoals weergegeven in Fig. 1. In de reflectiemeting, wordt de gereflecteerde laser verzameld via een optische vezel die is aangesloten op een spectrometer. De reflectiespectra onder verschillende spanningen worden berekend uit de gegevens gemeten door de spectrometer. De MoS₂ . testen rooster wordt de gereflecteerde laser geprojecteerd op een wit bord en verschijnt als een lange elliptische lichtvlek. Foto's van de lichtvlek worden gebruikt om de intensiteitsverdeling te analyseren.

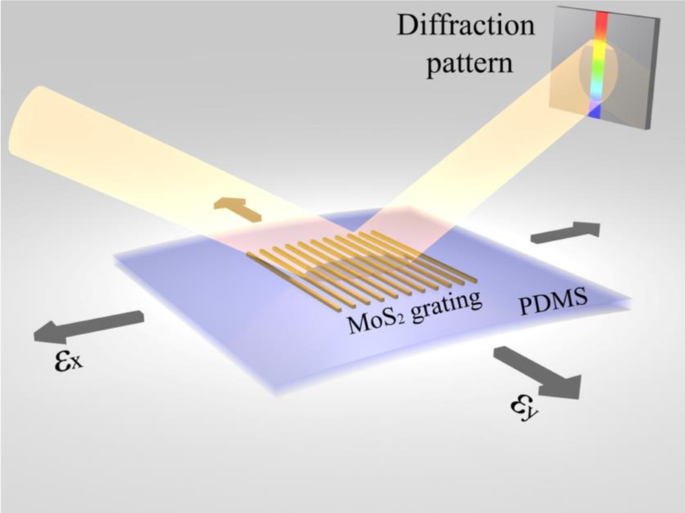
Schematische illustratie van MoS₂ -gebaseerde roostersensor op een flexibel substraat van PDMS voor biaxiale rekstrookjes

Resultaten en discussie

In een conventionele reflectieroostersensor kan een periodieke structuur van parallelle roosterstroken het licht afbuigen, en de diffractie wordt gebruikt om een spanning te meten die langs de richting van de roosterperiode loopt door een locatieverschuiving van de diffractiepatronen [11] te volgen. Vanwege de oriëntatie van de periodieke structuur is de rekdetectiefunctie van het reflectierooster beperkt tot de uniaxiale rekstrook in het vlak (parallel aan de periodieke richting). Om de reflectieroosterfunctie uit te breiden voor gebruik in biaxiale rekstrookjes in het vlak, stellen we voor dat de intrinsieke optische eigenschappen van het roostermateriaal, zoals de spanningsgevoeligheid van de reflectie van het materiaal, kunnen worden beschouwd als een extra spanningssensor om te detecteren in -vlak rekcomponenten loodrecht op de periodieke richting.

MoS₂ heeft een gelaagde structuur:een laag Mo-atomen ingeklemd tussen twee lagen S-atomen. De interactie tussen de lagen is een zwakke van der Waalskracht. Hier ontwerpen we een MoS₂ op vlokjes gebaseerde reflectieroostersensor (Fig. 1) en onderzoek de diffractiepatronen van het apparaat onder verschillende biaxiale spanningen in het vlak door eerste-principeberekeningen. Het golflengtebereik van de invallende bundel in onze berekening is van 400 tot 850 nm. Het diffractierooster kan worden beschreven door:

$$d\left(\mathrm{sin}{\theta }_{i}-\mathrm{sin}{\theta }_{m}\right)=n\lambda$$ (1)

waarbij $d$ de afstand is tussen twee aangrenzende traliestroken, ${\theta }_{i}$ de hoek is tussen de invallende bundel en de normaal op het tralie, ${\theta }_{m }$ is de hoek tussen de diffractiestraal en de normaal wanneer de diffractiestraal maxima heeft, n is de diffractievolgorde, en $\lambda$ is de bundelgolflengte [11]. Van verg. (1) zien we dat invallende stralen met verschillende $\lambda$ verschillende ${\theta }_{m}$ moeten hebben. Daarom veroorzaakt een continue golflengtebundel een continue reeks diffractievlekken die overeenkomen met verschillende ${\theta }_{m}$, waardoor een elliptisch eerste-orde diffractiepatroon wordt gevormd.

Afbeelding 2a toont het gesimuleerde beeld van de diffractiepatronen van de als ontworpen roostersensor zonder dat er spanning wordt uitgeoefend. Figuur 2b toont de evolutie van de intensiteitspiek en patroonlocatie van het gesimuleerde eerste-orde diffractiepatroon van het apparaat onder verschillende biaxiale spanningen. De rand van het diffractiepatroon van de eerste orde die overeenkomt met de invallende bundel van 850 nm, wordt aangeduid met "LW". Wanneer we een uniaxiale trekspanning in het vlak toepassen langs de richting van de roosterperiode (${\varepsilon }_{x}$), kan deze spanning een toename van de afstand d veroorzaken tussen elke strook. Als resultaat wordt ${\theta }_{m}$ kleiner omdat $d\mathrm{sin}{\theta }_{m}$ constant is voor een gegeven $\lambda$ en vast \ ({\theta }_{i}\). Daarom, wanneer we de spanning ${\varepsilon }_{x}$ geleidelijk verhogen van 0 naar 4,3%, beweegt de locatie van elk punt in het eerste-orde diffractiepatroon dichter naar het midden van de nulde-orde diffractievlek in een proportionele relatie met de corresponderende bundelgolflengte, wat consistent is met de functie van de conventionele reflectieroostersensor [11].

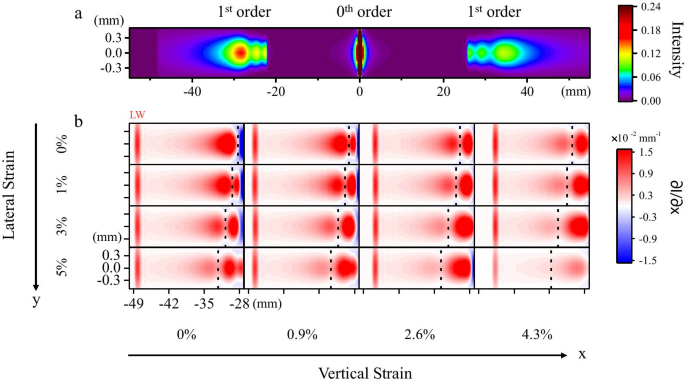
een Gesimuleerd beeld van het diffractiepatroon. Er werd geen spanning toegepast. De intensiteit wordt weergegeven met kleuren. Er is asymmetrisch gedrag tussen de eerste-orde diffractievlek aan beide zijden van de nulde-orde bundel omdat het scherm in onze simulatie is ingesteld om evenwijdig aan het rooster te zijn in plaats van loodrecht op de reflectierichting. b Gesimuleerde evolutie van eerste-orde diffractievlek onder verschillende biaxiale spanningen. Het gedeeltelijke intensiteitsverschil wordt weergegeven met kleuren. De horizontale coördinaat en verticale coördinaat geven de positie aan ten opzichte van het midden van de nulde-orde diffractievlek. De piek is gemarkeerd met een stippellijn. Van links naar rechts is ${\varepsilon }_{x}$ ingesteld op respectievelijk 0%, 0,9%, 2,6% en 4,3%. Van boven naar beneden was de ${\varepsilon }_{y}$ respectievelijk 0%, 1%, 3% en 5%

Een invallende bundel met een langere golflengte $\lambda$ heeft een grotere ${\theta }_{m}$ variatie, dus de LW-rand heeft de meest duidelijke locatieverschuiving. Wanneer echter tegelijkertijd een in-plane trekspanning loodrecht op de roosterperioderichting (${\varepsilon }_{y}$) wordt toegepast, wordt een intensiteitpiekverschuiving waargenomen binnen het eerste-orde diffractiepatroon, zoals aangegeven door een stippellijn in figuur 2b. Wanneer de rek ${\varepsilon }_{y}$ toeneemt van 0 tot 5%, verschuift de intensiteitspiek verder weg van het centrum van de nulde-orde diffractievlek. We schrijven deze piekverschuiving van de intensiteitsverdeling toe aan de spanning-geïnduceerde modulatie van de MoS₂ reflectie. Eerdere literatuur heeft gemeld dat het reflectiespectrum van MoS₂ kan worden afgestemd door een externe spanning [28], en de reflectie is gelijk aan de intensiteitsverhouding van de afgebogen bundel tot de invallende bundel van het reflectierooster. Daarom is de intensiteit van de bundels met verschillende golflengten afgebogen door de MoS₂ rooster kan worden gemoduleerd door de spanningen in het vlak. Ondertussen vindt er geen LW-randlocatieverschuiving plaats omdat de rek ${\varepsilon }_{y}$ geen invloed heeft op de roosterperiode.

Afbeelding 3a toont het lineaire gedrag in de piekverschuivingen van de MoS₂ reflectiespectra bij een uniaxiale trekspanning langs de roostervector ${\varvec{b}}$ van MoS₂ is toegepast. Deze uniaxiale trekspanning veroorzaakt een piek-positie roodverschuiving in de MoS₂ reflectie. Er is echter een niet-lineaire modulatie in de reflectiepiekpositieverschuiving wanneer we een biaxiale trekspanning in het vlak toepassen. De relatie tussen de piekpositie in de reflectiespectra en de biaxiale trekrek in het vlak kan worden beschreven met een tweede-ordevergelijking:

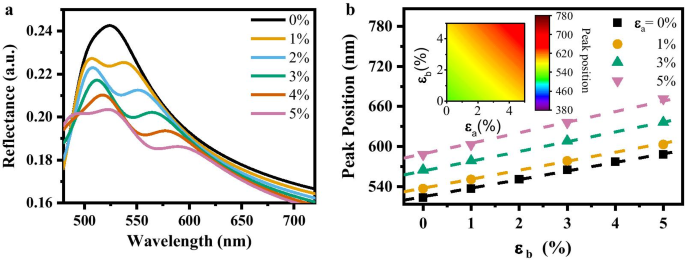
een Reflectiespectra van de MoS₂ vlok als functie van de golflengte onder verschillende uniaxiale spanningen. b Piekposities van de reflectiespectra van de MoS₂ schilferen onder verschillende biaxiale spanningen. Stippellijnen vertegenwoordigen de passende curven. Inzet:het afbeeldingsbeeld van piekposities uit de aanpassingsvergelijking

$$\mathrm{Piekpositie}=l\left({\varepsilon }_{a}+{\varepsilon }_{b}\right)+m{\varepsilon }_{a}{\varepsilon }_{b }+n$$ (2)

waar l , m , en n zijn drie constanten, en ε _een en ε _b zijn de stamcomponenten langs de twee roostervectoren van de MoS₂ . De eerste term beschrijft het lineaire gedrag van de piekpositieverschuiving onder uniaxiale trekspanningen langs roostervector ${\varvec{a}}$ of ${\varvec{b}}$. De tweede term beschrijft het gedrag van hogere orde in de biaxiale trekspanningssituatie. De derde term is de reflectiepiekpositie van de ongespannen MoS₂ . Sinds de MoS₂ roostervectoren ${\varvec{a}}$ en ${\varvec{b}}$ zijn symmetrisch equivalent, de trekspanningen langs de twee richtingen hebben dezelfde bijdragefactor. De fittingresultaten laten zien dat het grootste verschil tussen de fittingcurve en de volgens het eerste principe berekende piekposities 1,76 nm is, wat aangeeft dat een rekstrookprecisielimiet van ~ 1‰ kan worden verkregen wanneer de reflectiepiekpositie wordt gebruikt om te berekenen de stam met de Eq. (2). Figuur 3b toont het afbeeldingsbeeld van de reflectiepiekpositie onder verschillende biaxiale trekspanningen in het vlak verkregen uit de gemonteerde vergelijking. (2) (zie gedetailleerde grafieken van reflectie in Aanvullend bestand 1).

In onze simulatie staat de roostervector ${\varvec{a}}$ loodrecht op de perioderichting van het gesimuleerde rooster. Daarom is de stam ${\varepsilon }_{y}$ gelijk aan ${\varepsilon }_{a}$, en is stam ${\varepsilon }_{x}$ gelijk aan $\ sqrt{3}/2\times {\varepsilon }_{b}$. Uit onze berekeningen blijkt dat in een MoS₂ -gebaseerde roostersensor, kan de rek in het vlak ${\varepsilon }_{x}$ worden gemeten door de LW-randlocatieverschuiving van het eerste-orde diffractiepatroon. Op basis van de intensiteitspiekverschuiving in het eerste-orde diffractiepatroon, kunnen we de tweede-orde Eq gebruiken. (2) om de bijdrage van de in-plane strain ${\varepsilon }_{x}$ af te trekken van de piekverschuiving. Dan kunnen we de in-plane strain ${\varepsilon }_{y}$ kwantitatief berekenen.

Om de spanningsgevoeligheid van de MoS₂ . verder experimenteel te bestuderen reflectie, hebben we een MoS₂ . mechanisch geëxfolieerd vlok (dikte van enkele tientallen nanometers; zie details in aanvullend bestand 1) en bevestigde de vlok op een flexibel substraat van polydimethylsiloxaan (PDMS) door middel van een droge overdrachtsmethode (getoond in inzet van figuur 4a). Op deze gefabriceerde MoS₂ . werd een uniaxiale trekspanning in het vlak opgelegd apparaat door de twee zijden van het substraat aan twee translatiestadia te bevestigen en het substraat uit te rekken. We hebben de uniaxiale trekrek in het vlak geschat door ε . te berekenen $=\delta L/L$, waarbij $L$ de lengte van het substraat tussen de twee clips is en $\delta L$ de lengteverandering is. Wanneer de rek wordt gevarieerd van 0 tot 4%, is er een roodverschuiving van de piekpositie in de MoS₂ reflectiespectrum, en de grootte van deze verschuiving komt goed overeen met onze theoretische berekeningen, zoals weergegeven in figuur 4a. Figuur 4b, c toont het optische beeld van een op MoS2 gebaseerde reflectieroostersensor met een periode van 2 μm op een PDMS flexibel substraat vervaardigd door elektronenstraallithografie (details in Methoden). Bij het uitrekken van het PDMS-substraat wordt een trekspanning in het vlak loodrecht op de perioderichting uitgeoefend op de MoS₂ -gebaseerd roosterapparaat (Fig. 4d). Door de intensiteitsverdeling in het eerste-orde diffractiepatroon te volgen, hebben we waargenomen dat de intensiteitspiek verder van het midden van de nulde-orde-vlek verschuift in vergelijking met het niet-gespannen geval wanneer we een in-plane trekspanning van 4% loodrecht op de perioderichting (Fig. 4e). Er wordt geen locatieverschuiving van het diffractiepatroon verkregen omdat de trekspanning loodrecht staat op de perioderichting en de afstand d tussen elke strip verandert weinig.

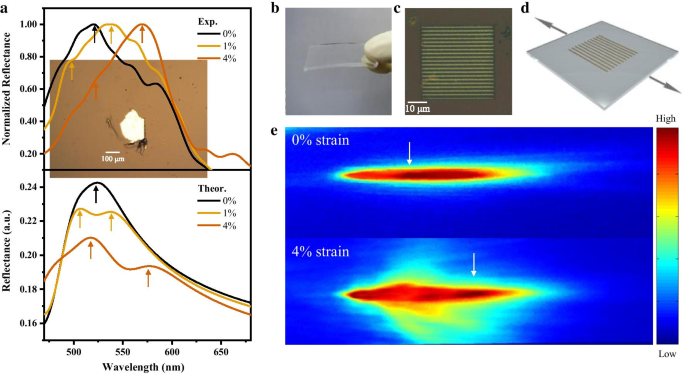
een Experimentele resultaten van reflectiespectra met uniaxiale rekken (boven), en de eerste principes berekenden reflectiespectrum met uniaxiale rekken (onder). Pijlen geven de pieklocaties van de reflectie aan. Inzet, optische afbeelding van de MoS₂ vlok gebruikt voor het testen van het reflectiespectrum. b –c Optische beelden van de gefabriceerde MoS₂ -gebaseerd rooster op PDMS. d Schematisch diagram van MoS₂ -gebaseerd rooster uitgerekt door vertaalstadia. e Afbeelding van de eerste-orde diffractievlek van het ongespannen (boven) en het gespannen (onder) rooster. Witte pijlen geven de intensiteitspiek aan

Conclusie

Samenvattend demonstreren we een nieuwe techniek voor het meten van biaxiale rek in het vlak met behulp van een MoS₂ -gebaseerde reflectieroostersensor. We testen het concept door het rooster numeriek te simuleren met verschillende biaxiale rekken tot 5%. In deze nieuwe techniek wordt de roosterstructuur voor het detecteren van de rekcomponent langs de perioderichting (${\varepsilon }_{x}$) gecombineerd met de rekgevoeligheid van de MoS₂ reflectie om als een extra sensor te fungeren om de in-plane rekcomponent loodrecht op de perioderichting te verkrijgen (${\varepsilon }_{y}$). Component ${\varepsilon }_{y}$ wordt berekend met een tweede-orde benaderingsvergelijking en de intensiteitspiekverschuiving binnen de eerste-orde diffractiepatronen. De theoretische resultaten worden goed ondersteund door onze experimenten. Ons werk opent een weg voor het ontwerp van flexibele roostersensoren en biedt een nieuwe benadering om one-shot biaxiale rekstrookjes in het vlak te realiseren met een enkele roostersensor. Onze aanpak is ook toepasbaar op andere materialen die een voorspelbare reflectierespons hebben onder biaxiale spanningen en het vermogen hebben om tweedimensionale eenkristallagen te vormen.