Twee technieken om resistieve sensorbruggen te lineariseren

Het meten van de minuscule weerstandsveranderingen in resistieve sensoren kan een ontmoedigende taak zijn. Hier zijn twee hardwaremethoden om niet-lineariteitsfouten te elimineren.

De weerstand van een resistieve sensor hangt af van een fysieke variabele zoals temperatuur of kracht. De procentuele verandering in de weerstand van deze apparaten is meestal klein. De totale verandering in de weerstand van een rekstrookje kan bijvoorbeeld minder dan 1% zijn over het gehele werkbereik.

Het onderscheiden van deze kleine waarden vereist zeer nauwkeurige meetcircuits. Brugcircuits stellen ons in staat om deze nauwkeurige metingen gemakkelijker uit te voeren. De uitvoer van een brugschakeling kan echter een niet-lineaire relatie hebben met de gemeten fysieke variabele, zelfs als we een lineaire sensor gebruiken.

In deze gevallen kunnen we software- of hardwaretechnieken gebruiken om de niet-lineariteitsfouten van de brug te elimineren. In dit artikel bekijken we twee verschillende technieken voor het lineariseren van resistieve sensorbruggen.

Overbrug niet-lineariteit van resistieve sensoren

Overweeg een resistieve druksensor met de volgende lineaire respons:

\[R_{sensor} =R_0 + Mx\]

waar R₀ is de initiële weerstand van de sensor bij nuldruk, x is de waarde van de meetgrootheid (druk) en M is de helling van de sensorrespons. Laten we, om onze toekomstige vergelijkingen eenvoudiger te maken, aannemen dat de waarde van M gelijk is aan de waarde van de initiële weerstand van de sensor (R₀ ) en daarom is de sensorrespons \[R_0(1+x)\].

Gewoonlijk is de procentuele verandering in de weerstand van een resistieve sensor klein en moeten we een brugschakeling gebruiken om gemakkelijker nauwkeurige metingen uit te voeren. Een algemene brugconfiguratie voor deze sensor wordt weergegeven in afbeelding 1.

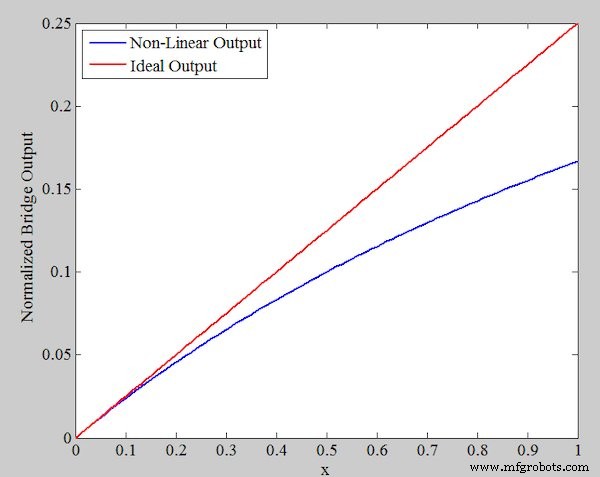
Figuur 1. Gemeenschappelijke brugconfiguratie van een resistieve sensor

Merk op dat de andere drie weerstanden van de brug een weerstand hebben van R₀ . Deze keuze van brugweerstanden maximaliseert de gevoeligheid van de uitgang (V_out ) op veranderingen in de sensorweerstand. De uitvoervergelijking kan worden verkregen als:

\[V_{out} =V_A - V_B =V_r\left(\frac{R_0(1+x)}{R_0+R_0(1+x)} - \frac {1}{2}\right)\]

Dit vereenvoudigt tot:

\[V_{out} =V_r\left(\frac{x}{2(2+x)}\right)\]

Vergelijking 1.

Zoals u kunt zien, is de relatie tussen de bruguitgang en de verandering in de weerstandswaarde (x) niet lineair. Met \[x\ll2\] kunnen we de bovenstaande vergelijking benaderen door de volgende lineaire relatie:

\[V_{out} \circa V_r\left(\frac{x}{4}\right)\]

Vergelijking 2.

Figuur 2 toont de genormaliseerde output van de brug \[\frac{V_{out}}{V_r}\] voor zowel het werkelijke geval (vergelijking 1) als de ideale output (vergelijking 2).

Figuur 2. Niet-lineaire (blauw) en ideale (rode) uitvoer van vergelijkingen 1 en 2

Zoals verwacht neemt de afwijking van de lineaire respons toe met x.

Hoeveel niet-lineariteitsfout zal worden geïntroduceerd?

Laten we de niet-lineariteitsfout van het bovenstaande brugcircuit kwantificeren. We kunnen vergelijking 1 herschrijven als:

\[V_{out} =V_r \left(\frac{x}{4}\right) \left(\frac{1}{1+ \frac{x} {2}}\right)\]

Ervan uitgaande dat \[\frac{x}{2} <<1\], we kunnen de stelling van Taylor gebruiken om een ​​benadering van de bovenstaande functie te verkrijgen als:

\[V_{out} =V_r\left(\frac{x}{4}\right)\left(1 - \frac{x}{2}\right) \]

Als we dit resultaat vergelijken met vergelijking 2, kunnen we de grootte van de fout als volgt berekenen:

\[E_{Non-Linearity} =V_r\left(\frac{x}{4}\right)\left(\frac{x}{2}\right) \]

Door dit te delen door de verwachte ideale waarde gegeven door vergelijking 2, kunnen we de procentuele eindpunt-lineariteitsfout verkrijgen voor een gegeven verandering in weerstand (x):

\[Percentage~Error =\frac{x}{2} \times 100\%\]

Voorbeeld van het berekenen van de niet-lineariteitsfout

Beschouw een sensor met respons \[R_{sensor} =R_0(1+x)\]. Neem aan dat \[R_0 =100~\Omega\] en de maximale waarde van x over het gehele werkbereik 0,01 is. Het maximale lineariteitsfoutpercentage is:

\[Percentage~Error =\left(\frac{0.01}{2}\right) \times 100\% =0.5\%\]

Merk op dat hoewel we misschien software kunnen gebruiken om de sensorlineariteitsfouten te verwijderen, een lineaire respons wenselijk is omdat dit de meetnauwkeurigheid verhoogt en systeemkalibratie vergemakkelijkt. Er zijn verschillende circuittopologieën die kunnen worden gebruikt om brugcircuits te lineariseren.

In de rest van dit artikel zullen we twee verschillende bruglinearisatietechnieken onderzoeken.

Methode 1:Een spanning creëren die evenredig is aan weerstandsveranderingen (x)

De eerste linearisatietechniek die we in dit artikel zullen bespreken, wordt getoond in figuur 3. Laten we eerst het basisidee van deze techniek onderzoeken en dan kijken hoe het circuit in figuur 3 dit idee implementeert.

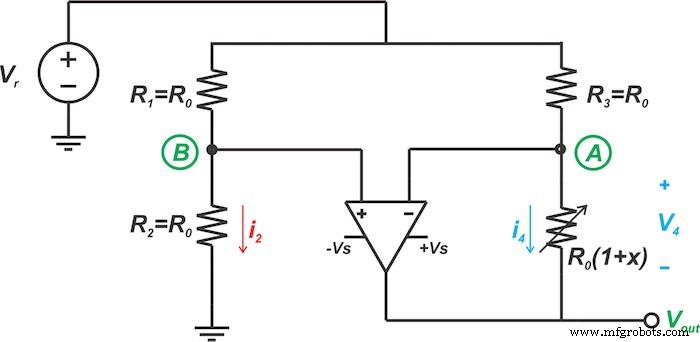
Figuur 3. Eén type circuit voor het lineariseren van resistieve sensorbruggen

Figuur 4 toont een afbeelding van een vaste stroom van \[I_{Ref}\] gedwongen om door onze lineaire sensor te stromen.

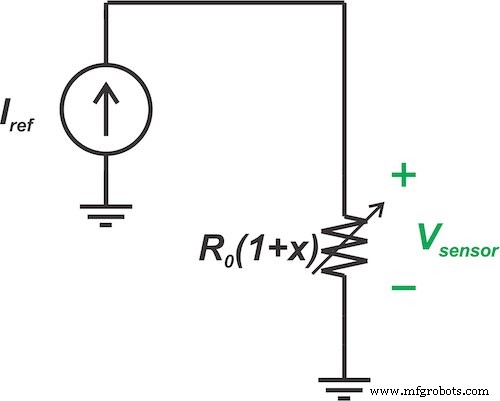
Figuur 4. Een vaste stroom (I_Ref ) gedwongen door een lineaire sensor

In dit scenario zou de resulterende spanning over de sensor zijn:

\[V_{sensor} =I_{Ref} \times R_0(1 + x)\]

die kan worden herschikt als:

\[V_{sensor} =R_0 \times I_{Ref} + R_0 \times I_{Ref} \times x\]

Terwijl de eerste term een ​​constante waarde is, is de tweede term evenredig met de veranderingen in de sensorweerstand (x). Als we de constante term kunnen weglaten, hebben we een spanning die een lineaire relatie heeft met x.

Circuitimplementatie

Het circuit in figuur 3 gebruikt het bovenstaande idee om het brugcircuit te lineariseren. Aangezien de op-amp-ingangen idealiter geen stroom trekken, zal de spanning op knooppunt B een constante waarde hebben van:

\[v_B =\frac{R_0}{R_0 + R_0}V_r =\frac{V_r}{2}\]

De negatieve feedback en de hoge versterking van de op-amp zorgen ervoor dat zowel de inverterende als de niet-inverterende ingangen van de op-amp dezelfde spanning hebben:

\[v_A =v_B =\frac{V_r}{2}\]

Aangezien beide uiteinden van R3 op constante potentialen staan, zal er een constante stroom doorheen vloeien. Met andere woorden, de op-amp zorgt ervoor dat R3 werkt als een stroombron die een constante stroom van \[\frac{V_r}{2R_0}\] in de sensor dwingt. De spanning over de sensor zal dus zijn:

\[V_4 =\frac{V_r}{2R_0} \times R_0(1 + x) =\frac{V_r}{2} + \frac{V_r}{2} x\]

De eerste term is de constante waarde die moet worden geëlimineerd uit de V_out vergelijking. De tweede term is evenredig met de veranderingen in de sensorweerstand (x) en zou in de uitgangsvergelijking moeten verschijnen. Als we de spanningswet van Kirchhoff toepassen, vinden we V_out als:

\[V_{out} =-V_4 + V_A =- \left(\frac{V_r}{2} + \frac{V_r}{2}x\right) + V_A\]

Daarom hebben we alleen V_A . nodig gelijk zijn aan \[\frac{V_r}{2}\]. Hieraan is al voldaan, wat leidt tot:

\[V_{out} =-\frac{V_r}{2}x\]

Daarom heeft de uitvoer een lineaire relatie met x.

Methode 2:Een stroom creëren die evenredig is aan weerstandsveranderingen (x)

De tweede bruglinearisatietechniek die we in dit artikel zullen bespreken, wordt getoond in figuur 5.

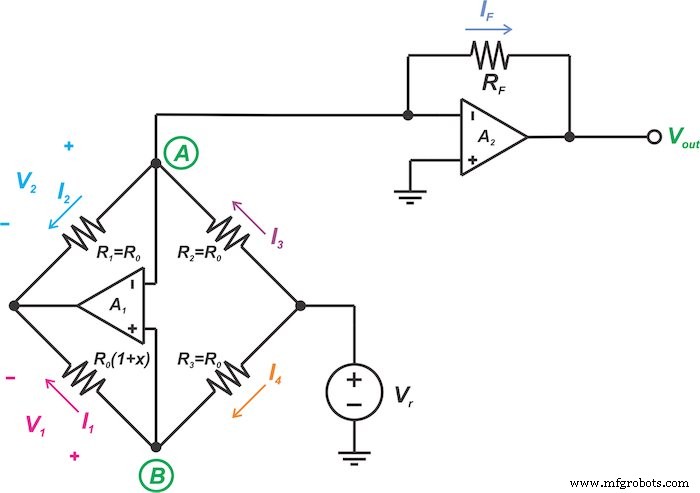
Figuur 5. Een ander circuit voor de analoge linearisatie van resistieve sensorbruggen

Laten we nog eens kijken naar het basisidee van deze techniek en dan de implementatie van het circuit onderzoeken.

Deze tweede linearisatietechniek wordt geïllustreerd in figuur 6.

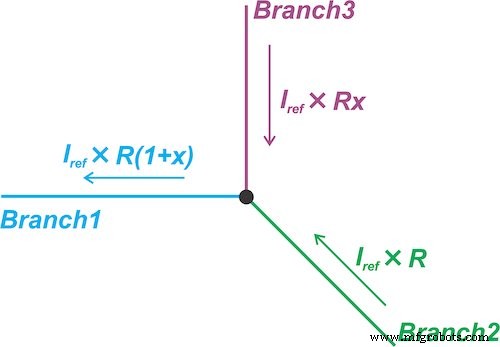
Figuur 6. Linearisatietechniek die de stroom door een tak van het circuit dwingt om evenredig te zijn met de weerstand van de sensor

Het dwingt de stroom door een tak van het circuit (tak 1) om evenredig te zijn met de sensorweerstand:

\[I_1 =I_{Ref} \times R_0(1 + x)\]

waar ik_Ref is een constante waarde. Vervolgens voert het de huidige domeinaftrekking uit om de constante term \[I_{Ref} \times R_0\] te elimineren. Hiertoe wordt de stroom door Tak 2 ingesteld op \[I_{Ref} \times R_0\]. De stroom door Tak 3 is dus \[I_{Ref} \times R_0x\]— evenredig met de veranderingen in de sensorweerstand (x).

Circuitimplementatie

Laten we eens kijken hoe het circuit in figuur 5 het bovenstaande idee implementeert. Nogmaals, de negatieve feedback en de hoge versterking van de op-amps zullen zowel de inverterende als niet-inverterende ingangen van de twee op-amps (beide A₁ en A₂ ) om dezelfde spanning te hebben:

\[v_A =v_B =0\]

Vergelijking 3.

Daarom hebben we V₁ =V₂ dat leidt tot

\[R_0 (1 + x) \times I_1 =R_0 \times I_2\]

Dit vereenvoudigt tot:

\[I_2 =I_1 + I_1 \times x\]

Vergelijking 4.

We weten dat I₁ =I₄ en, rekening houdend met vergelijking 3, hebben we:

\[I_1 =I_4 =\frac{V_r - v_A}{R_0} =\frac{V_r}{R_0}\]

Als we dit in vergelijking 4 invullen, krijgen we:

\[I_2 =\frac{V_r}{R_0} + \frac{V_r}{R_0} \times x\]

Vandaar, I₂ is de som van een constante waarde en een term die evenredig is met x. We hoeven alleen de huidige wet van Kirchhoff te gebruiken om de constante term in de uitgangsstroomvergelijking te elimineren. De stroom door R2 levert een stroom gelijk aan \[\frac{V_r}{R_0}\] naar knoop A, wat leidt tot:

\[I_F =-\frac{V_r}{R_0} \times x\]

Daarom verkrijgen we:

\[V_{out} =V_r \times \frac{R_F}{R_0} \times x\]

Het circuit in figuur 5 heeft een extra op-amp nodig in vergelijking met de eerste techniek. Met de twee op-amp-oplossingen kunnen we de versterking echter willekeurig instellen door de verhouding \[\frac{R_F}{R_0}\] te kiezen.

Ga naar deze pagina om een ​​volledige lijst van mijn artikelen te zien.