SUPERMESH Circuitanalyse | Stap voor stap met opgelost voorbeeld

Supermesh  Analyse – Verklaring , formule, opgeloste voorbeelden

Wat is Supermesh-analyse?

Supermesh- of Supermesh-analyse is een betere techniek in plaats van Mesh-analyse om zo'n complex elektrisch circuit of netwerk te analyseren, waarbij twee mazen een stroombron als gemeenschappelijk element hebben. Dit is hetzelfde waar we Supernode-circuitanalyse . gebruiken in plaats van Node- of Nodal-circuitanalyse om een ​​dergelijk netwerk te vereenvoudigen waarbij de supernode wordt toegewezen, waarbij de spanningsbron volledig wordt ingesloten in de supernode en het aantal niet-referentieknooppunten wordt verminderd met één (1) voor elke spanningsbron.

In de supermesh-circuitanalysetechniek bevindt de stroombron zich in het binnengebied van de supermesh. Daarom zijn we in staat om het aantal mazen met één (1) te verminderen voor elke stroombron die in het circuit aanwezig is.

De enkele mesh kan worden genegeerd, als de huidige bron (in die mesh) aan de rand van het circuit ligt. Als alternatief wordt KVL (Kirchhoff's Voltage Law) alleen toegepast op die meshes of supermeshes in het vernieuwde circuit.

Trouwens, het is moeilijk te begrijpen door Preamble, dus we zullen eerst een eenvoudig circuit oplossen door supermesh-circuitanalyses, en dan zullen we de hele supermesh-analyse samenvatten (stap per stap).

• Gerelateerde post:SUPERNODE-circuitanalyse | Stap voor stap met opgelost voorbeeld

Opgelost voorbeeld van Supermesh-analyse

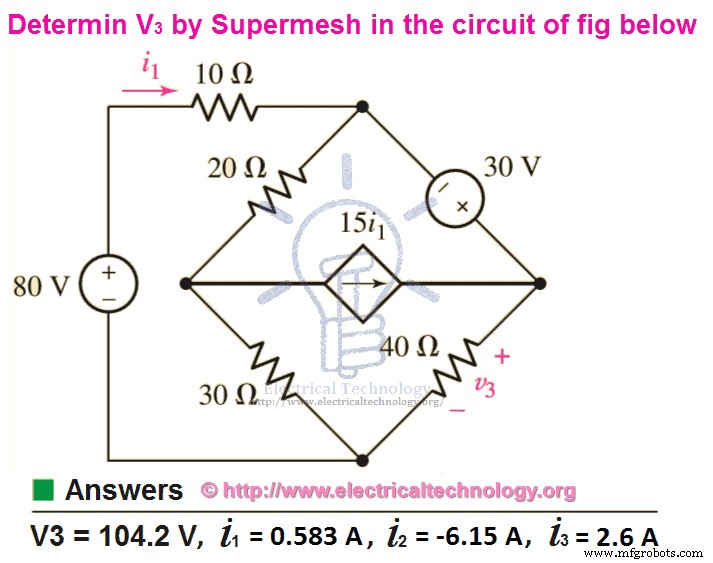
Voorbeeld:

Gebruik mesh-analyse om V₃ . te vinden en huidige i ₁ , ik ₂ en ik ₃ in de volgende afbeelding?

Oplossing:

KVA gebruiken op Mesh 1.

80 =10i ₁ + 20(ik ₁ –  ik ₂ ) + 30 (i ₁ – i₃ )

Vereenvoudigen

80 =10i ₁ + 20ik ₁ –  20ik ₂ + 30ik ₁ – 30ik ₃

80 =60i ₁ – 20ik ₂ –  30ik ₃ ….. → Vgl 1.

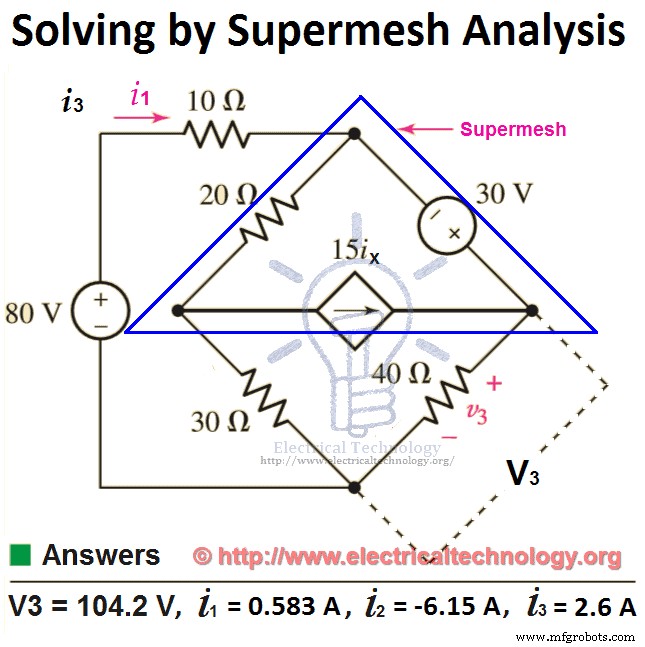
Toepassen KVL op Supermesh (dit is de integratie van mesh 2 en mesh 3 , maar we hebben het verkleind met een enkele mesh die bekend staat als supermesh )

30 =40i ₃ + 30(ik ₃ – ik ₁ ) +20(ik ₂ – ik ₁ )

30 =40i ₃ + 30ik ₃ – 30ik ₁ + 20ik ₂ – 20ik ₁

30 =70i ₃ – 50ik ₁ + 20ik ₂ ….. → Vgl 2.

Maar hier hebben we drie (3) variabelen, namelijk i 1, ik 2 en ik 3. En er zijn twee vergelijkingen. We hebben dus ook drie vergelijkingen nodig.

De onafhankelijke huidige bron (in de supermesh ) is gerelateerd aan de veronderstelde maasstromen, d.w.z.

15i x =ik ₃ – ik ₂

i ₃ =15ik x + ik ₂ ….. → Vgl 3.

Vergelijkingen 1, 2 en 3 oplossen met de regel van Cramer of Cramers regelcalculator , Uitschakeling , Gauss-eliminatie of computerondersteund programma zoals MATLAB , vinden we

i ₁ =0,583 A

i ₂ =-6,15 A

i ₃ =2,6 A

We kunnen ook de waarde van V₃ vinden ,

V₃ =ik ₃ x R₃

De waarden plaatsen,

V₃ =2.6A x 40Ω

V₃ =104 V.

Samenvatting van Supermesh-analyse (stap voor stap)

1. Evalueer of het circuit een schaafcircuit is . zo ja, breng Supermesh aan. Zo nee, voer dan een knoopanalyse uit.
2. Teken het circuit opnieuw indien nodig en tel het aantal mazen in het circuit.
3. Label elk van de maasstromen in het circuit . Als vuistregel geldt dat het definiëren van alle maasstromen die met de klok mee moeten stromen, resulteert in een eenvoudigere circuitanalyse.
4. Vorm een ​​supermesh als het circuit stroombronnen van twee mazen bevat . Zodat de supermesh beide mazen zou omsluiten.
5. Schrijf een KVL ( Kirchhoff's Spanningswet) rond elke mesh en supermesh in het circuit . Begin met een eenvoudig en zal één knoop plaatsen. Ga nu verder in de richting van de maasstroom. Neem het "-" teken in het account tijdens het schrijven van KVL-vergelijkingen en het oplossen van het circuit. Er is geen KVL-vergelijking nodig als een stroombron aan de rand van een maas ligt. De maasstroom wordt dus bepaald en geëvalueerd door inspectie.
6. Eén KCL (de huidige wet van Kirchhoff) is nodig voor elke gedefinieerde supermesh en kan worden bereikt door eenvoudige toepassing van KCL. breng in eenvoudige woorden de stroom die van elke stroombron vloeit in verband met maasstromen.
7. Er kan zich een extra geval voordoen als het circuit andere afhankelijke bronnen bevat. Druk in dit geval eventuele aanvullende onbekende waarden en grootheden zoals stromen of spanningen anders dan de maasstromen uit in termen van geschikte maasstromen.
8. Rangschik en organiseer het stelsel vergelijkingen.
9. Los eindelijk het stelsel vergelijkingen voor de knooppuntspanningen op zoals V₁ , V₂ , en V₃ enz. er zal een netwerk van zijn. als je problemen vindt om het stelsel vergelijkingen op te lossen, raadpleeg dan het bovenstaande voorbeeld.

Gerelateerde berichten:

• Thevenin's stelling. Stap voor stap procedure met opgelost voorbeeld
• De stelling van Norton. Eenvoudige stapsgewijze procedure met voorbeeld (beeldweergaven)
• Wet van Ohm:eenvoudige uitleg met verklaring en formules
• Maximale vermogensoverdrachtstelling voor AC- en DC-circuits
• Kirchhoff's stroom- en spanningswet (KCL &KVL) | Opgelost voorbeeld
• Compensatiestelling – Bewijs, uitleg en opgeloste voorbeelden
• Substitutiestelling – Stapsgewijze handleiding met opgelost voorbeeld
• Theorema van Millman - AC- en DC-circuits analyseren - voorbeelden
• Superpositiestelling - Circuitanalyse met opgelost voorbeeld
• Stelling van Tellegen - Opgeloste voorbeelden en MATLAB-simulatie
• Voltage Divider Rule (VDR) - Opgeloste voorbeelden voor R-, L- en C-circuits
• Current Divider Rule (CDR) - Opgeloste voorbeelden voor AC- en DC-circuits
• Star naar Delta &Delta naar Star-conversie. Y-Δ Transformatie