condensatoren en calculus

Condensatoren hebben geen stabiele "weerstand" zoals geleiders. Er is echter een duidelijke wiskundige relatie tussen spanning en stroom voor een condensator, als volgt:

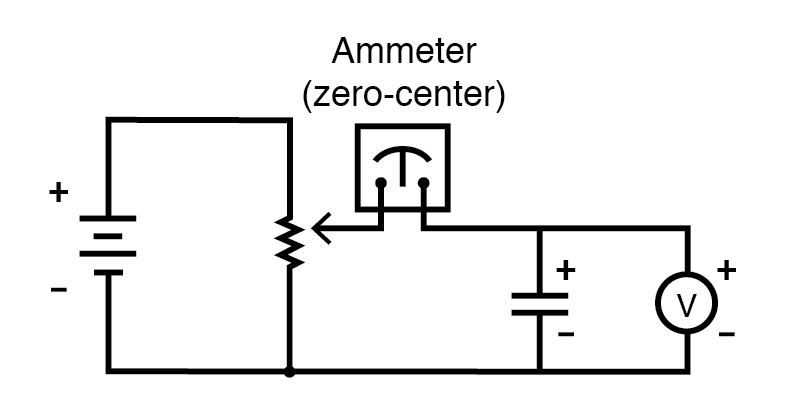
De kleine letter "i" symboliseert onmiddellijk stroom, wat de hoeveelheid stroom op een bepaald moment in de tijd betekent. Dit staat in contrast met een constante stroom of gemiddelde stroom (hoofdletter "I") over een onbepaalde tijdsperiode. De uitdrukking "dv / dt" is ontleend aan calculus, wat betekent dat de onmiddellijke snelheid van spanningsverandering in de tijd, of de snelheid van verandering van spanning (volt per seconde toename of afname) op een specifiek tijdstip, hetzelfde specifieke punt in tijd waarop de momentane stroom wordt verwezen. Om welke reden dan ook, de letter v wordt meestal gebruikt om momentane spanning weer te geven in plaats van de letter e . Het zou echter niet onjuist zijn om in plaats daarvan de momentane spanningsverandering uit te drukken als "de/dt".

In deze vergelijking zien we iets nieuws in onze ervaring tot nu toe met elektrische circuits:de variabele tijd . Bij het relateren van de hoeveelheden spanning, stroom en weerstand aan een weerstand, maakt het niet uit of we te maken hebben met metingen die zijn gedaan over een niet-gespecificeerde tijdsperiode (E=IR; V=IR), of op een specifiek moment in tijd (e=ir; v=ir). Dezelfde basisformule geldt, omdat tijd niet relevant is voor spanning, stroom en weerstand in een component zoals een weerstand.

In een condensator is tijd echter een essentiële variabele, omdat de stroom gerelateerd is aan hoe snel spanning verandert in de tijd. Om dit volledig te begrijpen, kunnen enkele illustraties nodig zijn. Stel dat we een condensator zouden aansluiten op een bron met variabele spanning, gebouwd met een potentiometer en een batterij:

Als het potentiometermechanisme in een enkele positie blijft (wisser staat stil), registreert de voltmeter die over de condensator is aangesloten een constante (onveranderlijke) spanning en registreert de ampèremeter 0 ampère. In dit scenario is de momentane snelheid van spanningsverandering (dv/dt) gelijk aan nul, omdat de spanning niet verandert. De vergelijking vertelt ons dat bij een verandering van 0 volt per seconde voor een dv/dt, er geen momentane stromen (i) moeten zijn. Vanuit een fysiek perspectief, zonder verandering in spanning, is er geen elektronenbeweging nodig om lading toe te voegen of af te trekken van de platen van de condensator, en dus zal er geen stroom zijn.

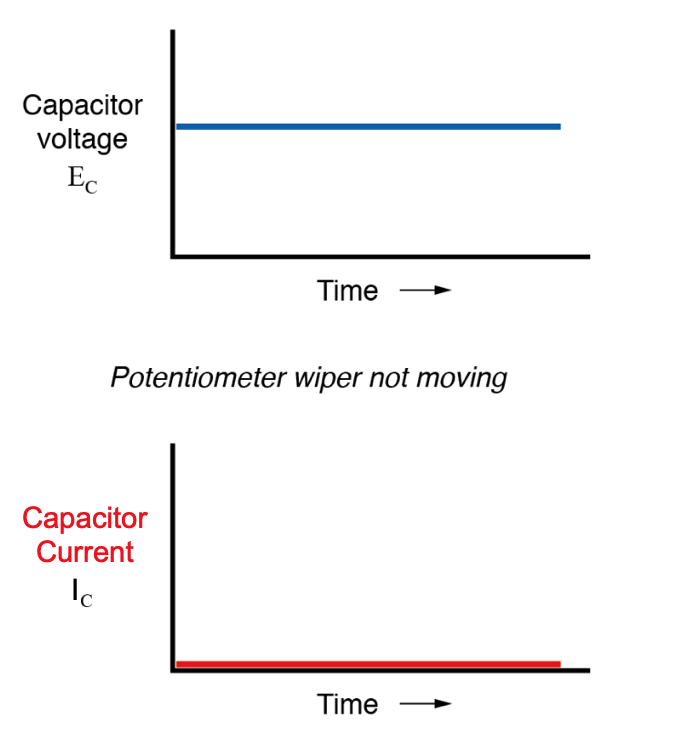
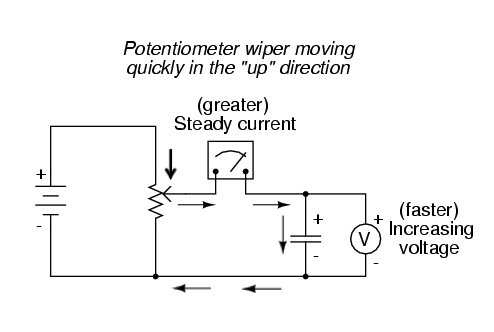
Als de potentiometerwisser nu langzaam en gestaag in de "omhoog" richting wordt bewogen, zal geleidelijk een grotere spanning over de condensator worden aangelegd. De indicatie van de voltmeter zal dus langzaam toenemen:

Als we aannemen dat de potentiometerwisser zo wordt bewogen dat de snelheid Als de spanningstoename over de condensator stabiel is (bijvoorbeeld als de spanning toeneemt met een constante snelheid van 2 volt per seconde), zal de dv/dt-term van de formule een vaste waarde zijn. Volgens de vergelijking resulteert deze vaste waarde van dv/dt, vermenigvuldigd met de capaciteit van de condensator in Farads (ook vast), in een vaste stroom van enige omvang. Vanuit een fysiek perspectief vereist een toenemende spanning over de condensator dat er een toenemend ladingsverschil tussen de platen is. Dus voor een langzame, constante spanningstoename moet er een langzame, constante snelheid van ladingsopbouw in de condensator zijn, wat overeenkomt met een langzame, constante stroomstroom. In dit scenario laadt de condensator op en fungeert hij als een belasting , waarbij stroom de positieve plaat binnenkomt en de negatieve plaat verlaat terwijl de condensator energie ophoopt in een elektrisch veld.

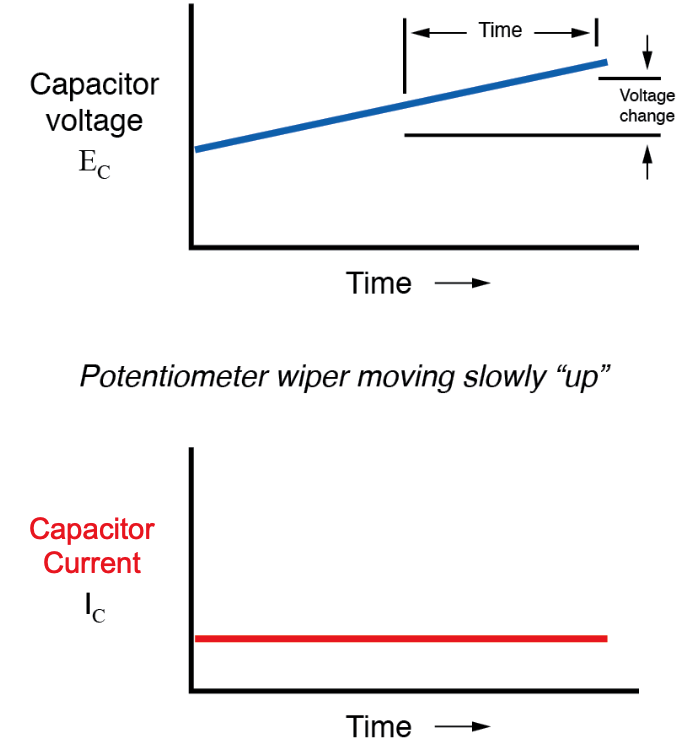
Als de potentiometer in dezelfde richting wordt bewogen, maar met een hogere snelheid, zal de snelheid van de spanningsverandering (dv/dt) groter zijn en dat geldt ook voor de stroom van de condensator:

Wanneer wiskundestudenten voor het eerst calculus bestuderen, beginnen ze met het verkennen van het concept van veranderingssnelheden voor verschillende wiskundige functies. De afgeleide , wat het eerste en meest elementaire calculusprincipe is, is een uitdrukking van de veranderingssnelheid van een variabele in termen van een andere. Calculusstudenten moeten dit principe leren tijdens het bestuderen van abstracte vergelijkingen. Je leert dit principe terwijl je iets bestudeert waarmee je je kunt identificeren:elektrische circuits!

Om deze relatie tussen spanning en stroom in een condensator in calculustermen te zetten, is de stroom door een condensator de afgeleide van de spanning over de condensator in de tijd. Of, in eenvoudiger bewoordingen gesteld, de stroom van een condensator is recht evenredig met hoe snel de spanning erover verandert. In dit circuit waar de condensatorspanning wordt ingesteld door de positie van een draaiknop op een potentiometer, kunnen we zeggen dat de stroom van de condensator recht evenredig is met hoe snel we de knop draaien.

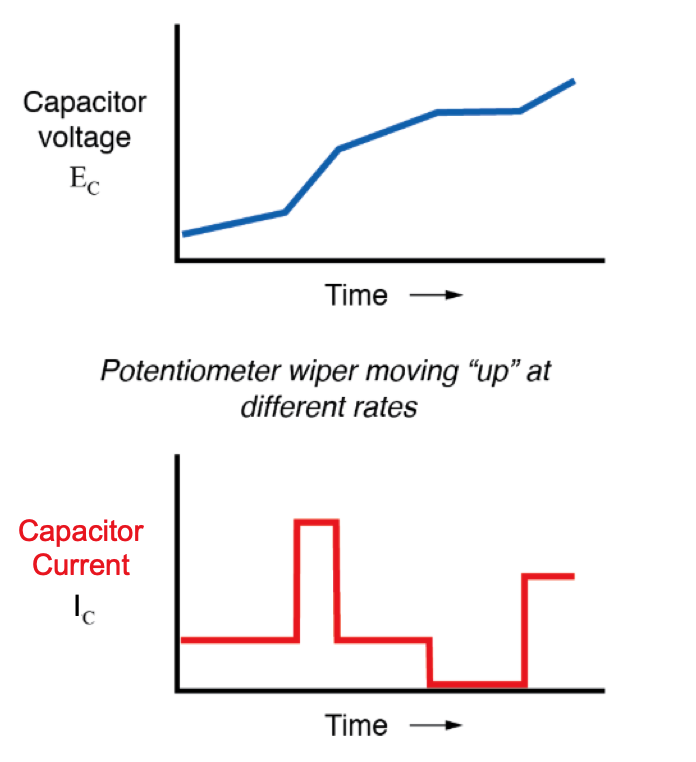
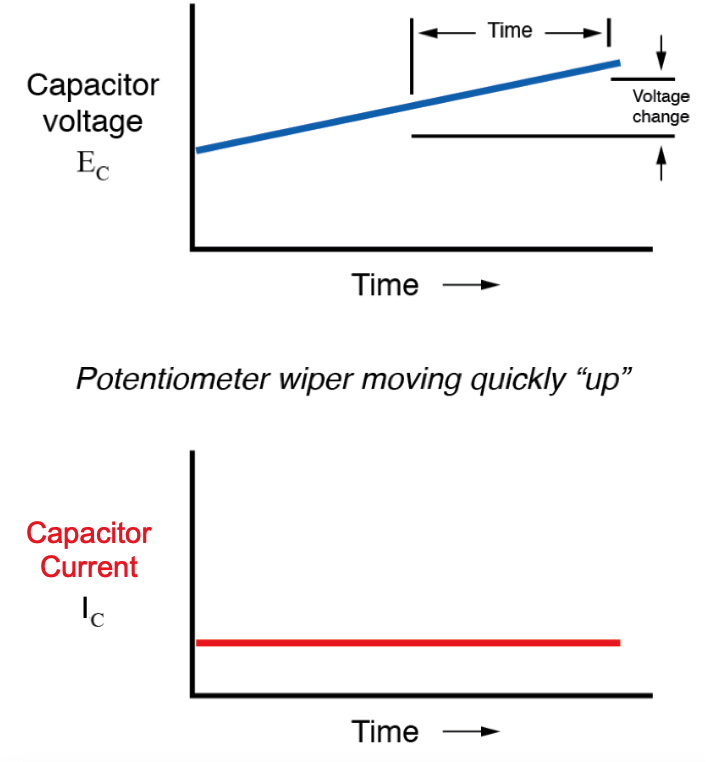
Als we de wisser van de potentiometer in dezelfde richting zouden bewegen als voorheen ("omhoog"), maar met verschillende snelheden, zouden we grafieken krijgen die er als volgt uitzien:

Merk op dat op elk willekeurig moment de stroom van de condensator evenredig is met de veranderingssnelheid, of helling , van de spanningsplot van de condensator. Wanneer de spanningslijn snel stijgt (steile helling), zal de stroom eveneens groot zijn. Waar de spanningsplot een milde helling heeft, is de stroom klein. Op een plaats in de spanningsgrafiek waar deze afvlakt (nulhelling, wat een periode vertegenwoordigt waarin de potentiometer niet bewoog), daalt de stroom naar nul.

Als we de potentiometerwisser in de "neerwaartse" richting zouden bewegen, zou de condensatorspanning afnemen in plaats van te verhogen. Nogmaals, de condensator zal op deze spanningsverandering reageren door een stroom te produceren, maar deze keer zal de stroom in de tegenovergestelde richting zijn. Een afnemende condensatorspanning vereist dat het ladingsverschil tussen de condensatorplaten wordt verminderd, en de enige manier waarop dat kan gebeuren is als de stroomrichting wordt omgekeerd, waarbij de condensator ontlaadt in plaats van wordt opgeladen. In deze ontlaadtoestand, met stroom die uit de positieve plaat komt en de negatieve plaat binnengaat, zal de condensator fungeren als een bron , zoals een batterij, die zijn opgeslagen energie vrijgeeft aan de rest van het circuit.

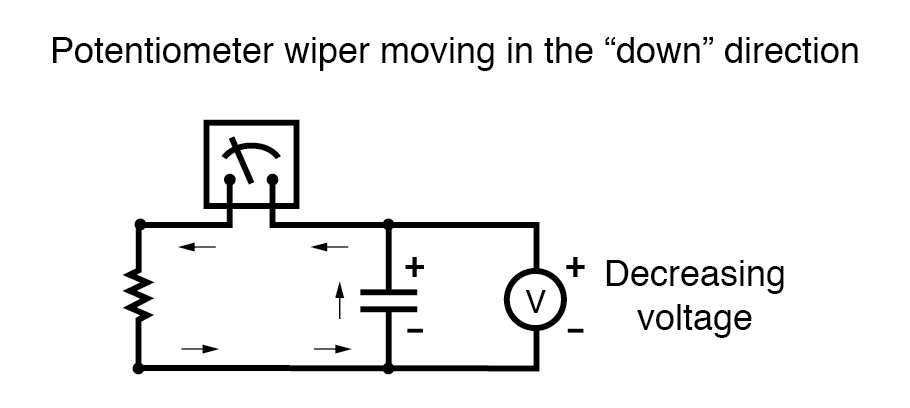
Nogmaals, de hoeveelheid stroom door de condensator is recht evenredig met de snelheid van de spanningsverandering erover. Het enige verschil tussen de effecten van een afname spanning en een toenemende spanning is de richting van de huidige stroom. Voor dezelfde mate van spanningsverandering in de loop van de tijd, hetzij toenemend of afnemend, zal de stroomsterkte (ampère) hetzelfde zijn. Wiskundig wordt een afnemende spanningsverandering uitgedrukt als een negatief dv/dt-hoeveelheid. Door de formule i =C(dv/dt) te volgen, resulteert dit in een stroomgetal (i) dat eveneens negatief is van teken, wat een stroomrichting aangeeft die overeenkomt met de ontlading van de condensator.

GERELATEERDE WERKBLAD:

• Werkblad condensatoren
• Werkblad Berekening voor elektrische circuits